Туннельный безызлучательный перенос протона в молекулах под влиянием флуктуаций классической среды окружения

В рамках квазиклассической теории рассматриваются безызлучательные переходы в молекулах, учитывающие влияние классической полярной среды окружения на процессы туннельного переноса протона. Учтен эффект изменения колебательных частот молекулы при протонном переходе. В случае медленных флуктуаций среды окружения при определенных значениях параметров молекулы получено увеличение скорости туннельного переноса с ростом температуры.

Данная работа была начата летом 1999 г. в сотрудничестве с академиком В. А. Коварским, светлой памяти которого и посвящается.

Теоретические исследования динамики и кинетики процессов переноса протона и атома водорода занимают особое место в химической кинетике. Ввиду значительных квантовых эффектов к ним во многих случаях неприменима теория переходного состояния. Туннельный перенос протона в электронновозбужденном состоянии представляет также фундаментальный интерес в приложениях к биологическим системам.

Недавно выполнен обзор по методам расчета переноса протона [1], поэтому данная задача все еще остается актуальной.

Наше рассмотрение произведем на основе квазиклассического метода, движение протонов описываем классически, а амплитуду перехода по квантовой механике. Такой подход был развит в работах Р. Маркуса. Ограничимся приближением двух протонных термов с близкими значениями энергий. Будем полагать, что соответствующая разность энергий А 21 >>kT, так что вероятности активационных процессов пренебрежимо малы. Существование электрических полей полярной среды окружения может приводить к флуктуациям, при которых эффективная энергетическая щель ∆21 исчезает из-за штарковских смещений уровней и реализуется туннельный безизлучательный переход. Если характерное время изменения флуктуации среды окружения много больше времени туннелирования, то скорость безызлучательного перехода будет возрастать с ростом интенсивности флуктуаций.

В настоящей работе будет принята во внимание более реалистичная модель примесной  молекулы,  учитывающая изменение колебательных частот при протонном переходе, что, как отмечалось в [13-15], может значительно изменить скорость безызлучательного перехода. Полярную среду окружения будем характеризовать гаусс-марковской автокорреляционной функцией ϕ(t1,t2)=B02 exp(-γt1 -t2I).                          (1)

Рис. 1. Кривые 1, 2 соответствуют различным протонным термам молекулы, прямая 3 – отталкивающему терму молекулы, q – точка пересечения, ab – путь туннелирования.

Здесь B 0 - интенсивность шума, зависящая от температуры, у=1/т с . Параметр теории b/k (см. ниже), определяющий температурную зависимость скорости безызлучательного перехода, во многом определяется выбором модели среды окружения. Для низкочастотной классической среды окружения B ₀ ~ Т.

Рассмотрим двухтермовую молекулу, адиабатические потенциалы которой учитывают изменение как положения ядер, так и их колебательных частот в протонных состояниях 1 и 2. Нас будет интересовать туннельный переход системы из состояния 1 в состояние 2 по пути ab (см. рис. 1). Предполагаем, что для колебательных частот в состоянии 1 (ω 1 ) и в состоянии 2 (ω 2 ) выполнено условиеы 1 >>Ы 2 ( П2 1 >>  kT )• Это условие приводит к тому, что низкочастотная полярная среда окружения будет более сильно взаимодействовать с низкочастотным (ω 2 ) молекулярным колебанием в конечном состоянии 2, и для простоты пренебрежем воздействием колебаний среды окружения на колебательную моду с частотой ω 1 в начальном протонном состоянии.

Колебательные гамильтонианы в протонных состояниях 1, 2 имеют вид h2 д

H 1,2     ~    -2 + ^U 1,2 ⁽ q )’

2 m t д q

2 m ω U i ⁽ q ) =       q ^,                                                (2)

U2(q) = m2- q2 - v(q)(q - q)- f(t) q где q - точка пересечения колебательных термов (см. рис. 1), mt – масса осциллятора, m - масса протона, причем mt .>> m.

Сила f(t) представляет собой гаусс-марковский процесс с корреляционной функцией (1). Скорость туннельного безызлучательного процесса может быть представлена в виде (см. «Приложение»)

V ”r

W 21 = T^2Re J d ^{T eX}P^(iE 0 ^T / П ) I 21 ^{( T} ),                (3)

П 0

I 21 ^{( t )} = J dq J ^ф о ⁽ q X^{( K (} q ^т I q^ ф o ⁽ q^         (4)

Здесь     V₁₂

–

2 — 2

80 = (1/2)mrox q ,

матричный элемент перехода   1→2,

E0 = 80+ v(q)V8/x V2/mroi2, ф0(q)-

волновая функция основного состояния осциллятора с частотой ω₁ , К(д^Э – функция Грина, определяемая гамильтонианом Н₂ . Угловыми скобками обозначено усреднение по реализации случайного процесса f(t) . Запишем функцию Грина K( qi lq’) в виде функционального интеграла:

> .

K(qr\ q') = JDq(t) exp< —S(qr\ q') J In

Здесь S(qTlq’) – классическое действие:

T

m

S (qr\q) = J dt —q

0     ²

₂    m ro ^

q2 + (v + f(t))q .

Континуальный интеграл (5) вычисляется по траекториям q(t) , удовлетворяющим граничным условиям q(0)=q’, q(T)=q . Вычисление среднего по реализациям случайного процесса f(t) дает

1 л

i T                        I                   1 i                                                          I expj-Jdt f (t) q (t )h = exp;-H j dt, ddt 2 q (t ^ t,, t 2) q (t 2)^.(6) IpJ0

_ 2 n

0       0

Усредненную функцию Грина ( К ⁽ q r \ q ')} можно записать как

(K(qT \ q')) = J Dq (t) exp pSf(qT \ qf)

> .

Эффективное действие S_e ff (qτ|q’) имеет вид

^T     m     m            iB ^{2 T}

S eff = J ^dt q^q ^- v ^ro 2 q ⁺ vq ⁺ J ^{ds e}xp^{( -} Y \ t ^- s \) q ⁽ t ) q ⁽ s )• ⁽⁸⁾ 0      2       2                2 p 00                                _

Экстремальная траектория q(t) , минимизирующая действие

S eff (qτ|q’) удовлетворяет уравнению

2    iB2 Tv

q + ro2q = —— J ds exp(-y \ t - s |)q(s) + .

pm 0

Эффективное действие на экстремальной траектории (9) имеет вид m1

Seff (qT\ q') =—qq \0 + -vJdtq(t). 22

Континуальный интеграл (7) с экспоненциальной точностью можно записать как [16]

(K(qT\ q')) =

i    a2 s (,cl)

eff

2nx\i dq dq'

1/2

exp

1 sf( qr\q"), n

Отметим, что предэкспоненциальный множитель не зависит от q, q’ , так как экстремальная траектория q(t) есть линейная форма по q, q . Следовательно, выражение (11) для усредненной функции KK ⁽ q ^T \q ')) является точным. Интегродифференциальное уравнение (9) можно привести к дифференциальному уравнению четвертого порядка:

Q ⁽⁴⁾ + ( о 3 - y ² ) Q ⁽²⁾

(2 i y D + y \ o )Q Q = 0,

^Q = q ^- A,

А-    F 0 Y °

A             7 7 ’

2iYD + / ®2

B 0 D = -⁰-,

П m

F 0 = v • m

Две дополнительные константы интегрирования определяем из уравнения (9) в точках t=0, t=T . Подставляя (11) в выражение для производящей функции (4) и вычисляя элементарные гауссовские интегралы по q, q ’ , находим I 21 (t) ; затем по формуле (3) определим скорость безызлучательного перехода. Решение граничной задачи (9), (12) очень громоздко. Рассмотрим поэтому предельные случаи медленных флуктуаций среды окружения.

В пределе медленных флуктуаций среды окружения ( k<<1, b/k>>1 ) экстремальная траектория имеет вид

q ( t ) = q Z qt + q + 1 F o ^{+ (1/2)} D ^{( q + q ) т} ( t, - t T ). т 2    1 + ( D t ³/12)

Используя (10), (11), (15), получим следующее выражение для производящей функции в случае медленных флуктуаций среды окружения:

1 21 ( X ) =

V1 - ibx

V1 + ix /2 ^1 + ( bx ² / 2)(1 + ix / 6)

x exp

-

1 + ix /6

1 + ( bx ² / 2)(1 + ix /6)

•

Здесь x = 60 1 т ,   V 0 = v ² /h т а\ . В случае медленных флуктуаций,

2              > при значениях параметров   V0 << 1, А21 ро общее выражение (3) для скорости безызлучательного туннельного перехода может быть преобразовано для достаточно широкого потенциального барьера к виду

W 21 = W 2⁽1⁰⁾ exp(^{2 B} ₂ ⁰ ξ ² ),                                     (25)

V ₀

W ₂ ⁽ ₁ ⁰⁾ - константа, не зависящая от температуры, есть скорость процесса в отсутствии внешней среды окружения и сводится к выражению

3/2

W ₂ ⁰ ₁ = ϖ      exp( - 2 s ₀ )exp( - ), s ₀ = ⁰            (26)

s ₀                   3 v h ω 1

Здесь ϖ - частота скорости перехода. А для ξ получаем выражение 3/2

ξ = ^{1 ε 0} - ^{ε 0} (2 - 1) .

3 V ₀    h ω ₁

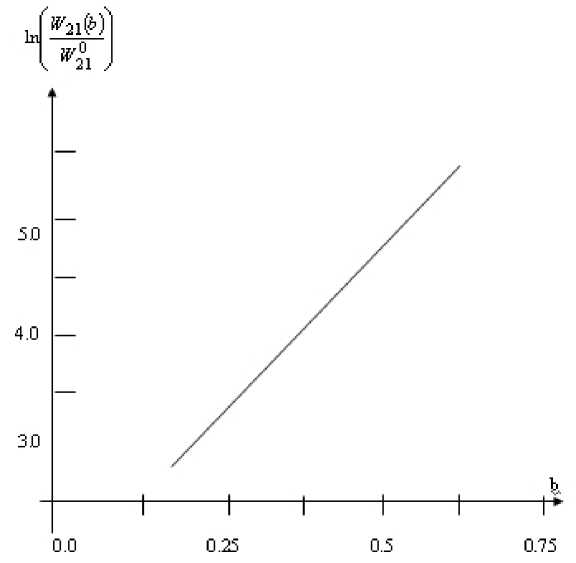
Рис.2. Зависимость вероятности туннельного безизлучательного перехода от параметра b

( W ₂ ⁰ ₁ - вероятность туннельного перехода в отсутствие среды, W ₂ ⁽ ₁ ⁰⁾ = W ₂₁ (b=0 ) = 0.0096 × 10 ^{- 11} ).

Температурная зависимость скорости перехода определяется выражением (26). На рис. 2 приведена зависимость вероятности туннельного перехода от параметра b , при фиксированном значении остальных параметров. В модели среды окружения, где ( b ^ Т), из рис. 2 видно, что скорость безызлучательного перехода увеличивается с интенсивностью флуктуаций и ростом температуры.

Приведенный выше анализ температурной зависимости скоростей туннельного перехода протонно-колебательной системы при низких температурах показывает, что полярная среда окружения > с частотами (v(nv kT) существенно влияет на скорость безызлучательного перехода. В случае медленных флуктуаций среды окружения при определенном выборе параметров системы получается увеличение скорости перехода с ростом температуры.

Приложение

Матрица плотности рассматриваемой системы определяется уравнением

ih p = [H, p], H = H0 + V , где Hi и H2 колебательные

гамильтонианы основного 1 и

конечного 2 электронно-колебательных состояний,

V

это

оператор , обуславливающий

перенос протона, а

V 12

- матричный

элемент оператора возмущения (например оператор спин-орбитального взаимодействия или матричный элемент коэффициента функции электронного взаимодействия с промотирующей модой). Этот матричный элемент не зависит от переменных акцептирующей моды. Вопрос об операторе возмущения решается с учетом возможных правил отбора и могут происходит переходы с оборачиванием спина.

В уравнении П1 для матрицы плотности перейдем к представлению взаимодействия a = S+pS , ih S = H0S,

S(t,t) = 1, S(t,t')S(t',t0) = S(t,10).(П2)

Матричные элементы  O21  матрицы a определяются вероятностями квантовых переходов и удовлетворяют уравнению

.        ~                   ~~ ih a21 = V 21 a11 - a22 V 21, V 21 = S2 S1V12.(П3)

Оператор эволюциии

^ 1,2 определяется гамильтонианами

H 1,

2 . Предположим что возмущение, обуславливающее переход мало, и под его влиянием заселенности в слагаемых 1 и 2 изменяются мало от величин в отсутствии возмущений , то есть остаются равновесными

11 ~ Р и = Z ^{- 1 ex}P⁽

^H )

kT ,

Z = Sp(exp(- H1) .

kT

Вероятности переходов из состояния 1 в 2 определяются выражением

W 12 <<  ^Р 22 >>  •

Внутренние угловые скобки обозначают усреднения по колебательным параметрам слагаемого 1. Внешние угловые скобки определяют усреднение по реализациям случайной силы f ( t ) .

Далее находим искомую вероятность

² Wn = ^ V T ¹²    h²

Re ^dt << S2(t, t') S1(t\ t) >>, t 0

где 10 - момент переключения взаимодействия , t — 10 —^ ^ , из чего мы и получаем формулу (3).