Турбулентность в канале акустического анемометра

На кафедре ЭИС в МГГУ был разработан акустический анемометр. В основе его принципа действия лежит фазово-акустический метод [1]. Датчик анемометра представляет собой цилиндрический волновод-воздуховод, в стенки которого вмонтированы кольцевые пьезопреобразователи. Электрический сигнал поступает на излучающий преобразователь, а с приемного преобразователя снимается сигнал, являющийся результатом аэроакустического взаимодействия в волноводе. Измеряется разность времени прихода одной и той же фазы сигналов распространяющихся по и против потока. Преобразователи являются попеременно то излучателем, то приемником. Анемометр работает в диапазоне скоростей от 0,1 до 30,0 м/с. Абсолютная погрешность его измерения вычисляется по формуле 5 V = 0,02 + 0,02 V .

Число или критерий Рейнольдса (Re) — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье-Стокса [3]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса определяется следующим соотношением:

pvL  vLQL

Re = —= —= ^j, где(1)

П   V

ρ — плотность среды;

v — характерная скорость;

L — характерный размер;

η — динамическая вязкость среды;

Q — объёмная скорость потока;

A — площадь сечения трубы.

Для каждого вида течения существует критическое число Рейнольдса, Recr, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При Re < Recr течение происходит в ламинарном режиме, при Re > Recr возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения воды в круглой трубе Re ≈ 2300 .

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков.

ρ = 1.293( кг / м ³) - плотность воздуха

D = 28 ⋅ 10 ^{- 3} - диаметр трубы

µ = 17.2 ⋅ 10 ^{- 6}- коэффициент динамической вязкости воздуха

Число Рейнольдса найдем из формулы:

ρ ⋅ V ⋅ D

Re =        , причем скорость V возьмем в диапазоне от 0 до 30 м/с

µ с шагом в 0.2 м/c.

Полученный результат изображен на рис. 1.

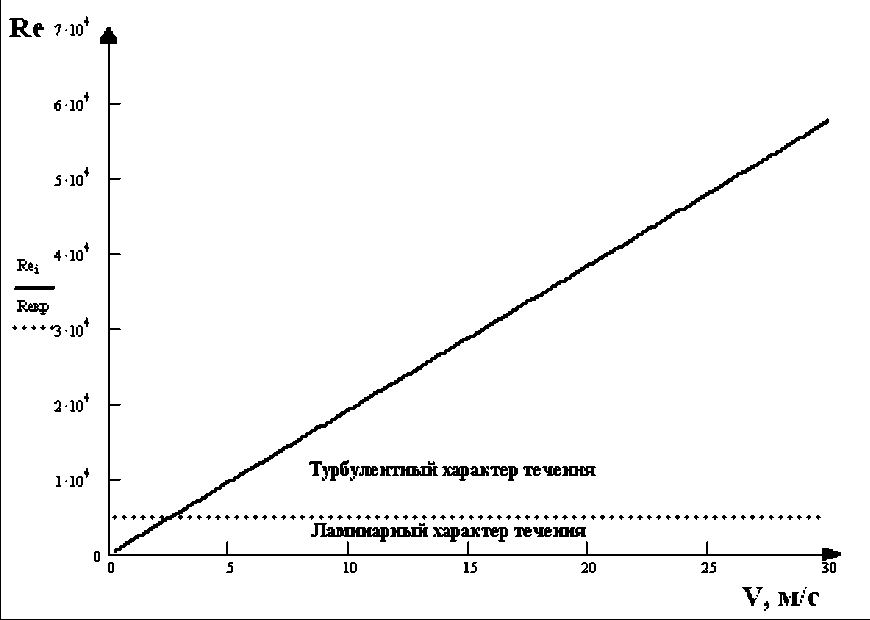
Рис. 1. Расчетные значения числа Рейнольдса для диапазона скоростей от 0 до 30 м/c

Критическое значение числа Рейнольдса для течения в круглой трубе возьмем равным 5·103 (изображен на графике красной прерывистой линией).

Из проведенных вычислений видно, что на большей части диапазона измерений (начиная со скорости 2,6 м/с) течение в трубе является турбулентным. Следовательно, характер течения оказывает влияние как на среднюю скорость течения потока, так и на различие скоростей между слоями течения, особенно в пристеночном (пограничном) слое. Для выяснения влияния турбулентных пульсаций в воздуховоде акустического анемометра на скоростях свыше 2,6 м/с необходимо проведение дополнительных исследований с помощью специального оборудования (сверхточные игольчатые анемометры или анемометрические иглы).

Рассмотрим выходные данные, полученные из статьи [2]. На рис. 2 изображен спектр турбулентных пульсаций для различных скоростей потока.

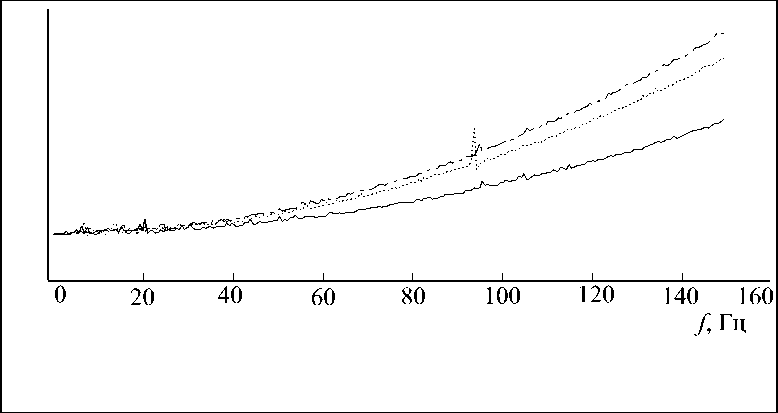
Рис. 2. Спектральная плотность мощности на входе акустического анемометра при средней скорости потока равной

0 м/с

5,6 м/с

7,0 м/с

Можно констатировать, что отсутствие пиков на частотах, кратных частоте напряжения питания, при наличии потока говорит о том, что вклад турбулентности в случайный процесс измерения скорости потока значительно превышает вклад погрешности анемометра и является основным. Рассчитанные Рейнольдсовы напряжения подтверждают преобладание характера турбулентного течения на большем диапазоне измерения скоростей акустического анемометра. Для выявления влияния скоростей акустического анемометра на среднюю скорость движения потока необходимо продолжение исследований с использованием специализированного      оборудования      (высокочувствительных анемометрических игл).

Литературы

• 1.    Шкундин С.З. Лашин В.Б. Метрология. 1990 г.

• 2.    Шкундин С.З., Буянов С.И., Румянцева В.А. Спектральный анализ пульсаций скоростей потока, измеренных акустическим анемометром / Измерительная техника, 2004, №4, с.46-48.

• 3.    Шлихтинг Г., Теория пограничного слоя. – М.: Наука, 1974.