ТВЕРДОТЕЛЬНЫЙ ЛАЗЕР ДЛЯ НАУЧНЫХ ИССЛЕДОВАНИЙ С КОРРЕКЦИЕЙ ТЕПЛОВОЙ ЛИНЗЫ В РЕЗОНАТОРЕ. II. МЕТОДИКА И РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ

Целью численной оптимизации резонатора, оптическая схема которого показана в части 1 настоящей работы [1], являлось определение параметров корректирующих элементов резонатора: фокусов линз Л1 и Л2 и расстояния между ними ( F 1 , F 2 и L 1 ), которые обеспечивали бы устойчивую генерацию на низшей (гауссовой) моде при максимальной мощности излучения в условиях, когда заданы световые апертуры активной среды (квантрон GN-50) и блока модуляции потерь в резонаторе (диафрагма Д2). Оптимизация проводилась в рамках метода расчета резонаторов на основе АВСD -матриц. Этот метод позволяет оценить радиус сечения гауссова пучка, являющегося собственной функцией (модой) резонатора (т.е. воспроизводящейся на каждом проходе по резонатору). Задача оптимизации состояла в определении такого набора варьируемых параметров резонатора, при котором потери низшей моды на диафрагме Д2 были бы достаточно малы, в то время как высшие поперечные моды эффективно "отфильтровывались" бы этой диафрагмой.

Оптимальный радиус пучка wo, удовлетворяющий этому условию, может быть реализован при достаточно большом числе сочетаний параметров резонатора. Преимуществом будет обладать та схема резонатора, мода которой наиболее полно заполняет активную среду и обеспечивает максимальный съем энергии накачки. В связи с этим при численной оптимизации в качестве критерия качества принимались значения радиусов сечений гауссовых пучков резонаторной моды wo и wac в плоскостях диафрагмы Д2 и активной среды.

МЕТОДИКА ПРОВЕДЕНИЯ РАСЧЕТОВ

Эквивалентная схема резонатора для проведения расчетов показана на рис. 1.

При оценке параметров гауссова пучка в резонаторе на основе метода АВСD -матрицы вводят комплексный параметр пучка q [2], связанный с радиусом сечения пучка w по уровню e^–1 интенсивности соотношением:

11 i — +    2 .

q R kw ²

Комплексный параметр пучка q при распространении по резонатору, содержащему участки свободного пространства и квадратичные фазовые корректоры (линзы, зеркала), изменяется в соответствии с выражением:

Aq + B q + i ^— 77"    ,

Cqi ⁺ D

где A , B , C и D — элементы ABCD- матрицы резонатора.

ABCD- матрица распространения на расстояние L в свободном пространстве имеет вид:

T —

1 L

0 1,

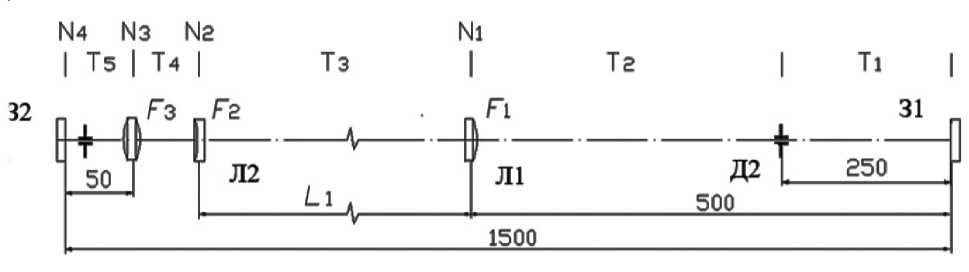
Рис. 1. Эквивалентная схема резонатора для расчетов

F ₁, F ₂, F ₃ — фокусные расстояния корректирующих линз и тепловой линзы активной среды; L ₁ — расстояние между линзами Л1 и Л2; T 1 –T 5 и N 1 –N 4 — обозначения матриц свободного пространства и квадратичных фазовых корректоров соответственно; З1, З2 — плоские зеркала

а при прохождении линзы или зеркала:

N =

- 1 F

где F — фокусное расстояние, которое считается положительным для положительных линз и вогнутых зеркал. Любая сложная оптическая система может быть описана ABCD- матрицей, которая получается путем перемножения ее составных частей.

На рис. 1 представлена эквивалентная оптическая схема рассматриваемого резонатора, разбитая на отдельные элементарные отрезки, описываемые ABCD- матрицами типа T и N. При этом ABCD- матрица полного обхода излучения по резонатору (от диафрагмы Д2 к зеркалу 1 (З1), затем обратно к зеркалу 2 (З2) и диафрагме Д2) будет иметь следующий вид:

T i - T i - T 2 - N i - T 3 - N 2 - T 4 - N 3 - T 5 - T 5 - N 3 - T 4 - N 2 - T 3 - N i - T 2 .

Здесь N 3 — матрица эквивалентной тепловой линзы квантрона, остальные обозначения АВСD -матриц ясны из рисунка.

Гауссов пучок будет являться модой резонатора (т.е. будет воспроизводиться с точностью до константы после полного обхода по резонатору) при условии выполнения равенства

Aq + B q = —----. Решение данного уравнения можно

Cq + D записать в виде

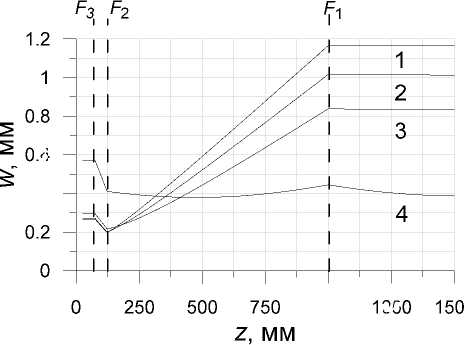
Рис. 2. Зависимости радиуса w сечения гауссова пучка в резонаторе от продольной координаты z.

При фокусных расстояниях F 2 : 1 — 90, 2 — 100, 3 — 110 и 4 — 130 мм; F 3 = 170 мм; F 1 = 1000 мм; L 1 = 870 мм

kw 2 =

2 B .

74 - ( A + D )² ’

На основании решения (2), используя выражение (1), легко получить параметры гауссова пучка в любой плоскости резонатора. Для примера на рис. 2 приведены результаты расчетов в виде зависимости радиуса сечения w гауссова пучка в резонаторе от продольной координаты z при различных значениях F 2 . Пунктирными линиями на рисунке показаны положения линз с фокусами F 1 , F 2 и тепловой линзы с фокусом F 3 .

На рис. 3 представлена диаграмма устойчивости резонатора (область реальных значений w o ), полученная на основании решения (2). Серия кривых на рис. 3, а, соответствует радиусам сечения гауссова пучка w o в области диафрагмы Д2, а на рис. 3, б, — радиусам сечения пучка w ac в области

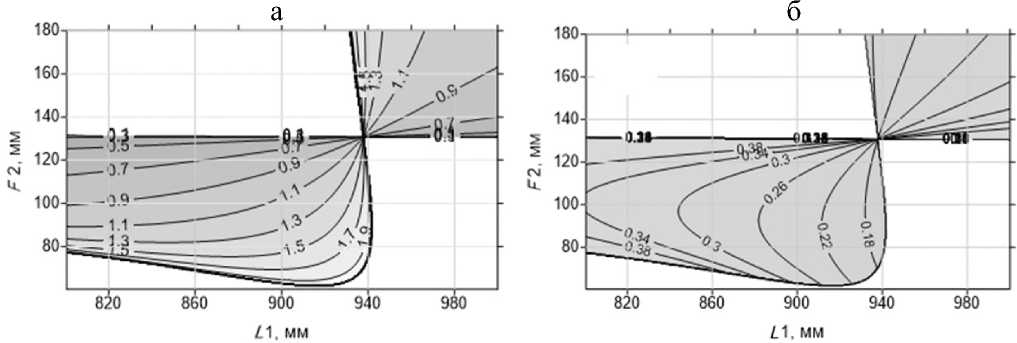
Рис. 3. Диаграмма устойчивости резонатора, построенная в координатах ( F 2 , L 1 )

активной среды, полученным для различных значений фокуса корректирующей линзы F 2 и ее различных положений в резонаторе.

Как видно из представленных на рис. 2 и 3 графиков, сечение пучка в резонаторе может существенно меняться как на апертурной диафрагме Д2, так и в области активной среды.

Предложенная расчетная методика позволяет сформировать такие значения параметров F 1 , F 2 и L 1 , для которых низшая поперечная мода резонатора (значения w о и w ас ) наилучшим образом заполняла бы активную среду и имела низкие потери на диафрагме Д2. Следует, однако, отметить, что анализ, проведенный в рамках аппарата ABCD- матриц, выполняется в приближении гауссовой низшей моды устойчивого резонатора. Строго говоря, это приближение верно только для резонаторов с "гауссовыми" зеркалами [3] либо в случае, когда диаметр жестких диафрагм в резонаторе заметно превышает размер сечения низшей моды и дифракционные потери оказываются незначительными. Поэтому на практике оказывается чрезвычайно важным вопрос соотношения между размерами апертурных диафрагм в резонаторе и оптимальным размером низшей гауссовой моды, при котором реализуется одномодовый режим с максимальной мощностью генерации.

Для анализа этого соотношения использовался волновой подход описания мод резонатора. Расчеты, учитывающие дифракционные эффекты, проводились на основе широко используемой в литературе методики расщепления по процессам дифракции и усиления-рефракции при решении задачи Коши нахождения собственных функций заполненного активной средой резонатора [4]:

= [ g ( x, У , ^z ) ⁺ Y i ( x , У , ^z ) ] E ±               ⁽³⁾

с граничными условиями E - ( L ) = r m E ₊ ( L ), E ₊ (0) = E - (0), где E ( x,y,z ) — комплексное световое поле, связанное с интенсивностью света выражением I ( x , y , z ) = E ( x , y , z )| 2 . Здесь k = 2 n / X₀ , X₀ — длина волны излучения, а g ( x , y , z ) и γ i ( x , y , z ) — коэффициент усиления и пассивные потери в резонаторе.

Коэффициент усиления рассчитывался на основе кинетических уравнений:

N_K + N 2 = N t ,

N 2

= W p N g

— BqN 2

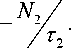
Здесь N g и N 2 — населенности нижнего и верхнего лазерного уровней соответственно, W p — мощность накачки, q — коэффициент усиления, B — сечение лазерного перехода, τ 2 — время жизни возбужденного состояния, N t , — концентрация ионов Nd⁺³.

Расчет излучения в резонаторе проводился итерационным способом: после расчета светового поля пересчитывался коэффициент усиления активной среды, соответствующий распределению интенсивности света в активной среде, затем происходил переход на новый шаг по времени. При достаточно высокой селекции мод по потерям (определяемым размерами ограничивающих диафрагм) итерационный процесс устанавливался к низшей поперечной моде. В противном случае

dE+   । d    d |

2i k   ± + <--1--> E± dz   [dx dy

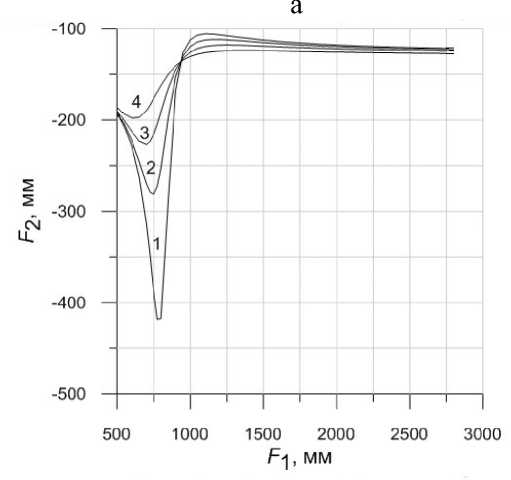
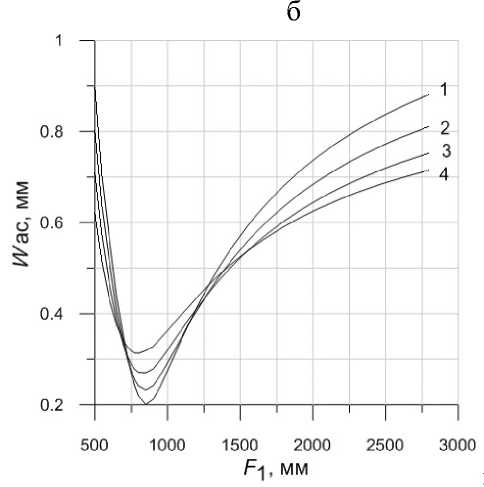
Рис. 4. Результаты решения уравнения (2) при w _o = 0.9 (1), 0.8 (2), 0.7 (3) и 0.6 мм (4)

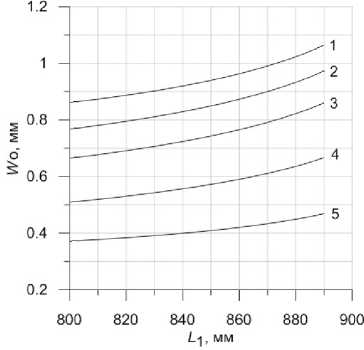
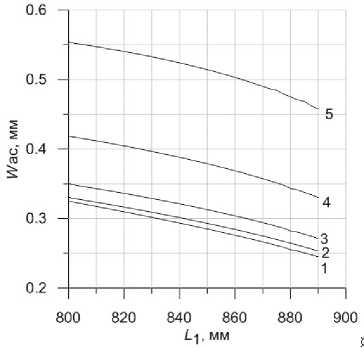
Рис. 5. Зависимость радиуса сечения пучка в плоскости диафрагмы Д2 (a) и активной среды (б) от положения линзы Л2 в резонаторе для F ₂ = = 105 (1), 112 (2), 120 (3), 130 (4) и 135 мм (5)

а

б

наблюдался режим биения мод, соответствующий многомодовому режиму генерации.

Результаты расчета лазерной моды при различных соотношениях w _o и диаметра апертурных диафрагм в резонаторе приведены в следующем разделе.

РЕЗУЛЬТАТЫ ЧИСЛЕННОЙ ОПТИМИЗАЦИИ

Для решения задачи оптимизации выражение (2) рассматривалось как уравнение относительно неизвестных параметров резонатора (F1, F2 и L1), а значение wo использовалось как параметр этого уравнения. Результаты решения уравнения (2) представлены на рис. 4, где для нескольких фиксированных значений размера пучка wo приведены зависимости фокусного расстояния корректирующей линзы Л2 (а) и радиуса сечения пучка в активной среде wac (б) при различных значениях фокусного расстояния линзы Л1. Расчеты проведены для L1 = 870 мм и фокусного расстояния тепловой линзы F3 = 170 мм, соответствующей току накачки порядка 20 А [1].

Из представленных графиков видно, что для размеров сечения пучка w o от 0.6 до 0.9 мм ("соответствующих" диаметру диафрагмы Д2 D =

= 2.5 мм) фокусное расстояние отрицательной линзы Л2 следует выбирать в области от –100 до –130 мм при фокусном расстоянии линзы Л1 в области 1100–1200 мм. При этом радиус пучка в активной среде w ac составляет 0.4–0.5 мм.

При выборе параметров резонатора важным является вопрос о возможных отклонениях реальных значений оптимизируемых параметров резонатора от номинальных значений. На рис. 5 представлены графики, демонстрирующие зависимости радиусов пучка в резонаторе от смещения корректирующей линзы Л2 относительно положения L 1 = 870 мм, принятого на рис. 4. Зависимости получены для нескольких фиксированных значений F ₂ вблизи области оптимальных значений. Как видно, при продольном смещении линзы на 20 мм сечения пучка могут меняться в пределах от 10 до 20%.

Приведенные выше результаты оптимизации резонатора получены для фиксированного значения фокусного расстояния тепловой линзы F3 = = 170 мм, соответствующей току накачки порядка 20 А. В связи с этим представляет интерес оценка чувствительности моды резонатора к изменению тока накачки. На рис. 6 приведены графики изме- нения радиусов сечения пучка в резонаторе при варьировании оптической силы тепловой линзы F3, характеризующие данную зависимость.

Из представленных данных видно, что в зависимости от оптической силы линзы, наведенной в активной среде, при изменении тока накачки от 18 до 20 А [1] сечение гауссова пучка в резонаторе меняется существенным образом, что неизбежно будет сказываться на устойчивости генерации. В этих условиях стабилизировать характеристики излучения лазера возможно путем продольного смещения линзы Л2 в оптимальное положение для текущего тока накачки (см. также рис. 5).

Таким образом, расчеты, проведенные в приближении квазигеометрической оптики, позволили получить параметры резонатора ( F 1 , F 2 и L 1 ), обеспечивающие размеры низшей моды w o , близкие к диаметру апертурной диафрагмы Д2. Для окончательного выбора оптимального значения w o проводились дифракционные расчеты (по описанной выше методике) с параметрами резонатора, полученными в ходе квазигеометрической оптимизации.

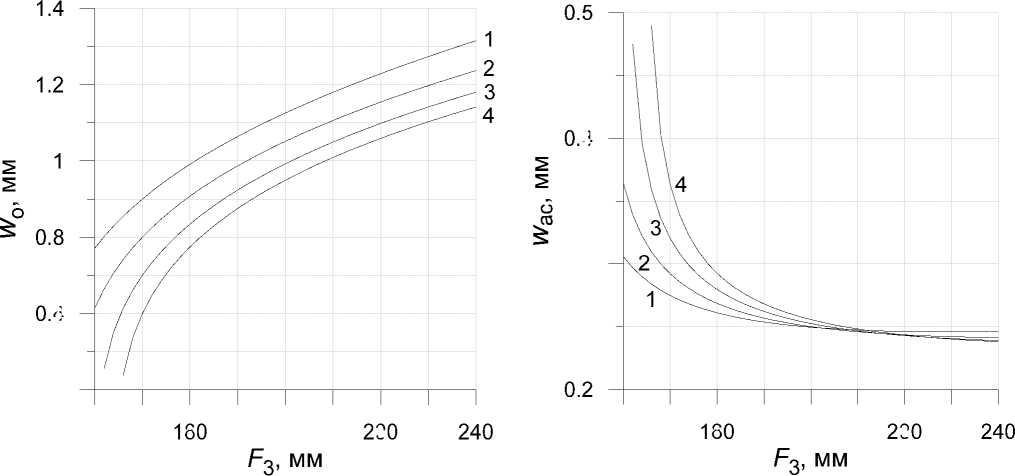
Рис. 6. Зависимость радиуса пучка на диафрагме Д2 (a) и в активной среде (б) от фокусного расстояния тепловой линзы F ₃ при F ₂ = 112 (1), 119 (2), 125 (3) и 130 мм (4); L ₁=870 мм, F ₁=1000 мм

y, мм                                          y, мм

0.25

0.2

0.15

0.1

0.05

О

■0.05

-0.1

0.15

-0.2

■0.25

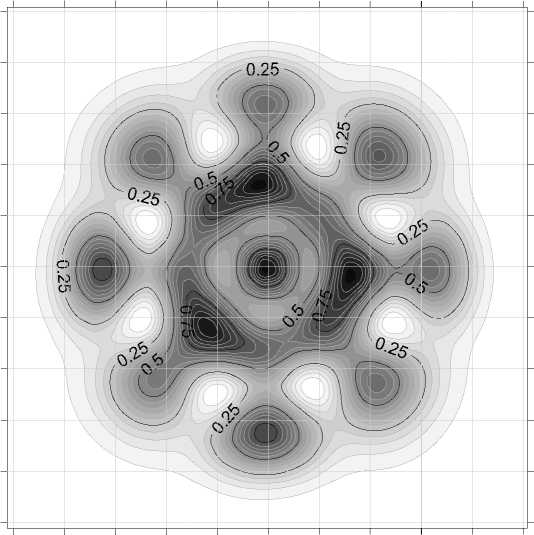
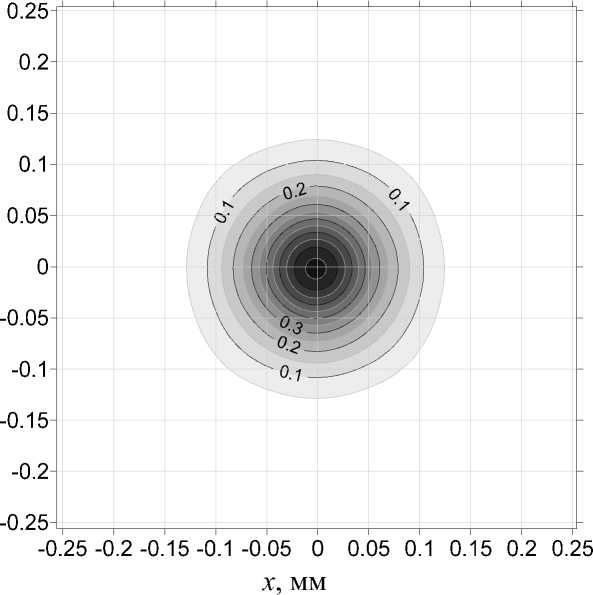
Рис. 7. Распределение интенсивности пучка на диафрагме Д2.

Диаметр диафрагмы: а — D = 2.5, б — D = 5 мм

б

• -0.25 -0.2 -0.15 -0.1 -0.05 0 0.05 0.1 0.15 0.2 0.25

x, мм

Пример результатов дифракционного расчета представлен на рис. 7, где изображены пространственные структуры излучения в резонаторе, соответствующие стационарной гауссовой моде "работающего" в одномодовом режиме резонатора (а) и одному из мгновенных пространственных распределений интенсивности излучения, представляющему собой суперпозицию высших поперечных мод резонатора при многомодовой генерации (б). Расчет выполнен для комплекса параметров, выбранных выше: F 1 = 1000 мм, F 2 = –125 мм ( w o = 0.7 мм), F 3 = 170 мм, L 1 = 870 мм.

Результаты расчета зависимости мощности генерации от диаметра диафрагмы Д2 для четырех рассматриваемых значений радиусов пучка w o приведены на рис. 8. Как и следовало ожидать, с увеличением апертуры резонатора растет мощность выходного излучения. Причем нарастание мощности происходит неравномерно, что связано с изменением числа Френеля резонатора для каждого значения D и варьированием условий интерференции волн, распространяющихся в резонаторе. Насыщение прироста мощности наблюдается, когда пучок при увеличении D начинает виньетироваться не диафрагмой Д2, а апертурой активной среды (см. кривые 1 и 2).

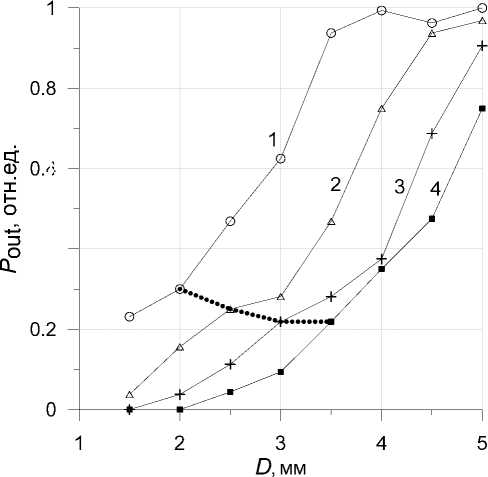
Рис. 8. Зависимость мощности излучения от диаметра диафрагмы Д2 при различных параметрах резонатора, соответствующих w o = 0.6 (1), 0.7 (2), 0.8 (3) и 0.9 мм (4)

На рисунке пунктирной кривой отмечена граница перехода генерации из одномодового в многомодовый режим. Как видно, небольшой выигрыш в максимальной мощности генерации, которую можно достичь в одномодовом режиме, имеет резонатор, сконфигурированный под радиус сечения моды w o = 0.6 мм. Однако, как показал расчет, такой резонатор более чувствителен к флуктуациям оптической силы термолинзы, и генерация в этом случае может быть менее устойчива по сравнению с другими вариантами параметров.

Необходимо отметить, что все точки на пунктирной кривой, ограничивающей область одномодовой генерации, c хорошей точностью удовлетворяют соотношению

D ≈ 3.5 ⋅ w ₀, (5) которое связывает размеры гауссова пучка, генерируемого в резонаторе, с диаметром ограничивающей диафрамы Д2.

ВЫВОДЫ

В заключение отметим, что для расчета параметров резонатора твердотельного лазера с длиной до 1.5 м, работающего в режиме одной поперечной моды с близкой к дифракционной угловой расходимостью пучка и максимальной мощностью генерации, необходимо придерживаться следующей методики.

Активная среда квантрона располагается вблизи глухого плоского зеркала резонатора, в состав резонатора дополнительно вводятся две компенсирующие линзы: отрицательная, располагаемая вблизи квантрона, и положительная, располагаемая на расстоянии L 1 от нее.

Проводится оценка фокусного расстояния F 3 тепловой линзы, наведенной в применяемом кван-троне при заданном токе диодной накачки.

Для заданной апертуры выходного пучка лазера (диаметра апертурной диафрагмы D ) на основе выражения (5) определяется необходимый размер сечения гауссова пучка w o в плоскости диафрагмы. Затем на основании полученного значения w o и оценок оптической силы тепловой линзы F 3 по приведенной выше методике рассчитываются фокусные расстояния F ₁ и F ₂ и положение корректирующих линз в резонаторе.

Работа выполнена при финансовой поддержке Минобрнауки РФ в рамках государственного задания № 075-00913-21-01 "Методы управления параметрами излучения твердотельного лазера с помощью переключаемого интерферометра Майкельсона".