Two-level genetic algorithm for X-ray powder diffraction structure analysis

Crystal structure information is essential for explanation and prediction of physical and chemical properties of investigated materials. Many materials, multi-phase mixtures in particular, are available in form of powder only, thus severely impeding a research. In such cases X-ray powder diffraction methods, which are being intensively developed during last two decades, are used. They are based on analysis of a whole X-ray diffraction profile of powder pattern, which is a monochromatic X-ray radiation intensity function of polycrystalline sample diffraction angle. By now, in general, crystal cell parameters search problem (indexing methods) and structure model refinement problem (Rietveld method) have been solved. Primary mathematical means used for these problem solutions is a non-linear least-squares method (LSM). Plausible structure model determination in case of powder samples is still a problem even in case of relatively simple structures [1].

In recent years, for this problem solving so-called “directspace” methods [1] have become of use. They are based on probabilistic generation of trial crystal structure models, their assessment through weighted difference of calculated and observed patterns (profile R-factor) and search for global minimum over corresponding parametric hypersurface in order to find an adequate structure model. An example of this approach is evolutionary algorithm, mimicking processes of natural selection in search of an optimal structure solution [2]. Several implementations of this concept have already been used for structure determination, demonstrating promising prospects [1; 3]. Here a two-level hybrid genetic algorithm is suggested for that purpose and its approval results are described on real patterns of single- and multi-phase polycrystalline samples with well-known crystal structure.

Full-profile crystal structure model refinement. As a tool for crystal structure model refining multi-phase Rietveld method [4] was used. An essence of Rietveld method is a modeling of experimental pattern by complex multi-parametric function:

Y ^mod( P , O j ) =

n

• = Z Q , ( P l , O j )* I^( P s , O j ) + B ( P _B , O j ), (1)

where 0 j - diffraction angle; Q , - profile functions for diffraction lines i , dependent on profile parameters set _L , (positions, half-width, form, asymmetry of lines, etc.); I_i ^calc – calculated integral intensities of lines, dependent on structure parameters set P _S (atomic coordinates, thermal motion parameters, etc.); В - function for background, dependent on background profile parameters set P _B .

Firstly, pattern model is calculated from the approximate (initial) values of parameters P , including model atomic coordinates in crystal cell. Exact coordinates and other parameters (including quantitative phase composition in case ofmulti-phasesample) aredeterminedasaresultofmathematical fitting of model pattern to observed pattern by structure and profile parameters least-squares method variation.

Formalizing the approach, we get a following mathematical optimization problem. Experimental data (powder pattern) represent a discrete sequence { _j, Y_j } of size m , sorted by ascending of _j. Some class of parametric function Y ( P , ) (Rietveld method functions) is given, P is a set of profile and structural parameters (a vector of size N ), 6 - independent argument. Peculiarities of the problem are large dimensionality (can exceed 100 parameters) and nonpolynomiality of functions.

With a given distribution of observed values of function Y ^obs( )= { _j , Y_j } and initial parameters approximation P ₀ the task is to find function Y ^mod of class Y^. ( P , ) and an optimal set of parameters * to satisfy condition (2).

LSM functional:

Ф ( P ) = £ ( у ^mod( p , 9 j ) - у °^bs(9 . ) ) 2 =

= ^ ( Y ( P , 9 . ) - у ) ² ^ m i n. (2)

Asafigure-of-m ^j eritof LSM solution, according to [4], weighted difference of calculated and observed patterns (profile R-factor) is taken:

R =

£ ( у mod ( p , 9 j ) - у -- (о ) )

■100 %.

A necessary condition of extremum for (2):

m

\ dY(P, 9,) ;P, 9j))^Prj = 0, k = 1,..., N,

where P_k – k -th component of parameter vector P .

However, due to non-linearity of functions Y^. ( P , ) over parameters P derived system (4) cannot be solved analytically. Linearizing the system (4) by Taylor expansion at starting point P ₀ with truncating terms above first order, we can obtain a system of linear equations over N variables (non-linear least-squares method). Iteratively solving for P ₁ , P ₂ , …(refining values P : P ₁ = P ₀ + P ₁,…), we will move towards P* . Solution process convergence is defined by proximity of point P ₀ to optimal * . With starting point P ₀ declining and problem dimensionality N increasing the iterative method becomes unstable and starts to diverge. The bigger N (or the worse the quality of experimental data), the more precise P ₀ are required, which practical determination represents a serious obstacle.

Genetic algorithm of structure analysis. Effectiveness of evolutionary algorithms in complex non-linear global optimization problem solving was proven [2]. So the idea arose to combine the Least-squares method of seeking the minimum of functional (2) with evolutionary algorithm of objective function (3) optimization in order to solve abovestated problem. A two-level evolutionary algorithm comprising two distinctive genetic algorithms (GA) is suggested.

First level GA. The first level of proposed algorithm is a «conventional» hybrid GA [2; 3], dealing with binary representation of parameter values. Its chromosomes encode vector of sought parameters P , where binary representation accuracy is varied by user. In particular, fragments of chromosome define rounded with specified accuracy coordinates x , y , z of atoms of investigated material relatively to its elementary unit cell. Minimized objective function over P is R-factor (3), ideally tending to zero while converging toward a global minimum. R -factor is calculated unambiguously for each parameter vector P with given sampling Y ^obs ( ) and in practice, depending on simulation and experimental error magnitudes, should come to about 5...10 % (defined empirically) in optimal point.

A flow-chart of first-level algorithm is shown in figure 1 on the left. Starting population is generated arbitrarily, so a priori given starting approximations are not required. Tournament selection of parents with varied tournament size is employed. Algorithm, besides standard genetic operators – recombination (1– point, 2 – point or uniform) and mutation, uses local search operator. The best individual and some randomly chosen individuals are subjected to LSM local descent over all coordinates (modified Newton–Raphson algorithm). Lamarckian concept of evolution [2; 3] is implemented, where parameter values found by the local search replace old ones.

Primary objective for this level is to find plausible (in the sense of R-factor) initial approximations of parameters ₀ .

Second level GA. Evolutionary algorithm of the second level is utilized for the searching and generating of LSM refinement strategy for initial approximations of parameters ₀ , representing a sequence of local descents on R-factor hypersurface. Bit strings B _i defining groups of parameters refined on current generation are used as this level individuals. The length of a bit string equals to a number of sought parameters N with each bit corresponding to certain parameter. Bit value on a position k of the second individual indicates whether to refine (= 1) ornot(=0) the k -th parameter on a current iteration. The values of parameters P for the every string are refined iteratively with non-linear LSM from (4). For example, string 101 means that equations (4) are constructed only for k =1and k =3andaftersolvingof2*2systemgive increments for   1 and 3 parameters, while parameter of index

2 is left unmodified. Thus, each B _i defines a search sub-space.

A flow-chart of second-level algorithm is given in figure 1 on the right. Initially this level GA individuals can be generated arbitrarily or according to some empiric scheme based on user-provided patterns sequence (masks imposed on B _i ). For assessment of the GA individuals for each B _i a relation to first-level P _i individual (one or many) is set. For ( B _i , P _i ) pairs the LSM is applied according to above principles, with a result of P i' - refined P i values in accordance with B i string. Level 2 objective function takes into account an performance of applied LSM: as figure-of-merit (fitness) of the 2nd level individuals the function (5) is taken:

F = [ R ( P^ Z R ( P ) + p j"¹            (5)

where p – a penalty for non-convergence (substantial increase of local search steps lengths).

Thus, the better the refinement process convergence, the higher the assessed individual fitness. B – individuals are recombinated and mutated without P – individuals altering. Results of that evolution are the refinement strategies of P – individuals.

Objective for this level is to carry out a sequence of refinements (local searches over dimensions specified by bit string) using the best solutions from the preceding level. Providing sufficiently suitable initial approximations P ₀, the refined will converge to optimum. Unsuitable P ₀ with many refined parameters will not yield convergence; in this case, a subsequent executing of first level algorithm can give better initial approximations for second level. The best parameter strings are returned to the first GA level for assessment and inclusion in next population { _i }.

The proposed algorithm involves a cyclic executing of both levels while stop criteria are not satisfied (computational resource is exhausted, min R <  R _stop, mean R <  R ′ _stop). One or many better and some randomly chosen individuals are transferred to another level. Evolution of trial structures on the first level provides a search for values suitable for second level minimization by an evolutionary sequence of local searches. Moreover, this approach affords overcoming of local minima, where LSM can fall to during second level performing. Thus, stochastic and deterministic search procedures are combined here mutually complementing and enhancing each other.

The algorithm has been implemented as a shell over a DDM console program incorporating Rietveld-like method [5]. For the purpose of the algorithm performance evaluation it was tested on single- and multi-phase samples with known crystal structure of component phases (samples 1, 2).

Sample 1. A determination of crystal structure of component phases and quantitative phase analysis of three-phase sample CPD-1h, given by Commission on Powder Diffraction of International Union of Crystallography at Round Robin on QPA [6] quantitative phase analysis contest.

Simultaneously, profile parameters, coordinates of atoms in general crystallographic positions and thermal atomic parameters (29 parameters in total) were searched through all possible value ranges. A convergence plot for two-level GA indicating the R-factor decrease during parametric and bit strings populations evolution is given in figure 2. Itis clear that R-factor decrease is primarily provided with 2nd GA level, while 1st level efficiently leads out from local minima. An optimal solution was obtained after 5th full GA cycle. It was empirically drown that 3 generations on each GA level with population sizes of 20 1st level and 10 2nd level individuals are sufficient for reliable convergence of the method. Population sizes are comparable with the dimensionality of the problem that indicates an efficient usage of computational resource and substantial potential of the method. Time spent for the problem solving: 4 min 47 sec (CPUAMDX24400+).

On a final stage of the algorithm, the phase concentrations were calculated. A correspondence between true and found compositions serving as an integral quality criterion of obtained solution is shown in table 1. In the last table row the root mean square (RMS) is given.

It should be noted that RMS of phase analysis solutions from Round Robin on QPA for CPD-1 samples averages ~3%mass[6].

Sample 2. Crystal structure of single-phase sample Pd(NH₃)₂(NO₂)₂ [7] determination.

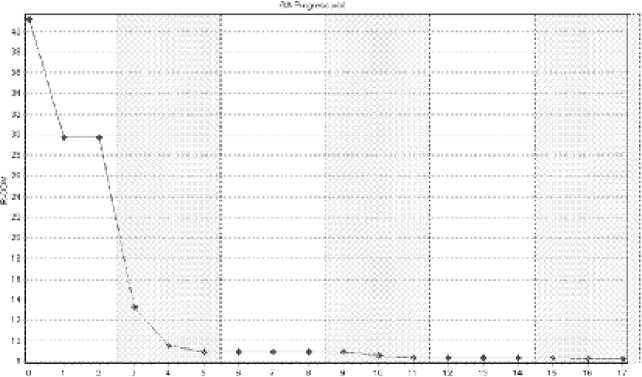
All coordinates of atoms in general crystallographic positions (including coordinates of hydrogen atoms) and thermal atomic parameters (26 parameters in total) were searched simultaneously. A corresponding GA convergence plot is demonstrated in figure 3. As in previous case, 3 generations of each level were generated on a full GA cycle. Used population sizes: 20 individuals on the 1st level and 10

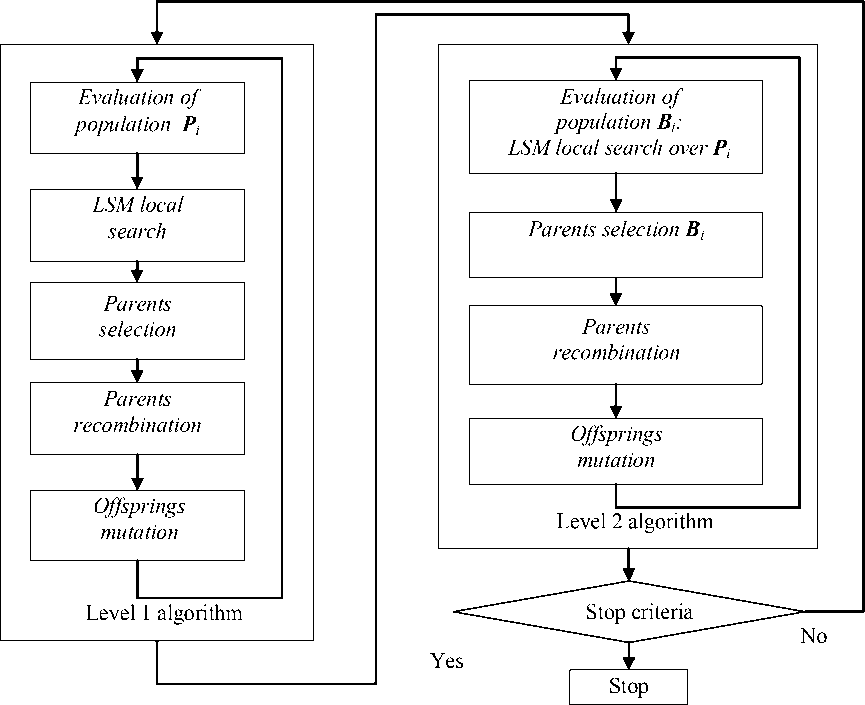
Fig. 1. Two-level GA flow-chart

on the 2nd level. An optimal solution was obtained after 3th full GA cycle. One can see that convergence here again is primarily provided by the 2nd GA level. Time spent: 4 min 21 sec(CPUAMDX24400+).

A correspondence between experimental and calculated X-ray powder patterns from the last GA stage is demonstrated in figure 4. It can be an integral quality criterion of obtained solution.

Found coordinates of the atoms (relative to the crystal cell axes) and thermal parameters compared to reference values [7] (designated with asterisks) are given in the table 2.

Obtained maximum error for coordinates of the heavier atoms: 0.0015, for thermal parameters: 0,012, and for coordinates of the hydrogen atoms: 0.0170.

The accuracy of obtained solution suits the accuracy of reference model structure [7]. It should be noted that with GA the coordinates of hydrogen atoms were found, which, being the lightest of all atoms, is hard to locate with available powder pattern analysis methods.

Described two-level GA comprises search and refinement of crystal structures thus giving the possibility of automation of structure determination process. Important features of

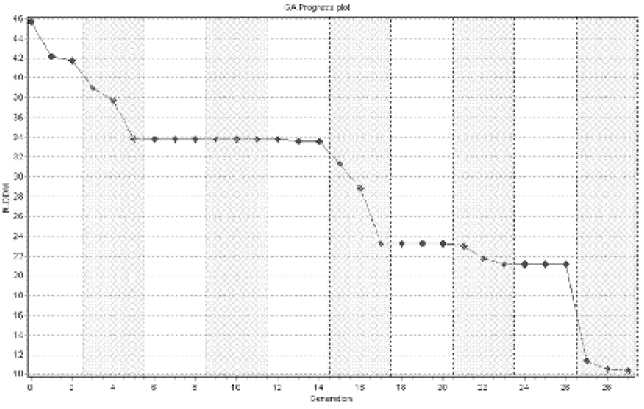
Fig. 2. GA convergence plot. The best found so far (to a current generation) solutions are designated (x-coordinate – the number of generation, y-coordinate – R-factor). Cross-hatching marks second-level GA executing

i"*»wttm

Fig. 3. GA convergence plot. The best found so far solutions are designated. Cross-hatching marks second-level GA executing

Table 1

CPD-1h sample composition

Phase Formula True (% mass) Found (% mass) Error (% mass) Corundum Al2O3 35.12 35.39 0.27 Fluorite CaF2 34.69 35.08 0.39 Zincite ZnO 30.19 29.53 0.66 RMS 0.57 algorithm are, as well, the possibility of simultaneous search of profile and structure parameters, and in case of multiphase samples, phase composition calculation. It seems that the key role here was played by the combination of first and second level algorithms. Apparently, proposed approach has substantial potential for further development.