Учет ближнего порядка в расположении атомов в термодинамике бинарных растворов замещения

В термодинамике твердых растворов замещения широко используется понятие регулярных твердых растворов [1]. Под этим термином понимают бинарные растворы, для которых молярную свободную энергию можно записать в следующем виде:

G_m = ^AG_O(1-9_B)+ ^BG₀9_B + RT(% 1п9_в +

+ (1-9_в)1п(1-9_в)) + Л9_в(1-9_в), (1) где ^AG₀ и ^bG₀ - свободные энергии чистых металлов А и В с той же решеткой, что имеет твердый раствор; 0_В - атомная доля компонента В; R - универсальная газовая постоянная; Т - абсолютная температура.

Сумма двух первых слагаемых отражает свободную энергию механической смеси металлов А и В. Третье слагаемое, всегда отрицательное, отражает энтропийное слагаемое (-Т8_ИД) для идеальных твердых растворов. Четвертое слагаемое, которое дая регулярных растворов имеет специфический вид, отражает теплоту (или энергию) смешения. В квазихимической модели парного взаимодействия под параметром Л понимают величину

Л = |а_ое, (2) где z - координационное число решётки; А_о - число Авогадро; 8 - это энергия взаимообмена атомов, или энергия смешения,

• ⁸ ~ (28_АВ - 8_АА - 8_ВВ ). @) Она представляет изменение энергии, которое возникает, если разорвать связь между парами атомов А А и ВВ и создать две пары атомов АВ.

Величина 8 и соответственно Л могут быть либо положительными, либо отрицательными. Случай Л<0 соответствует упорядоченным, а случай Л > 0 - расслаивающимся растворам. Если бы четвертое слагаемое не зависело от температуры, то его можно было бы однозначно определить как теплоту смешения, но в физической химии этот параметр часто оказывается температурно зависящим. В химической термодинамике [2] существует соотношение

ДН = -Т2—(—\ (4) ат\ ту из которого в случае линейной зависимости параметра Л от температуры вида Л = Ао +РТ следует, что теплота смешения

ЛЯ = -Т¹ —( = Л₀9_в(1 - 9_В)

СМ гт-1 I и 15 х £5 / О1\ I )

не зависит от температуры. Таким образом, параметр Л(Г) содержит и энергетическую (Л_о), и энтропийную (-РТ) составляющие, поэтому его часто обозначают как AG,, то есть как избыточную свободную энергию по отношению к идеальному твердому раствору. Для краткости назовем эту величину кажущейся теплотой смешения. Далее будем рассматривать твердые растворы произвольного элемента i в железе, для которых доля атомов i равна 0„ а железа - 0_Fe.

Уже давно известно [2], что модель регулярных растворов является внутренне противоречивой: если Л меньше нуля, то должна существовать тенденция преимущественного окружения атомов А атомами В, и наоборот. Это, безусловно, должно привести к уменьшению энтропии по отношению к идеальному раствору и к увеличению по модулю отрицательной энергии смешения. Отсюда следует, что в термодинамике растворов необходимо учитывать ближний порядок во взаимном расположении атомов. Первые работы в этом направлении (квазихимическая теория) выполнены Лившицем [3] и позже Жуховицким [4]. Отметим также работы, сделанные Гельдом [5] и Кожеуровым [6]. М.А.Штремель с сотрудниками [7] для описания ближнего порядка использовали параметр р^-Ь представляющий вероятность события, что в твердом растворе замещения в данном соседнем с атомом Fe узле расположен атом растворенного элемента I. Для равновесного состояния Штремель получил следующее выражение

• -1 + 71 + 4е*(1-0,)А _ 2(1-0,)/? ’ ^{( }}

где h = exp — -1; к - постоянная Больцмана. ХкТ)

Для избыточной свободной энергии раствора оказалось справедливым выражение

AG = -0/7?7’-1п^^^- +

2 '        0, -0Fe6,

4+(1-0,)ЯГ.1пЬ^.            (6)

2                1 — U.

Аналогичное соотношение было получено В .А. Кожеуровым. В случае, если рассматриваются очень высокие температуры (а тогда величина h мала) или малые концентрации второго компонента (а тогда мал параметр 46z(l-6z)/z), можно использо вать разложение радикала в ряд по малому параметру. В итоге получается выражение, которое используется в теории регулярных растворов:

дс,-^|8е,9Ре=леЛе-           (7)

Следовательно, при учете ближнего порядка формулы для регулярного раствора возникают при малом значении параметра 40z (1 - 0Z )Л.

В связи с этим возникает вопрос: как описать простой формулой изменение AG, при промежуточных температурах? При этом важно иметь в виду, что в области низких температур (ниже 700 К) установление ближнего порядка кинетически невозможно [7] и сплав сохраняет то же значение ближнего порядка, которое он имел при температуре замораживания. Подобные расчеты, безусловно, проводились и раньше, но в очень ограниченных температурных и концентрационных областях. Наличие современной компьютерной техники позволяет выполнить эти расчеты более детально, в частности, установить, какова реальная температурная зависимость AG, (теплоты смешения) и не обусловлена ли наблюдающаяся температурная зависимость этой величины исключительно изменением ближнего порядка.

Эти расчеты были проведены для ОЦК твердых растворов Fe-Cr. По данным [8], для них Л = 25100-11,72-7 Дж/моль, откуда E = N_oe = = 6275-2,93-7 Дж/моль. При расчетах мы сознательно не учитывали температурную зависимость е, то есть приняли Е = 6275 Дж/моль и, используя формулу (6), рассчитали:

• 1)    концентрационную зависимость избыточной свободной энергии (теплоты смешения) при различных температурах (рис. 1);

• 2)    температурную зависимость теплоты смешения для сплавов нескольких составов (рис. 2).

Зависимость AG, от концентрации имеет качественно такой же вид, как и для функции А0Сг(1-0Сг) в модели регулярных растворов (см. рис. 1). Если перестроить эти графики в коор-

AG, динатных осях ---------- и 0Сг, то вместо гори-

6Сг бег)

зонтали (+25 100) наблюдается целая группа слегка наклонных линий, которые при температурах от 5000 до 700 К расположены недалеко от этой горизонтали. Поскольку термохимические измерения всегда имеют погрешность, то экспериментаторы вполне могут допустить, что отношение AG

--------- является примерно постоянным при ^СгО~®Сг)

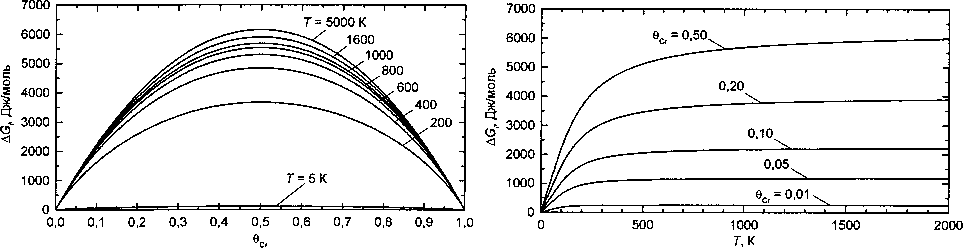
Рис. 1. Зависимость кажущейся теплоты смешения Рис. 2. Зависимость энергии смешения от температуры от концентрации хрома при различных температурах при различных концентрациях 0Сг (указаны у кривых) (указаны у кривых)

всех температурах, и таким образом сделать вывод о том, что имеют дело с регулярным раствором. Очень сильные отклонения наблюдаются ниже 700 К, но при таких температурах перераспределение элементов идет чрезвычайно медленно, то есть такие измерения невозможны, и твердый раствор оказывается замороженным. Итак, мы видим, что при постоянной энергии взаимообмена 8 учет ближнего порядка приводит, тем не менее, к почти регулярному раствору. Для кривых температурных зависимостей AG, (см. рис. 2) отметим удивительный результат: при стремлении к 0 К в условиях равновесия теплота смешения стремится к нулю. Это означает, что при 0 К сплав разделился на участки практически чистого Fe и чистого Сг, которые, конечно, контактируют друг с другом, но с понижением температуры число точек контакта уменьшается. С повышением температуры AG, начинает возрастать, эта зависимость, довольно крутая при низких температурах, выше 500...700 К переходит в плавную, причем при очень высоких температурах величина Л стремится к верхнему значению 25 100 Дж/моль. Таким образом, учет ближнего порядка должен привести к сильному отклонению поведения раствора от регулярного, но в той температурной области, где из-за малой скорости диффузии фактического изменения ближнего порядка происходить не может.

Особенно наглядно температурная зависимость проявляется, если рис. 2 представить в иных

AG, координатных осях: ------ ---Т (рис. 3). Здесь

6Сг(1-6Сг)

^Gi видно, что параметр ---------- выше 700 К сла бо-О” @Сг)

бо увеличивается с повышением температуры. Но вблизи 0 К он резко снижается и обращается в 0 при 0 К. И в этом случае, если работать выше 700 К, то растворы можно считать регулярными, но для параметра А придется задать слабую температурную и концентрационную зависимость.

Рассмотрим более подробно природу температурной зависимости параметра А (теплоты смешения). Подставим выражение (5) в (6) и преобразуем последнее к виду

AG, = — RT$ In------— +

' 2 v2А9

2(1 - 9, )А +1 - J1 + 49,(1-9,)A +(1-9,) In —---2-----л.„ д(8)

'           2(i-9j2a

Считая, что величина у = 40, (1 - 0, )Л «1, используем разложение в ряд [9] функции ^fi + y :

с----- 1 1       1 2 1 з

1 +у = 1 + — у—у + — у -

2    8     16

5 ₄ 7 ₅ -У +—У 128    256

и представим выражение (8) в форме

AG, =|/^{е,ь[1 + (1-0У/г-29Х1-9,)3й2 +

+59,2 (1 - 9, )4 А3 -149/ (1 - 9, )5 А4 ] + (1 - 9,) х х In [1 + 9, 2 А - 29,3 (1 - 9, )А2 + 59,4 (1 - 9, )2 А3 -

-149,5(1-9,)5А4]}.(10)

Далее, чтобы избавиться от логарифмической функции, приходится использовать еще одно разложение в ряд [9]:

2     34

1п(1 + у) = у-^-+^--^- + .„,(11)

причем в разложениях (9) и (11) следует удержать сумму такого количества слагаемых, которая обеспечит требуемую точность расчетов. Если, например, ограничиться первым членом разложения в формуле (11), а в (10) оборвать ряды под логарифмом на втором слагаемом, то получим соотношение

AG, = | RT ( 9, (1 - 9, )² А + (1 - 9, )9_;² А) =

= 9,(1 -9, )2rj I expf — |-1 I, 2 I (7?rJ J

известное в теории ближнего порядка [6, 10, 11].

На рис. 4 результаты расчета по точной формуле (6) и формуле первого порядка приближения (12) для сплавов Fe-Cr сравниваются между собой. Заметно значительное расхождение результатов, и только при Т -+ оо результаты совпадают.

Главная причина, по которой вывод формулы (12) не точен, состоит в том, что при 8^0 всегда существует интервал температур, в котором величина \h\ оказывается порядка 1. В этом случае слагаемое у — (1 —0,)2/z, входящее в первую логарифмическую функцию в выражении (10), нельзя считать малым, поэтому использование формулы (11) дает заметную погрешность. Для второй логарифмической функции в выражении (10) такой проблемы нет, так как слагаемое ^h действи тельно мало.

Если раскрыть степени (1-0,)" по формулам бинома Ньютона в выражении (10) для первой логарифмической функции, то выясняется возможность представить ее в виде произведения ln((l + /z)F), где

F = 1-20,А + 0,²й + 50,²Л² -60,³Л² ~ 140/Л³ +

+ 2Q*h² + 280,⁴ И³ + ...,                    (13)

а затем, использовав (11), можно разложить функцию F в ряд по параметру у, который теперь действительно становится малым. Ограничившись членами с 0³, найдем

InF =-2А0,+(Л+ЗЛ2)0,2 -

4А2+уА3)9,3+...                (14)

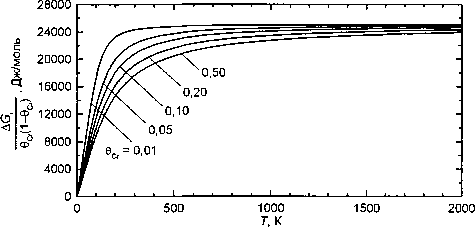
Рис. 3. Зависимость параметра -..............-...................^................- от температуры при различных концентрациях во (указаны у кривых)

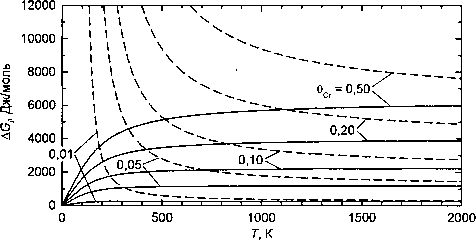
Рис. 4. Зависимость энергии смешения от температуры при различных концентрациях вСг (указаны у кривых). Сплошные и пунктирные линии - расчет по формулам (6) и (12) соответственно

Для второй логарифмической функции проведем аналогичное разложение

In F₂ «9²h-29,³h² + 0,⁴(2А² + 5й³),      (15)

и тогда для АЦ получаем следующее, значитель но более точное, чем (12), выражение:

^Gi

-RT 2

0, —+ 0X1-6, Х-А9/ +

+(h2 -h)e,2 ™h39b

Результаты расчетов по этой приближенной формуле и по точной (6) сравниваются для малых 6 на рис. 5.

Теперь степень согласия результатов резко улучшилась. При концентрации 0Сг <0,1 для температур выше 500 К кривые, рассчитанные по точной (6) и приближенной формуле (16), практически совпадают. Теплота смешения выше 500 К все же имеет температурную зависимость, хотя и слабую, но противоположную той, которая наблюдается у определенного термохимическими методами параметра Л. Можно сделать вывод, что энергия взаимообмена е все же имеет температурную зависимость, обусловленную, вероятно, магнитными эффектами или особенностями колебаний атомов.

Аналогичные расчеты были проведены и для от рицательной энергии смешения Nos = -6275 Дж/моль. Нужно отметить, что при концентрациях 0Z <0,3 приближенная формула (16) дает результаты, почти совпадающие с расчетами по точной формуле (6), причем формула (16) для отрицательных Е гораздо точнее воспроизводит температурную зависимость NGt, чем в случае положительных значений энергии.

Наличие температурной зависимости у рассчитанной с учетом ближнего порядка энергии смешения приводит к необходимости рассмотрения следующей задачи. Допустим, что на основе термодинамических измерений показано, что твердый раствор является регулярным и экспериментально установлена величина энергии смешения. Существование теплоты смешения свидетельствует о взаимодействии (притяжении или отталкивании) между атомами растворителя и растворенного элемента. Следовательно, в твердом растворе должен существовать ближний порядок, параметр которого определен, например, уравнением (5), в которое входит энергия взаимообмена 8 (на атом) или Е (на моль). Для того, чтобы обеспечить независимость теплоты смешения от температуры, энергия взаимообмена Е, напротив, должна быть слабо температурно зависящей (как показано на рис. 3). Поэтому возникает проблема определения зависимости энергии взаимообмена Е от темпера-

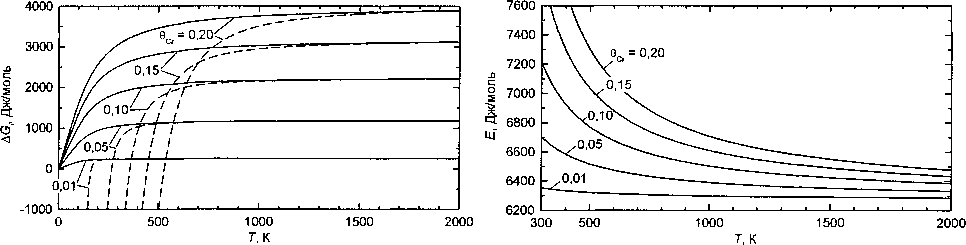
Рис. 5. Зависимость энергии смешения от температуры при различных концентрациях вСг (указаны у кривых). Сплошные и пунктирные линии - расчет по формулам (6) и (16) соответственно

Рис. 6. Зависимость молярной энергии взаимообмена Е от температуры при различных концентрациях в_Сг (указаны у кривых)

туры, такой, чтобы теплота смешения была бы постоянной или имела определенную в экспериментах зависимость.

Чтобы решить эту обратную задачу, используем разложение в ряд функции к.

, Е \ EY 1 Е\ h =--1— --- 4— --- + ...        (17)

RT 2\RT ) 6VRT)

После подстановки этого разложения в выражение (16) и расчета необходимых степеней сумм удается сгруппировать слагаемые так, чтобы они располагались в порядке возрастания малости:

z           z Е2 п п

AG, =-£6(1-6)--—62(1-6)2-

--^-^е2(1-е)2(1-бб(1-б)),      (18)

12 ^RTf причем, как показывают оценки, в этом ряду достаточно ограничиться двумя членами. Приравняв эту сумму величине Л9(1 - 0) и сократив левую и правую части на 0(1 - 0), мы получим квадратное уравнение относительно Е. Интересующий нас корень уравнения равен

RT ( L 4Л6(1-бГ 6(1-6)^ V zRT ,

На рис. 6 приведены результаты расчетов, показывающие, какой должна быть температурная зависимость энергии взаимообмена для того, чтобы теплота смешения компонентов не зависела от температуры.

Работа выполнена в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы и поддержана грантом РФФИ 10-03-00295-а.