Учет числа пролетов воздушной линии электропередачи при определении наведенного напряжения

Воздушная линия электропередачи (ЛЭП) является источником кондуктивных и индуктивных помех. Расчет индуктивных помех необходим для обеспечения надежного функционирования устройств релейной защиты и автоматики, передачи информации по каналам связи, обеспечения безопасности при проведении работ на оборудовании и электрических сетях, находящихся в зоне влияния воздушной линии электропередачи.

На отключенную воздушную ЛЭП от функционирующих в непосредственной близости от нее соседних линий наводится напряжение, которое складывается с напряжением самой линии. Такое напряжение называется наведенным.

В связи с этим правила по охране труда при эксплуатации электроустановок (ПОТЭУ) предписывают комплекс защитных мероприятий, которые необходимы для обеспечения безопасности при проведении работ на воздушных ЛЭП. Отдельно отмечаются меры безопасности в случаях, когда заземление проводников не позволяет снизить значение наведенного потенциала на отключенной линии ниже 25 В.

Практика эксплуатации воздушных ЛЭП показывает, что каждый год обслуживающий персонал получает электротравмы вследствие наведенного напряжения, приводящего к протеканию через тело человека электрического тока. Появление наведенного напряжения связано с электростатическим и индукционным воздействием от воздушной линии, которая проходит в непосредственной близости, на отключенную ЛЭП.

Электромагнитное поле влияющей линии связано с ее напряжением, током, топологическими особенностями. Кроме этого, большое значение играет длина участка сближения влияющей и отключенной линий. На каждом проводнике отключенной линии наводится потенциал, который определяется суммой двух составляющих: электростатического и электромагнитного взаимодействий [1].

Электростатическая составляющая наведенного напряжения связана с взаимодействием электрической составляющей электромагнитного поля влияющей линии на рассматриваемый проводник отключенной. Значение этой составляющей, даже при соблюдении требований правил устройства электроустановок (ПУЭ), при параллельном прохождении линий зависит, в первую очередь, от напряжения на влияющей линии и коэффициента емкостной связи. Точное определение коэффициента емкостной связи возможно только в случае определения электрического поля влияющей линии с учетом всех ее топологических особенностей, в частности стелы провеса проводников. Электростатическая составляющая наведенного напряжения может быть снижена до безопасного значения на всей линии путем ее заземления в любом месте. При заземлении отключенной линии по обоим концам действие электростатической составляющей будет полностью нивелировано.

Электромагнитная составляющая наведенного напряжения связана с взаимодействием магнитной составляющей электромагнитного поля влияющей линии на рассматриваемый проводник отключенной. В этом случае решающее значение имеет коэффициент индуктивной связи и ток, протекающий по проводникам влияющей линии.

Анализ модели расчета наведенного напряжения

На основе методов, изложенных в [2], возможно уточнить типовую методику расчета наведенного напряжения.

Исходными данными для расчетов являются расстояния между осями трасс ВЛ на участках сближения, длина ВЛ, значения сопротивлений контуров заземления опор и подстанций, находящихся по концам линий и на границах участков, а также значения токов, которые могут протекать во влияющих ЛЭП. Для сетей произвольной топологии расчет значений наведенного напряжения на отключенной ЛЭП производится на основе упрощенной схемы замещения, полученной на основе П-образной схемы замещения. В этом случае воздушная линия электропередачи разделена на два участка с различными удельными наведенными ЭДС.

С практической точки зрения целесообразно учитывать только магнитное влияние, поскольку, как показано в [1], электростатическое влияние более чем в 50 раз менее интенсивно, чем магнитное при выполнении требований ПОТЭУ по установке заземления на отключенной ВЛ. Магнитное влияние в большей степени определяется продольной составляющей вектора напряженности электрического поля от влияющих линий Eх, которая без учета токов смещения определяется дифференциальным уравнением d2E

x dy2

+

d ² E x

dz ²

k 3 E x = 0,

где k 3 = д/ j o^c 3 - волновое число земли; а 3 - удельная проводимость грунта земли; го - циклическая частота; μ ₀ – магнитная постоянная.

Решение уравнения при принятии допущения о горизонтальном расположении проводников влияющей и отключенной ВЛ можно представить в виде

I k = j

» e -v ( h + z )

cos yvdv .

0 v + V v² + k X

Зная E_x , однозначно определяем эквивалентную ЭДС, наводимую в проводнике отключенной ВЛ при прохождении ее параллельно влияющей ВЛ:

Ei = Exl , где l – длина участка влияющего проводника, так же и в случае сходящихся влияющей ВЛ и отключенной ВЛ:

yb

Ei = ctga j Exdy,

ya где α – угол между влияющей и отключенной ВЛ; ya, yb – минимальное и максимальное расстояния между влияющей и отключенной ВЛ на сходящемся участке.

В [3] показано, что с погрешностью, не превышающей 5 %, интеграл Карсона (3) может быть представлен в виде

. ( h + z + _r) 2 + yy

I k = j ^b ----k ----2

.

⁴     ( h + z ) + y

После подстановки (2, 6) в (4) получим соотношение для определения ЭДС, создаваемое магнитным полем (МП):

Ei=- j ^

4 n

, ( h + Z ) 2 + У 2 . ^{( h + Z +} l 3 ^{)2 +} У ' n( h - z )² + y ^{2 +} n ( h + z )² + y²

I i l i =- ад , .

Более точное определение ЭДС, создаваемой магнитным влиянием, возможно произвести, зная распределение векторного магнитного потенциала А от влияющей линии. Зная векторный магнитный потенциал, можно определить магнитный поток, пронизывающий некоторую площадь. Далее можно рассчитать собственную и взаимную индуктивность.

Для более точного расчета магнитного поля необходимо учитывать, что провод, жестко закрепленный в двух точках на разной высоте и испытывающий равномерно распределенную нагрузку как собственного веса, веса гололеда, так и давления ветра имеет стрелу провеса. Жесткость поперечного сечения проводов, используемых для транспорта электроэнергии, меньше равномерно распределенной нагрузки. Механическое напряжение в произвольной точке обусловлено только растяжением и направлено по касательной к кривой в рассматриваемой точке.

При расчете параметров магнитного поля, создаваемого влияющей линией электропередачи, в качестве математической модели реального проводника будем использовать уравнение идеально гибкой нити

Определим параметры МП с учетом провисания проводников линии электропередачи. Для этого получим выражение вектора магнитной индукции магнитного поля, создаваемого единственным проводом одного пролета. Величина тока, протекающего по проводнику, известна. Вектор магнитной индукции связан с векторным магнитным потенциалом

B = rot/ 1 .

Определим выражение для векторного магнитного потенциала. Для определения этого потенциала разобьем проводник на малые токовые участки Idl , касательные к проводу в точке (x,y,z) (рис. 1). Этот токовый отрезок создает элементарный векторный потенциал dA :

dA лл м

4п г где µ0 =4π·10-7 Гн/м – магнитная постоянная; µ – относительная магнитная проницаемость воздуха, в дальнейших расчетах примем ее равной единице.

Поскольку проводник находится над поверхностью идеальной земли, то ее влияние заменим зеркальным изображением I dl , который создает в расчетной точке векторный потенциал dA ' . Ток I' меньше по модулю тока 1 на величину

^Ц зем    ^Ц возд

Ц зем + Цвозд где µвозд – относительная магнитная проницаемость воздуха, для практических расчетов она мало отличается от единицы; µзем – относительная магнитная проницаемость грунта земли.

При распространении электромагнитных волн промышленной частоты токи проводимости преобладают над токами смещения, поэтому происходит лишь незначительное ее проникновение в глубь земли. Следовательно, грунт для электромагнитных волн низкой частоты мож- цц Idl'

но рассматривать как проводник. Таким образом, к ^ 1, значит, I = 1 и dA - =    --- .

4 п r

Результирующий векторный потенциал в точке M от элементарного участка с током и его изображения определим по принципу суперпозиции dA = dA + + dA - = idA X + jdA Y + kdA Z .

Проекции векторного магнитного потенциала

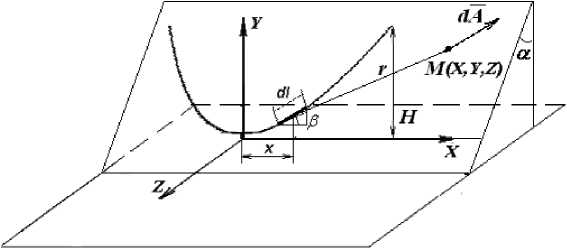
Рис. 1. К определению магнитной индукции от одного пролета

Fig. 1. To the magnetic field determination from the one span

– 350 –

ОО       11 1 ОО         I 11

dA X ----- Idl cos в — + — I ; dA Y ----- Idl sin p cos a l---

4 п I r r ')          4 п                I r r ‘

I 1 1 1

dA7 -----Idl sin в sin al - + — I, Z   4п              Ir  r'/ где r - расстояние от токового элемента до точки M(X, Y, Z)

r -д/ ( X - х ^{) 2} + ⁽ Y - у ^{) 2} + ( Z - z ^{) 2 ;}

г' - расстояние от изображения токового элемента до точки M(X, Y Z) r '-V( X - x ) 2 + ( Y + y ) 2 + ( Z -) 2 .

Проекции векторного магнитного потенциала определим интегрированием по всей длине проводника:

L

A_X - ^{00 0} i f                              ¹

на ox ' -M ^X - ^x ) 2   Y ^-( kx 2 ⁺ h ^{) co}s ^a M Z ^- ( H под - kx 2 ^- h )- ^a H

V((X - x)2 + (Y + (kx2 + hr )cos a)2 + (Z - (Hпод - kx2 - hr )sin a)2 ), dx

на 0Y

на 0Z

A A = ЯП Ik cos _a . 2

—

AZ

+

x

L

/

ЯП      f

=--- Ik sin a

2 n            ^J,.

—

x

—

I cos a ) 2 ⁺⁽ Z ^— ( H,

I cos a ) +⁽ Z ^{— (} H под

—

kx ²

—

—

A

h^Of])

x

x

kx ²

dx

⁺ ha ^{) cos a ) 2 +(} Z ^{— (} H под

I^cos a ^{) 2 +(} Z ^{— (} H под

—

kx ²

—

—

, (16)

+

—

kx ²

—

.

h )m a ) ' ) J

dx =

В декартовой системе координат ротор имеет вид rotA = i j k

А £ d x d у д z A x A y A z

Следовательно, проекции вектора магнитной индукции

ВА   8А   п   0Лх  дAz 0Ay  0А

В_х =          ^у- ; Б_у =          z -; B_z = -А- .

X д Y  дZ ^Y   дZ  дX    Z дX  д Y

Модуль магнитной индукции в произвольной точке

Б ( M ) = V B X + B Y + B Z .

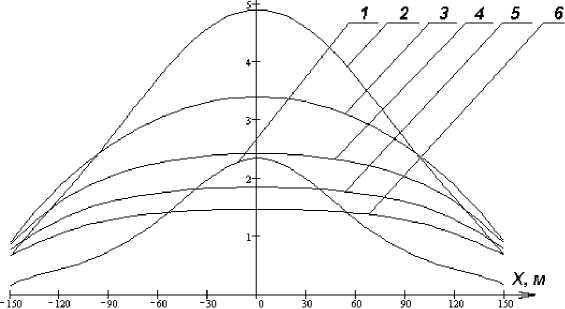
На рис. 2 изображены зависимости вектора индукции магнитного поля В ( X , const , const ) от расстояния вдоль единичного пролета Х , на постоянной высоте Y =1,8 м, для различных расстояний до плоскости провеса провода Z , при допущении, что стрела провеса проводника вертикальна (ее координата z = 0).

Рисунок 3 демонстрирует зависимости вектора индукции магнитного поля В ( const , const , Z ) от расстояния до плоскости провода Z при высоте расчетной точки 1,8 м

Ав. мкТл

• 1)    Z = 0 м; 2) Z = 10 м; 3) Z = 20 м; 4) Z = 30 м; 5) Z = 40 м; 6) Z = 50 м

Рис. 2. Зависимость вектора магнитной индукции вдоль единичного пролета от расстояния до плоскости провода на высоте 1,8 м

Fig. 2. The dependence of the magnetic induction vector along the single span on the distance to the wire plane at a height of 1.8 m

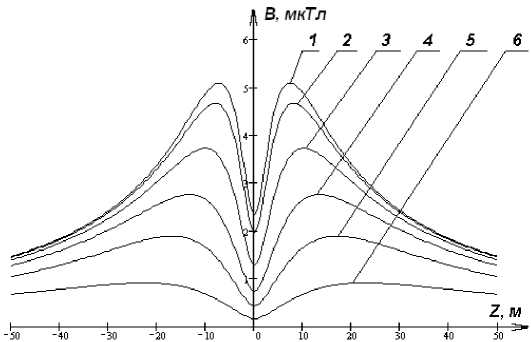
• 1)    X = 0 м; 2) X = 30 м; 3) X = 60 м; 4) X = 90 м; 5) X = 120 м; 6) X = 150 м

Рис. 3. Зависимость вектора магнитной индукции от расстояния до плоскости провода, от расстояния вдоль единичного пролета на высоте 1,8 м ^,

Fig. 3. The dependence of the of magnetic induction vector on the distance to the plane of the wire and on the distance along a single span at a height of 1.8 m для различных расстояний вдоль единичного пролета X при допущении, что стрела провеса вертикальна.

Число пролетов необходимо учитывать при расчете вектора магнитной индукции магнитного поля.

На рис. 4 показано несколько кривых распределения индукции магнитного поля в случае учета магнитного поля нескольких смежных пролетов.

Из данных графика следует, что учет более трех пролетов (двух смежных) практически не влияет на точность расчетов. В качестве эталонных значений величины индукции магнитного поля ВЭТ приняты такие, которые были получены при учете десяти смежных пролетов. Относи- тельную погрешность ε при этом рассчитаем как ε=

Bэт

-

B

B

100 %, где B – вектор магнитной

эт

индукции, вычисленный для числа пролетов меньше 21.

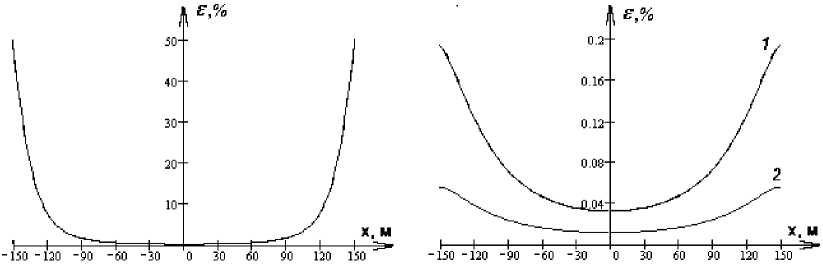
На рис. 5 изображена относительная погрешность индукции магнитного поля от расстояния до оси симметрии.

Зависимость В(Х) является периодической четной функцией с периодом, равным длине габаритного пролета [4]. После разложения в ряд Фурье и применяя численные методы вычисления интегралов, возможно определить коэффициенты a :

п п Х a_n cos _l .

”

В ( Х ) = a ⁰ + Z

²     n = 1

Поскольку параметры МП изменяются в зависимости от координаты Х и известно среднее значение на всем протяжении под пролетом, равное постоянному члену В_ср= а₀/2 , определим среднюю высоту подвеса проводника Н ср для горизонтально расположенного проводника, который создает в расчетной точке такое же МП.

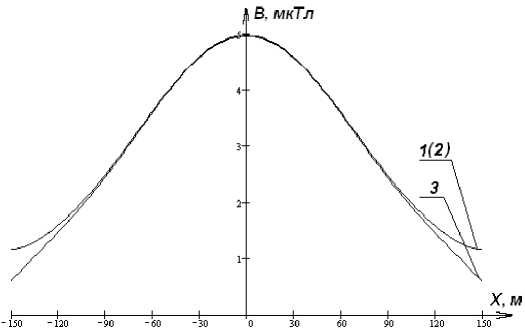
Рис. 4. Продольная эпюра распределения вектора магнитной индукции МП ВЛ при учете: 1) пяти пролетов; 2) трех пролетов; 3) одного пролета

Fig. 4. The longitudinal diagram of the overhead power line magnetic induction vector distribution 1) five spans; 2) three spans; 3) one span

a)

б)

Рис. 5. Относительная погрешность вектора магнитной индукции при учете: а) одного пролета; б) 1 – трех пролетов, 2 – пяти пролетов

Fig. 5. The magnetic induction vector relative error considering: a) one span; б) 1 – three spans; 2 – five span

Индукция магнитного поля от горизонтального проводника с учетом влияния земли на a— I  Z поверхности земли и расстоянии Z от его оси Вер = 2--2    2-.

^{2 п} Z + H ср

Среднюю высоту подвеса провода определим, приравняв последнее выражение к постоян-

" Z - _г 2 .

П В ср

ной составляющей а 0 /2. Получим H_ср

Заключение

Из анализа графиков, приведенных на рисунках, можно сделать следующие выводы:

• – индукция магнитного поля максимальна не в плоскости нахождения провода, а на незначительном расстоянии от нее;

• –    на расстоянии, приблизительно равном трети длины габаритного пролета от провода, индукция МП уменьшается не более чем в два раза от максимального значения;

• –    минимальных значений магнитная индукция достигает вблизи поверхности земли;

• –    при учете одного пролета минимальная погрешность составила 0,29 % непосредственно под стрелой провеса; максимальная погрешность достигает 50 % и наблюдается вблизи точек подвеса провода; с точностью ≈5 % влияние только одного пролета можно учитывать на 75 % длины пролета;

• –    при учете влияния более двух смежных пролетов погрешность становится пренебрежимо малой, ε ≈ 0,2 %, и, следовательно, при расчетах, связанных с определением наведенного напряжения, достаточно учитывать только три пролета.