Учет действительных свойств нагружающих систем при численном решении краевых задач методом конечных элементов

Следуя авторам [1], назовем совокупность твердых, жидких и (или) газообразных тел, деформирующихся в результате передачи нагрузки рассматриваемой телу или области, нагружающей системой. Для анализа устойчивости процесса деформирования, оценки результатов воздействия на механическую систему различных возмущений необходима информация о законе изменения внешних усилий при изменении свойств нагружаемого тела. Характеристики нагружающей системы при решении краевых задач механики неупругого деформирования и разрушения неоднородных сред можно учесть введением в граничные условия характеризующего «оператора влияния», устанавливающего связь силовых и кинематических величин во всех точках нагружающей системы, которые непосредственно вступают в контакт с исследуемой областью.

Локальные и нелокальные определяющие соотношения второго рода. Рассмотрим область Q , заполненную композиционным материалом. Если в качестве нагружающей системы выступает упругое тело Q , контактирующее с исследуемой областью Q по границе 5Q , то действительные усилия S ( r ) и перемещения u ( r ) , возникающие в каждой точке r е dQ , определяются соотношениями [1, 2]:

Si (r) = Si (r)- J ^/'(r,r') uj (r')d(dQ) , ui (r) = ui (r)- J Gzj (r,r')Sj (r') d(dQ) . (1)

SQSQ

Здесь S ⁰ ( r ) и u ⁰ ( r ) - номинально задаваемые (вне зависимости от деформации или сопротивления) на границе dQ усилия и перемещения соответственно, связанные следующим образом:

S,”(r) = J N«(r.Г')«0(r')d(an),    u0(r) = J G,j(r,r')S”(r')d(dQ).(2)

5Q5Q

В случае, когда при решении краевых задач нет необходимости учитывать характеристики нагружающей системы (предельно «мягкое» или предельно «жесткое» нагружение), в уравнениях (1) будут отсутствовать вторые слагаемые. При этом граничные условия по форме будут совпадать с классическими локальными граничными условиями в напряжениях и перемещениях.

Построение дискретных образов граничных тензор-функций Грина G(r,r') и Неймана N( r, r') области fQ, входящих в граничные условия (1) и полностью характеризующих нагружающую систему, представляет самостоятельную задачу, которая в случае дискретного представления эквивалентна задаче нахождения матрицы влияния (жесткости [3]) А.А. Ильюшина [4] или матрицы жесткости подструктуры (суперэлемента) [5–7].

Граничные условия (1) устанавливают связь между силовыми величинами во всех точках поверхности dQ , поэтому эти уравнения являются определяющими соотношениями второго рода, специально вводимыми для точек деформируемого тела, принадлежащих поверхности.

В работах [1, 2] представлена локальная форма уравнений (1) – граничные условия контактного типа

^[ ° и ⁽ r ) n j ⁽ r ) + R ij ^{( r} ) u j ^{( r} Я ^ = S i ^{( r} ) , ^[ u i ^{( r ) +} Q ij ^{( r} ) ° jk ^{( r} ) n k ^{( r ) ]}|_5n = u i ^{( r} ) , ⁽³⁾ которые также могут быть классифицированы как локальные определяющие соотношения второго рода . Эти граничные условия дополняют постановку краевой задачи информацией о характеристиках жесткости R ( r ) или податливости Q ( r ) нагружающей системы , которые удовлетворяют следующим условиям :

^{V a} * 0 : R ij ^{( r} ^aiaj > 0, Q ij ^{( r ) a}i a j >  0 (4) и связывают между собой номинально задаваемые в каждой точке r поверхности dQ тела усилия S ⁰ ( г ) и вызванные этими усилиями перемещения u ⁰ ( r )

S i ^{0 ( r ) =} R ij ^{( r} ) ^u 0 ^{( r} ) , u i ^{( r ) =} Q ij ^{( r} ) ^{S 0 ( r} ) , R ik ^{( r} ) Q kj ^{( r} M ij . ⁽⁵⁾

При R ( r ) = 0 или Q ( r ) = 0 граничные условия (3) соответствуют предельно «мягкому» или предельно «жесткому» режимам нагружения, а по форме совпадают с классическими локальным граничными условиями механики деформируемого твердого тела в напряжениях и перемещениях. Кроме того, из соотношений (5) следует, что уравнения (3) являются взаимно обратными, поэтому можно использовать граничные условия только одного вида для всей поверхности 5Q деформируемого тела.

Учет нелокальных граничных условий при численном решении краевых задач методом конечных элементов. Для разработки способа учета нелокальных граничных условий (1) воспользуемся предложенной в работах [1, 2] схемой «погружения» линейно упругого тела Q , имеющего кусочно-гладкую границу 5Q , в двусвязную область Q линейно упругого материала с жестко закрепленной внешней dQ' и внутренней 510 , мало отличающейся от dQ поверхностью. Область Q будем рассматривать в качестве нагружающей системы для тела Q . Несмотря на то, что в результате «погружения» поверхности 5Q и 601 совпадают, для более наглядного описания взаимодействия деформируемой и нагружающей систем проведем их мысленное разделение.

Предполагая, что тензоры Грина G ( r , r ' ) и/или Неймана N ( r , r ' ) области (0 известны, дадим следующую формулировку теоремы Клапейрона, которая справедлива для любого распределения напряжений o ( r ) , уравновешенного действительными, определяемыми равенствами (1), внешними поверхностными усилиями S ( r ) , и для любого поля действительных перемещений u ( r ) , соответствующего распределению деформаций е ( г ) .

Теорема. Если в каждой точке r тел Q и £1 справедливы уравнения равновесия в отсутствии массовых сил и геометрические соотношения Коши, то работа номинально заданных поверхностных усилий S ⁰ ( r ) на действительных перемещениях

u ( r ) точек границы d0 , затрачиваемая на создание заданного напряженно-деформированного состояния, определяется соотношением

J S 0 ⁽ r ) u i ⁽ r ) d ^(dQ) = j o ij ⁽ r ) a _y ⁽ r ) d ⁰ + J u i ⁽ r ) J N y ⁽ r , r ') u j ⁽ r ') d ( d^Q ) d ⁽9° ) , (6) 50                   0                50     50

а работа действительных поверхностных усилий S ( r ) на номинально заданных перемещениях u ⁰ ( r ) точек, принадлежащих границе д0 , определяется следующим образом:

J S i ^{( r} ) u i ^{( r} ) d ^(d0) = J ^o ij ^{( r} ) ^a ij ^{( r} ) d ^{0 +} j S i ^{( r} ) J G ij ^{( r} , ^r ') S y ^{( r} ') d ( d⁰ ) d ^(d0) . ⁽⁷⁾ 50                   О                50 dQ

Уравнения (6) и (7) содержат удвоенные значения потенциальной энергии нагружающей системы. Обратим внимание на то, что если при решении краевых задач для тела О характеристики нагружающей системы учитываются локальными граничными условиями контактного типа (3), то из соотношений (6) и (7) следует математическая запись формулировки теоремы Клапейрона, приведенная в работе [1].

Лагранжиан для объединенной механической системы О U 0 при равенстве нулю работы внешних сил на жестко закрепленной границе д0 ' может быть представлен следующим образом:

L = 1 J o ij (r ) a ij (r ) d0 = 1 J Cijmn (r ) a ij (r ) a mn (r ) d0 + J oij (r ) a ij (r ) d0

² 0 U 0                ² L 0                        0

где C ( r ) - тензор модулей упругости. С учетом равенств (2) и (7) второй интеграл в правой части (8), который отражает вклад работы действительных внешних усилий S ( r ) , определяемых соотношением (1), на перемещениях u ⁰ ( r ) - u ( r ) , возникающих при совместной деформации тел 0 и 0 , преобразуется к виду

J oij (r) aij (r) d0 = J [ u (r) - 2ui(r)] Si° (r )d (d0) +

- 0	d0             z А А             .                 (9) + J u i ( r ) J N j ( r , r ) u j ( r ) d (d0) d (d0) . 50     50

Проведем дискретизацию тела 0 и введем для каждого из N ₀ конечного элемента 0_а с 0 вектор степеней свободы { и _а } . Выделим в дискретизованном теле множество узловых точек 0_а , принадлежащих границе 90 . Соответствующие этому множеству степени свободы обозначим { ~ _а} . Пусть [ L _а ] и [ / ,₍,] - матрицы инцидентности, тогда с помощью преобразований

{и а} = [/ а] {U }, {~a}=[La]{U } можно установить связь { иа} и { ~а} с вектором {U}, содержащим глобальные степени свободы дискретизованного тела. В дальнейшем все векторы и матрицы, относящиеся к произвольному элементу 0а , будем отмечать нижним индексом а, а принадлежащие к каждому из N00 конечных элементов, одна из сторон (граней) которых принадлежит границе дискретизованного тела 50 , - волнистой линией.

Пусть решена задача о нахождении симметричной положительно определенной матрицы влияния [ R S ] , устанавливающей связь между силовыми и кинематическими

ˆ

ˆ

величинами во всех узловых точках границы дО области О . Соответствующие этому множеству узловых точек степени свободы дискретизованного тела О обозначим { ~ ° } . Необходимо отметить, что узловые точки тел О и О , принадлежащие поверхностям дО и дО , совпадают, а условное «разделение» границ является вспомогательной операцией для учета характеристик, отражающих взаимодействие деформируемой и нагружающей систем.

Введем логическую матрицу [ H ] , с помощью которой установим связь между векторами { ~ _а } и { ~^ } следующим образом:

{ ~о } [H ][ Фа]{ ~а} .

Заменяя дискретными аналогами слагаемые, входящие в равенства (9) и (10), на основе необходимого условия экстремума лагранжиана объединенной механической системы

( 5 L = 0 ) получим для тела О систему линейных алгебраических уравнений

N П

Е а=1

(                                  )

[Lа] T J [Bа] T [DЛ»а] dО [Lа]

+

V       ^Оа                          )

N b 2

+Е

а= 1

(.

[Lа] J[ Фа] T J_ [H ] [RS ][H]d (an )[фа] d (dO) [lJ

V       ^дОа        5 0                                          )

{U }=

=е fa ^T J [ Ф а ] ^T { S а } d№ ^а = 1 V       дО а                     )

Здесь [ ф_а ] , [ B _а ] и [ D _а ] - матрицы функций формы, градиентов и деформационных характеристик конечного элемента, { S 0 0 } - вектор номинально заданных усилий. Обратим внимание на то, что во втором слагаемом левой части системы (10) внутренний интеграл берется по всей поверхности контакта деформируемого тела и нагружающей системы и содержит информацию о характеристиках области О , в то время как внешний - только по участку границы дискретизованного тела дО , который принадлежит конечному элементу О_а .

Система уравнений (10) может быть представлена в компактной форме

N О

[K ]{ U } = ([K ]+[ K •]){ U } = Е [ Lа] T { Sа} ,(11)

а= 1

NN °°

[K]+[K-] = Е [Lа]Т[Kа][LoHE [l„] [R«][l«], а=1

где [ K ] и [ K _а ] - матрицы узлового ансамбля дискретизованного тела и жесткости конечного элемента соответственно, а [ R _а ] - симметричная положительно определенная матрица характеристик нагружающей системы:

[ R.]= J [ Фа]T J [/H ]T [Rs ][/H]d (asO )[Фа] d (do). 5Оа        д<О

Таким образом, уравнения (11) позволяют учесть нелокальные граничные условия (1) при численном решении краевых задач методом конечных элементов.

Удовлетворение этих граничных условий связано с внесением коэффициентов, определяющих характеристики нагружающей системы, в матрицу узлового ансамбля дискретизованного тела.

Матрица [K'], содержащая характеристики жесткости нагружающей системы, имеет высокую степень разреженности и содержит только ненулевые элементы, которые соответствуют степеням свободы узловых точек, принадлежащих поверхности контакта деформируемого тела и нагружающей системы. В результате конгруэнтных преобразований (11) на этапе построения ансамбля уравнений получаются симметричные матрицы [K] и [K']. Поэтому матрица [K ] узлового ансамбля с удовлетворенными нелокальными граничными условиями (1) также симметрична относительно главной диагонали.

В случае, если влияние нагружающей системы учитывается при решении соответствующей краевой задачи локальными граничными условиями контактного типа (3), выражение (9) может быть представлено в более простой форме [1, 2]

J ° ij ^{( r} ) ^£ ij ^{( r} ) d ^О = J ^[ S i ^{( r} ) u i ^{( r )- 2} S i ° ^{( r} ) u i ^{( r} ) + R j ^{( r} ) u i ^{( r} ) u j ^{( r )]} d ^(5О) .      ⁽¹³⁾

О                5О

При этом условное «разделение» границ 5О и дО (в силу локальности условий) не имеет смысла.

Последовательно заменяя второй интеграл (8) выражением (13) и переходя к дискретным аналогам для слагаемых, входящих в равенства (8) и (13), на основе условия 5 L = 0 получим

N О

X а=1

Г                                    )

[ L а ] T j[ B а ] T [ D а ][ B а ] d О [ L a ]

l       П а                         J

+

N О

+X а=1

(,.„.

ЫT J [Фа] T [R][Фа] d(5О) W l      дПа                           J

Nb

{ U } = X И T J [ ф а ] T { S а } d ( 5О )

а= 1 l

Здесь [ R ] - симметричная положительно определенная матрица характеристик нагружающей системы, известная для каждой узловой точки, принадлежащей границе 50 дискретизованного тела О .

Система линейных алгебраических уравнений (14), являясь частным случаем (10), также может быть представлена в компактной форме (11). При этом матрица характеристик нагружающей системы [ R _а ] конечного элемента О_а , в отличие от (12), будет определена следующим образом:

[ R а ] = J [ Ф а ] ^T [ R ][ Ф а ] d ( 50 ) .                          (15)

5О а

Из уравнений (2) и (5) следует, что для учета на границе 50 заданных без учета сопротивления тела О внешней нагрузке перемещений u ⁰ ( r ) необходимо в подынтегральное выражение, стоящее в правой части (10), сделать подстановку

{ S а } = J [/ / ] T [ R s ] d ( дО ) { u а } ,                            (16)

5О а в подынтегральном выражении правой части (14) вектор {S0°} заменить на

{ s а } = [ r ] { « а } .                                      (17)

Здесь { и а } - вектор номинально заданных перемещений.

При равенстве векторов номинально заданных

{ S О ⁰ } и действительных { S _a }

усилий вторые слагаемые в левой части равенств (10) и (11) отсутствуют, а сами соотношения соответствуют классической системе уравнений метода конечных элементов с удовлетворенными локальными граничными условиями в напряжениях. В другом предельном случае - равенстве номинально заданных {и^ } и действительных {иа} перемещений - из соотношений (16) и (17) следует, что [к] является матрицей узлового ансамбля с удовлетворенными методом подавления кинематическими граничными условиями.

Уравнения (10) обобщают впервые разработанную авторами [8] процедуру учета граничных условий контактного типа (3) при численном решении краевых задач методом конечных элементов. Действительно, если матрица влияния [ R_s ] будет иметь блочное строение и содержать ненулевые локальные коэффициенты жесткости только в симметричных подматрицах, расположенных на главной диагонали, то матрицы характеристик нагружающей системы [ R _а ] , определяемые соотношениями (12) и (15), окажутся эквивалентными. В этом случае ненулевые коэффициенты жесткости будут находиться в позициях, соответствующих степеням свободы узловых точек, принадлежащих границе контакта деформируемого тела и нагружающей системы, и связывать между собой только номинально заданные внешние усилия и возникающие в этих же узловых точках перемещения.

Несложно показать, что наложение дополнительных гипотез, например, возможности представления коэффициентов жесткости R j ( r ) , входящих в граничные условия контактного типа (5), в виде

j) = R(1>S„5U + R<2 >52,82, + Аз i 6з,, как это показано в работе [8], приводит к диагональной матрице [Rа].

Достаточное условие устойчивости деформируемого тела и нагружающей системы. Дадим объединенной механической системе бесконечно малые виртуальные вариации перемещений 6u ( r > , согласующиеся с уравнениями равновесия и кинематическими граничными условиями при би 0 ( г > = 0 . Тогда условие устойчивости объединенной механической системы, соответствующее абсолютному минимуму лагранжиана (9) в положении равновесия ( 8 L = 0), может быть представлено в виде неравенства

J C ijmn ^{( r} > ⁸ ^ ij ^{( r} > ⁸ ^ mn ^{( r} > d ^{O +} J ⁸ ui ^{( r} > J N j ^{( r} , r ' > ⁸ u j ^{( r} ' > d ^(dO > d №) > 0,     ⁽18)

O                           50 SO которое, в случае дискретного представления, эквивалентно требованию положительной определенности матрицы узлового ансамбля [K]. Здесь 5е(г ) -бесконечно малые вариации деформации, вызванные 6u(r) * 0 .

Если характеристики нагружающей системы учитываются при решении соответствующей краевой задачи локальными граничными условиями контактного типа (3), то из неравенства (18) следует условие устойчивости

J Cijmn (r > 8^ ij (r > 8^ mn (r > dn+ J Rij(r > 8 ui (r > 8 uj (r > d (dn)> 0,

O                          50

полученное авторами [1, 2].

Характеристики нагружающих систем однонаправленно армированных композитов и пористых материалов периодической структуры. Для композитов периодической структуры в качестве нагружающей системы (тела Q) может рассматриваться слой типовых элементов, окружающих центральную ячейку [1]. Решение краевой задачи с нелокальными граничными условиями (1) для этого класса материалов может быть получено только в случае, если будут построены граничные тензор-функции Грина или Неймана. Построение этих функций является сложной самостоятельной задачей, решение которой для ограниченных областей заданной геометрии затруднено аналитически, получено только лишь для некоторых, как правило, неограниченных тел. Поэтому особый интерес вызывают методы численного построения матриц влияния [Rs ], являющихся дискретными аналогами граничных тензор-функций Неймана [3].

Одним из способов численного построения матрицы влияния [ R s ] для ограниченной области произвольной геометрии является статическая конденсация [6] (исключение из матрицы жесткости дискретизованного тела Q , рассматриваемого в качестве нагружающей системы, внутренних узловых степеней свободы)

^[ R S ^] = ^{[ K} Ext Ext

^{] - [} K Ext In

][ K In In ] - ' [ K

In Ext

],

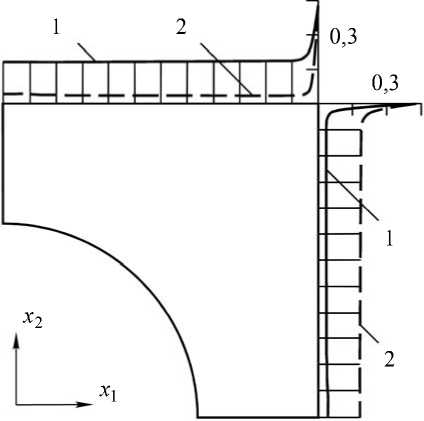
Рис. 1. Распределение локальных коэффициентов жесткости нагружающей системы (108, Н м2 ):

1 – R ₁₁ и 2 – R ₂₂

процедура которой предусмотрена в методе суперэлементов (подструктур) [5, 7]. В выражении (19) индексами In и Ext отмечены коэффициенты, соответствующие внутренним и внешним узловым степеням свободы тела Q . Из равенства (19) следует, что матрица влияния [ R S ] имеет намного меньшую (по сравнению с матрицей жесткости дискретизованного тела) размерность, симметрична и положительно определена. Эта матрица является плотно заполненной, что свидетельствует о наличии нелокальной связи между усилием в некоторой рассматриваемой точке и перемещениями во всех точках границы контакта деформируемого тела и нагружающей системы.

На рис. 1 представлены распределения локальных, находящихся на главной диагонали матрицы [RS ], коэффициентов R 11 и R 22 жесткости нагружающей системы на границах ячейки периодичности композиционного материала тетрагональной структуры с объемной долей туннельных пор vf = 0,3 . Как видим, распределения однородны всюду, за исключением угловой точки, где наблюдается их резкое возрастание. Значения коэффициентов R12 (определяющих вклад перемещения узловой точки в направлении x2 в усилие, возникающее в той же самой точке в направлении x1 ) по сравнению с R11 и R 22 пренебрежимо малы. При построении матрицы влияния объемный и сдвиговой упругие модули матрицы композита предполагались равными Gm = 2,1 ГПа и Km = 3,5 ГПа соответственно, нагружающая система была представлена совокупностью 24126 симплекс-элементов (на границе контакта с центральной ячейкой находилось 89 узловых точек).

Сравнение различных способов учета характеристик нагружающих систем при численном решении краевых задач механики композитов. После построения матриц влияния [RS ] с целью оценки достоверности получаемых результатов были решены краевые задачи о двухосном однородном макродеформировании в поперечной плоскости номинально заданными 811 = 822 = 5,76 -10-3 пористого и волокнистого композитов периодической тетрагональной структуры, в постановке которых нагружающая система учитывалась различными способами: непосредственным включением слоя типовых элементов, окружающих центральную ячейку, в расчетную схему, нелокальными (1) и локальными граничными условиями контактного типа (3).

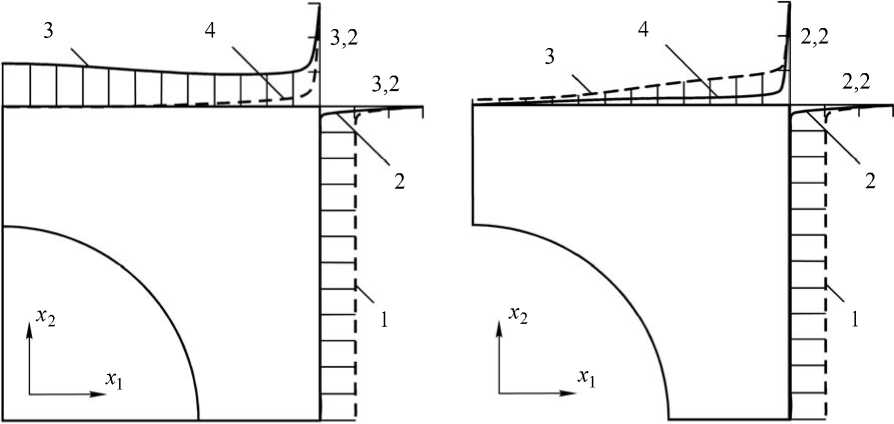
а                                            б

Рис. 2. Распределение реальных усилий S_i ( 10 ⁸ , Н м ) при двухосном однородном макродеформировании однонаправленно армированного волокнистого композита (а) и пористого материала тетрагональной структуры (б) номинально заданными

8 11 = 8 22 = 5,76 - 10 - ³ : граничные условия контактного типа - кривые 1 ( S 1 )

и 2 ( S ₂ ); нелокальные граничные условия – кривые 3 ( S ₂ ) и 4 ( S ₁ )

На рис. 2 показано распределение реальных усилий на границах ячеек периодичности. При выполнении расчетов объемный и сдвиговой упругие модули волокон были выбраны следующими: G f = 10,5 ГПа и K f = 17,5 ГПа. Как и следовало ожидать, при учете только диагональных коэффициентов матрицы влияния законы изменения S_i вдоль границ повторяют соответствующие распределения R ₁₁ и R ₂₂ (см. рис. 1). Кроме того, проведенные исследования показали, что вид распределения значений коэффициентов R ₁₁ и R ₂₂ по границам ячеек периодичности (как следствие, при рассматриваемом способе учета нагружающей системы — реальных усилий S ₁ и S ₂ ) нечувствителен к наличию или отсутствию в матрице жесткого армирующего наполнителя или поры (кривые 1 и 2 на рис. 2), не зависит от их геометрии и объемной доли. Это, прежде всего, может быть объяснено тем, что при замене нелокальных граничных условий (1) локальными условиями контактного типа (3) имеет место неизбежная потеря информации, содержащейся в матрице влияния.

Если в определении реальных усилий участвуют все коэффициенты матрицы влияния [RS ], то характер изменения Si оказывается абсолютно другим (кривые 3 и 4 на рис. 2). Результаты решения краевых задач свидетельствуют о том, что, несмотря на отличие по достигнутым значениям, распределение S1 на верхних границах ячеек периодичности однонаправленно армированного волокнистого композита и пористого материала тетрагональной структуры (кривые 4 на рис. 2) однородно (за исключением угловой точки), качественно повторяет распределение коэффициентов R11 (см. рис. 1).

Вместе с тем изменение усилий S ₂ на границах контакта деформируемой и нагружающей систем имеет ярко выраженный немонотонный характер. Увеличение S ₂ (кривые 3 на рис. 2) наблюдается на участках, наименее удаленных от волокна (см. рис. 2, а) и наиболее удаленных от поры (см. рис. 2, б). Представленные результаты свидетельствуют о том, что матрица влияния содержит интегральную информацию о нагружающей системе: свойствах и геометрии, а также наличии или отсутствии в структуре материала армирующего наполнителя или пор и их объемной доле.

1,10

0,94

0,78

0,62

0,46

0,30

0,30 0,46 0,62 0,78 0,94 1,10

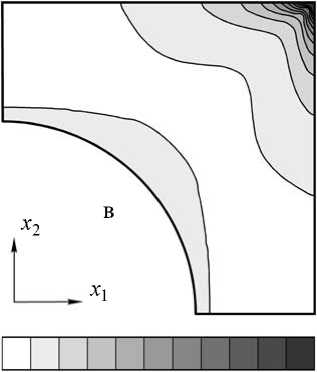
0,00 0,40 0,80 1,20 1,60 2,00

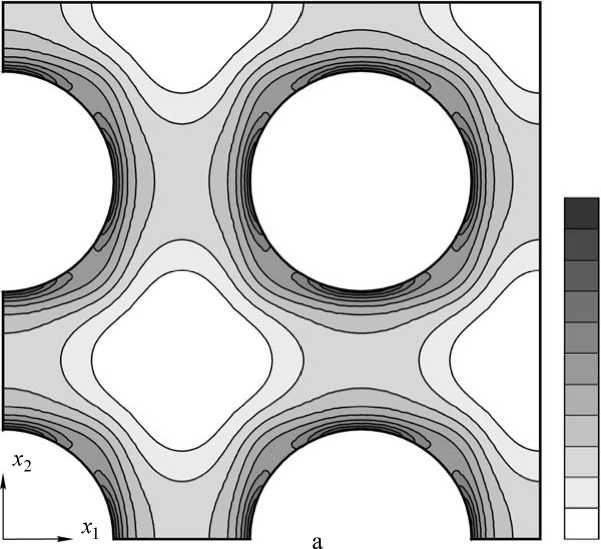
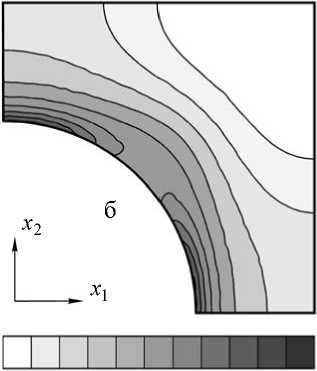
Рис. 3. Изолинии второго инварианта тензора напряжений j^² ) , 10² (МПа) для различных способов учета нагружающей системы

На рис. 3 представлено распределение второго инварианта тензора напряжений j ^ ² ) ( r ) при двухосном однородном макродеформировании в поперечной плоскости композита с объемной долей туннельных пор, равной v f = 0,3. Обращает на себя внимание качественное и количественное совпадение численных решений (см. рис. 3, а и 3, б), полученных в результате непосредственного включения слоя типовых элементов, окружающих центральную ячейку, в расчетную схему и дополнения постановки краевой задачи нелокальными граничными условиями. Для этих двух способов учета нагружающей системы j ^ ² ) ( r ) достигают своих наибольших значений в объемах материала матрицы вблизи свободной поверхности поры.

Характер распределения j ( ² ) ( r ) в случае учета характеристик нагружающей системы граничными условиями контактного типа (см. рис. 3, в) оказывается принципиально иным. Локальный всплеск значений j ^ ^{2 )} ( r ) в угловой точке ячейки периодичности обусловлен (при однородном распределении номинально заданных перемещений на границах) резко возрастающими значениями коэффициентов жесткости R ₁₁ , R ₂₂ (см. рис. 1) и как следствие – реальных усилий S ₁ и S ₂ (см. рис. 2) в этой точке.

Таким образом, численные решения краевых задач для пористых материалов периодической структуры свидетельствуют о корректности разработанной процедуры учета характеристик нагружающей системы нелокальными граничными условиями в методе конечных элементов и показывают, что локальные коэффициенты жесткости не могут в полной мере характеризовать свойства нагружающих систем.

Авторы выражают признательность профессору В.Э. Вильдеману за постоянное внимание к работе и обсуждение полученных результатов.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант РФФИ–Урал № 01–01–96479).