Учет электронных составляющих в уравнении состояния при расчете ударных волн в смеси металлов

Within the framework of additive thermodynamic model of a mixture the electronic components of energy and pressure which make a valuable contribution to the equations of a condition for high temperature processes behind an intensive shock wave are taken into account. The calculations of thermodynamic parameters are fulfilled and the shock adiabat of several mixtures is constructed. A comparison of the calculation results with the experimental data shows a high accuracy of the model (does not exceed shares of percent).

Моделирование распространения ударных волн по многокомпонентным средам представляет в расчетной практике достаточно трудную задачу вследствие невозможности учета влияния всех факторов на физические процессы, происходящие за фронтом ударной волны.

Существует ряд моделей, которыми можно пользоваться для предсказания ударной адиабаты смеси по известным уравнениям состояния ее компонентов. Одно из приближений состоит в том, чтобы, рассматривая смесь как слоистую структуру, рассчитать среднюю скорость ударной волны, основываясь на временах распространения ударной волны через различные слои [1]. Такой способ привлекателен тем, что в данном случае вычисляют характеристику, которая поддается непосредственному измерению. Другая возможность заключается в интерполяции адиабат Гюгонио в координатах (давление - объем) при определенном давлении на основе объемов, занимаемых разными компонентами.

При построении ударных адиабат многокомпонентных сред воспользуемся аддитивной гидродинамической моделью. Будем считать, что размер зерен, составляющих среду веществ, достаточно мал, чтобы структура самой среды смогла оказать влияние на амплитуду ударной волны, распространяющейся по веществу с некоторой скоростью D. Поскольку у такой среды (смеси) отсутствует дефект объема, то ее удельный объем на фронте волны может быть подсчитан как аЧ=т./У1т.’

1=1                            / 1=1         i=1

где V_r удельный объем z-й компоненты при ударном сжатии каждой компоненты по отдельности; Р давление; а, - массовая концентрация; т, - масса z-й компоненты; г, - количество компонент в смеси.

Ударную адиабату среды как смесевой системы будем строить из основного допущения, что при распространении ударной волны по образцу давление во всех компонентах выравнивается, а теплообмена не происходит. В этом случае массовая скорость частиц смеси определятся формулой где U; - массовая скорость т-й компоненты вещества за фронтом ударной волны.

Будем считать, что скорость ударной волны в смеси является линейной функцией массовой скорости смеси, как и для однородного монолита [2], тогда о л2 Гт _I г о    umix I 1 /р . I

^mix " ^mix     mixmix ’ И ^mix                            ‘                      ’ где p.)mn =        , pmix = Уу " начальная и текущая плотности; щшх- обобщенная

'        / ГО mix ‘ "   / '"mix гидродинамическая скорость звука в смеси; Хть - тангенс угла наклона обобщенной прямой в координатах Dmx +Umix- Следуя работе [31. для trulix и Х.™* покутим а.

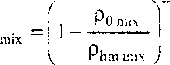
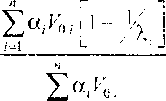
Роп-.ix / . 2 2 уМ Ро i^ai

Таким образом, зная линейную зависимость (2) для каждой из компонент к отдельности, можем получить смесевые константы «щы и X_mi_x, на основании которых построим ударную адиабату Р-Р(Р_т1Х), точную в области, где зависимости для всех компонент смеси Di(Ui) являются линейными. Экспериментальные исследования подтвердили справедливость уравнения Гюгонио на основе линейного закона (2) для умеренных скоростей в случае распространения ударных волн в твердых телах без фазовых переходов, однако оно не дает дополнительной информации о термических свойствах материала. Следует отметить, что ударное нагревание оказывает значительное влияние на ударное сжатие твердых тел. Эти эффекты жу г иып, мной при помощи термодинамического анализа. При использовании подходящей функции энергии теории твердых тел Грюнайзена достаточно для того, чтобы дать полное 1 ермодинамичсское описание поведения и свойств материала при высоких давлениях.

Далее рассматривается термодинамика ударного сжатия. Для идеальной смеси уравнение состояния вдоль изотермы ДДл измеренное при высоких давлениях статическими методами, должно быть точно таким же. какое тает отпитр.лишне объемов, занимаемыми разными компонентами при том же давлении. Для точек на кривой Гюгонио. с другой стороны, это простое смешение несколько усложняется неодинаковым нагреванием компонентов при повышении давления под действием ударной волны. Однако этот эффект мал [4]. если только смешанные вещества термодинамически нс сильно разнятся между собой, но сравнению с энергией, запасаемой каждым из компонентов при сжатии пил действием ударной волны.

Изменение давления вследствие перераспределения энергии из-за такой разницы температур меньше, чем неопределенность в изменении давления, связанная с недостаточными знаниями в поведении коэффициента Грюнайзена при высоких давлениях. С учетом этого обстоятельства расчет в ударной волне смеси проводился упрощенным способом.

Результаты динамических экспериментов устанавливают зависимость удельного объема смеси от давления, и для каждого Р -г- I^z_mix состояния определяют удельною энергию ударного сжатия согласно

Е_Н mix ~Е_{0 mix} = —Р_н (Ро _ппх - Рц.^ ф ^^ai (^i ^- E_Oi^ ^ — Ри^а, (рц . - I , ) , (3) здесь Ен, — удельная энергия /-ой компоненты, приобретенная при ударном сжатии смеси; Ес — начальная удельная энергия.

Условие аддитивности требует дополнительно к уравнению (3) соблюдения почленных равенств, совпадающих с уравнениями Гюгонио отдельных компонент,

При этом, как следует из системы (3, 4), справедливость одного из уравнений (4), одновременно свидетельствует о выполнении при сжатии смеси уравнения Гюгонио и для другого компонента.

Широкодианазонные уравнения состояния [5] достаточно хорошо описывают поведение материалов за фронтом интенсивных ударных волн, однако они содержат большое количество подгоночных параметров, значения которых известны далеко не для всех материалов. Для наших целей выбраны уравнения состояния в форме Ми-Грюнайзена [6]:

Р=Р +

I I ^ѫР, ²

В уравнении (5) присутствуют «электронные» члены, обусловленные тепловым возбуждением электронов, неучет которых при сжатии 8>1,5 приводит к значительным ошибкам при определении температуры, необходимой для фиксации процесса плавления, который для большинства веществ начинается именно в этой области сжатия [2].

В предположении термодинамического равновесия за фронтом ударной волны из адиабат смесей рассчитывались Р^Т диаграммы. Температуру вдоль адиабаты Гюгонио вычисляли по формуле [7]

Тн---

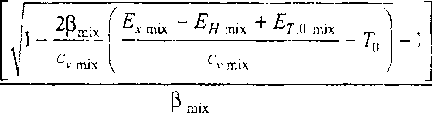
где <у шх - теплоемкость смеси при постоянном объеме; р1Г|Х = (3Л r;„8m^r'/х - коэффициент электронной теплоемкости смеси; у, - электронный аналог коэффициента

Грюнайзена смеси.

Для уравнений, описывающих увеличение энергии с давлением при постоянном объеме, необходимо знать как коэффициент Грюнайзена смеси, так и электронный его т-7г

Необходимо также знать

аналог, или, что равноценно, параметр удельную теплоемкость смеси при постоянном объеме и коэффициент электронной теплоемкости смеси, чтобы привязать адиабату Гюгонио смеси к какой-либо температуре. В нашем случае, согласно [4], предполагали постоянство производной

и удельной теплоемкости компонент. Тогда коэффициент Грюнайзена смеси и его электронный аналог

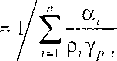
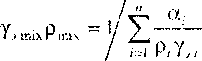
а удельная теплоемкость смеси при постоянном объеме и коэффициент электронной теплоемкости

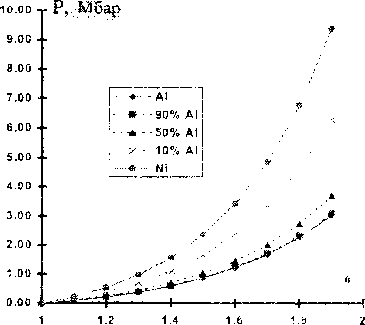
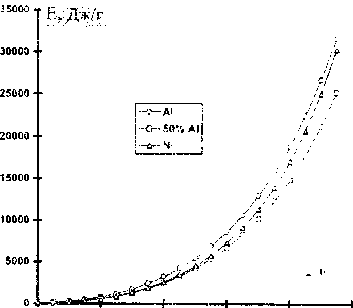
Рис. I. Зависимость давления и удельной энергии от массового состава А1 в (Al-Ni) смеси

На основании вышеизложенного аддитивного подхода были выполнены расчеты термодинамических величин смеси. Так как в литературе нс найдено ни подобных расчетов, ни экспериментальных данных для смесей по отдельным составляющим. то количественное сравнение не производилось. В работе [7] качественно показана зависимость давления и энергии по составляющим («холодная», «тепловая» и «электронная») и их вклад в общее давление, энергию и температуру за фронтом ударной при разном массовом содержании А1 в смеси (Al-Ni), при различных степенях сжатия. Хорошо видно, что ударные адиабаты смесей, а также все составляющие давления и энергии смеси располагаются между' кривыми отдельных компонент, при этом степень приближения кривых смеси к кривым однородных материалов зависит от массовой концентрации компоненты (рис.1.).

На рис. 2. показана зависимость температуры смеси от массового содержания А1 в смеси Al-Ni при нагружении смеси (Al-Ni) алюминиевой пластины со скоростью W=2 км/с. Температура в смеси плавно изменяется от температуры однородного Ni до температуры однородного А1.

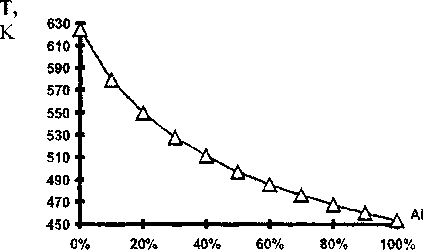
Рис. 2. Зависимость температуры смеси от массового содержания А1 в смеси (Al-Ni)

Количественное сравнение, проведенное по адиабатам сплавов, показывает, что аддитивный принцип расчета нс нарушается. У латуни (весовой состав Си 62,5 %; Zn 37,1 %;РЬ 0,35 %: Fe 0,15%) и железоникелевого сплава (26,2 %, Ni) отклонение прогнозированных кривых от опытных данных в среднем составляет 2-3 % (рис. 3). Сравнение расчетных и опытных данных для этих сплавов показывает, что отклонение не превышает долей процента (кривые практически «ложатся» на экспериментальные точки).

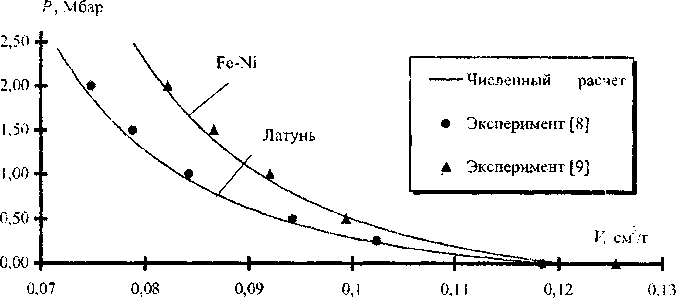
Рис. 3. Сравнение расчетных и экспериментальных данных для сплавов

При определении кривых ударного сжатия сплавов Re-Mo (40,44 Si Мо) и Ti-Мо (25,27 % Мо) применялся расчет, моделирующий метод отражения, подробно изложенный в [2]. На рис. 4. показана зависимость скорости распространения ударной волны от массовой скорости для сплавов Re-Mo, Ti-Mo и сплавов Ni-Cu (50 % Ni). ВНЖ-90 (90 % W, 7 % Ni, 3 % Fe), ВНМ-3-2 (95 % W, 3 % Ni, 2 % Си). На этих рисунках прямые сплавов Ti-Mo. ВНМ-3-2 и их экспериментальные точки условно смещены на единицу вниз по оси D, а у сплава Ni-Cu на единицу вверх по оси D.

• Эксперимент [Ю] Численный расчет

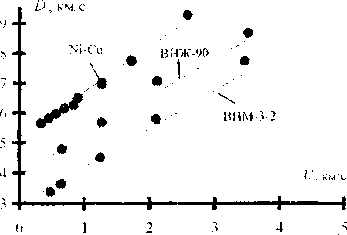
Рис. 4. Сравнение расчетных и экспсримснгальных данных для зависимое in скорости ударной волны от массовой скорост и смеси

• Эксперимент [ Н ]--Численный расчс!

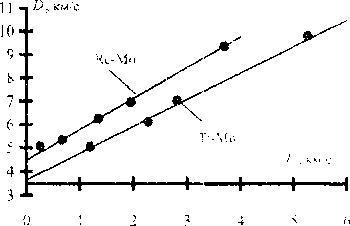
Термодинамическая модель, наряду с хорошей точностью, позволила легко ввести в уравнение состояния «электронные» члены и учитывать их для смеси в целом, а также упрощенным способом построить адиабату' смеси с учетом плавления компонент.

Би бл и о графи чески йен и со к

• 1.    Нестеренко В.Ф., Фомин В.М., Ческидов П.А. Границы применимости моделей поведения порошков при интенсивном ударно-волновом нагружении Л' Численные методы решения задач теории упругости я пластичности: Матер, конф. -Новосибирск, 1988.- С.231 -236.

• 2.    Зельдович Я.Б., Райзер К).II. Физика ударных ноли и выгокотсмлераждных гидродинамических явлений. ■ Мл Наука. Юбб - 688 с.

• 3.    Дидык Р.П. и др. Анализ и расчет динамических параметров в м неч окомпонед : пых соударяющихся средах / Днепропетр. горн. ин-т. - Днепропетровск. 1983. -33 с. -Деп. в ВИНИТИ № 264 Ук-Д84.

• 4.    Мак-Куин Р. и др. Уравнение состояния твердых тел по резуль атам исследований ударных волн // Высокоскоростные ударные явления ; Под pea. B.FI. Николавсского. -М.: Мир, 1973.-С, 299-427

• 5.    Бушман А.В., Ломоносов И.В., Фортов В.Е. Уравнения состояния металлов при высоких плотностях энергий. - Черноголовка, 19*92. - 198с.

• 6.    Фомин В.М., Гулидов А.И., Сапожников Г.А. и др. Высокоскоростное взаимодействие тел. - Новосибирск, 1999. - 600с.

• 7.    Краус Е.И. Моделирование процессов в смесях за фронтом ударных волн: Дис. ... магистра. - Новосибирск, 1998. - 77 с.

• 8.    McQueen R.G., Warsh S.P. Equation of state for nineteen metallic elements from shockwave, measurements to two megabars //Journal of Applied Physics. - 1960. - Vol.31. - N7. - P. 1253-1297.

• 9.    McQueen R.G.. Warsh S.P. Shock-wave compression of iron - nickel alloys and the earth’s core // Journal Geophys. Res. - 1966. - Vol. 71. - N6. - P. 753-797.

• 10.    Жерноклетов M.B., Зубарев B.H., Трунин Р.Ф., Фортов В.Е. Экспериментальные данные по ударной сжимаемости и адиабатическому расширению конденсированных веществ при высоких плотностях энергии. - Черноголовка: ВНИИЭФ, 1996. -388с.

• 11.    Баканова А.А., Дудоладов И.П., Сугулов Ю.Н. Выполнение правила аддитивности для ряда сплавов при ударном сжатии // ПМТФ. - 1972. - № 6. - С. 167-172.

Получено 21.02.2001