Учет корреляционных связей биометрических данных через дробный показатель степеней свободы закона распределения хи-квадрат

В статье рассматривается проблема выбора числа степеней свободы с учетом коррелированности биометрических данных. Показано, что учет корреляции биометрических данных приводит к существенному снижению числа степеней свободы распределения хи-квадрат и дробности показателя размерности.

Безопасность больших и сверхбольших телекоммуникационных систем может быть обеспече- на механизмами дистанционной высоконадежной биометрической аутентификации пользователей [1]. Очевидно, что стойкость высоконадежной дистанционной биометрической защиты к атакам подбора должна быть проверена на реальных статистических данных. Для сокращения статистик необходимо знать вид закона распределения значений биометрических данных [2]. Например, гипотеза о том или ином законе распределения значений может быть проверена по критерию хи-квадрат [3].

Обычно при проверке гипотезы того или иного распределения значений предполагается, что статистические данные независимы. К сожалению, это не всегда так и, зачастую, обрабатываемые биометрические статистические данные оказываются зависимы (коррелированны). В частности стандарт [1] допускает наличие парных корреляционных связей между выходами преобразователя биометрия-код на уровне ±0,15. Как будет показано ниже наличие столь существенной корреляционной связи в биометрических данных должно учитываться, так как приводит с существенному сокращению показателя эквивалентного числа степеней свободы распределения хи-квадрат.

На рис. 1 представлены графики хи-квадрат распределения для различного числа степеней свободы ( m ). Из рисунка видно, что вид плотности распределения существенно зависит от выбора значения m . Чем больше число степеней свободы, тем больше стандартное отклонение полученного распределения и тем сильнее смещается центр распределения вправо.

Так как полностью независимые биометрические параметры на практике не встречаются, необходимо осуществлять учет наличия корреляционных связей. При использовании классического хи-квадрат распределения корреляцию обычно не учитывают. Для упрощения процедуры учета корреляционных связей необходимо осуществить нормирование значений хи-квадрат по числу степеней свободы.

Рис. 1. Плотность классического хи-квадрат распределения для различного числа степеней свободы

Плотность хи-квадрат распределения после осуществления процедуры нормировки представлена на рис. 2. Как видно из рисунка при увеличении числа m происходит уменьшение стандартного отклонения распределения, и математическое ожидание стремится к единице.

Рис. 2 – Плотность нормированного хи-квадрат распределения для различного числа степеней свободы

На рис. 3 приведена зависимость стандартного отклонения распределения от числа степеней свободы нормированного хи-квадрат распределения для идеальных некоррелированных данных, которая описывается следующим соотношением:

2 т (m) = —=

m

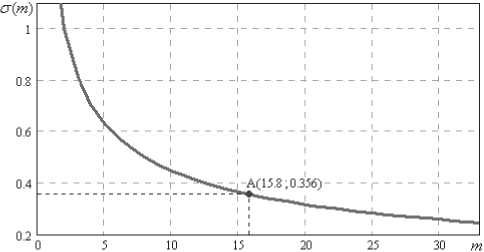
Рис. 3. График зависимости стандартного отклонения от числа степеней свободы нормированного хи-квадрат распределения

Так как реальные биометрические данные обладают существенной корреляционной связью, ее влияние необходимо оценивать. Для этой цели использовалась методика создания вектора равнокореллированных данных подробно изложенная в [2]. По этой методике были смоделированы 2; 4; 8; 16; 32 и 64-х мерные векторы с плавно изменяющейся корреляционной связью от 0,0 до 0,9.

В случае независимых данных, когда корреляция равна нулю, значение стандартного отклонения нормированного хи-квадрат распределения легко вычислимо аналитически (1) и хорошо совпадает с результатами численного эксперимента. Увеличение внутренних корреляционных связей в каждом из векторов, приводит к росту стандартного отклонения нормиро- ванного хи-квадрат распределения. В пределе при r ^ 1 имеет место о(m) ^ V2 для всех m.

Связь стандартного отклонения и коэффициента корреляции приведена на номограмме (рис.4).

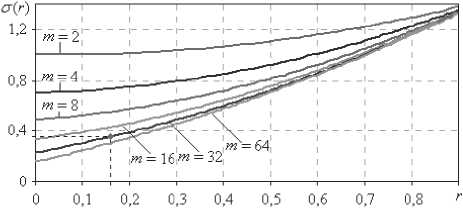
Рис. 4. График зависимости стандартного отклонения от корреляции и числа степеней свободы для нормированного хи-квадрат распределения

Аппроксимация полиномом второй степени экспериментально полученных данных дает приемлемую точность. Соответствующие полиномы приведены в таблице 1.

Для числа степеней свободы, равного 128; 256;, 512 и т.д. связь стандартного отклонения и корреляции становится практически линейной. В случае, когда r ^ 1 для любого количества степеней свободы стандартное отклонение примет единственное значение s = V2 . При больших значениях числа степеней свободы номограмма зависимости стандартного отклонения от значения коэффициента корреляции линейна и строится всего по двум точкам. Значение ^σ для нулевой корреляции рассчитывается по формуле (1), а в точке единичной корреляции ^σ постоянно и не зависит от m .

Таблица 1. Аппроксимация семейства кривых рис. 4

m	7 ( m )
2	0,534 r 2 – 0,061 r + 1,007
4	0,700 r 2 + 0,103 r + 0,700
8	0,745 r 2 + 0,285 r + 0,487
16	0,698 r 2 + 0,491 r + 0,336
32	0,592 r 2 + 0,697 r + 0,228
64	0,504 r 2 + 0,853 r + 0,156

Приведенные выше рис. 3-4 позволяют учесть влияние коэффициентов корреляции на параметры соответствующего нормированного распределения хи-квадрат.

Для примера рассмотрим закон нормированного распределения хи-квадрат с 32 степенями свободы. Пусть исходные данные будут иметь коэффициент корреляции 0,16. По номограмме рис. 4 значению r = 0,16 для кривой m = 32 соответствует стандартное отклонение равное 0,356 (на рис. 3 помечено точкой).

Интуитивнопонятно,что увеличениезначения коэффициентов корреляции эквивалентно снижению числа степеней свободы или эквивалентной размерности моделируемого вектора. В частности при полной коррелированности данных (корреляция 1) число степеней свободы должно упасть с 32 до 1.

Для учета данного эффекта воспользуемся графиком рис. 3. По номограмме рисунка найденное значение стандартного отклонения 0,356 соответствует дробному показателю числа степеней свободы равному 15,8 (точка А на графике). Округлим дробный показатель числа степеней свободы 15,8 до ближайшего целого числа – 16. Это означает, что, оценивая вероятность той или иной гипотезы по критерию нормированного хи-квадрат, вместо 32 степеней свободы, мы должны использовать только 16. Иными словами показатель числа степеней свободы упал в 2 раза. Что не позволяет использовать классические таблицы значений хи-квадрат распределения при оценке коррелированных данных, из-за появления существенной методической ошибки.

Выходом в данной ситуации является использование таблиц нормированного хи-квадрат распределения (таблица 2). Данная таблица получена путём деления значений классической таблицы хи-квадрат на число степеней свободы. Пользуясь таблицей 2, можно для каждого значения нормированного хи-квадрат распределения и числа степеней свободы найти вероятность справедливости той или иной гипотезы.

Для использования на практике описанного выше подхода учета влияния коэффициента корреляции на фактическое количество степеней свободы рассматриваемого распределения необходимо вначале вычислить среднюю по модулю корреляцию [2] рассматриваемых данных. Далее имея вычисленную среднюю по модулю корреляцию и, зная количество степеней свободы по номограмме рис. 4, определяют стандартное отклонение. Для нахождения фактического количества степеней свободы необходимо воспользоваться номограммой рис. 3 или формулой (1). В дальнейшем для полученного числа степеней свободы рекомендуется использовать значения таблицы 2.

В приведенном выше примере получился дробный показатель числа степеней свободы (15,8).Не-обходимо отметить, что в связи с дискретностью шага m таблица 2дает приближенный результат в

Таблица 2. Значения нормированного хи-квадрат в зависимости от m и p

p m	0,95	0,90	0,80	0,70	0,50	0,30	0,20	0,10	0,05
2	0,037	0,091	0,216	0,373	0,700	1,197	1,584	2,192	2,774
4	0,160	0,264	0,390	0,539	0,848	1,259	1,539	2,017	2,404
6	0,260	0,347	0,488	0,608	0,888	1,215	1,468	1,757	2,036
8	0,345	0,453	0,592	0,711	0,966	1,233	1,418	1,718	1,997
10	0,407	0,511	0,639	0,751	0,954	1,185	1,351	1,637	1,852
12	0,443	0,528	0,641	0,752	0,944	1,170	1,336	1,554	1,789
14	0,486	0,571	0,680	0,770	0,948	1,164	1,290	1,495	1,695
16	0,488	0,567	0,691	0,791	0,974	1,157	1,272	1,440	1,617
18	0,496	0,600	0,719	0,817	0,967	1,161	1,281	1,481	1,645
20	0,558	0,631	0,732	0,814	0,978	1,157	1,269	1,449	1,593
22	0,583	0,644	0,753	0,832	0,983	1,148	1,263	1,406	1,553
24	0,578	0,644	0,741	0,831	0,966	1,127	1,252	1,413	1,526
26	0,602	0,672	0,756	0,828	0,971	1,113	1,205	1,362	1,471
28	0,598	0,666	0,769	0,835	0,969	1,122	1,219	1,349	1,473
30	0,603	0,683	0,786	0,848	0,981	1,117	1,213	1,358	1,474
32	0,633	0,698	0,781	0,852	0,982	1,103	1,201	1,352	1,437

Таблица 3. Детализация значения нормированного хи-квадрат в зависимости от m и p

p m	0,95	0,90	0,80	0,70	0,50	0,30	0,20	0,10	0,05
15	0,467	0,568	0,693	0,785	0,943	1,133	1,244	1,456	1,658
15,2	0,471	0,568	0,693	0,786	0,949	1,138	1,250	1,453	1,650
15,4	0,475	0,568	0,692	0,787	0,955	1,143	1,255	1,450	1,642
15,6	0,480	0,567	0,692	0,789	0,962	1,147	1,261	1,446	1,633
15,8	0,484	0,567	0,691	0,790	0,968	1,152	1,266	1,443	1,625
16	0,488	0,567	0,691	0,791	0,974	1,157	1,272	1,440	1,617

случае дробного показателя m из-за отсутствия промежуточных значений. Выходом в таком случае является рассмотрение значений для ближайших целых показателей степени и интерполяция исходных данных с шагом 0,2.В нашем случае интерполяции подвергаются значения для m=15 и m=16 . Результаты интерполяции данных таблицы 2 приведены в таблице 3.

Для более точного учета нужна дальнейшая интерполяция данных таблицы 3.

Описанные выше проблемы корректировки ас-симетричного хи-квадрат распределения актуальны только для относительно низких размерностей. Для большого числа степеней свободы (128; 256; 512; 1024) закон нормированного хи-квадрат распределения становится практически нормальным – математическое ожидание для которого равно 1,а стандартное отклонение рассчитывается по формуле (1). Следовательно,для больших степеней свободы рекомендуется переходить к нормальному закону распределения с легко вычислимым математическим ожиданием и стандартным отклонением.

В заключении следует еще раз подчеркнуть, что наличие корреляционных связей висходных данных приводит к существенной методической погрешности при использовании классического хи-квадрат распределения. Для ее исключения необходимо переходить от целой (дискретной) размерности числа степеней свободы идеального распределения хи-квадрат к эквивалентному распределению зависимых данных с существенно меньшим дробным (фрактальным)показателем степеней свободы реальных зависимых биометрических данных.