Учет краевых эффектов при определении рабочего магнитного потока в микродвигателях с постоянными магнитами с помощью метода конечных элементов

Цитирование: Солдатов А. В. Учет краевых эффектов при определении рабочего магнитного потока в микродвигателях с постоянными магнитами с помощью метода конечных элементов / А. В. Солдатов, С. Н. Афанасьев // Журн. Сиб. федер. ун-та. Техника и технологии, 2025, 18(7). С. 962–970. EDN: QTDLLK

Проблема заключается в том, что при аналитическом расчете и решении магнитной и электромагнитной задач в двумерной постановке рабочую длину индуктора, создающего рабочий магнитный поток, приравнивают к реальной длине индуктора, пренебрегая краевыми эффектами, за счет которых указанные длины не равны друг другу, что приводит к неточному определению рабочего магнитного потока и, следовательно, к неточному прогнозированию рабочих характеристик проектируемого электродвигателя.

В данной работе установлен коэффициент, учитывающий краевые эффекты от индуктора электродвигателя. Для этого была построена модель магнитной системы электродвигателя в трехмерной постановке, выполненная в программном комплексе Ansys Maxwell, и приведены зависимости магнитной индукции от геометрии магнитной системы.

В качестве объекта исследования рассмотрена магнитная система двухполюсных коллекторных и бесколлекторных электродвигателей постоянного тока беспазового исполнения с постоянными магнитами для следящих систем.

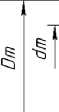
Модель магнитной системы электродвигателя в двумерной осесимметричной постановке представлена на рис. 1.

Lm

Lk

Рис. 1. Модель магнитной системы электродвигателя: h _k – толщина спинки магнитопровода; δ – толщина воздушного зазора; D _m – внешний диаметр постоянного магнита; d _m – внутренний диаметр постоянного магнита; L _m – аксиальная длина постоянного магнита

Fig. 1. Model of the magnetic system of the electric motor: h _k – lamps of the back of the magnetic circuit; δ – air gap; D _m – outer diameter of the permanent magnet; d _m – inner diameter of the permanent magnet; L _m – axial length of the permanent magnet

В результате численного моделирования магнитной системы электродвигателя в трехмерной постановке получим график распределения магнитной индукции по длине корпуса L _k (по оси Х, мм) и длине окружности L , радиус которой равен среднему значению между внешним диаметром D _m постоянного магнита и внутренним диаметром корпуса. Графики представлены на рис. 2.

Рабочий магнитный поток рассчитывается по классической формуле

Фδ = BδMAX · α · τ · Lm,

где B δMAX – максимальное значение магнитной индукции в воздушном зазоре; α – коэффициент полюсного перекрытия в диапазоне 0,6–0,8; τ – полюсное деление.

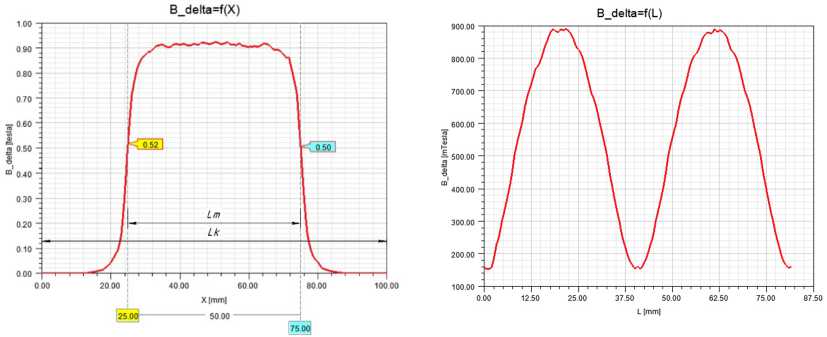
Исходя из рис. 2б, коэффициент полюсного перекрытия α равен 0,635383 (≈ ).

аб

Рис. 2. Распределение магнитной индукции: а – по длине корпуса L k ; б – по длине окружности L

Fig. 2. Distribution of magnetic induction: a – along the length of the housing L _k; б – along the length of the circumference L

По рис. 2 а видно, что магнитная индукция, приближаясь от середины до края постоянного магнита, начинает резко падать примерно до значения (0,45–0,48) · B _δMAX. Магнитная индукция от края постоянного магнита до края корпуса резко падает до нуля.

На рис. 3 представлены зависимости магнитной индукции от геометрии магнитной системы электродвигателя.

При B δ = f ( L k ) отношение менялось в диапазоне 1…2. При увеличении длины корпуса

L _k относительно длины магнита L _m индукция в теле корпуса изменялась от 2,3 до 1,5 Т, за счет чего индукция в магнитном зазоре росла до определенного значения, ограниченного МДС воздушного зазора. При минимальной длине корпуса L k магнитная система уходит в насыщение, магнитная проницаемость магнитопровода в зоне максимальной концентрации индукции падает и, следовательно, растет магнитное сопротивление магнитопровода. За счет этого магнитный поток устремляется к менее насыщенным участкам корпуса. Поэтому в зоне минимальной индукции, перпендикулярной вектору намагничивания, при насыщении концентрируются повышенные значения магнитной индукции в воздушном зазоре электродвигателя, которые могут быть больше индукции по направлению вектора намагничивания постоянных магнитов.

При B _δ = f ( h _k) толщина спинки магнитопровода h _k менялась в диапазоне 1…4,25 мм. Индукция менялась от 2,6 до 1,5 Т. Картина распределения индукции в воздушном зазоре аналогична зависимости B δ = f ( L k ).

Зависимость B _δ = f ( L _b) аналогична зависимости B _δ = f ( L _k).

При B δ = f ( δ ) толщина воздушного зазора δ менялась в диапазоне 0,25…4. При росте толщины воздушного зазора МДС воздушного зазора растет, что требует от постоянных магнитов повышенного МДС. За счет этого рабочая индукция постоянного магнита смещается вниз по кривой размагничивания, тем самым магнитная индукция воздушного зазора падает. Следует учесть, что при минимальном воздушном зазоре его МДС минимальна, достигается максимальное рабочее значение магнитной индукции постоянного магнита, что, в свою очередь, – 965 –

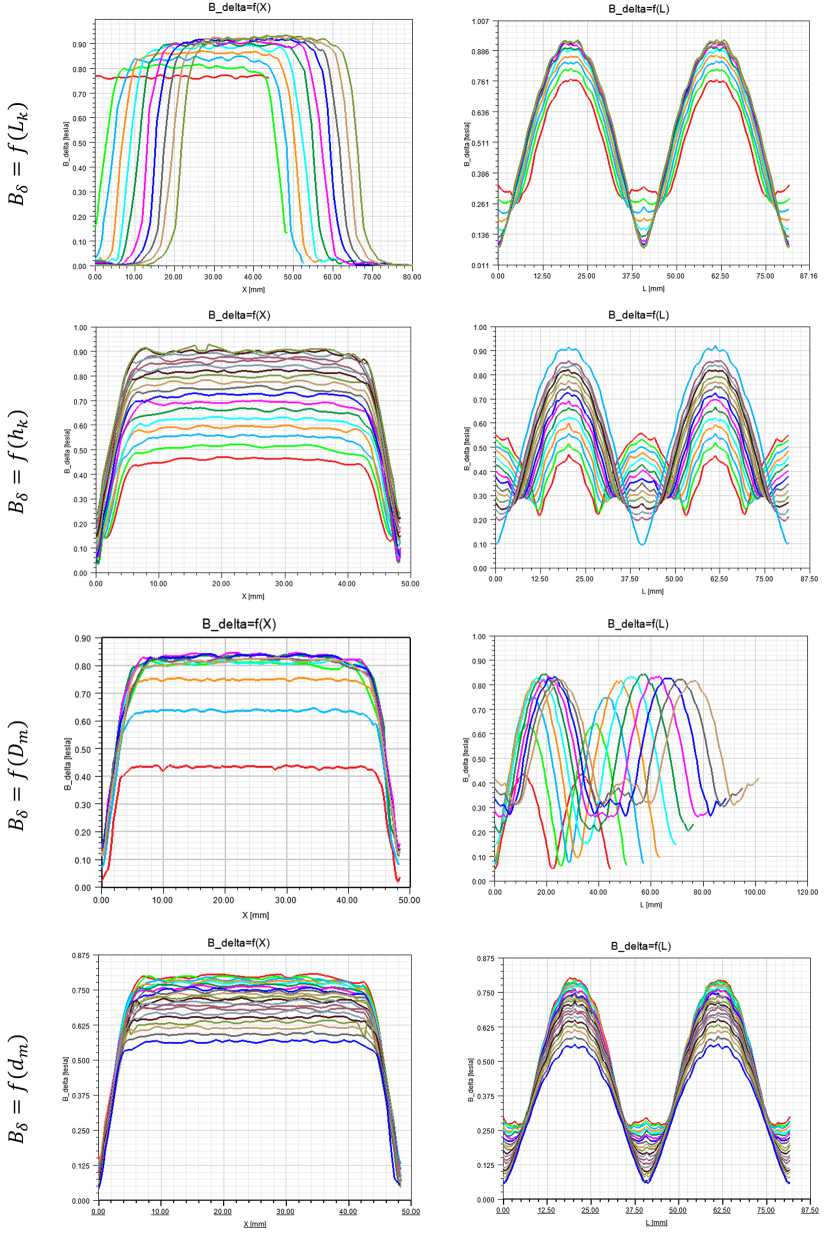
Рис. 3. Зависимость магнитной индукции B _δ = f ( L _k, h _k, D _m, d _m, δ , L _m)

Fig. 3. Dependence of magnetic induction B _δ = f ( L _k, h _k, D _m, d _m, δ , L _m)

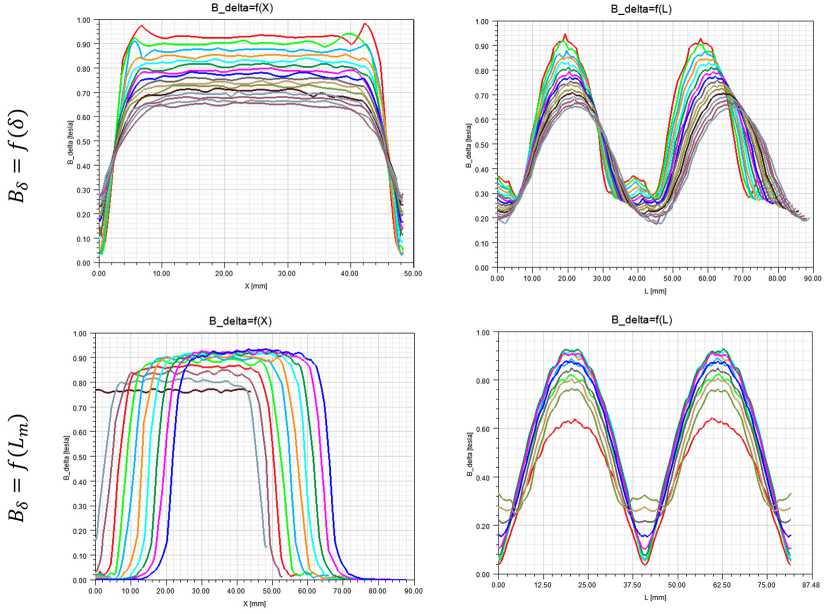
Рис. 3. Продолжение

Fig. 3. Continued может привести к насыщению магнитопровода. Поэтому минимальное значение индукции в воздушном зазоре становится больше.

При B _δ = f ( D _m) диаметр D _m меняется в диапазоне 1…10. При увеличении внешнего диаметра магнита D m растут магнитные индукции в воздушном зазоре и в теле корпуса. Затем корпус насыщается, постоянному магниту требуется больше МДС, чтобы скомпенсировать МДС корпуса. За счет этого магнитная индукция в воздушном зазоре сначала растет, затем падает, ограничиваясь МДС корпуса.

При B δ = f ( d m ) диаметр d m меняется в диапазоне 1…6. При увеличении внутреннего диаметра магнита d _m растут магнитные потоки рассеивания. За счет этого основной магнитный поток падает. Таким образом, магнитная индукция воздушного зазора падает.

На рис. 4 представлена зависимость коэффициента полюсного перекрытия от геометрии магнитной системы (количество точек N в выборке).

На рис. 4 имеются точки, которые дальше всех отдалены от остальных. Эти точки получены при насыщенном магнитопроводе. Поэтому эти точки можно не учитывать. Таким образом, среднее значение коэффициента полюсного перекрытия α составляет 0,63. Относительная по- грешность по отношению к менее 1,05 %. Результаты показали, что коэффициент полюсного п

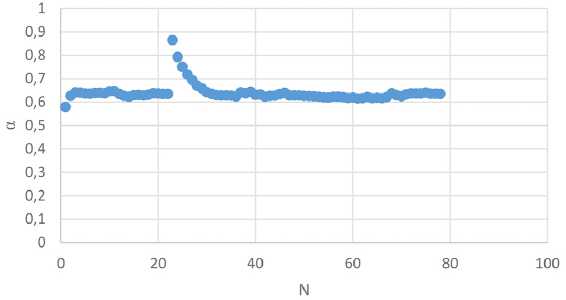
Рис. 4. Зависимость коэффициента полюсного перекрытия α = f ( L _k, h _k, D _m, d _m, δ , L _m)

Fig. 4. Dependence of the pole overlap coefficient α = f ( L _k, h _k, D _m, d _m, δ , L _m)

перекрытия не зависит от магнитной системы электродвигателя, а зависит лишь от формы индуктора, в нашем случае от постоянного магнита, при условии, что магнитная цепь находится в ненасыщенном состоянии.

На основании рис. 3 (графиков распределения магнитной индукции по длине корпуса)

Ф'5

найдены удельные магнитные потоки    (удельный магнитный поток на единицу длины по- люсной дуги, Вб/м) по длине обмотки LОБМ = (1,1–1,4) · Lm без учета лобовых частей для коллекторных электродвигателей с полым якорем и бесколлекторных электродвигателей с гладким статором с помощью метода трапеций по формуле:

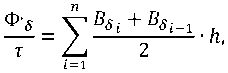
где i – номер текущего интервала; n – количество интервалов (трапеций); B δ _i – значение индукции в воздушном зазоре в текущем интервале, Тл; B_{δi –1} – значение индукции в воздушном зазоре в предыдущем интервале, Тл; h – ширина интервала (от общей длины обмотки без учета лобовых частей), мм.

По результатам расчетов выведены отношения между реальным удельным магнит- ным потоком с учетом краевого эффекта и расчетным удельным магнитным потоком

Фд

Т

®<5СР ‘ ^

в виде коэффициента краевого эффекта. На рис. 5 представлена зависимость коэффициента краевого эффекта от геометрии магнитной системы (количество точек N в выборке).

На рис. 5 имеются точки, которые дальше всех отдалены от остальных. Эти точки получены при насыщенном магнитопроводе. Поэтому эти точки можно не учитывать. Таким образом, коэффициент краевого эффекта k КЭ находится в диапазоне 0,96…0,98. Результаты показали, – 968 –

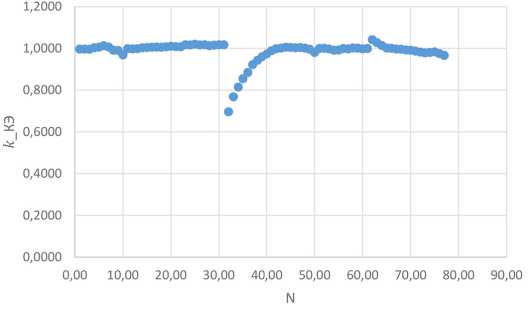
Рис. 5. Зависимость коэффициента краевого эффекта k _КЭ = f ( L _k, h _k, D _m, d _m, δ , L _m)

Fig. 5. Dependence of the coefficient of the edge effect k _КЭ = f ( L _k, h _k, D _m, d _m, δ , L _m)

что коэффициент краевого эффекта слабо зависит от магнитной системы электродвигателя при условии, что магнитная цепь находится в ненасыщенном состоянии.

Уточненная формула для определения рабочего магнитного потока с учетом краевого эффекта:

Ф _δ = k _КЭ · B _δMAX · α · τ · L _m.                                                     (3)

Заключение

В результате проделанной работы получен коэффициент, учитывающий краевые эффекты от постоянного магнита в двухполюсных коллекторных и бесколлекторных электродвигателях.

Полученные результаты позволят ускорить инженерные аналитические расчеты и процессы моделирования в двумерной постановке с сохранением требуемой точности по сравнению с трудоемким и долгим моделированием в трехмерной постановке.