Учет пластических деформаций при колебаниях балки

Необходимость решения задач динамики систем с разрушающимися связями за пределами упругости появляется при расчете строительных конструкций и инженерных сооружений на прогрессирующее обрушение [1]. Аналитические решения в данной области могут быть получены для ограниченного класса задач, вследствие чего часто применяются численные методы моделирования.

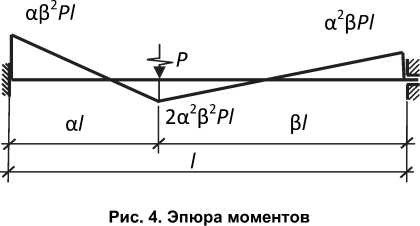
С целью учета пластических деформаций рассмотрим жестко защемленную металлическую балку, в которой при динамической нагрузке разрушается угловая связь. На рис. 1 показана расчетная схема балки до разрушения жесткого защемления (угловой связи) и после разрушения. Жесткое защемление балки обеспечивается болтами М24 класса прочности 8.8, материал болтов – сталь 35Х (рис. 2). На рис. 3 показаны диаграмма деформирования стали 35Х (кривая 1) и полученная на ее основе билинейная диаграмма деформирования, состоящая из двух линейных участков (кривая 2). Под действием нагрузки, прикладываемой ближе к левой опоре (рис. 4), разрушается ряд болтов, вследствие чего жесткое защемление преобразуется в шарнирное опирание.

Задачами исследования являются следующие. На основе диаграммы деформирования стали болтов определить параметры билинейной диаграммы в координатах «усилие – перемещение». Построить математические модели упругопластического

Рис. 1. Расчетная схема балки: а) исходная схема, б) после разрушения угловой связи расчета поврежденной балки. Проведение численной реализации временного анализа балки на действие динамической нагрузки с учетом пластических деформаций при разрушении жестко защемленной опоры.

Математические модели. Следуя традиционной схеме, представим уравнение движения системы с нелинейной восстанавливающей силой в следующем виде [2]:

MY(t) + CY(t) + R(t) = P(t) (1) где M = diag ( m 1 , ... , m n ), C = C T – матрицы масс и демпфирования; Y ( t ), R ( t ), P ( t ) - векторы перемещений, динамических восстанавливающих сил и внешней нагрузки.

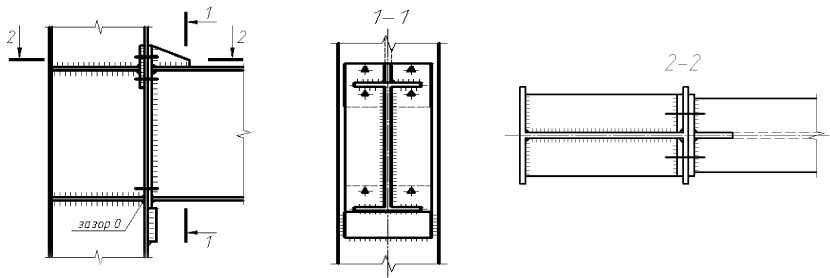
Рис. 2. Схема рамного узла

Теория расчета строительных конструкций

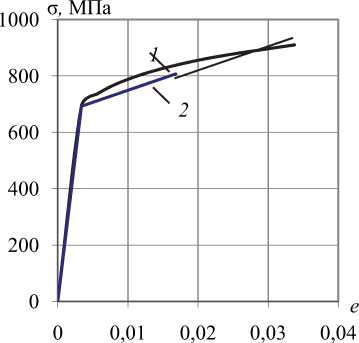
Рис. 3. Диаграммы деформирования:

1 – исходная диаграмма, 2 – билинейная диаграмма

Полагаем, что жесткость болтового соединения изображается зависимостью R~у «восстанавливающая сила - относительное перемещение» на основе билинейной диаграммы (рис. 5). Согласно приведенной диаграмме, вектор динамических восстанавливающих сил имеет упругую R e (наклонная линия с углом а), упругопластическую составляющую R _пл (наклонная линия с углом а₁) и составляющая остаточных усилий R (наклонная линия параллельная первоначальной линии).

Пусть от начала действия внешней нагрузки и до некоторого момента времени t1, соединение на высокопрочных болтах работает упруго, тогда векторы восстанавливающих сил Re(t) и переме щений Y(t) связаны линейной зависимостью Re(t) = K(ti)Y(t), где K(ti) - положительно определенная матрица жесткости балки в момент времени ti [2].

Предположим, что при t > 1 1 под действием динамической нагрузки в соединении достигается состояние текучести, зависимость между векторами R ( t ) и Y ( t ) становится нелинейной. Эта нелинейность связана с появлением в момент времени t i вектора предельных значений R_np ( t i ) = A K(t i )Y ( t i ), где A K(t i )= Kt - 1 )-K(t)

В последующие моменты времени в связи с достижением в несущем элементе максимальных перемещений рост пластических деформаций прекращается, наступает разгрузка, и система снова возвращается к упругой работе. На этапе разгрузки вектор восстанавливающих сил помимо упругой и предельной составляющих имеет составляющую в виде вектора остаточных усилий R ( t i ) = K(t i )Y_p ( t ).

Таким образом, вектор динамических восстанавливающих сил на интервале времени ( t i , t i ₊₁) имеет вид

R(t)=Re(t) + Rnp(t{)-R*(tO. (2)

После подстановки (2) в левую часть выражения (1) и преобразования уравнение движения ква-зиупругой системы на интервале времени t е [ t i , t i ₊₁] ( i = 0, 1, ...) имеет вид

MY(t) + CY(t) + K(tl)Y(t) =

= P(t)-Rnp(tO + R*(t{).

Данное уравнение позволяет свести неупругий анализ дискретной диссипативной системы к последовательности расчета квазиупругих систем, изменяющихся в фиксированных временных точках t i ( i = 1, 2, ...). Квазиупругие решения на каждом интервале времени ( t i , t i ₊₁) строятся в форме, аналогичной интегралу Дюамеля, выведенному для упругой системы [2].

Алгоритм работы системы. При сложных динамических воздействиях система может испытывать многоцикловое деформирование. На рис. 6 показан гистерезисный характер деформирования болтов рамного (жесткого) узла балки. При работе материала болтов в упругопластической стадии

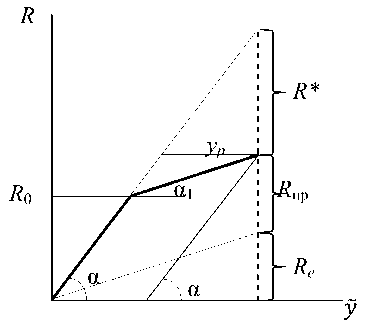
Рис. 5. Зависимость «восстанавливающая сила – перемещение»

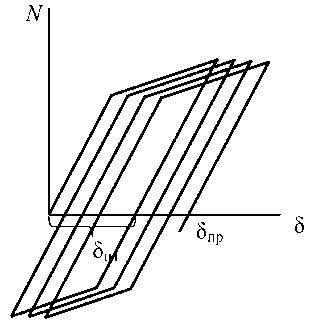
Рис. 6. Гистерезисная диаграмма жесткости болтов

Лемберг Е.В.

Учет пластических деформаций при колебаниях балки происходит накопление пластических деформаций вследствие необратимых искажений структуры [3]. Условием разрыва болтов является достижение суммарных пластических деформаций предельного значения δпл ≥δпр . В результате разрушения ряда болтов жестко защемленный опорный узел балки переходит в шарнирное закрепление.

Выводы. На основе теории временного анализа предложен алгоритм упругопластического расчета металлической балки как дискретной диссипативной системы. Алгоритм позволяет строить в аналитическом виде динамическую реакцию системы с нелинейной восстанавливающей силой при многоцикловом характере деформирования. Открывается возможность получения оценок по конструктивной безопасности конструкций.

Материалы подготовлены по тезисам доклада на 5-й научной конференции аспирантов и докторантов ЮУрГУ.