Учет реальных условий опирания пролетных строений в создании их конечно-элементной модели

Постановка вопроса на первый взгляд может показаться несколько наивной при том, что практика мостового строительства не отличается большим разнообразием конструктивных форм опорных частей и в большинстве случаев для реализации конечно–элементной модели необходимо и достаточно задать привычный вариант опирания пролетного строения.

На примере пролетного строения разрезной системы считается корректным принять опирание на шарнирно–неподвижную одним концом и шарнирно–подвижную опорную часть другим концом пролета. Подобная схема опирания является обычной в адекватном отражении разрезного пролетного строения.

В аналогичном порядке, как правило, представляют условия опирания в случае использования распространенных в мостовом строительстве резино–металлических опорных частей (РОЧ), что дает основание для утверждения о существовании системы и ее работоспособности.

В то же время конечное значение вертикальной и горизонтальной (сдвиговой) жесткости РОЧ инициирует соответствующее отражение их упругой податливости в расчетной схеме. Покажем, что эта инициатива не лишена смысла. Пусть для балки, опертой концами на РОЧ с вертикальной С в и сдвиговой С г жесткостью при симметричном загружении как единственно неизвестная горизонтальная реакция F = X i может быть найдена из канонического уравнения метода сил:

5 11 X 1 + A lp = 0

На рисунке 1 представлены схема балки, схема ее нагружения, расчетная схема на основе стержневой аналогии, основная система.

При постоянной изгибной EJ и нормальной EA жесткости балки и с учетом симметрии схемы балки и ее нагружения оценка перемещений в направлении неизвестного Х 1 возможна интегрированием деформаций на половине длины балки. В таком случае коэффициент при неизвестном δ 11 и свободный член Δ 1p будут равны:

0,5L0,5

511 = — J Mx 1 Mx 1 dx +    J Nx 1 Nx 1 dx + 7г-(2)

EJ 0             EA 0

• 1    0 , 5 L

Alp =-EJ J MPMX1dx(3)

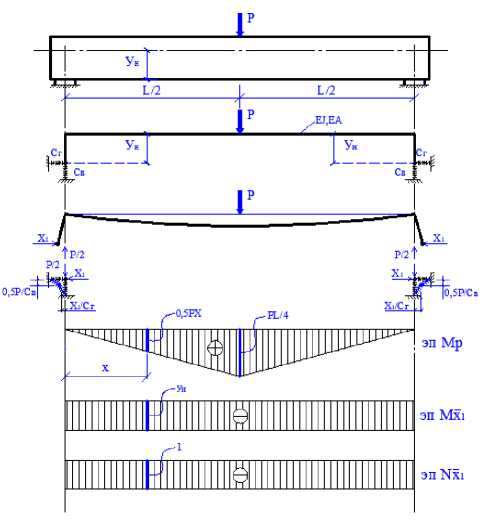
Рисунок 1

Выражение δ 11 характеризует перемещение в направлении действия неизвестной горизонтальной реакции Х 1 = 1, которая формирует:

• -    в балке изгибающий момент M _Х1 = у_н и продольное сжимающее усилие N х 1 = 1;

• -    сдвиговые смещения в РОЧ с площадью горизонтального сечения А р , модулем сдвига резины G p суммарной высотой резиновых прослоек h p , обуславливающих сдвиговую жесткость C_r=A_pG p /h p .

Выражение Δ 1р отражает перемещение балки в основной системе в уровне опирания в направлении действия неизвестной горизонтальной реакции от действия внешней силы Р , вызывающий момент М_р= 0,5 Рх.

С учетом обозначенных величин M _Х1, N _Х1, М р , С г :

= yu +_ L _+ h ;

¹¹   2 EJ 2 EA G p A p

A --Рун^-

^1p     16 EJ "

С подстановкой (4) и (5) в уравнение (1) определяется неизвестная горизонтальная реакция F=X 1 :

F = PyHK КyHL + _L_ + hp ) .

16 EJ / ( 2 EJ 2 EA G p A p J

При заданной схеме нагружения сосредоточенной силой P , с учетом найденной горизонтальной реакции F и вертикальной жесткости опорной части С в прогиб балки в середине пролета находится из выражения

0,5l0, f = —  MMdx - —   FyHMdx +^^P.(7)

EJ J0 p p EA J0    H p      Св

В выражении (7):

M _p =0,5 x - изгибающий момент от вертикальной единичной силы, приложенной в середине пролета;

Св = А р Е р /h - вертикальная жесткость опорной части с площадью горизонтального сечения А р , модулем упругости опорной части Ер и общей высотой h .

С раскрытием M _p, С_в выражение (7) приобретает вид

PL ³ FL ²      0,5 Ph

---У И +-- -48 EJ 8 EJ H E p A p

При действии силы Р единичного значения Р=1 вертикальное перемещение по линии ее действия составит где

r L FL     0,5 h f =---У H +--,

48 EJ 8 EJ ^H E_pA_p

У н ^

F =     16 EJ yH L + L + hp

2 EJ 2 EA G_pA_p

-

Уместно отметить, что принятая форма стержневой аналогии в виде жестких вставок по осям балки и жестко соединенного с ними на уровне нейтральной оси горизонтального стержня с жесткостями EJ и EA способствует ясности представления взаимодействия балки и опорных частей и направления перемещений в уровне их контакта-

Полученные выражения (6), (8), (9), (10) характеризуют работу балки при действии сосредоточенной силы P в середине пролета- Вместе с тем эти выражения, очевидно, могут быть использованы для характеристики колебательного процесса сосредоточенной массы m=P/g в середине пролета невесомой балки с круговой частотой to и периодом Т свободных колебаний, равных

ГТ-

Ю =     ’ mf

Ю

В случае равномерно распределенной массы по длине пролета выражения (11), (12) остаются справедливыми, если массу пролетного строения весом Q сосредоточить в середине пролета со значением m прив.

17 Q

---• — -

35 g

по мнению С.П. Тимошенко [1], адекватно отражающим влияние распределенных масс на параметры колебательного процесса.

В качестве примера рассматривается пешеходное пролетное строение [2] с расчетным пролетом L =42,0 м с поперечным сечением несущей структуры на рисунке 2 и жесткостными параметрами EJ=5,376∙10 ⁵тс∙м², EA=2,470∙10⁶ тс.

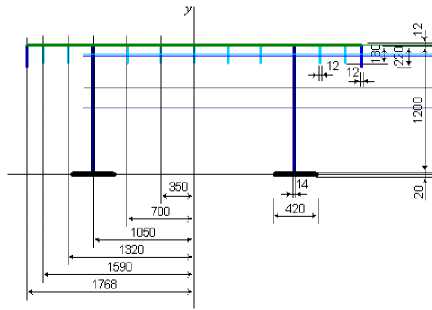
Рисунок2

Постоянные нагрузки с учетом собственного веса несущих металлоконструкций, покрытия проходной части, ограждающих конструкций и остекления составили q=1,599 тс/м .

Каждая из балок пролетного строения обоими концами опирается на резиновые опорные части РОЧ 30х40х7.8 - 1.0 с применением резины НО-68-1, для которых с учетом конструктивных параметров по данным [3] и расчетных положений [4] значения жесткостей составили:

горизонтальной сдвиговой

C =

вертикальной

C г

G p A p

= 360 тс / м ;

h p

E А

= ^^ = 6,725 ■ 10⁴ тс / м .

h

С учетом обозначенных исходных данных, принимая во внимание две опорные части на каждой опоре при двубалочной структуре, при Р=- кгс получены: горизонтальная реакция по (10) прогиб от единичной силы по (9)

значение приведенной массы по (13)

круговая частота по (11)

период свободных колебаний по (12)

F = 0,122 кгс ; f = 2,832d0 ^-4 см; т= 33,295 кгс-с²/см; го =10,299 с^- ;

Т= 0,610 с .

а

б

в

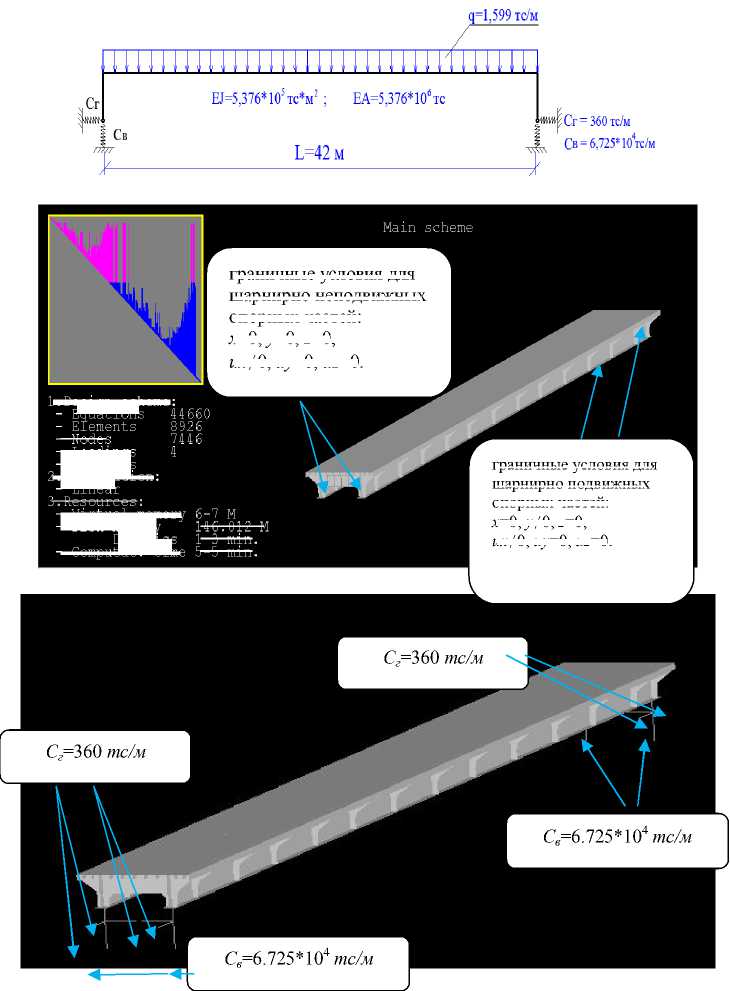
146.012 И граничные условия для шарнирно неподвижных опорных частей:

х=0, у=0, z=0, uxФ0, uy=0, uz=0.

граничные условия для шарнирно подвижных опорных частей:

х=0, уФ 0, z=0, uxФ0, uy=0, uz=0.

- Nodes s. Reson roes:

Рис.3. Варианты конечно-элементной модели пролетного строения

- Loadings

- Dynamics

• 2 .Computation:

• -    Virtual memory

• -    Disk memory Dynamics

• -    Uomputat. time

  1-3 min.

  
  
  
  

Отметим, что при классической схеме опирания (на шарнирно-неподвижную одним концом и шарнирно-подвижную другим) пролетного строения и соответствующем обнулении второго и третьего слагаемых в выражении (9) получено

• / = 2 , 871 - 10 ^-4 см ; to = 10 , 230 с^-1; T = 0 , 614 с .                           (15)

Далее, для сопоставления с аналитическими решениями рассмотрены реализованные в ПК Лире 9.2 конечно-элементные модели (КЭМ) (рис. 3).

Для пролетного строения, представленного плоской стержневой КЭМ с соответствующими ранее рассмотренному примеру жесткостями (рис. 3а), решение в ПК Лира 9.2 дало to = 10,197 с 1; T = 0, 616 с.                                    (16)

Решение пространственной КЭМ пролетного строения, в котором ортотропная плита, стенка балок, нижние пояса, продольные и поперечные ребра представлены оболочечными элементами с их общим количеством 8926 (рис. 3 б,в ), дало результаты:

при опирании по варианту на рисунке 3б пролетное строение имеет первую форму колебаний в вертикальной плоскости с параметрами to = 10, 085 с-1; T = 0, 623 с;(17)

при опирании пролетного строения на резиновые опорные части по схеме на рисунке 3в колебательный процесс пролетного строения характеризуется низшей формой, проявляющейся в крутильных колебаниях с параметрами to = 10,173 с-1; T = 0, 618 с,(18)

колебаниями по второй форме в вертикальной плоскости с круговой частотой и периодом to = 10, 639 с-1; T = 0, 591 с.(19)

Полученные данные позволяют отметить следующее.

Учет жесткостных характеристик резиновых опорных частей вскрывает хотя и упругоподатливую, но дополнительную связь, повышающую жесткость системы в целом. Это находит отражение в сопоставлении результатов аналитических решений по (14) и (15). Аналогичное соотношение отмечается в численных решениях по (16) и (17).

Как в аналитических, так и в численных решениях различие результатов невелико и, как обычно говорят в таких случаях, сопоставимо с погрешностью вычислений.

Не акцентируя на возможностях метода конечных элементов в оценке анализируемых параметров на пространственной конечно-элементной модели пролетного строения, отметим: сопоставление решений КЭМ пролетных строений с условиями опирания по схемам на рисунке 3 б и 3 в устанавливает их влияние на формирование колебательного процесса и величину периода колебаний в вертикальной плоскости: период колебаний Т=0,623 с по (17) и Т=0,591 с по (19).

Можно и в этом случае говорить о малом различии анализируемых величин. Однако, касаясь конкретного объекта [2], нужно отметить, что детализация условий опирания в плане адаптации конечноэлементной модели к результатам испытаний пролетного строения привела к уменьшению периода вертикальных колебаний (Т=0,623с по (17) и Т=0,591с по (19)), величина которого оказалась в пределах интервала, запрещенного нормативными документами.

Таким образом, полученые аналитические зависимости позволяют провести анализ влияния де-формативных свойств резиновых опорных частей на жесткостные характеристики пролетных строений, а приведенные численные примеры подтвердили необходимость отражения реальных условий опирания в создании конечно-элементной модели пролетных строений при обосновании их проектных решений.