Учет релятивистского эффекта в имитаторах спутниковых радионавигационных систем

Цитирование: Сушкин, И. Н. Учет релятивистского эффекта в имитаторах спутниковых радионавигационных систем / И. Н. Сушкин, В. А. Копылов, Р. А. Руф, Д. Е. Коршунов // Журн. Сиб. федер. ун-та. Техника и технологии, 2021, 14(7). С. 854–859. DOI: 10.17516/1999-494X-0351

от i -го НКА до НАП; т i, tr - задержка распространения сигнала в тропосферном слое Земли от i -го НКА до НАП; VTi, s – отклонение часов i -го НКА от часов Центрального синхронизатора; т i, rec — задержка распространения сигнала приемного тракта НАП; Ri, ef - корректировка псевдодальности, вызванная гравитационным и релятивистским эффектом.

Для учета поправочного коэффициента псевдодальности, обусловленного релятивистским эффектом, необходимо произвести коррекцию часов навигационного космического аппарата.

В соответствии с интерфейсным контрольным документом ГЛОНАСС [3] для описания ухода шкалы времени бортовых часов НКА A TS(t ) относительно времени Центрального синхронизатора Т цС ( / ) принята математическая модель нестабильности в виде дифференциального уравнения

WMM№^^^ ,                  (2)

где A f ( t ) - относительное отклонение частоты бортового генератора от генератора Центрального синхронизатора; 5(t ) - долговременная составляющая нестабильности генератора на интервале времени не менее одного часа; ω( t ) – кратковременная составляющая нестабильности генератора; Frel ( t ) - нестабильность, вызванная гравитационным и релятивистским эффектом.

В дискретном виде уход шкалы времени VT(tk) на интервале времени t е [ tk , t_{k +1}] представляется равенством

ТпT+i kT(tkJ=kT(tk) + s(ty(t-tk) + J o)(T)dr+ J F^dT.(3)

△Й0 = Нт^-^^ h = t^x-tk.(4)

4+i— 4

Долговременная составляющая нестабильности бортового генератора s ( t ) представляется гладкой функцией, допускающей параметрическое разложение в той или иной системе базисных функций [4]. Как правило, долговременную составляющую нестабильности частоты хорошо описывают модели полиномиального типа. Кратковременная составляющая нестабильности бортового генератора ω( t ) представляется в виде выходного сигнала фильтра, на входе которого действует «белый шум» с ограниченной дисперсией.

Для уравнения (1) долговременная составляющая нестабильности s(t) представляется на интервале времени [tk, tk+1] линейной комбинацией s^-^^tya^F^tY

z=0

где ф_i(t ) - базисные функции; ai - неизвестные постоянные на интервале времени [ tk , tk ₊₁], которые подлежат оцениванию для каждого типа генератора. В качестве базисных функций применим ортогональный полином Чебышева, для расчета которых применяются следующие выражения:

Ф o ( t ) = 1,

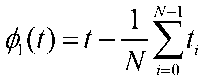
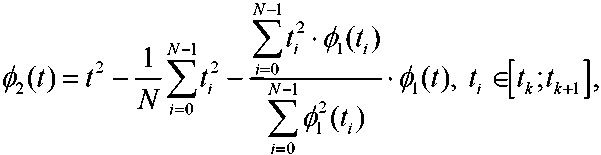
где N — число измерений на интервале [tk , tk +1 ].

При аппроксимации дискретных значений исследуемого процесса с помощью полиномов Чебышева можно перейти к степенным полиномам. При этом выражение (1) будет иметь вид

5(0 = a_s0 + a_$1(t_k+1 -t_kyt^a_s2 • &₊₁ - t_kY + F_rei(t), t e[o₊₁ -t_k\ (6)

При этом коэффициенты разложения a i пересчитываются в коэффициенты степенных полиномов asi и имеют следующий смысл:

• —    as о — смещение шкал времени;

• —    as 1 — относительное отклонение частот;

• —    as ₂ — дрейф частоты на интервале [ tk , tk ₊₁].

Значения коэффициентов asi передаются навигационным космическим аппаратом в качестве частотно-временных поправок (ЧВП).

При применении имитационных систем для проверки работоспособности, отработке алгоритмов и программного обеспечения, а также поверки метрологических характеристик навигационной аппаратуры потребителя ставится задача учета релятивистских эффектов. Причинами этих эффектов являются гравитационное поле Земли и его неоднородность, гравитационные поля соседних небесных тел, неравномерность вращения Земли, высокие скорости измерителей и др. Уровень относительных релятивистских измерений интервалов времени, расстояний и частоты электромагнитных волн в околоземном пространстве достигает 10-9-1010, что на 5—6 порядков превышает достигнутые на сегодняшний день относительные инструментальные погрешности эталонов времени и частоты [5].

Релятивистская составляющая F_rel(t ) нестабильности частоты из уравнения (1) вызвана влиянием изменяющегося гравитационного поля Земли. Значения уходов часов

Jr,,(rW=AT,„+AT                                  (7)

tk где VTcon – постоянное смещение часов, зависящее от величины главной полуоси орбиты НКА, и равно около 37 мкс/сут [3]; VTi — периодическое смещение шкалы времени, зависящее от параметров движения НКА (эксцентриситета, угловой аномалии, главной полуоси орбиты).

Релятивистский эффект является причиной замедления хода бортовых часов. Принято разделять для ГНСС две составляющие:

• 1)    Постоянная составлявшая, представляет собой смещение частоты, компенсируется как пропорциональное смещение частоты для всех опорных генераторов ГЛОНАСС Vf / f = -4,36 • 10^-10 и для GPS V f / f = -4,47 • 10^-10 согласно интерфейсным контрольным документам. Эта поправка незначительно изменяется от спутника к спутнику, так как зависит от главной полуоси орбиты, служащей причиной смещения часом наблюдаемого НКА.

• 2)    Периодическая составляющая, которая в основном зависит от эксцентриситета орбиты, в равной степени соответствует общим и специальным релятивистским эффектам (откло-

• нение высоты и скорости НКА от средних значений). Величина специального релятивистского эффекта (обусловленная средней скоростью НКА) обычно включается в постоянную часть.

Общепринятая периодическая погрешность, применяемая всеми потребителями высокоточных GPS, рассчитывается как

• 2 /—-—

М^рег = —- Ja-GM -e-sinE ,                                    (8)

с где a– большая полуось эллипсоида Земли; e – эксцентриситет; E – эксцентрическая (угловая) аномалия орбиты спутника GPS; c – скорость света; G – гравитационная постоянная; M – масса Земли.

Движущиеся бортовые часы спутника со временем T_sv связаны с номинальной шкалой времени системы ГЛОНАСС преобразованием, полученным согласно общей теории относительности,

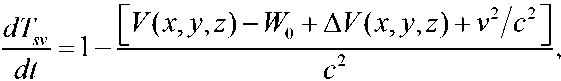
где V – гравитационные и приливные потенциалы Земли; Δ V – гравитационные и приливные потенциалы из-за Луны и Солнца в точке НКА с координатами ( x , y, z ) и скоростью движения v ; W₀ — потенциал геоида от среднего уровня моря, является константой и эквивалентен среднему радиусу Земли R = GM / W ₀.

В уравнении (9) гравитационный потенциал Земли описывается как

V^y^GMlr-R,(10)

где r – радиус орбиты спутника; R – потенциал возмущения, определяемый как

_ Е ( 3

R = GM——sin zcos2z/ + -sin г — L(11)

г3 Ч 4            42/ где i и и — отклонение орбит и аргумента широты и = (го + f), т. е. сумма истинной аномалии f и угла перигея w.

Квадрат скорости движения НКА можно определить отношением Кеплеровских орбит движения v2 =GM(l/r-l/a)

После интегрирования (9) получаем абсолютную релятивистскую временную поправку t = Tsv - ^ =1^-™^!/^ + ^ [1/2ц - 2/r + R/GM - A K/GM^ dt^. (13)

На уровне пикосекунд потенциалом прилива Луны, Солнца и других планет А К ( x , y , z ) можно пренебречь.

Наиболее значительные возмущения орбит навигационных космических аппаратов ГЛОНАСС вызывается влиянием второй зональной гармоникой J ₂. Следующие наиболее значительные возмущения на порядок меньше и возникают в результате притяжения Солнца и Луны. Остальные возмущения орбит спутников еще более меньшего порядка, чем от Солнца и Луны.

Вывод. При формировании псевдодальности в имитаторе спутниковых радионавигационных сигналов ГЛОНАСС для наиболее точной проверки работоспособности навигационной аппаратуры потребителя и отладки высокоточных алгоритмов обработки радионавигационных сигналов необходимо вносить поправочный коэффициент, обусловленный релятивистским эффектом, который может достигать единиц метров. Данный поправочный коэффициент формируется для каждого навигационного космического аппарата.