Учет статической устойчивости синхронных генераторов в задаче планирования оптимальных режимов собственных электростанций по реактивной мощности

В связи с увеличением доли объектов собственной генерации крупных промышленных предприятий в покрытии их суммарной нагрузки вопросы обеспечения устойчивой работы и качества электрической энергии за счет собственных мощностей становятся более актуальными. Традиционно, собственные генераторы рассматриваются как источники активной мощности. Оптимизация режимов сетей производится также по активной мощности с учетом различных критериев оптимальности: минимума затрат на топливо, потерь электроэнергии и т. д. Это оправдано тем, что оплата реактивной мощности и энергии потребителями не производится. Основными требованиями, предъявляемыми к электроэнергетическим объектам, являются надежность, экономичность и качество электрической энергии. Экономичность работы сетей, как правило, предусматривает ведение режимов, оптимальных по различным критериям. Одним из основных критериев является минимум потерь активной мощности. Поскольку эти потери в значительной мере определяются передаваемой реактивной мощностью, то экономически целесообразное ее распределение между объектами соб- ственной генерации с целью снижения потерь является актуальным. Запас статической устойчивости синхронной машины определяет возможность работы синхронного генератора при заданной реактивной мощности. На величину выдаваемой реактивной мощности влияет величина реактивных нагрузок, подключенных к шинам генераторного напряжения. Диапазон их изменения, как правило, известен. При этом встает задача определения оптимальных параметров режима для заданного диапазона реактивных нагрузок при соблюдении ограничений по статической устойчивости. Зависимость запаса устойчивости от текущего режима определяет комплексный характер задачи.

Постановка задачи

Вопросы оптимизации параметров режима по активной мощности изложены в большом числе трудов отечественных и зарубежных ученых. Авторы [1–5] первоочередное внимание уделяют особенностям моделирования заводских тепловых электростанций с поперечными технологическими связями в задаче оптимизации режима. В [1, 2] рассмотрена реализация метода динамического программирования применительно к системам электроснабжения крупных промышленных предприятий, располагающих несколькими собственными электростанциями с разнородным технологическим оборудованием и сложными расходными характеристиками. Получение экономико-математических моделей турбогенераторов промышленных электростанций, работающих на нескольких видах топлива, в том числе вторичных газах металлургического производства, рассмотрено в [3–5]. Подход, предложенный в этих работах, позволяет использовать уравнения связи и целевые функции любого вида, но учет ограничений на зависимые параметры режима (токовые нагрузки элементов сети, узловые напряжения, показатели статической устойчивости и т. д.) представляет определенную сложность. Авторы [6] отмечают возрастающую важность учета режима собственных электростанций активных потребителей при планировании графика нагрузки энергосистемы и взаимодействия таких потребителей с энергоснабжающими организациями. Математический аппарат оптимизации режимов электроэнергетических систем совершенствуется во многом в направлении использования активно-адаптивных устройств. Так, в работе [7] предложен подход, основанный на использовании дробно-полиномиальных зависимостей параметров режима от параметров схем замещения элементов системы и направленный на упрощение моделирования и повышение вычислительной эффективности в условиях задач большой размерности. Ряд работ (например, [8]) посвящен автоматическому управлению генерацией.

Исследованием вопросов устойчивости энергосистем и систем электроснабжения также занималось большое число ученых. Вопросы анализа статической и динамической устойчивости рассмотрены в работах зарубежных ученых [9–16]. В статье [9] указывается важность устойчивости работы энергосистемы, ее классификация, характеристики, приводится ряд технических мероприятий по улучшению статической и динамической устойчивости и их экономическое обоснование в целом. Вопросы исследования нарушения устойчивости из-за внезапного увеличения мощности нагрузки изложены в [10]. Для поддержания устойчивости системы в этом случае одной из задач является определение оптимального местоположения регулятора FACTS, а также вычисление величины напряжения и угла, который будет подан в систему. Предлагается гибридный метод для определения оптимального местоположения регулятора FACTS, а также для вычисления величины напряжения и угла, который должен быть введен в систему, чтобы поддерживать стабильность системы. В работе [11] изложены вопросы повышения динамической устойчивости энергосистем с использованием статического компенсатора VAR (SVC), управляемого искусственной нейронной сетью (ANN). Вспомогательные управляющие сигналы для SVC играют очень важную роль в смягчении электромеханических низкочастотных колебаний ротора. Регулирование параметров осуществляется на основе искусственной нейронной сети с учетом отклонения скорости генератора. В статье [12] производится анализ моментов затухания спонтанных колебаний энергосистемы, встречающиеся на очень низких частотах, с использованием линеаризованной модели малых возмущений и ее применение обобщено на многомашинные энергосистемы для динамической оценки режимной надежности. Статья [13] описывает применение программы анализа переходных процессов ETAP для моделирования энергосистем с целью анализа переходных процессов. В этом труде описывается полная имитационная модель энергосистемы с учетом паровых, газовых и гидротурбинных генераторов и протяженных линий электропередачи. Производится подробный анализ переходных процессов и статической устойчивости многомашинной системы при наличии и отсутствии систем автоматического регулирования возбуждения синхронных генераторов. В работе [14] описывается интеллектуальная система (IS), использующая синхронные векторные измерения для оценки устойчивости переходных процессов (TSA). Для TSA после нарушения одной из основных проблем является время отклика, которое в литературе приводится как фиксированное значение в диапазоне до 3 с после устранения неисправности. В этой статье разработана новая IS, чтобы сбалансировать требования к скорости и точности отклика. Автоадаптивный механизм принятия решений TSA предназначен для постепенной регулировки времени отклика, так что IS может выполнять классификацию быстрее, тем самым оставляя больше времени для аварийного контроля. В статье [15] исследуется детальный гибкий подход для включения различных гибких регуляторов систем передачи переменного тока (FACTS) в среду с многомашинной системой электропитания для улучшения устойчивости энергосистемы. Целью данной статьи является разработка общей методологии модели энергосистемы DAE с включением последовательных и шунтирующих регуляторов FACTS в индивидуальном и скоординированном режиме управления для улучшения устойчивости многомашинной энергосистемы. Статья [16] посвящена вращающемуся конденсатору с регулируемой скоростью, способному регулировать не только реактивную, но и активную мощность, что обеспечивает повышение устойчивости энергосистемы. Таким образом, исследования зарубежных ученых, направленные на повышение как статической, так и динамической устойчивости преимущественно с использованием дополнительных регулирующих устройств, не учитывают возможной оптимизации загрузки источников по реактивной мощности и ориентиро- вания на крупные энергосистемы, работающие с электрически удаленной нагрузкой.

Среди отечественных ученых такие вопросы также неоднократно изучались [17–22]. Вопросы анализа статической устойчивости синхронных генераторов в электроэнергетических системах с учетом статических характеристик нагрузки изложены в трудах [17, 22]. Анализу статической и динамической устойчивости генераторов местных электростанций, в том числе возможности выхода на раздельную работу и последующей ресинхронизации, посвящены труды [18, 19, 21]. В данных работах для анализа устойчивости промышленных генераторов используется программный комплекс «КАТРАН», в основу которого положены методы последовательного эквивалентирования, динамического программирования, последовательного утяжеления и последовательных интервалов.

Как показывает обзор, реализация желаемых режимов возможна при комплексном подходе к вопросам планирования режимов и неизбежно требует коррекции законов автоматического регулирования возбуждения.

В рамках данной работы предполагается определение оптимальных реактивных мощностей промышленных синхронных генераторов в условиях изменяющихся реактивных нагрузок на генераторном напряжении, работы генераторов по электрическому графику, обеспечения минимума потерь при необходимом запасе статической устойчивости.

Теоретическая часть

В связи с изложенным в настоящее время возникает ряд вопросов, связанных с управлением потоками реактивной мощности в промышленных узлах сложной конфигурации, имеющих большое количество собственных источников электроэнергии. Один из таких вопросов – оптимальное распределение потоков реактивной мощности по критерию минимума затрат на потери активной мощности за счет передачи реактивной – связан с экономичностью энергохозяйства предприятия. Для решения задачи оптимального распределения активной и реактивной мощности между источниками электроэнергии предлагается использовать метод динамического программирования в сочетании с методом последовательного эквивалентирования [1, 2]. При решении задачи оптимизации должны учитываться ограничения в форме равенств, определяющих баланс активной мощности в системе электроснабжения, и ограничения в форме неравенств, отражающих располагаемую мощность агрегатов.

Разработан алгоритм (рис. 1), позволяющий определить оптимальный режим работы собственной электростанции по реактивной мощности. Для расчета установившегося режима применен модифицированный метод последовательного эквива- лентирования, позволяющий в сочетании с методом динамического программирования в прямом ходе определить набор оптимальных решений задачи распределения реактивных мощностей в пределах располагаемой мощности генерирующих источников. Условия связи с энергосистемой задаются на границе раздела и обеспечивают выполнение балансовых условий, а следовательно, и выбор единственного оптимального решения. Преимущество использования последовательного эквивален-тирования заключается в том, что в соответствии с принципом оптимальности на каждом шаге эквива-лентирования определяется оптимальный план решения только между двумя переменными, что значительно сокращает объём вычислений.

В общем виде задачу оптимизации можно сформулировать следующим образом: найти минимум целевой функции:

n

F = X ЗД Q j^ min                (1)

i = 1

при ограничениях:

Q i min ^ Q i ^ Q i max ;

X Q i - X q j = Q bx .

Для оценки режима по показателям статической устойчивости необходим также учет ограничений по активной мощности:

p

i min i i max ;

X P i — X P j = Рвх.

В выражениях (2) и (3) P i , Q i – активная и реактивная мощности генератора i ; P вх , Q вх – входная активная и реактивная мощности связи с энергосистемой; p j , q j – активная и реактивная мощности нагрузки.

Учитывая разнообразный характер технико- экономических характеристик генераторов, желательно применять алгоритм, позволяющий использовать функции затрат любого вида, которые могут иметь нелинейности, разрывы и другие свойства, а также могут быть заданы табличными числовыми значениями [3, 4].

Функция (1) представляет собой стоимость активных потерь, обусловленных выработкой реактивной мощности, и имеет вид квадратичной зависимости:

3 i ( Q i ) = C i ( a i Q i + b i Q i ) , (4) где a i , b i – коэффициенты, учитывающие технические данные машины и ее системы возбуждения; C – стоимость единицы потерь активной мощности.

Функция (4) должна быть представлена в виде табличной зависимости с выбранным шагом с учётом максимально возможной и минимально возможной величины реактивной нагрузки генератора.

В условиях заводских электрических сетей 110–220 кВ малой протяженности вводится допущение, что все генераторы являются подключенными к одному узлу. Получение эквивалентной

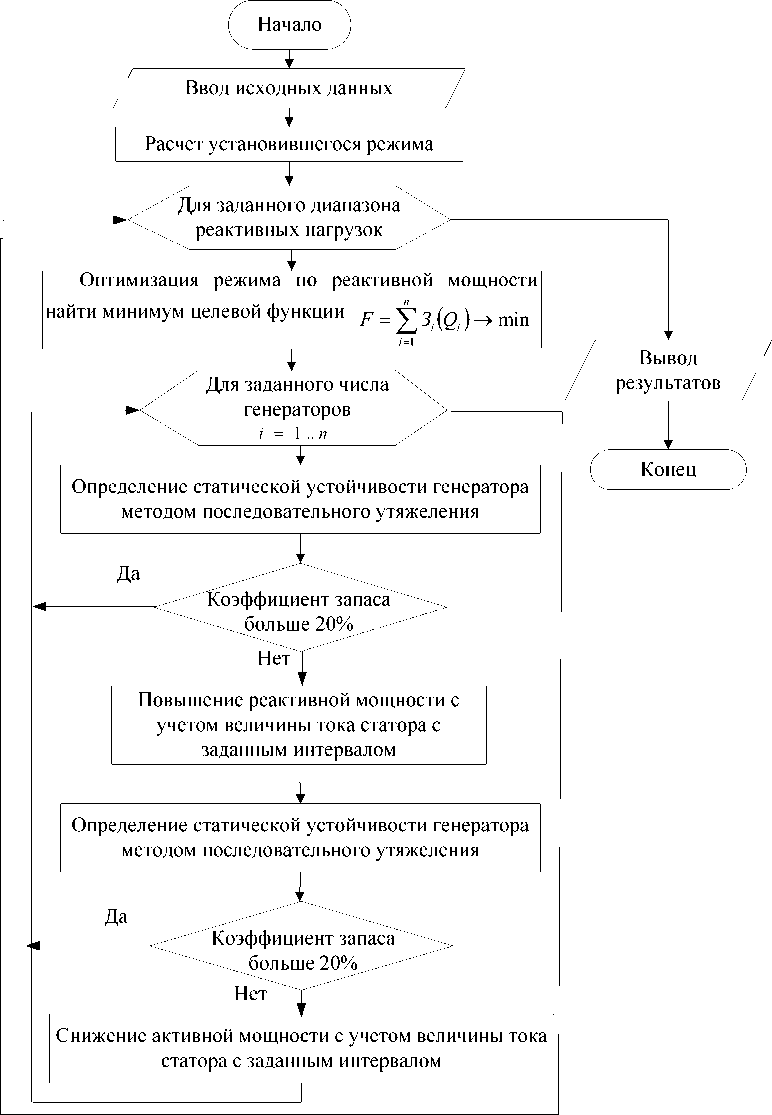
Рис. 1. Алгоритм, позволяющий определить оптимальный режим работы собственной электростанции по реактивной мощности

характеристики на прямом ходе и оптимальной загрузки каждого из генераторов на обратном ходе производится согласно алгоритму, приведенному в [1].

Оптимизация генераторов по реактивной мощности дает совокупность значений реактивных мощностей источников питания в сети. Однако особенностью ограничений (2) и (3) является их зависимость не только от паспортных характери- стик генераторов, но и от параметров режима. Следовательно, по результатам оптимизации должны быть произведены дополнительные исследования совокупности полученных выдаваемых реактивных мощностей в плане анализа статической устойчивости машин и оценки допустимости оптимального режима.

В связи с тем, что особенностью заводских систем электроснабжения являются частые рекон- струкции и изменения конфигурации, на среднесрочном горизонте планирования необходимо рассматривать несколько вариантов подключения потребителей реактивной мощности и величин их нагрузок. Для каждого выбранного варианта в сложнозамкнутой сети предполагается выявить оптимальный режим и исследовать статическую устойчивость генераторов с помощью метода последовательного утяжеления. При его применении в условиях параллельной работы с энергосистемой последовательно увеличиваются собственные углы роторов каждого из синхронных генераторов и определяется выдаваемая ими мощность. Максимальное значение мощности определяет предельную загрузку генератора по условию существования режима. В случае недостаточной величины коэффициента запаса необходимо повысить реактивную мощность с учетом допустимой величины тока статора и нагрузочной диаграммы машины. Если и при этом коэффициент запаса устойчивости не достаточен, предполагается снижение загрузки генератора по активной мощности с выбранным шагом. Разработанный программный комплекс «КАТРАН» позволяет произвести выбор оптимальных режимов и анализ статической устойчивости промышленных генераторов.

Результаты экспериментальных исследований

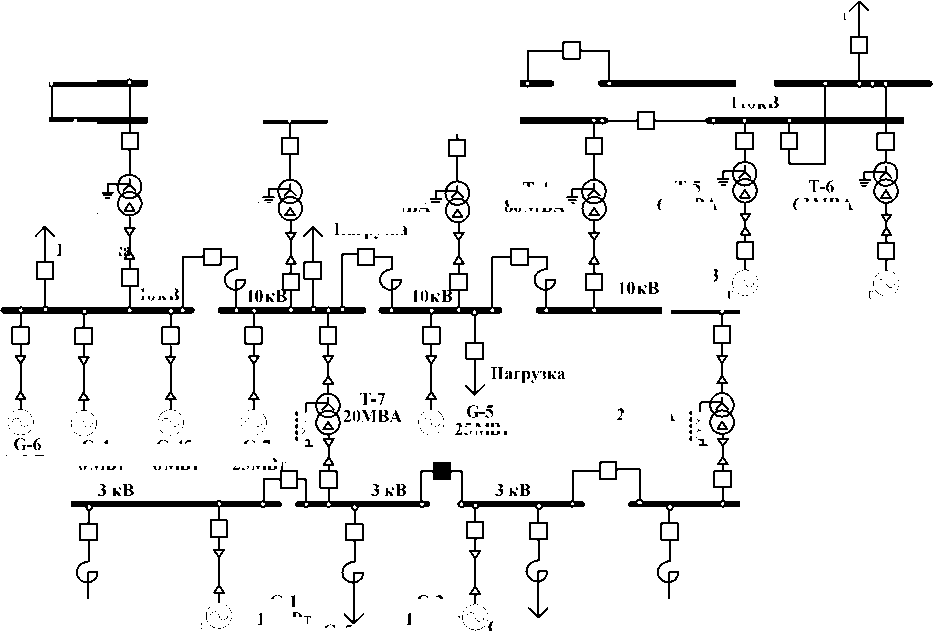
Исследования по предложенному алгоритму определения реактивных мощностей проводились на примере промышленного энергетического узла, в составе которого имеется три собственные электростанции суммарной установленной мощностью более 600 МВт. Схема исследуемого энергоузла приведена на рис. 2. Определение реактивной мощности с учетом потерь производилось для всех генераторов электростанций. В качестве примера выбрана электростанция ТЭЦ-1, схема электрических соединений которой приведена на рис. 3. Особенностью электростанции является значительная доля нагрузки на генераторном напряжении, а также разнородное оборудование с диапазоном установленных мощностей генераторов от 6 МВт до 50 МВт. Электростанция имеет две точки выдачи мощности (ПС 30 и ПС 60, рис. 2). Запас статической устойчивости генераторов исследуемой электростанции обусловлен мощностью короткого замыкания в точках связи с энергосистемой (связи с ПС «Бекетово», ПС «Шагол» и Ириклинской ГРЭС) и эквивалентными сопротивлениями связи между генераторами и энергосистемой.

Как видно из рис. 3, подключение новых потребителей возможно на напряжениях 3, 10 и 110 кВ. В качестве примера производилось увеличение реактивной нагрузки на шинах ТЭЦ-3, что равносильно повышению нагрузки ТЭЦ-1 на шинах 110 кВ. В ходе вычислительного эксперимента при неизменных заданных активных мощностях генераторов и нагрузок изменялись реактивные мощности узла с заданным интервалом. На основании разработанного алгоритма получены оптимальные загрузки генераторов по реактивной мощности рассматриваемого объекта.

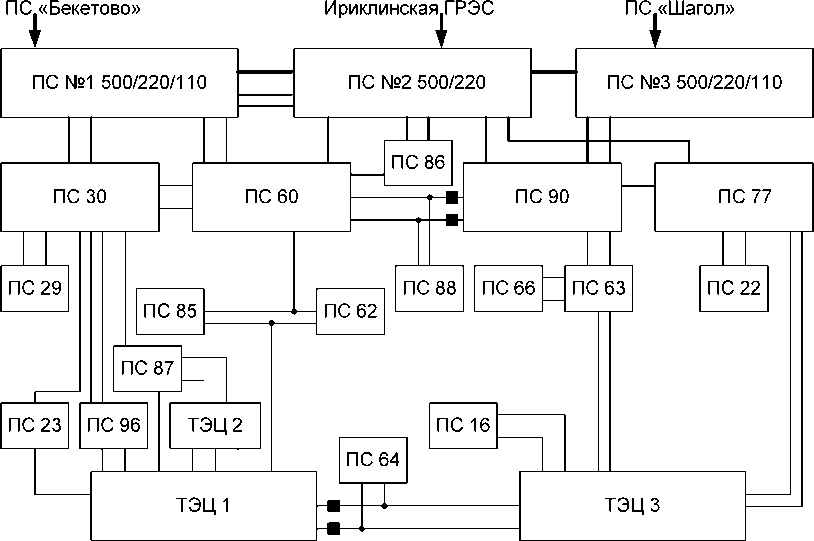
Рис. 2. Схема исследуемого энергоузла

Энергосистема

Энергосистема

Нагрузка

ПОкВ

ЮкВ

1 ЮкВ

25 МВт

63 МВА

Нагрузка

25 МВт

ЗкВ

•Собственные нужды

Собственные нужды

40 МВт

Собственные нужды

G-1

12 МВт

, 12МВт

Собственные нужды

Рис. 3. Исследуемая схема электрических соединений ТЭЦ-1

Т-1

40 МВА

Нагрузк

G-4a

6 МВт

Т-2

63 МВА"

G-46

6 МВт

G-7 25МВт

Т-3

63 МВА’ Нагрузка

Т-4

80 МВА’

Т-5 63 МВА

40MBi

Т-8

20МВА

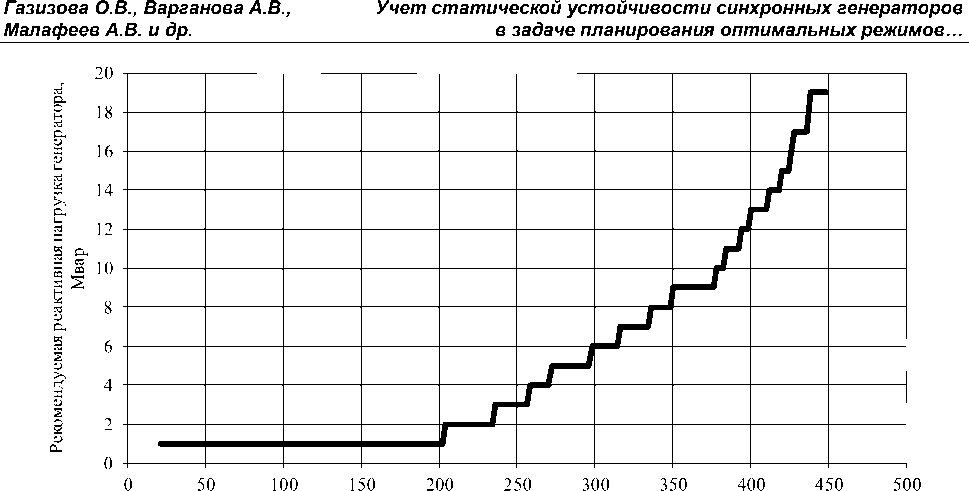
На рис. 4 и 5 показаны зависимости для наиболее экономичного (G-8) и для наименее экономичного генератора (G-6). По оси абсцисс показана суммарная реактивная нагрузка узла, показанного на рис. 2, по оси ординат – оптимальная выработка реактивной мощности соответствующего генератора. Как видно из рис. 4 и 5, выработка реактивной мощности генератором G-8 более экономична, поскольку его целесообразно загружать уже при наименьшем суммарном потреблении реактивной мощности узлом.

Поскольку нагрузка увеличивалась на шинах различного напряжения электростанции ТЭЦ-3, то есть вне района исследуемой ТЭЦ-1, то экономич-

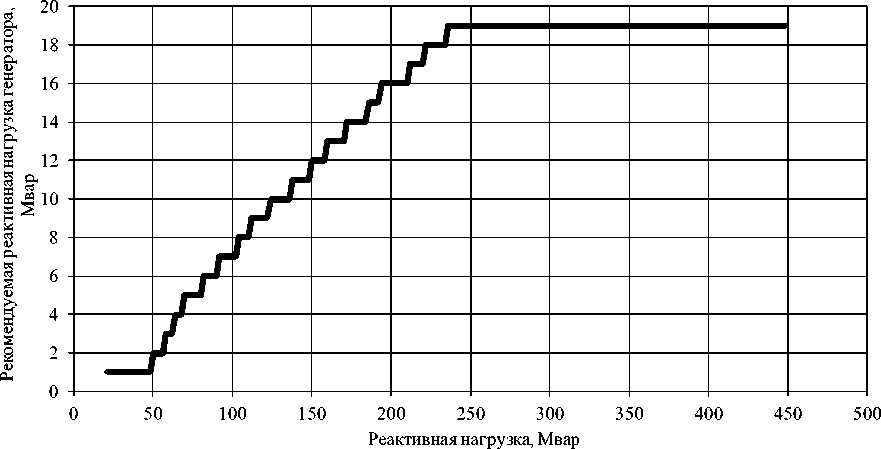
Рис. 4. Оптимальная загрузка генератора G-8

Реактивная нагрузка, Мвар

Рис. 5. Оптимальная загрузка генератора G-6

Влияние загрузки по активной мощности синхронного генератора на коэффициент запаса статической устойчивости

G-6, Рном = 25 МВт, Ртекущ = 27 МВт, Qтекущ = 8 Мвар, Qдоп = 16 Мвар G-8, Рном = 40 МВт, Ртекущ = 42 МВт, Qтекущ = 15 Мвар, Qдоп = 26 Мвар Qоптимальн, Мвар р „ предельн, МВт Коэффициент запаса, % Qоптимальн, Мвар р „ предельн, МВт Коэффициент запаса, % 4 45 67 4 72 71 8 47 74 8 73 74 12 48 78 12 74,5 78 16 50 85 16 76 81 20 51 89 20 77,5 85 нее грузить по мере роста реактивной нагрузки генератор G-8 как наиболее электрически близкий к энергосистеме, а затем генератор G-6. Полученные значения реактивных мощностей были проанализированы по запасу статической устойчивости. Для выбранных генераторов был определен коэффициент запаса статической устойчивости. Результаты расчета сведены в таблицу.

Как видно из полученных данных, достаточный запас статической устойчивости сохраняется. Однако при превышении 16 Мвар (для G-6) и 26 Мвар (для G-8) происходит перегрузка по току статора. Поэтому полученные рекомендованные реактивные мощности должны проверяться по ряду параметров, в том числе по коэффициенту запаса статической устойчивости, допустимому току обмотки статора и нагрузочной диаграмме синхронной машины. Решением является коррекция уставок регулятора возбуждения по предельным значениям реактивной мощности.

Заключение

Расширение промышленными предприятиями собственных источников генерации приводит к существенному усложнению вопросов управления нормальными режимами. В силу приближения нагрузок к генераторам повышается возможность питания потребителей реактивной мощностью непосредственно от шин последних. С целью повышения энергоэффективности функционирования системы электроснабжения встает вопрос оптимального распределения реактивных мощностей между собственными источниками питания.

На основе метода динамического программирования разработан алгоритм определения оптимальной загрузки генераторов по реактивной мощности по критерию минимума затрат на выработку и передачу реактивной мощности, положенный в основу одного из модулей программного комплекса расчета режимов «КАТРАН». Данный алгоритм апробирован на примере крупного энергетического узла, имеющего в своем составе три местные электростанции. При увеличении реактивной мощности нагрузки на шинах одной из электростанций получена оптимальная загрузка всех генераторов.

Разработанный алгоритм отличается от существующих возможностью учета при оптимизации режима статической устойчивости машин и распределения нагрузок в системе электроснабжения.

Для оценки статической устойчивости предложено использование метода последовательного утяжеления, позволяющего судить о сохранении устойчивости без непосредственного определения корней характеристического уравнения. Разработанные программный комплекс и алгоритм могут быть использованы для планирования нормальных режимов промышленных систем электроснабжения, имеющих источники распределенной генерации и существенные реактивные нагрузки на генераторном напряжении.