Учет влияния начального напряженного состояния скальных оснований гидротехнических сооружений на модели из гипсоизвестнякового композита

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 624.131.438                                    

Экспериментальные исследования напряженно-деформированного состояния скальных оснований гидротехнических сооружений в полевых условиях в большинстве случаев проводится на горных выработках – в штольнях, камерах и скважинах. Создание выработок, штолен, камер и скважин приводит к трансформации поле природных напряжений. При этом особенно возрастают составляющие напряжений на площадках, перпендикулярных направлению силового воздействия. Для оценки деформационных свойств гидротехнических скальных пород разработано [1, 4] несколько статических методов — штампа, гидравлических подушек, радиального пресса, скважинного дилатометра и т.д.

Крупномасштабные натурные исследования напряженно-деформированного состояния скальных оснований гидротехнических сооружений относятся к дорогостоящим процедурам. Полученные данные при помощи различных методов на одних и тех же массивах скальных пород дают существенный разброс. Кроме этого, не вполне определимо влияние на результаты испытаний природных напряжений. Поэтому считается целесообразным отдать предпочтение изучению лабораторных моделей, адекватных по физическим, прочностным и деформационным характеристикам скальных оснований [5, 6].

Экспериментальная задача моделирования скальных оснований гидротехнических сооружений с учетом начального напряженного состояния рассматривалась на модели из композитных материалов, в частности, гипсоизвестняковых материалов с целиком (Рисунок 1).

ВЕРТИКАЛИ

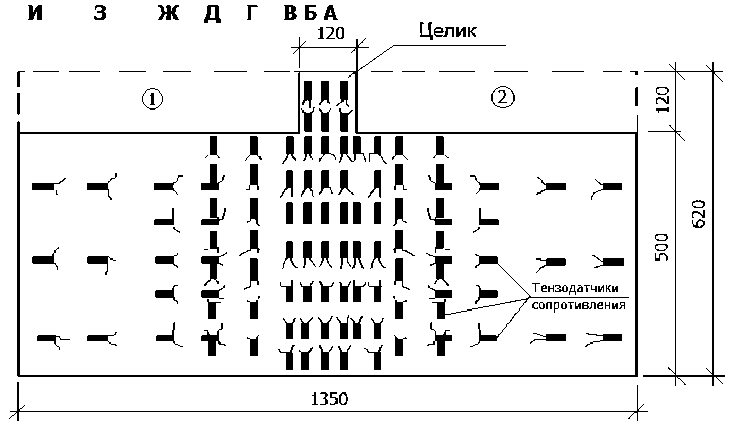
Рисунок 1. Модельное полотно из гипсоизвестнякового композита с наклеенными тензодатчиками сопротивления

При этом в материале реализовывалось плоское напряженное состояние. Опыты были поставлены в лаборатории скальных оснований Московского инженерно-строительного института им. В.В. Куйбышева. Из частей 1 и 2 материала модели изготовлены образцы для испытания на сжатие и растяжение. Эксперимента на сжатие осуществлялись на рычажном прессе с соотношением плеч 1:5 (Рисунок 2а) по стандартной методике на двенадцати образцах с размерами 0,04 х 0,04 х 0,14 м. А природных массивах скальных оснований при прохождении проходок (тоннелей) исследователи наблюдали такой эффект, так назывемыйц стреляние пород. Для проведения опытов на растяжение (Рисунок 2б) были подготовлены 6 образцов с размерами 0,04 х 0,06 х 0,24 м.

Результаты прозвучеивания образцов на приборе УКБ-1М было установлено, что динамический модуль упругости колеблется в пределах: Ед = (2300… 3200) МПа, для образцов на сжатие и Ед = (2838… 3836) МПа, для образцов на растяжение. Такой разброс значений динамических модулей упругости объясняется неоднородностью, обусловленный технологией изготовления модельного полотна.

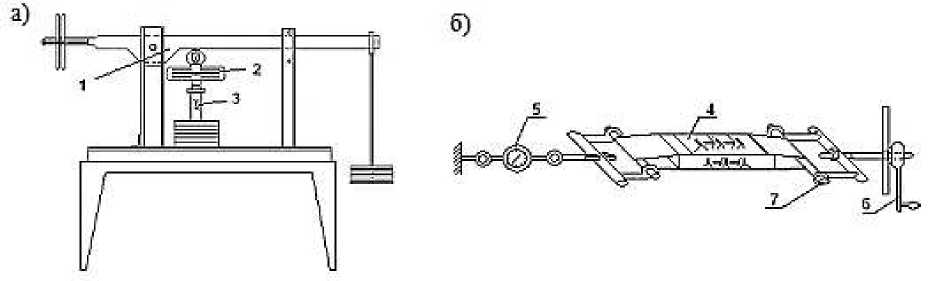
Рисунок 2. Испытание образцов из гипсоизвестняковых композитов на рычажном прессе (а) и приборе для испытания образцов на растяжение (б). 1 – рычажной пресс; 2 – динамометр ДС-0,5; 3 – образец на сжатие; 4 – образец на растяжение; 5 – динамометра ДР-0,5; 6 – рукоятка для придачи растягивающей нагрузки; 7 – приспособление для захвата образца

Соотношение пределов прочности на растяжение и сжатие у разных скальных пород имеет разное значение и надо предположить, что деформационные характеристики на сжатие и растяжение также отличаются между собой. К сожалению, этот параметр учеными исследователями не изучался. Только некоторые исследователи, такие как Осидзе В. И., Сахновского К. В., Цискарелли Г. Д. [7], Симонова М. З. [8] и Амбарцумян С. А. [9] при исследовании бетона констатируют необходимость учета разных модулей при растяжении и сжатии строительных конструкций. Результаты испытания образцов на сжатие и растяжение приведены в Таблице.

Таблица

Наименование	Ед. изм.	Величина	Примечание
Предельная  призменная  прочность  модельного	МПа	3,22÷5,3	Образцы
пр . полотна R сж Статический модуль общей деформации Е 0 сж .	МПа	2300÷3200	размером (4х4х14) · 10-2 м, испыт. на
Коэффициент поперечной деформации μ сж	-	0,188÷0,290	сжатие
Предельная  призменная  прочность  модельного	МПа	0,45÷0,61	Образцы
пр . полотна R рас .			размером (4х6х24) · 10-2 м,
Статический модуль общей деформации Е 0 рас .	МПа	2838÷3836	испыт. на
Коэффициент поперечной деформации μ рас.	-	0,187÷0,403	растяжение

Первоначально на выделение целика из полотна модельного материала возлагалась надежда на возможность определения деформационных и прочностных характеристик путем испытаний его на сжатие, отрыв и сдвиг. Такой подход мог бы дать преимущества сравнительно с опытами на жестких штампах. Обеспечение жесткости целика проверялось по показателю гибкости М. И. Горбунова-Посадова [1] в виде:

12 π а ² вЕ (1 - µ ² )

Н ² Е 1 (1 - µ 0 ² )

здесь 2а, 2в — соответственно меньшая и большая стороны целика; h — высота целика; Е1 = Е0 и μ1 = μ0 — соответственно модуль упругости и коэффициент поперечной деформации целика и модели из гипсоизвястникового композита. Формула (1) позволяет установить ограничение на высоту целика. Поскольку имеет место неравенство 0 < Г < 8/ 4а , где α=а/в, то для рассматриваемого случая α=0,75, при котором жесткость целика считается конечной. Полагая для Г предельный случай, т.е. Г = 8/ 4а , будем иметь Г=9,24. Решая зависимость (1) относительно h, получаем наименьшую высоту «целика-штампа» из условия обеспечения жесткости целика по отношению к испытываемому модельному основанию, равную:

• ₂                1 ₃

Н = ----—  - 10,552 - 10 ^{- 2} м

к         2

Полученный результат позволяет утверждать, что условие жесткости ( H = 12·10^-2 м > 10,552·10^-2 м) целика выполняется. Будем считать, следуя [1, 4], что материал модели по своим механическим характеристикам соответствует реальному массиву скальных пород. На Рисунке 3а схематично изображен рычажной стенд с моделью из гипсоизвестнякового композита с целиком. Эксперимент состоял из отдельных опытов с различными значениями равномерного давления, прикладываемого по горизонтали к боковым граням плоской модели (σ x ) и вертикали на «штамп-целик» (σ z ). При нагружении соблюдались условия, в соответствие которому составляющие напряжений σ x и σ z не должны превышать 70% призменной прочности, установленной при испытаниях образцов на сжатие и растяжение (Таблица).

Горизонтальные давления (Рисунок 3) создавались при помощи шести домкратов (по три домкрата с каждой стороны) и выдерживались постоянными при значениях: 0; 0,05; 0,10; 0,15 МПа. Затем производилась разгрузка модели в обратном режиме. Результаты опытов показали, что после разгрузки модель полностью восстанавливала размеры и форму, то есть остаточные деформации не возникали.

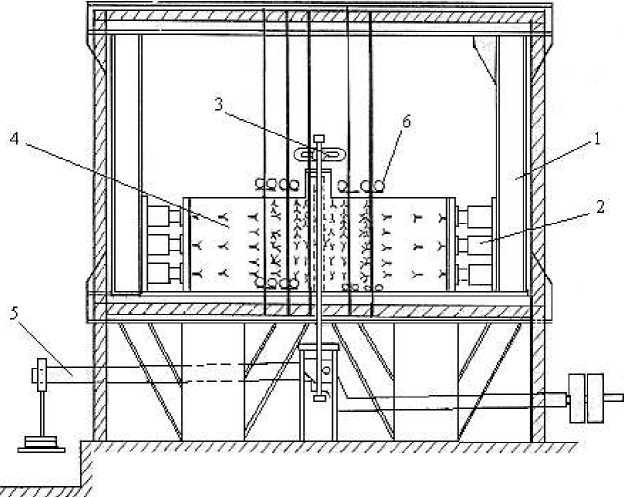
Рисунок 3. Схема испытания гипсоизвестняковой модели с целиком: 1 – стенд для испытания плоских моделей; 2 – гидравлические домкраты; 3 – динамометр пятитонный; 4 - плоская модель с целиком; 5 – рычажная силовая установка с соотношением плеч 1:10, для вертикальной нагрузки модели; 6 – мессуры, индикаторы часового типа (тысячники)

В дальнейших опытах при постоянном горизонтальном давлении на модель прикладывались вертикальная нагрузка тремя ступенями на целик через жесткий штамп с последующей разгрузкой. Такое ступенчатое изменение потребовалось для набора данных, необходимых для статистической обработки. При этом величина вертикального давления доводился до максимума 0,3 МПа, а за тем производилась полная разгрузка. После снятия нагрузки модель выдерживалась не менее двух часов для ликвидации упругого последствия. Тот же опыт повторялся для всех значений горизонтальных давлений. Для измерения деформаций модельного поля использовались проволочные тензодатчики сопротивления, методика применения которых апробировалось автором [2]. Относительные деформации определялись с помощью комплекта цифровой тензометрической аппаратуры ЦТК-1 с точностью 1·10-5. Тензодатчики в количестве 194-х штук, наклеены на поверхности модели из нипсоизвестнякового композита согласно схеме симметрично относительно центральной оси. Поэтому значения деформаций определялись как среднее результатов по двум датчикам по вертикали А (Рисунок 2 б), а для остальных — по четырем датчикам. Показания датчиков фиксировались после приложения нагрузки. Следующий замер производился после 30минутной выдержки с целью выяснения изменения деформаций во времени. Оказалось, что фактор времени не имеет существенного значения. Как указывалось выше, между сериями опытов модельное полотно оставалось ненагруженным в течение двух часов.

Анализы результатов эксперимента представлены на Рисунке 4а в виде эпюр изменения относительной продольной деформации ε z от глубины. Величина вертикального давления сохраняется, как уже отмечалось, постоянной и равной 0,3 МПа, а горизонтальное давление изменяется ступенями.

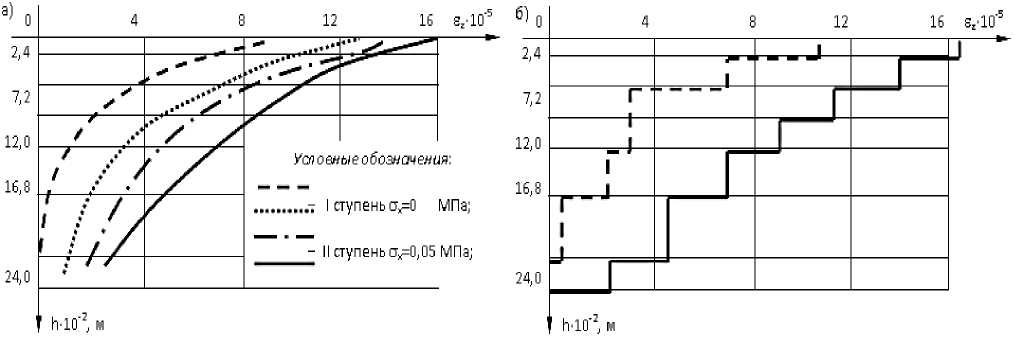
Рисунок 4. График изменения относительных деформаций в вертикали «Б» с глубиной при Ϭ_z = 0,3 МПа и Ϭ x = 0,00 ÷ 0,15 МПа. а) полученные результаты опытов; б) приведенный график для определения осадки

Результаты опытов показывает, что:

• -    наибольшие относительные продольные деформации ε z имеет место в точках модельного поля, расположенных в целике и вблизи него;

• -    с увеличением горизонтальных давлений деформации  ε z на всех уровнях

уменьшаются.

Абсолютную осадку какой-либо точки модельного поля можно определить как площадь эпюры εz — h. Напомним, что значение деформаций фиксировались в определенных точках модельного поля, причем горизонтальные давления прилагались ступенями. Криволинейные эпюры εz – h для первого и четвертого этапов горизонтального загружения заменим ступенчатым графиком обеспечением равенства этих площадей. Величину абсолютной осадки S подошвы «целика-штампа» с использованием ступенчатой эпюры εz – h определим по формуле:

S = hε

i zi где: hi — толщина выделенного элемента, в пределах которого относительная деформация считается постоянной, εzi — относительная деформация отдельных элементов под «целиком-штампом». При известной величине осадки модуль общей упругости легко вычисляется. Имеем

K

Е о „ ,

S о

Здесь для К получено /4/ K = апл(1 — Д2)вР причем ипл — коэффициент, зависящий от , местоположения точки, Р — величина давления под «целиком-штампом» (Р = 0,3 МПа), в — ширина целика.

Расчеты по результатам опытов показали, что значения модуля общей деформации Е 0 =8083,3 МПа превышает значение Е 0 =2923,22 МПа, установленное при отсутствии бокового давления. Последнее значение Е 0 соизмеримо с полученными на образцах. Следовательно, влияние схемы напряженного состояния на механические параметры оказываются ощутимым,следует учитывать при проектировании и строительстве гидротехнических сооружений.