Учимся у Галилея

Имя Галилея(1564-1642)хорошо известно каждому школьнику. С ним связывается прежде всего коперниканская революция.

И действительно он был первым (или одним из первых), кто не только создал новый увеличительный прибор - телескоп, но и догадался направить его на небесные тела. Он увидел спутники Юпитера - прообраз Солнечной системы и фазы Венеры как доказательство ее вращения вокруг Солнца, солнечные пятна и горы на Луне, что разрушило аристотелевское представление об идеальности небесных тел в отличие от несовершенства земного мира. Ему открылись новые, нивидимые простым глазом звезды, а Млечный Путь предстал просто скоплением огромного количества звезд.

Все это изменило картину мира не только для ученых, но и для всего человечества, хотя убедить в своей правоте других оказалось непростой задачей, потребовавшей от Галилея особой литературной работы, необычайной силы убеждения. Его «Диалоги о двух системах мира», «Беседы и математические доказательства» и «Пробирщик» были отражением

* Статья подготовлена в рамках проекта Российского гуманитарного научного фонда № 13-03-00190 «От технонауки Галилея до нанотехнонауки (философско-методологический анализ)».

ГЛАВНОЕ - КАЧЕСТВО

тех реальных споров и дискуссий, которые разгорелись тогда вокруг его «Новой науки». Но именно эта литературная деятельность, разворачивание аргументации и системы доказательств заложили основы для становления новой научной литературы.

Произошел социокультурный сдвиг - научная картина мира заменила мифологическую. Все это так. Но из этого, казалось бы, простого и очевидного для нас факта, который не был таким очевидным для современников Галилея, вытекают два важных следствия, изменившие ход и направление самого научного поиска и научное мировоззрение.

Во-первых, небесные явления надлунного мира перестали быть прибежищем идеальных движений и тел, а предстали вооруженному телескопом глазу такими же несовершенными, как и окружающие нас земные объекты. Особенно рельефно это выразило открытие Галилеем гор на Луне, переставшей быть гладким идеальным шариком и ставшей внезапно подобной нашей несовершенной Земле. Следствием этого явилась возможность применения математических знаний и представлений для описания не только небесных, но и прежде всего земных явлений. До этого считалось, что идеальные геометрические сущности реализуются только на небе, а астрономия причислялась к математическим, а не физическим наукам.

Во-вторых, применение телескопа открыло новый способ исследования природных явлений с помощью экспериментального оборудования и технически подготовленного эксперимента, ставшего важнейшим аргументом научного доказательства.

Но почему Галилей вообще стал использовать технические средства для изучения природы? И почему обратился именно к геометрии для описания земных при родных явлений? Начнем с последнего из этих вопросов.

С точки зрения античной и средневековой науки Евклидова геометрия реализуется в надлунном мире. Именно там существуют в реальности идеальные геометрические тела - круги, шары и равномерное круговое движение. По Аристотелю, такое движение, являясь движением, в то же самое время оставляет небесные тела на одном и том же месте. Сами же небесные тела - планеты (в том числе и Луна) - представляют собой идеально гладкие шары. Тогда становится понятна революционность утверждения Галилея, показанного им наглядно с помощью телескопа, что Луна имеет шероховатую поверхность, горы и впадины. Почти никто в это не поверил. Например, один из приверженцев аристотелевских взглядов утверждал, что «лун ные горы и долины покрыты прозрачным веществом, похожим на лед; таким образом луна сохраняла идеальную сферическую форму» [4, с. 121]. Мы действительно часто видим реальный мир через призму теории, а тогдашние ученые видели его через призму аристотелевской теории устройства мироздания, ставшей официальной доктриной католической церкви. Од-

ВИТАЛИЙ

ГЕОРГИЕВИЧ

ГОРОХОВ доктор философских наук, профессор, специалист в области философии и методологии науки и техники, главный научный сотрудник сектора междисциплинарных проблем научно-технического развития, руководитель Центра фило

софии техники и инженерной этики Института философии Российской академии наук, заведующий кафедрой философии науки и техники Государственного академического университета гуманитарных наук, руководитель российско-германской магистерской программы «Философия и европейская культура» философского факультета Московского государственного университета им. М.В. Ломоносова, ученый секретарь и действительный член Международной академии устойчивого развития при университете г. Карлсруэ (Германия). Сфера научных интересов: философия науки, техники и окружающей среды, глобальные проблемы устойчивого развития, оценка последствий научнотехнического развития, методология системотехники и проектного менеджмента, история инженерии и методологический анализ технического знания. Автор более 300 публикаций

Галилео Галилей

нако, кроме мировоззренческих последствий, это открытие имело важнейшее методологическое следствие.

Если небесные тела так же несовершенны, как земные, а к ним применима Евклидова геометрия, то значит она может быть использована и для описания земных явлений. Вот вам исходная установка метаматизированного естествознания, выраженная в словах Галилея, что книга природы написана на языке математики. Такой переход научного сообщества к метаматизированному мышлению был подкреплен инженерной практикой создания и использования начиная с эпохи Возрожде-

Артиллерийская угольник для измерения поднимающихся дуг

Стереометричекие линии для измерения объемов

гапсадля измерения поднимающихся дуг

Рис. 2. Изобретенный Галилеем «математический компас» как измерительный инструмент и пособие для обучения военно-инженерному искусству

Рис. 3. Изображение процедуры измерения высоты с помощью «математического компаса»

ния так называемых математических инструментов в артиллерии и фортификации.

С развитием тяжелой артиллерии и огнестрельного оружия мир кардинально изменился. Старые крепостные стены больше не защищали, а от дальности стрельбы из пушек и точности попадания в цель зависело выживание тогдашних городов-государств. Технический прогресс в военной сфере становится с этого времени определяющим. Во время Первой мировой войны, например, немец

Металлические линии для определния удельного веса золота, свинца, серебра, меди, железа и олова

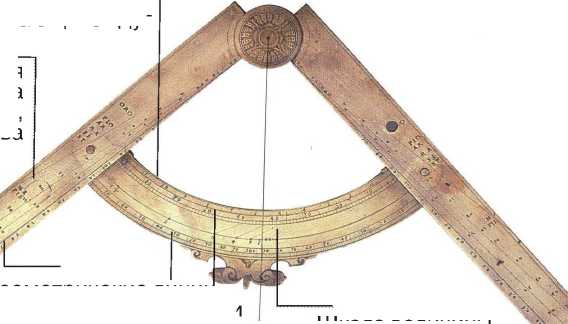
метические линии для *-метических операций и линейных измерений |_____

Шкала величины уклона для измерения' наклонной плоскости *

свинцовый груз

Геометричекие линий ~ для измерения площади поверхностей

Астрономичесикй угольник для измерения склонения небесных тел

Теневой угольник для измерения дистанций кие корабли становились беззащитной мишенью более мощных английских пушек и могли только спасаться бегством, надеясь на свои более мощные паровые двигатели. Классический пример -бегство крейсера «Дрезден», на котором служил старшим лейтенантом будущий адмирал Канарис, от английского флота во время Первой мировой войны у берегов Южной Америки [8]. Аналогичная ситуация сложилась и в Италии. Например, Республика Венеция была всерьез озабо чена постройкой нового большегрузного (чтобы нести тяжелую артиллерию) и одновременно маневренного флота, чтобы противостоять флоту Османской империи. Наряду с относительно простыми средствами (например, укрепление крепостных стен снаружи ящиками с землей, в которых увязали ядра) стали необходимы точные расчеты траектории полета снарядов и сложные геометрические расчеты дальности с помощью новых «математических» инструментов. От точности попадания в цель и дальности полета снарядов в буквальном смысле зависило выживание ренессансных городов-государств. Поэтому на первый план в качестве инженерной элиты наряду с мастерами-инженерами, вышедшими из среды ремесленников, становятся военные инженеры, получавшие специальное математическое образование.

Производство именно «математических» инструментов, потребность в которых возникла в ту эпоху, и организовал Галилео Галилей. Особенностью его предприятия было, впрочем, не только производство и продажа «математического компаса» или циркуля (рис. 2), но и трансляция знаний по его использованию с обучением основам практической математики [11, р. 44]. Поэтому можно считать, что Галилей является основоположником научного образования инженеров, а его военный компас для различных точных измерений в артиллерии и фортификации служил также учебным пособием для обучения практической математике [6, р. 32] (рис. 3).

Эти инженеры проходили специальный курс обучения не только на предприятии в ходе работы, но и в появившихся тогда академиях. Например, основанная в 1562 году Флорентийская академия искусств (Accademia del Disegno), которую на русском языке обычно называют Академией изящных искусств или рисунка, была, скорее, Академией дизайна или, лучше сказать, искусства проектирования, поэтому ее часто называли «академией делания», а также учебным заведением для подготовки мастеров-инженеров. Ее студенты изучали геометрию и черчение, в том числе техническое черчение. Учитель математики Галилея Остилио Риччи (15401603) получил в ней в 1593 году кафедру математики. Одновременно он давал уроки практической геометрии в мастерской Бернардо Буонталенти (1536-1698). Эта академия стала образцовой моделью обучения художников, инженеров, практических математиков. Галилей, наряду с учебой в Падуанском университете, прошел все стадии тогдашнего инженерного образования, а позже и сам организовал обучение военных инженеров.

Однако это не было чисто коммерческой деятельностью, изолированной от его научных интересов. Создаваемые им «математические инструменты» могли применяться только вместе со знаниями о том, как их использовать. Поэтому кодификация и передача таких знаний с помощью частных уроков были главной деятельностью Галилеева предприятия (рис. 3). В это время становится нормой для успешной военной карьеры брать частные уроки по фортификации, военной архитектуре, геодезии, механике, теории перспективы и пользованию военным компасом. Одной из главных особенностей уроков, даваемых Галилеем, было длительное и детальное объяснение того, как правильно использовать «математические инструменты» (измерительные приборы). Но Галилей идет дальше и создает новую эпистемологическую модель генерирования естественнонаучных знаний.

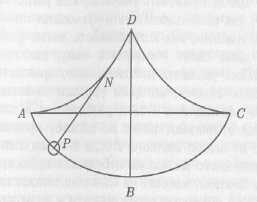
Одним из наиболее характерных примеров является маятник. Еще до развития Галилеем физи ческой теории качания маятника его применяют в некоторых машинах, например в механической приводной пиле с тяжелым якорным маятником, как его описывает французский инженер Жак Бессон в своем труде «Театр инструментов и машин» [9, р. 21] (рис. 4).

Однако у Галилея маятник - это не просто инструмент для приведения в движение машинного механизма, а идеализированный объект естественнонаучной теории - математический маятник, с помощью которого он открыл закон колебания маятника: независимость периода колебания при малых амплитудах (изохронизм). Именно с его помощью Галилей сравнивает качание пробкового и свинцового шара - «свинцового маятника» в мысленном эксперименте. В своем трактате «Беседы и математические доказательства» Галилей использует математический маятник для объяснения самых различных физических явлений, связанных с движением: даже если оба шара - свинцовый и пробковый - «начнут свой путь в одно и то же время, однако пробковый, будучи отклонен в сторону на тридцать градусов, должен будет проходить дугу в шестьдесят градусов, а свинцовый, отведенный только на два градуса,— дугу в четыре градуса? Не окажется ли в таком случае скорость пробки большею? А опыт показывает, что таки произойдет» [1, с. 181-182]. Таким образом, в естественнонаучной теории строятся различные теоретические схемы, позволяющие делать теоретические выводы о природных процессах, которые могут быть проверены в технически подготовленном эксперименте (рис. 5). «Я верю, что железный шар, покрытый свинцом, на батарее города Корбель не наносил особого урона неприятелю и что железное ядро оказалось испорченным свинцом. Я не верю другой части... относящейся к физике, - о том, что свинец плавится

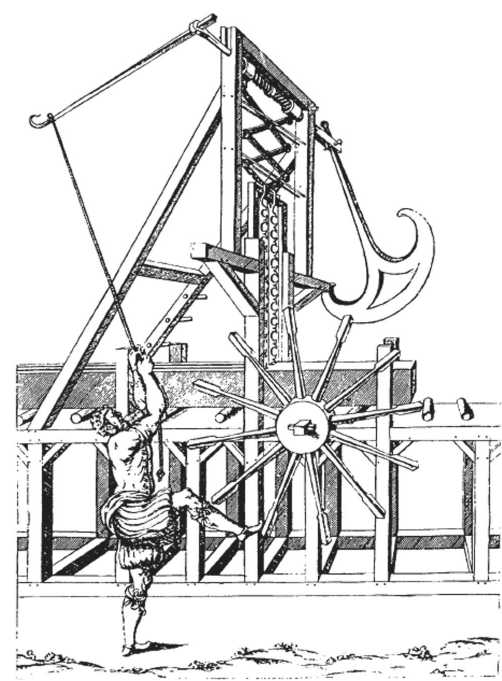
Рис. 4. Пильный станок с тяжелым якорным маятником и вследствие этого железный шар утрачивает в полете свою свинцовую оболочку» [3, с. 214]. Далее, Галилей ссылается на опыт, приводимый Аристотелем, что на пущенной стреле с воском не плавится даже воск. Галилей задал методологию теоретического конструирования - проектирования различных экспериментальных ситуаций для получения новых знаний о природе - мысленного эксперимента.

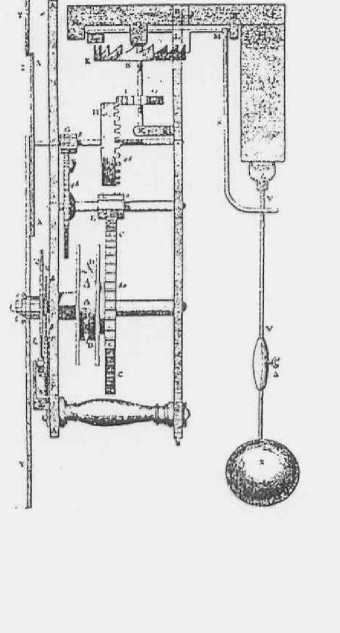
Эту методологию успешно использовали его последователи. Замещая техническую задачу физической проблемой, а затем математическим представлением, голландский ученый Христиан Гюйгенс переходит к решению математической задачи: по какой кривой должна двигаться точка, чтобы период ее колебаний не зависел от амплитуды, т.е. - в терминах физической проблемы, эквивалентной этой задаче, - чтобы время качания маятника не зависело от величины его размаха. Используя учение Галилея о свободном падении тел и геометрические представления, он конструирует новое экспериментальное оборудование - маятниковые часы с изохронным качанием [7, s. 3-4] (рис. 6). Такой способ сое-

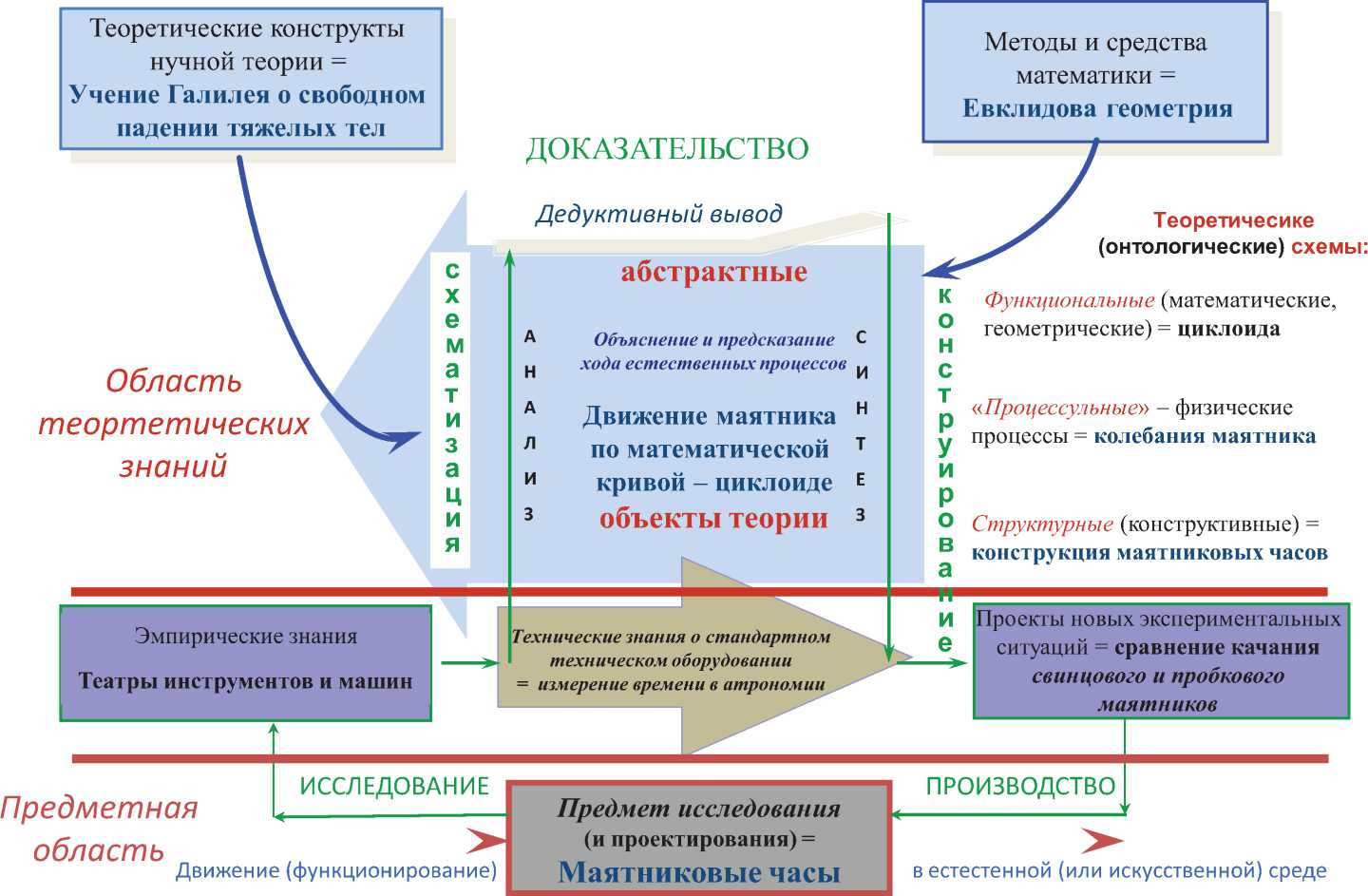
Рис. 5. Структура и функционирование естественнонаучной теории

динения науки и техники становится характерным как для экспериментального математизированного естествознания, так и для основанной на науке техники.

В отличие от схоластической точки зрения, согласно которой законы природы и законы механики принадлежат различным реальностям, и мнения многих тогдашних инженеров-практиков, что механические искусства выше природы и помогают человеку господствовать над ней, Галилей считал, что законы природы и законы механики принадлежат одной и той же области. С этой позиции он критиковал инженеров-практиков, стремящихся строить машины, противоречащие законам природы. «Новая наука» Галилео Галилея пытается разработать научные средства для решения практических инженерных проблем. И хотя сам Галилей не занимался постройкой и конструированием машин, он принадлежал к тем экс пертам, которые контролировали качество и осуществляли оценку машин и их проектов. Главным в такой оценке было определить, является ли представленная модель той или иной машины действительно выполнимой при переходе к реальной конструкции.

Эту проблему - разработать научные средства для решения практических инженерных проблем -пытался решать еще Леонардо да Винчи [12], который конструировал всякого рода колесные механизмы, аналогичные принципу своего действия часовым механизмам. Сам Леонардо соорудил несколько таких автоматов. Чтобы их построить, он тщательно изучал природные объекты: строение человеческого организма и механизм движения животных, рассматривая живой организм как умную машину [13, р.174]. Одним из наиболее интересных достижений Леонардо да Винчи было создание проектов автоматических саморегулиру ющихся устройств, создаваемых на основе сходства с деятельностью человека или животного. «Автоматы Леонардо были результатом исследования, осуществлявшегося мастерами-инженерами в области анатомии и кинетической физики... фактически, изучая человеческое тело, он приходит к созданию прекрасных человекоподобных машин». Одним из примеров такой машины была ра-работанная им модель автомата-барабанщика [12, р. 44, 66]. Леонардо, чтобы построить модель такого автомата, тщательно изучал сам этот инструмент и игру (деятельность) барабанщика на нем.

В эпоху Ренессанса согласие между божественным планом и новыми математическими истинами достигалось пониманием Господа как Инженера, действующего в своем космологическом проектировании в соответствии с им же установленными математическими закона-

Оригинальный чертеж

Конструкция часов

часового механизма, сделанный Гюйгенсом

Точка возврата

Циклоида

Направляющая прямая

Вершина

радиус

Точка возврата

В основание = 2ла

Общий вид циклоиды и изображение одной арки

с производящим кругом

Рис. 6. Описание часового механизма у X. Гюйгенса: математическое (математическая кривая - циклоида), физическое (качание гравитационного маятника) и конструктивное (конструкция часового механизма - специально изогнутые направляющие для получения движения по циклоиде)

ми. Исследуя эти продукты божественной технической деятельности в природе, мастера-инженеры стремились воссоздать математические принципы их построения в искусственных сооружениях. При этом каждое такое открытие или изобретение рассматривалось как продукт божественной инженерной работы. Именно эти мастера-инженеры провозглашали необходимость особой новой «scienza activa» (деятельностной науки), т.е. фактически технонауки, изучающей функции строения человеческого организма и структуры машины как основы технической практики [13, р. 167, 168, 174, 182].

«Новая наука» Галилея, в частности, давала возможность помочь мастерам-разработчикам и строителям различного рода ма шин решать эти проблемы, получать ответы об их надежности и работоспособности еще до постройки и испытания самой машины. Поэтому он начинает свой трактат по механике следующим призывом, в котором сформулирована его программа теоретического анализа механических орудий: «...Чрезвычайно важно рассмотреть их в общем и уяснить себе, каковы те выгоды, которые получают от этих орудий...», поскольку «...механики часто заблуждаются, желая применить машины ко многим действиям, невозможным по самой своей природе, а в результате и сами оказываются обманутыми и в равной степени обманывают тех, кто исходил в своих надеждах из их обещаний» [1, с. 7]. Именно поэтому мы можем квалифицировать «но вую науку» Галилея одновременно как зачаток технической науки. Геометро-кинематическая схема Галилео Галилея, модифицированная Гаспаром Монжем в проективную геометрию, послужила началом приложения естественнонаучной теории - теоретической механики к описанию машин и толчком для создания технической науки - теории механизмов и машин (рис. 7). К концу XVIII - началу XIX столетий появляется такое огромное количество сложных машин (в том числе астрономических, математических и физических аппаратов и инструментов) [10], требующих к тому же точных расчетов, что Евклидовой геометрии уже недостаточно было для их графического представления. Уже в середине XVIII столетия в опубликованном немецким

Базовая естественнонаучная теория:

Геометрические методы расчета механизмов

Методы и средства математики:

начертательная геометрия Гаспара Монжа

Область

теоретических знаний

геометро-кинематическая схема Галилея;

теоретическая кинматика

с X е

▲ м

Да

И

А л и

А

Н

а Ц и

Кинематический анализ я

Конструктивно-технические и технологические знания частей и типов машин

Область функционирования инженерной деятельности

синтез

ДОКАЗАТЕЛЬСТВО кинематический

Дедуктивный вывод

абстрактные теоретические объекты

Кинематические пары, звенья, цепи и механизмы

Тиражирование структурных схем машин

Эмпирический базис технической теории

с

И

Н

т

Е

к о с т р У и р о в а н w е

ртеические(онтологические) -схемы:

Функциональные (математические) - геометрическое представление машины

«Процессуальные» - кинематическая схема механизма

(геометрическая модель движения)

Структурные (конструктивные =

«конструктивный» механизм

Якоб Лейпольд «Театр машин»

Практико-методические знания -общая классификация механизмов и их частей

ИССЛЕДОВАНИЕ

Техническая система =

ПРОИЗВОДСТВО

эксплуатация

МАШИНА

(предмет исследования и проектирования)

^- Новые типы функционирование мехЗНИХМОВ

Рис. 7. Структура и функционирование технической теории в теории машин и механизмов механиком Якобом Леопольдом (1674-1727) с 1724 по 1739 год трактате «Театр машин» (Teatrum machinarum) для эмпирического описания существовавших к тому времени машин с попыткой их систематизации потребовалось 10 томов. Важный шаг от чистой математики в сторону ее приложения к описанию конкретных машин сделал в своей начертательной геометрии Гаспар Монж.

Начертательная геометрия давала инженерам математически точную систему графических изображений (математическую схему), позволяющую схематизировать пространственные структуры в виде плоскостного изображения, проводить на нем необходимые расчеты с помощью стандартизованных математических преобразований, а затем переносить полученные результаты в реальные условия. Чертежи и схемы для инженера становятся од новременно и средством связи, с одной стороны, с наукой, а с другой - с реальным миром технической практики. Однако потребовалась и другая наука - техническая наука, которая в отличие от естествознания призвана была выработать теоретические средства для анализа и синтеза машин во всей их сложности, используя одновременно последние достижения естествознания и математики.

Эта задача была связана с использованием теоретических средств анализа и синтеза сложных машин из стандартных компонентов. Значительный вклад в их создание внес немецкий инженер Франц Рело, который построил особую «кинематическую геометрию» и с ее помощью провел детальное расчленение машины на части в виде иерархического описания механизма, состоящего из кинематических пар, звеньев и цепей. В своей книге «Тео ретическая кинематика», опубликованной в 1975 году, Рело дал следующее определение машины совсем в духе Галилея: «Машина — это соединение сопротивляющихся тел, устроенное так, чтобы принудить механические силы природы действовать для выполнения определенных движений» [15, s. 38]. Поскольку же все механизмы оказываются собранными из одного и того же набора типовых элементов, то остается задать лишь определенные процедуры их сборки и разборки из идеальных цепей, звеньев и пар элементов, т.е. синтеза и анализа (рис. 7). Машины, по Рело, «представляют собой особый вид, активируемый с помощью вращающихся везде геометрических структур», которые есть не что иное, как «душа машины», «геометрическая абстракция машины» [4, s. 59, 60, 87, 88]. Здесь опять налицо продолжение Галилеевой модели на- уки о машинах, основанной на математике. Для анализа машин Галилей обязательно переходит к их геометрическому представлению для объяснения принципа работы машины [6, р. 101] (рис. 8).

Мы видим, что «новая наука» Галилея может по-праву называться технонаукой, хотя этот термин сегодня относится к нано- и биотехнологиям. Но именно Галилеева наука содержала в себе ее зародыш, от которого отпочковались как естественные, так и впоследствии технические науки.

Обычно отмечают, что Галилей полностью отверг аристотелевскую физику и основывает свою «новую науку» на эксперименте и технических знаниях. Отчасти это, конечно, верно. Но и Галилей, и инженеры того времени с большим пиитетом относились к античной науке. Важно учитывать социокультурную обстановку раннего Нового времени в Италии.

В книге Матео Валериани «Галилео - инженер» [6] приводится интересный пример с выбором на конкурсной основе проекта нового корабля - знаменитой вени-цианской галеры. По традиции к рассмотрению комиссии Вени-цианского сената были приняты три проекта, два из которых были представлены известными кораблестроителями - практическими инженерами, а третий - ученым-гуманистом В. Фаусто (14801546), переводчиком с древнегреческого на латинский труда «Механические проблемы», приписываемого тогда Аристотелю, а сегодня обозначаемого как труд псевдо-Аристотеля. Последнее обстоятельство не имеет в данном случае большого значения, так как в то время верили, что это продукт творчества самого Аристотеля. Интересно, что конкурс выиграл Фаусто, не имевший никакого практического опыта в строительстве кораблей, и именно потому, что он утверждал, что грече-

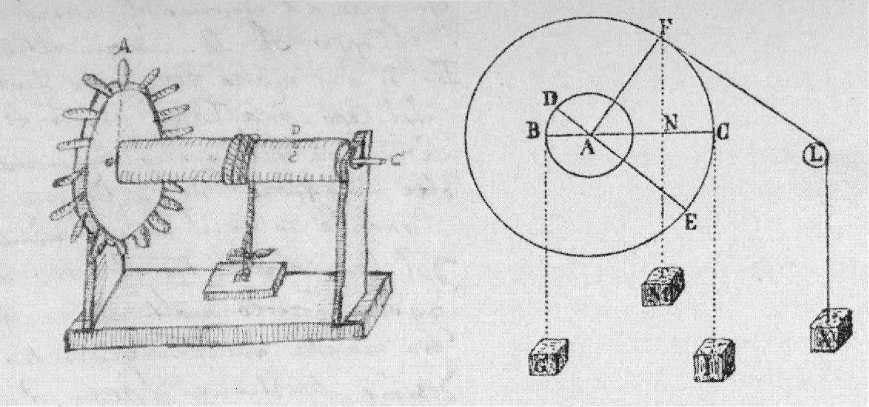
Рис. 8. Практическое описание оси колеса (слева); его геометрическое представление и объяснение, данные Галилеем (справа)

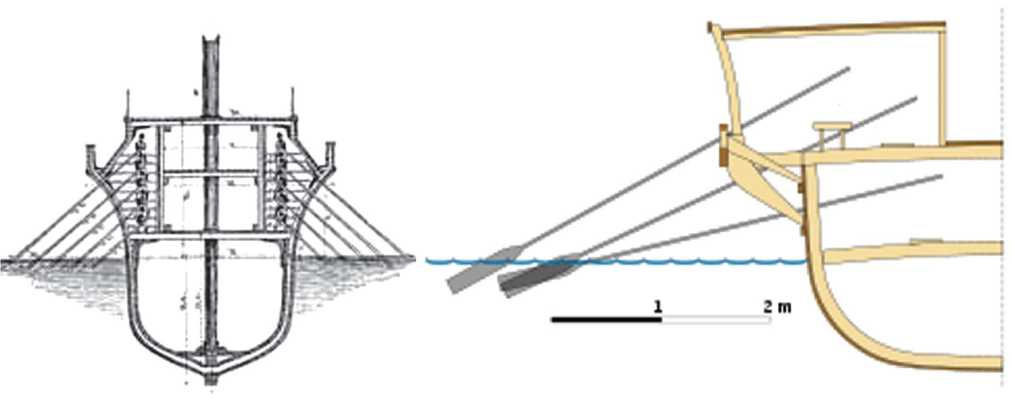
Рис. 9. Quinquireme - квинквирема (от лат. quinquiremis, quinque — пять и remus — весло) или пентера - боевое гребное судно с пятью рядами весел, расположенных один над другим или в шахматном порядке (слева); трирема (справа)

ская кинкерема (пентера) (рис. 9) более эффективна для ведения военных действий в новых условиях использования тяжелой артиллерии, чем традиционно использовавшаяся трирема [5].

Фаусто получил в свое распоряжение команду мастеров-кораблестроителей и венициан-ские верфи, а также необходимое финансирование для строительства нового корабля. Этот факт показывает, каким образом тогда причудливо сочетались теория и практика, гуманитарная традиция возрождения античного наследия и практический опыт современных мастеров-инженеров. Точно также и Галилей взялся за решение аналогичных проблем судостроения (расчет весла тяжелой галеры), едва ознакомившись с практическими познаниями вени-цианских кораблестроителей, которые старался привести в теоретическую форму с помощью все тех же аристотелевских «Механи ческих проблем». Даже если эта работа и не была написана самим Аристотелем, она была выдержана в его духе, и концептуальный аппарат аристотелевской физики, модифицируемый под практические технические проблемы, встававшие перед ренессансными мастерами-инженерами, лег в основу новой Галилеевой науки и был адекватно воспринят практиками и политиками. Галилей был призван в Военно-морской комитет Веницианского арсенала в качестве ученого-эксперта, вооруженного знанием именно «Механических проблем». Но и модели практических инженеров описывались в тех же аристотелевских терминах.

В сущности, перед Галилеем как научным консультантом Веницианского арсенала по вопросам военного кораблестроения была поставлена вполне конкретная инженерная задача, а именно: как оптимально сконструи-

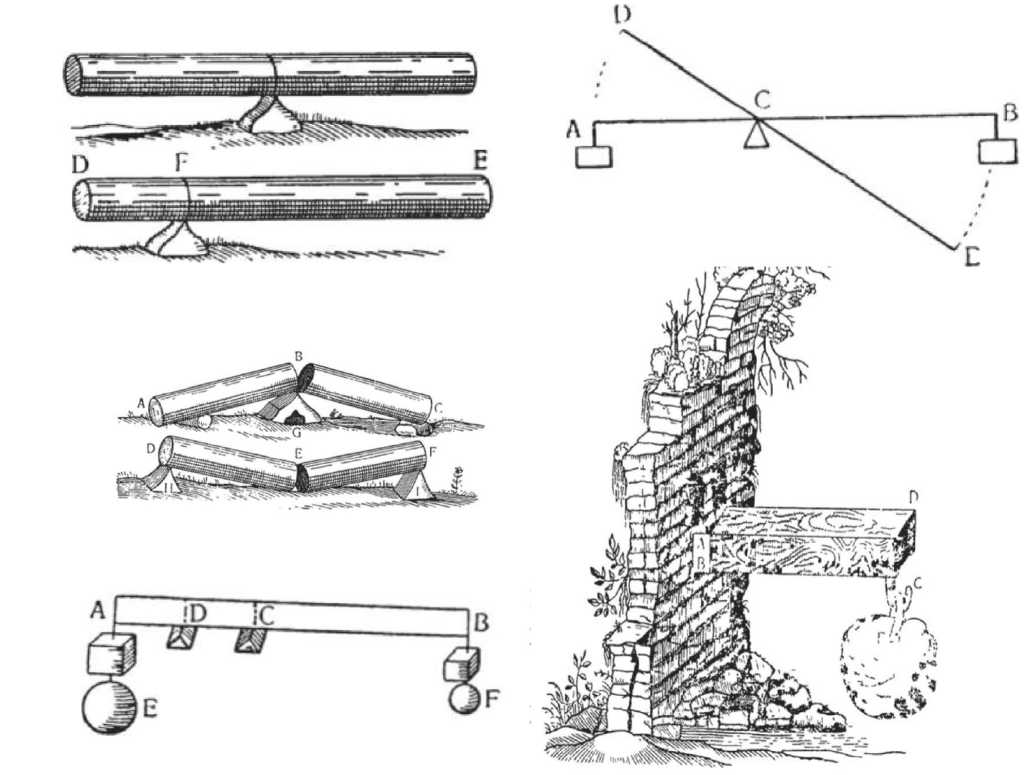
Рис. 10. Модель идеальной балки-консоли Галилея, использованная им для расчета нагрузки на весла галеры

ровать весло для галеры нового типа, т.е. вооруженной тяжелой артиллерией. Эта задача была важной и в социальном плане. От ее решения зависела маневренность корабля и его управляемость, а также риск поломки весла, которое могло не выдержать нагрузки. Галилей в своих «Беседах и математических доказательствах» поставил вопрос о прочности тел, анализируя сопротивление, оказываемое твердыми телами силе, стремящейся их сломать: «Мы получили уже столько выводов, касающихся вопросов сопротивления твердых тел излому, причем в основание этой науки было положено сопротивление тел разрыву, что можем теперь последовательно подвигаться вперед, открывая все новые и новые соотношения, которых в природе существует бесконечное множество, и давая им доказательства» [1, с. 230].

Решая эти задачи, Галилей сначала вслед за аристотелевскими «Механическими проблемами» рассматривает модель весла в виде простого рычага. Однако затем под влиянием опыта корабелов он констатирует тот факт, что весло не может быть рассмотрено в виде простого рычага, поскольку в данном случае важно учитывать как движущую силу, так и то, что сопротивление и опора на галере также находятся в движении. Причем и вода рассматривается им как точка опоры рычага и, кроме того, не статически, как у Аристотеля, а как движущийся водный поток. Отсюда следует вывод, что чем глубже лопасть весла находится в воде, тем больше движущей силы гребец сообщает движению корабля.

Однако такие абстрактные теоретические рассуждения не удовлетворяли практических инженеров, и Галилей вынужден был об ратиться к их опыту, чтобы продвинуться дальше в решении поставленной проблемы. А этот опыт диктовал определенные правила и ограничения в конструировании весел. Тогда Галилей развивает новую теоретическую модель закрепленной на одном конце идеальной балки-консоли. Поскольку весло имеет, по Галилею, две опорных точки (в уключине весла и в воде), он исследует также балку, лежащую на двух опорах [1] (рис. 10). Таким образом, отвергая основные положения аристотелевской физики, Галилей тем не менее использует созданный Аристотелем концептуальный аппарат и некоторые теоретические схемы.

Приобретенный у корабелов опыт Галилей успешно использует и для объяснения космических явлений, например круговращения Земли, которое отрицалось как невозможное. Опираясь на по- лученные при обсуждении проблемы конструирования весел знания, он пишет в «Пробирщике», доказывая, что такое движение Земли согласуется с природой: «...любое тело, если его поместить в разраженную и жидкую среду, которая будет служить его опорой, при увлечении потоком в круговращение по большому кругу самопроизвольно начнет вращаться вокруг себя в направлении, противоположном направлению несущего движения» [3, с. 191].

Одной из наиболее обсуждаемых тогда технических задач была проблема создания вечного двигателя - perpetuum mobile. Многие твердо верили, что искусные инженеры - механики и гидравлики - способны «перехитрить» или даже «перебороть» саму природу. Это убеждение выливалось в своего рода социальное движение, стремившееся упрочить положение инженеров в обществе в противовес тем, кто занимался «естественной философией» и утверждал, что природа доминирует над техникой. Галилей формулирует третью позицию в вопросе соотношения науки и техники, которая становится фактически определяющей в новом естествознании: «Законы природы и законы механики принадлежат к одной и той же области явлений» [6, р. 197, 200-203]. Именно эта позиция легла в основу всего последующего развития естествознания и научной техники, высшей формой выражения которой стали технические науки.

Таким образом, научное инженерное образование имеет свою предысторию, уходящую корнями в эпоху на рубеже Ренессанса и Нового времени. Первый опыт научного образования инженеров мы находим именно у Галилео Галилея. С развитием и повсеместным внедрением огнестрельного ору жия ситуация в военной области резко меняется. Говоря современным языком, на первый план выходит военно-промышленный комплекс. Военные инженеры, составлявшие тогда инженерную элиту, в условиях появления и развития тяжелой мобильной пороховой артиллерии больше не могли полагаться на простой неотрефлекти-рованный опыт и интуицию. Им были нужны точные расчеты. Артиллерия и фортификация сами становятся сложной, основанной на математике наукой. Галилей интегрирует практические и теоретические знания, рефлектируя новый тип знаний, полученных в инженерной практике, и корректируя существовавшие теоретические представления. Именно эта его установка приводит к убеждению в необходимости освоения инженерами основ естествознания.

Именно ученые-инженеры были реальным центром того культурного сдвига, о котором мы говорили в начале статьи. Как раз таким инженером и был Галилео Галилей: «Его хорошее чутье в сфере бизнеса и прекрасные коммуникационные навыки сделали его одним из наиболее популярных инженеров-ученых своего времени... Величие его науки, однако, было следствием ее связей с практическим знанием» [6, р. 211]. Следовательно, уже тогда инженерное образование, как и теперь, служило стимулом для теоретической систематизации практических знаний.