Ударноволновой механизм образования оптических импульсов высокой пиковой мощности

Феномен возникновения ударных волн огибающих для лазерных импульсов впервые был исследован Л.А. Островским приблизительно 50 лет назад [1, 2]. В этих работах было показано, что зависимость групповой скорости от интенсивности распространяющегося в среде мощного лазерного импульса приводит к нелинейной трансформации его формы и увеличению крутизны его фронта (заднего или переднего в зависимости от знака параметра дисперсии керровской нелинейности). В результате может происходить генерация ударной волны огибающей лазерного импульса, что принципиально напоминает процесс образования ударных волн в акустике [3].

Динамика образования ударной волны огибающей в нелинейных средах достаточно подробно рассматривалась во многих работах [4-12]. Вместе с тем, появление новых оптических материалов – фотонно-кристаллических световодов [13-15] и композитных материалов с гигантскими нелинейностями, реализующих условия плазмонного резонанса [16-18], делает актуальным рассмотрение динамики мощных лазерных импульсов в средах с высоким параметром самообо-стрения. В волноведущих системах этого типа параметр самообострения может принимать ги-

гантские, по сравнению с “обычными” оптическими материалами (например, кварцевыми волоконными световодами), значения. Кроме этого в работе будет рассмотрен вопрос о реализации волновода, имеющего не только положительный, но и отрицательный параметр самообострения, который приводит к укручению переднего фронта лазерного импульса (в отличие от положительного, деформирующего задний фронт).

Получение ударных волн с высокой крутизной переднего фронта может представлять значительный практический интерес. Так, в одной из первых методик сжатия мощных лазерных импульсов [19, 20] в качестве компрессоров предполагалось использовать обычные оптические усилители в сильно инвертированной активной среде. При этом использование подобной схемы оказалось затруднительным, поскольку если импульс имеет пологий фронт, усиление всей передней части вводимого в усилитель импульса не только не приведет к сжатию, а наоборот, может привести к существенному его уширению. В силу этого, для сжатия импульса перед усилителем размещают устройство (например, ячейку Керра или Поккельса), срезающее фронт вводимого в усилитель импульса. Таким образом, для сжатия импульса в процессе усиления весьма желательно отсечь слабые участки его переднего фронта, чтобы они не истощали активную среду до прихода максимума огибающей. Для этого важно с самого начала придать переднему фронту импульса “ступенчатую” форму, тогда именно передняя часть импульса будет получать большую часть энергии, запасенной в усилителе. В результате, можно говорить о том, что возможность получения ударных волн на переднем фронте импульса позволяет обходиться без дополнительных обрезающих устройств, при реализации режима совмещающего усиление и вре- менное сжатие для мощных лазерных импульсов в активной среде.

Отдельно следует упомянуть, о связанном феномене, привлекающем в последнее время большое внимание - волновых пакетах, получивших в литературе название “rogue wave” [21-24]. Их отличительной чертой принято считать, в том числе, деформацию волнового фронта (т.н. эффект “оптического цунами” [25,26]). Все вышесказанное демонстрирует важность исследования динамики мощных лазерных импульсов в средах с нестандартно высоким значением параметра само-обострения, способного приобретать как положительные так и отрицательные значения.

• 2.    ОБЩАЯ МОДЕЛЬ ВОЗНИКНОВЕНИЯ УДАРНЫХ ВОЛН В НЕОДНОРОДНЫХ СВЕТОВОДАХ

Распространение волнового пакета в оптической среде с керровской нелинейностью описывается уравнением [27]:

5 ² E   1 5 ² E     5 ² P       5 ² P_w

+ A     = - A   NL", (1)

5 z ²     c ² 5 t ^{2      0} 5 t ^{2         0} 5 t ² ’ ⁽ )

Здесь E ( z , t ) - электрическое поле пакета, которое может быть выражено через комплексную медленно меняющуюся амплитуду E ( z , t ) = | A ( z , t )|exp [ i ( ( в ( ® , z ) - в о ) z - ( a - « 0 ) t ) ] , P_L и P_NL – линейная и керровская нелинейная составляющие поляризации соответственно, Д> и to ₀ - постоянная распространения и несущая частота пакета. Для волновых пакетов с длительностью т ₀ <<  T _NL справедливо следующее выражение для нелинейной керровской поляризации:

PNL = 2 ^0 Z(3) I Al2 A exp(i(Д,z - ^0t)) , где тNL - характерное время нелинейного отклика среды, х(3) -керровская диэлектрическая восприимчивость. В первом порядке малости по параметру тNL / т0 нелинейный источник в (1) имеет вид [28]:

t^ =- 2 <  [ л A² A ^{- i} [ 2£ - ^ ]d t ⁽| A= A ^( д zt y , . (2)

Введем радиальное распределение поля U ( r ) в волноводе в плоскости поперечной к направлению распространения ( m – азимутальный индекс моды) [29]

E ( r , t ) = E ( z , t )U ( r , ф ) = U ( r ) cos( т ф ) A ( z , t ) exp ( i ( в ₀ z - ® 0 1 ) )

Поперечный профиль поля моды U(r) удовлетворяет волновому уравнению d2 U 1 dU

+ dr r dr

m

r

U

= ⁰ . (3)

Через распределение U ( r ) определим параметр S_ef – эффективную площадь моды

S ef

= 2 n J | U ( r )|² rdr

^ да                  Л

/ J | U ( r )| ⁴ rdr

10            7

В дальнейшем подразумевается, что мы рассматриваем распространение пакета в одномодовом азимутально-симметричном случае m = 0 . В общем случае этот параметр может изменяться по длине волновода S ef ( z ) . Введем также следующие обозначения, которых будем придерживаться в дальнейшем:

3 v (³⁾         i^^m

• (2)    _ ³ Л n -     ^Ш 0

= -----, ^ =-----

8 n          cSef

Здесь n – линейный показатель преломления среды, n<2) - параметр кубической керровской нелинейности, R – коэффициент нелинейности, выраженный в Вт-1м-1, который также может зависеть от z . При помощи стандартной процедуры [27, 28] из уравнения (1) может быть получено уравнение для медленно меняющихся амплитуд A(z, t), которое в сопутствующей системе координат, движущейся с групповой скоростью ug (z) = (5в / 5^)2= т0, имеет вид dAJD d^A ~д2 Ч дт^

+ i^ l A I² A + A

5 т

(I A|² A ) = 0 , (4)

где т - время в сопутствующей системе координат

z т = t-Jdz/Ug(z),    D(z) = (52в/5^2);=й0 - дисперсия групповых скоростей (ДГС). Важную роль в дальнейшем будет играть параметр само-обострения Ц (в англоязычной литературе selfsteepening), в общем случае также зависящий от продольной координаты z , который можно записать в виде [28, 30]

2 n ⁽²⁾

Ц =--- cS ef

(2) to ₀  5 n

с d®\ Sef 7

При учете члена, связанного с этим параметром, к групповой скорости волны возникает нелинейная добавка, пропорциональная второму слагаемому в

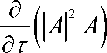
= A

5| A l *

5 т

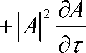
Зависимость групповой скорости волны от ее амплитуды является характерной чертой образования ударной волны огибающей. При Ц > 0 максимум огибающей импульса распространяется со скоростью, меньшей групповой скорости волнового пакета ug в среде, что означает сме- щение максимума в хвост волнового пакета, в результате чего происходит его укручение. При p < 0 возможно образование ударной волны на фронте импульса.

Поясним сказанное известным примером [4], в котором пренебрегается дисперсионными эффектами. Это приближение вполне корректно для достаточно длинных оптических импульсов c шириной спектра

^pp 0 ^ ⁰ ) скорость максимума огибающей совпадает с групповой скоростью импульса.

Для определения формы импульса в нелинейной усиливающей среде соотношение (8) удобно представить в виде

Q

— <<

^Т 0

p л|2

D

Представим решение уравнения (3) в виде

A ( z , t ) = р ( z , t )exp ( i ф ( z , t ) ) , (6) где р и ф - действительные амплитуда и фаза волнового пакета. Пренебрегая в уравнении (4) дисперсионным членом и разделяя действительную и мнимую части, получаем для амплитуды волнового пакета следующее уравнение:

z т = 3Р2 J p(^>d^ + т0д/21п(Р01 p) , (11) 0

где знак “–” относится к фронту импульса, а знак “+” к хвосту. Укручение фронта импульса, в конечном итоге, приводит на некоторой длине L_B к образованию разрыва, которому отвечает |др д Т ^ да , т.е. формируется ударная волна огибающей. Из соотношения (11) можно получить следующую неявную связь длины образования ударной волны L_B с параметрами световода и вводимого импульса:

L_B J 0

p ⁽ z ) dz = sign ( ^{p T 0} e 2 /2 3 p 0

дР Л 2 5 р „ — + 31 p ( ^ ) d ^p — = 0 д z • дт ^.

Из которой, в случае однородного усилителя p = const , можно получить известное выражение [28]:

Проанализируем решение полученного уравнения (7) на примере начального импульса гауссовой формы:

L B

т ₀ V e /2

³| ^p P 0 •

т ²

Р ^{( т ,0)} = Р о ^ехР^(- —т).

^{2 т} о

Решение уравнения для амплитуды р ( т , z ) , определяющей форму импульса, можно записать в неявном виде:

Следует отметить, что все полученные выше результаты могут быть использованы и для активного волновода с усилением g ( z ) , описываемого уравнением

дЛ-iD 52A az Ч "Т?

+ iR\A\" A + p 0°-(| a² A ) = gA . (12)

Р ^{( т} , ^z ) = Р о ^ехР

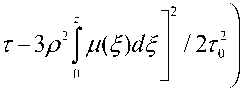
. (8)

В этом случае уравнение (3) с эффективными коэффициентами

С учетом определения времени в бегущей системе координат для средней по длине z скорости максимума огибающей волнового пакета u_m верно соотношение

R ( z ) = R ( z ) exp

(z        ^

2 J g ( # ) d §

I 0         J

u m = z

\ —1

z                     zi

J u;'(^) d^ + 3 p2 J p (^) a-.

о                       0

( z,          )

/ / ⁽ z ) = p ⁽ z ^)exp ² J g⁽ 5 )d ^ .

I 0         J

остается справедливым для амплитуд A ( z , т ) , связанных с первоначальными как

В общем случае величина u_m является сложной функцией координаты z . В частном случае однородного световода (т.е. при p = const , u_g = const ) выражение для скорости максимума огибающей принимает известный вид [4]:

=     u g

1 + 3pugР2 •        (10)

При этом очевидно, что в линейном приближении (т.е. для импульса малой мощности, когда

A ( z , т ) = A ( z , т )exp

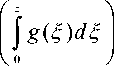
• 3.    ОБРАЗОВАНИЕ УДАРНЫХ ВОЛН В ВОЛНОВОДАХ С ДИСПЕРСИЕЙ.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Приведенные выше соотношения дают принципиальную упрощенную картину образования ударных волн в оптических волноводах. Между тем дисперсия групповых скоростей оказывает существенное влияние на переформирование импульса, описываемого уравнением (4). Даже если на начальном этапе длительность импульса была значительной, и эффектами ДГС можно было пренебречь, при укручении фронта импульса, т.е. при ∂A ∂τ→∞ дисперсионное расплывание начинает играть большую роль. Качественно можно пояснить, что при образовании ударной волны ширина спектра импульса увеличивается, что делает дисперсионные эффекты более значимыми. Дисперсионный разброс скоростей приводит к ограничению крутизны фронта импульса.

Известны точные решения уравнения (4) с постоянными коэффициентами, описывающие распространение кинков (“ступенек”) излучения [5], и импульсов солитонного вида, в пределе µ → 0 переходящих в фундаментальные солитоны нелинейного уравнения Шредингера (НУШ) [6-8]. Точные аналитические решения для импульсов с энергиями большими энергии фундаментального солитона, т.е. в случае ρ 02 > D R τ 02 неизвестны, поэтому приходится ограничиваться численным решением уравнения (4). Нами проведен численный анализ эволюции начального импульса A 0 ( t ) = P 0 cosh( ττ 0 ) с длительностью τ 0 = 25 пс и мощностью ю-ю₀, I О¹² с¹

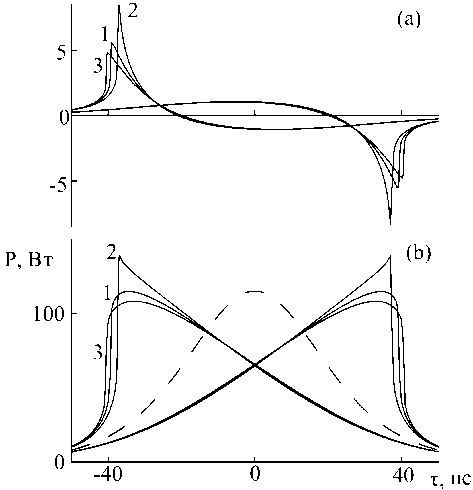
Рис. 1. Образование ударной волны:

(а) Изменение мгновенной частоты;

(b) огибающие импульсов после распространения в волноводе длины 10 м, с параметрами R = 0.05 Вт ^{- 1}м ^{- 1}, µ =- 10 ^{- 14}Вт ^{- 1}м ^{- 1}с, 1 – D = 0, 2 – D =- 7 ⋅ 10 ^{- 26}с²м ^{- 1}, 3 – D = 5 ⋅ 10 ^{- 26}с²м ^{- 1}.

Симметрично показаны результаты для волновода с µ = 10 ^- 14 Вт ^- 1 м ^- 1 с . Штриховой линией показана огибающая начального импульса

P 0 = 115 Вт в волноводе с аномальной ( D <  0 ) и нормальной ( D >  0 ) дисперсией. Результаты показаны на рис. 1, 2. Там же указаны параметры волновода. Отмечаем, что для моделирования использовались как положительные, так и отрицательные значения параметра самообострения | µ = 10 ^- 14 Вт ^- 1 м ^- 1 с . Возможность получения столь высоких значений µ разных знаков в фотонно-кристаллических (ФК) волноводах обсуждается ниже, в следующей части работы. Добавим также, что используемые здесь и далее значения параметров нелинейности R и дисперсии D несколько превосходят стандартные величины для кварцевых волокон, но вполне достижимы в ФК волноводах. Для сравнения приведены также результаты в бездисперсионном случае.

Как можно видеть из рисунков, импульс в ходе распространения приобретает асимметричную форму с образованием крутого переднего или заднего фронта в зависимости от знака µ . Спектр импульса (рис. 2) значительно уширяется в сторону высоких или низких частот также в зависимости от того, ускоряется максимум импульса ( µ < 0 ) или замедляется ( µ > 0 ). Из сопоставления с графиком мгновенной частоты (рис. 1 (а)) видно, что уширение спектра связано со смещением частоты наиболее крутой части фронта импульса. В области нормальной дисперсии фронт смещается дальше от первоначального центра импульса, но его частотный сдвиг ниже, чем в области аномальной дисперсии. При аномальной дисперсии положение максимума сдвига частоты близко к положению максимума им-

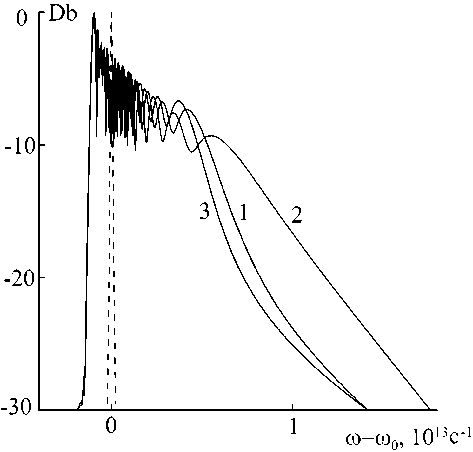
Рис. 2. Спектр ударной волны при укручении переднего фронта импульса прошедшего 10 м волновод с параметрами R = 0.05 Вт-1м-1, µ= -10-14 Вт-1м-1с, 1 – D=0, 2 – D =-7 ⋅10-26 с2м-1, 3 – D =5⋅10-26с2м-1 . Штриховой линией показан спектр начального импульса пульса, что согласуется с аналитическими решениями уравнения (4). Известно, что точные солитонные решения этого уравнения обладают специфической фазовой модуляцией [6-8]

фт = ^(r) = - 2 Д A(т)|2 +Ди , где А и — разность между скоростью солитона и групповой скоростью волны. Таким образом, можно предполагать, что в области аномальной дисперсии на фронте импульса происходит формирование солитоноподобных частотно-модули-рованных импульсов.

Рассмотрим образование фронта ударной волны подробнее. Отметим, что расплывание фронта в случае нормальной дисперсии приближенно можно описать при помощи соотношения для скорости пика импульса (10). Действительно, изменение скорости максимума импульса за счет самообострения А u g □ 3 Ц и₈ P o компенсируется дисперсионным изменением скорости пика, происходящим за счет уширения спектра импульса

du

А и « Аю □ ЗциР.. g   dm         g

С учетом того, что d ( ug ) 1 J d m = D , отсюда можно оценить длительность крутого фронта импульса при нормальной дисперсии

D

^T f □ 3 Д 0 .                ⁽¹³⁾

Несколько по-иному происходит укручение фронта в случае аномальной дисперсии. Известно, что импульс с энергией значительно большей энергии фундаментального солитона ( N -солитонный импульс, N >>  1 ) при распространении в нелинейной среде с аномальной дисперсией, описываемой НУШ, трансформируется в совокупность коротких импульсов близких к фундаментальным солитонам. Это одно из проявлений специфически нелинейного процесса модуляционной неустойчивости [27]. Если по аналогии с НУШ провести анализ уравнения (4) на предмет устойчивости постоянного решения A = A₀ exp( iRAz ) к малым гармоническим возмущениям, то можно получить, что член пропорциональный параметру Д препятствует развитию модуляционной неустойчивости и до некоторых пор стабилизирует целостность импульса. Действительно, коэффициент усиления модуляции на частоте Q = | ю — ю ₀| можно записать как [31]

g ( О ) = 2 Q RDA

v

( I D ^ У v ² V

^{— Д} A 4

1/2

V

. (14)

Он приобретает действительные значения в полосе частот

Q на частоте a = V2 A I R—“ A m       0 V\d\ 2D2 V

.

При высоких значениях Д >

( R D ) ^1/2 A 0

полоса частот модуляционной неустойчивости сужается до 0, и импульс сохраняет целостность.

При распространении импульса и достижении на его фронте значений 5| A] ^Тт ^да спектр импульса резко уширяется (см. рис. 2), и приближение малых гармонических возмущений становится неадекватным. В результате на стыке фронтов импульса образуется область модуляционной неустойчивости и формируется солитоноподобный импульс с пиковой мощностью A_s 2 и длительностью А т <<  Т _п. Величины A ² и Аг мож-

0                 5 т но связать приближенным соотношением

R D A —I D] — Д2 а; = 0, <Ат V которое в пределе Д ^ 0 переходит в определение фундаментального солитона RA^ = D/Ат2 .

Приведенные качественные соотношения подкрепим численным решением уравнения (4) при различных значениях параметров самообос-трения Д и аномальной дисперсии D <  0 . На рис. 3 представлены результаты численного моделирования распространения импульса начального импульса A ₀( t ) = piC cosh( T/ т 0 ) с длительностью т ₀ = 25 ps и мощностью P 0 = 192 Вт в волноводе с указанными значениями параметров D , Д и R .

Рис. 3 (a, b, c) подтверждают вывод о том, что при распространении импульса в волноводе с аномальной дисперсией высокие значения дисперсии нелинейности препятствуют развитию модуляционной неустойчивости. При достаточно высоких значениях Д формирования характерной многопиковой структуры импульса не происходит, однако, огибающая приобретает асимметричную форму. На определенной длине распространения на крутом фронте импульса можно наблюдать образование отдельного пика. На рис. 3 (d, e, f) показана структура импульса с образующимся пиком при различных значениях параметра аномальной дисперсии волновода.

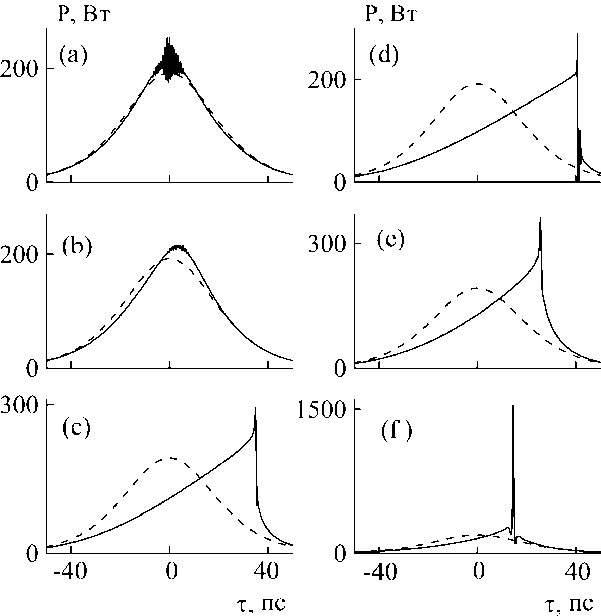
Рис. 3. (a, b, c) Результаты моделирования распространения импульса в волноводе длины 5.7м, с параметрами R = 0.03 Вт ^{- 1}м ^{- 1}, D =- 3 ⋅ 10 ^{- 25}с²м ^{- 1} , (a) – µ = 0 , (b) – µ = 10 ^- 15 Вт ^- 1 м ^- 1 с , (с) – µ = 10 ^- 14 Вт ^- 1 м ^- 1 с ;

(d, e, f) Результаты моделирования распространения импульса в волноводе с параметрами R = 0.03 Вт ^{- 1}м ^{- 1}, µ = 10 ^{- 14} Вт ^{- 1}м ^{- 1}с ,

(d) – D =- 10 ^{- 25}с²м ^{- 1}, l = 7.2м (е) – D =- 10 ^{- 24}с²м ^{- 1}, l = 4м , (f) – D =- 5 ⋅ 10 ^{- 24}с²м ^{- 1}, l = 2.4м . Штриховой линией показана огибающая начального импульса

Как можно видеть, пиковая мощность и энергия формирующегося пика увеличиваются с ростом аномальной дисперсии волновода, что можно объяснить повышением коэффициента модуляционного усиления. В итоге это приводит к повышению отношения энергии пика импульса к энергии его пьедестала и, таким образом, при гигантских значениях дисперсии |D | □ 10 23 C 2 M ¹ позволяет рассчитывать на достижение высокоэффективной компрессии исходного импульса.

Следует отметить также изменение скорости пика по отношению к краю импульса, на котором он образовался. С увеличением своей мощности пик ускоряется (или затормаживается, в зависимости от знака µ ) и проникает внутрь импульса. Таким образом, происходит образование структуры фронта. Этот процесс проиллюстрирован результатами моделирования на рис. 4. Как мо 2 жно видеть, в области высоких значений ∂ A ∂ τ формируется зона модуляционной неустойчивости, наивысшего значения коэффициент модуляционного усиления достигает в точке максимума крутизны. Вследствие меньшей скорости пика эта зона углубляется внутрь импульса, оставляя за собой возмущенный участок.

В зависимости от соотношений между параметрами импульса и волновода этот процесс может происходить устойчиво либо сопровождаться увеличением частотного диапазона модуляционной неустойчивости и резким уширением спектра импульса. В конечном счете, второй вариант приводит к распаду импульса.

Как показывает проведенный анализ, распространение импульсов излучения в волноводах с высокими значениями параметра самообострения µ представляет значительный прикладной интерес. На основе подобных волноводов могут быть получены высокоэффективные оптоэлектронные элементы – компрессоры, излучатели широкого спектра, генераторы импульсов с высоким градиентом мощности. В следующей части работы обсуждаются вопросы, связанные с возможностью изготовления подобных волноводов.

• 4.    ЗНАЧЕНИЕ ПАРАМЕТРА

САМООБОСТРЕНИЯ В ГРАДИЕНТНЫХ ВОЛНОВОДАХ

Как было показано выше, динамика импульса излучения в значительной мере зависит от величины и знака параметра самообострения µ , характеризующего волноведущую среду. Как правило, этот параметр полагается малой и всегда положительной величиной с очень хорошей степенью точности равной ц □ 2R / <У0 и слабо влияющей на динамику волнового пакета в том случае если длительность импульса значительно больше 100 фс, а пиковая мощность значительно меньше 1 МВт. Подобное действительно с высокой степенью справедливо для кварцевых ступенчатых волноводов или для получивших в последнее время широкое применение волноводов с “W”-образным профилем показателя преломления. Однако, с другой стороны, в современных фотонно-кристаллических (ФК) волноводах локализация излучения достигается не за счет полного внутреннего отражения, а за счет брэгговского механизма “запирания” излучения в сердцевине волновода. В этом случае, очевидно, имеется сильная зависимость эффективной площади моды, а как следствие параметра само-обострения и кубической (керровской) нелинейности от несущей частоты.

Выражение (5), определяющее параметр са-мообострения, можно переписать в виде

2 n ⁽²⁾     к₀ Ге n ⁽²⁾ ) k_o n ⁽²⁾ Геs_e/ )

ц =0+        - cSef Sef I д Ш J 8^ ( d Ш J , (15) где k0 = to0 /с. Обычно, при анализе динамики волнового пакета вторым и третьим слагаемыми параметра самообострения пренебрегают, что справедливо для наиболее распространенных волноводов со ступенчатым или “W”-образным профилем показателя преломления. С другой стороны, в работе [30] показано, что в брегговс-ких волноводах с одномерной неоднородностью показателя преломления могут быть получены значения эффективного параметра самообостре-ния существенно выше стандартных. Возможной является и реализация волноводов с отрицательным параметром Ц. Эффекты подобного рода, связанные с резким увеличением величины и изменением знака параметра самообострения, могут наблюдаться и в ФК световодах с 2D структурой изменения показателя преломления. Кроме того, в качестве волноведущей среды с высоким по модулю значением параметра самообостре-ния, могут быть предложены среды с высокой дисперсией керровской нелинейности, например, композитные материалы, описываемые соотношением Максвелла-Гарнетта [18].

Следует отметить, что сильная дисперсия площади моды потенциально сопряжена с неустойчивостью распространяющегося волнового пакета, при которой даже незначительные дефекты в параметрах среды приводят к резкому росту оптических потерь. Таким образом, спектральные диапазоны обеспечивающие большие значе- ния параметра самообострения, как правило, не используются в виду большой чувствительности к вариации параметров чреватой большими оптическими потерями. Тем не менее, для ФК сред с большими кубическими нелинейностями соответствующие диапазоны могут быть использованы для эффективного управления формой огибающей импульсов.

Рассмотрим типичный случай, в котором может быть показана существенная зависимость параметра самообострения от параметров волновода, на примере волновода с параболическим профилем. Показатель преломления сердцевины “стандартного” волновода описывается соотношением [29]

n ( r ) = n 1

⁰ ^ r ^ r 0 , (16)

а показатель преломления оболочки

n(r) = n1 (1 -Д)1/2, r > r0, где Д = (n2 - n2)/n , n1, n2 - показатели преломления материалов световода. При g = 1 волновод обладает треугольным, при g = 2 параболическим профилем показателя преломления. Большие значения показателя g соответствуют волноводу со ступенчатым профилем показателя преломления.

Для получения дисперсионных зависимостей параметров основной моды волновода получим решение волнового уравнения (3) в гауссовом приближении [29]. В соответствии с ним радиальное распределение поля моды можно записать как

U(r)2 = exP(-r2 / 2w2), где w =(Sef/П) - радиус поля моды. Константа распространения связана с радиальными распределениями моды и показателя преломления соотношением го j (k2 n2 (r)U2 - (dU/dr )2) rdr 20

^e = го , (17)

j U2 rdr здесь k = k0ni. Из уравнения др2 [дw = 0, получаем дисперсионную зависимость радиуса моды w2 = 2 r0/ k 7Д.              (18)

Таким образом, эффективная площадь моды волновода определяется как S ef = 2 n r ₀ / k\ Д .

Вычисляя интегралы в (17), получаем выражение для константы распространения LР01-моды в волноводе с параболическим профилем показателя преломления

2 Уд) 1/² kr ,

Поскольку параметр Д <<  1 , то при рассмотрении поставленной задачи можно считать, что в = к 0 п 1 , и поэтому групповая скорость и ДГС не зависят от диаметра волновода и постоянны по всей его длине. В этом случае, для волновода с параболическим распределением показателя преломления можно записать выражения для коэффициента керровской нелинейности

R = к02 п(2) УД /2пг0, и параметра самообострения (согласно (15))

k „7Д Г ₍₂₎       дп^<2>      ₍₂₎ д п ю пп ⁽²⁾ дд)

ц = -° пп -Щ Д Щ Д   1  0-1

п-0c (          г®       дю    д  г®J. (19)

Отметим, что даже в рассмотренном случае волновода с параболическим профилем параметр самообострения Ц может значительно отличаться от стандартного приближения □ 2 R / ю ₀ из-за наличия дисперсионных слагаемых. При этом знак Ц может быть как положительным, так и отрицательным.

В отличие от параболических волноводов, широко распространенные волноводы со ступенчатым профилем показателя преломления обладают слабой дисперсией площади моды. Сравнить их дисперсионные характеристики можно при помощи известной формулы Маркузе [32]. Эта формула с высокой точностью описывает зависимость радиуса волноводной моды w от волноводного параметра wA BC

,0 ~ V 2м+g)+ V+V6, где V = —(п2 - п2)1/2, c

где g – параметр профиля показателя преломления из (16). Для ступенчатого световода g ^ да , и численные коэффициенты в (20) определяются как A = 0.65, B = 1.619, C = 2.879 . Его дисперсионная зависимость показана пунктиром на рис. 5. Как можно видеть, в области “рабочих” значений r ₀ >  2 Л для таких волноводов W □ r ₀ . Сравнивая этот результат с (18), отмечаем, что дисперсия площади моды у ступенчатых волноводов практически отсутствует (нет зависимости площади моды от k ).

Рассмотрим теперь волновод со структурой поперечного сечения, характерной для ФК волокна. Как показано в работе [33] формула Маркузе (20) описывает дисперсионную зависимость площади моды и в этом случае. При этом волноводный параметр следует определить как

V PCF

2 п Л А

( п. - п_я ) ^1/2

где n_eff – эффективный показатель преломления структурированной оболочки световода. Рассмотрим типичный пример ФК волокна (см. вставку на рис.5). Центральная часть световода, служащая его сердцевиной, окружена оболочкой с гексагональной системой воздушных отверстий диаметром d , отстоящих друг от друга на расстояние Л. n_eff определяется как эффективный показатель преломления основной моды беско-

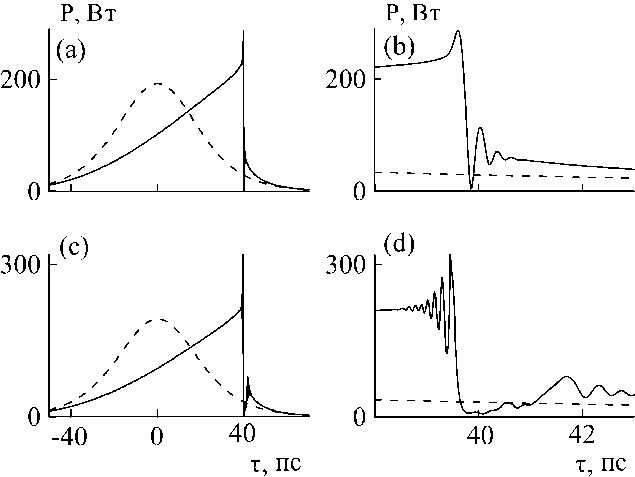
Рис. 4. Результаты моделирования распространения импульса в волноводе с параметрами R = 0.03 Вт ^{- 1} м ^{- 1}, D = - 1.5 - 10 ^{- 25}с²м"1, Ц = 10 ^{- 14} Вт ^{- 1}м^-1с , (a, b) l = 6.6 м , (c, d) l = 7.5м .

Штриховой линией показана огибающая начального импульса

О 12   3   4   5   6

NX, г0 /X

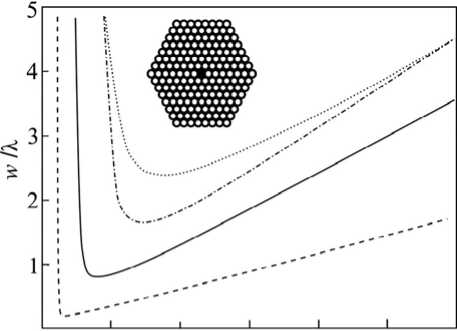
Рис. 5. (Взят из [34]). Зависимость радиуса волноводной моды кварцевого структурированного световода от постоянной структуры л , рассчитанная с помощью аппроксимации (21) для Л = 1 мкм, d Л = 0.3 (штрихпунктирная линия), 0.5 (сплошная линия), 0.9 (штриховая линия). Пунктирной линией представлена зависимость радиуса волноводной моды от радиуса сердцевины r 0 для стандартного ступенчатого световода с n 1 — n ₂ = 0.01.

На вставке – изображение поперечного сечения ФК световода нечной гексагональной периодической структуры с воздушными отверстиями диаметром d и периодом Л. Формула (20) с коэффициентами A PCF = 0.7078, B PCF = 0.2997, C_PCF = 0.0037, g = 8 обеспечивает высокую точность аппроксимации зависимости отношения w[Л от параметра V_PCF

w

Л

A R

PCF      PCF

2/(2+ g )        3/2

VPCF     VPCF

с

+ PCF

PCF

На рис. 5 (взят из работы [34]) приведены зависимости радиуса моды от постоянной Л для ФК волноводов с гексагональной структурой при различных значениях отношения d/Л. Отметим то, что область дисперсионной зависимости радиуса моды ( w х Лn, n ^ 1 ) находится в допустимых пределах для современных ФК световодов, реализующих локализацию излучения за счет брег-говского механизма. С увеличением пористости структуры оболочки эта область смещается в зону значений Л порядка длины волны для dЛ □ 0.5. Таким образом, следует обратить внимание на то, что в спектральных областях, находящихся вблизи брегговского синхронизма, дисперсия эффективной площади моды может достигать очень высоких значений. Отметим также то, что слева от точки минимума площади моды имеется зона большой и при этом отрицательной дисперсии площади моды, т.е. —5Sf / dto >> Sf I to. Из-за сильного изменения площади моды и связанного резкого увеличения оптических потерь соответствующий спектральный диапазон используется довольно редко, однако, как видим, он может найти применение для получения волноводов с гигантской по модулю дисперсией нелинейности. В этом диапазоне параметр самообостре-ния ФК волноводов может принимать как положительные, так и отрицательные значения по модулю более чем на два-три порядка превосходящие стандартные.

• 5.    ЗАКЛЮЧЕНИЕ

В работе обсуждается динамика оптических импульсов в волноводах, характеризующихся высоким значением параметра самообострения Ц . Актуальность работы связана с тем, что эволюция импульсов в волноводах этого типа приводит к возникновению волн с высоким градиентом мощности, востребованных в широком круге приложений. Подробно рассматривается процесс образования ударной волны огибающей на переднем фронте (при Ц <  0 ) и в хвосте импульса ( Ц >  0 ) как в бездисперсионном случае, так и при наличии нормальной и аномальной дисперсии волновода. В работе показано, что при высоком параметре самообострения модуляционная неустойчивость импульсов, распространяющихся в нелинейной среде с аномальной дисперсией, снижается, тем не менее в зоне наивысшего градиента мощности этот нелинейный эффект приводит к образованию солитоноподобных пиков. При высоких значениях аномальной дисперсии, таким образом, можно говорить об эффективной ударной компрессии импульса и достижении высоких пиковых мощностей излучения. Рассмотренный ударноволновой механизм может найти применение и при генерации излучения с широким спектром.

В работе также показана возможность реализации волноводного режима с высоким по модулю как положительным так и отрицательным параметром самообострения. Этот режим может быть получен в фотонно-кристаллических волноводах в диапазоне длин волн близких к параметру структуры оболочки ФК волокна.

Настоящая работа выполнена при поддержке Министерства образования и науки РФ в рамках федеральной целевой программы “Научные и научно-педагогические кадры инновационной России” на 2009-2013 годы.