УДК 539.38; 531.36 напряженно-деформированное состояние осесимметрических деталей и узлов в квазистатических условиях нагружения

Квазистатические условия нагружения деталей многих машин и механизмов, например газодинамических импульсных устройств [1], характеризуются наличием значительных сил инерции, действующих в объемах деталей, величина которых пропорциональна [2] плотности рассматривае-

Л Л d'{u}/ мого элемента р и его ускорения / rTf2 .

В отношении деформационных ускорений речь идет об увеличении внутренних сил, характеризуемых напряжениями {^} , вели- чина которых возрастает пропорционально коэффициенту динамичности к > 1,0 , так что .

Рассмотрим общую схему нагружения элемента газодинамического импульсного устройства –корпуса радиальными ри осевыми р поверхностными силами, движущегося с ускорением под действием силы р (рис.1). Тогда внутри корпуса и его наполнения будут возникать силы инерции ^ИЕ, пропорциональные перечисленным физическим величинам, а присоединенные к данной системе элементы можно будет учесть поверхностными силами, пропорциональными массе и ускорению движения системы в целом, так что

^ИН,Еф тЕф " /^£2 ^ " Рд " 5 , (1)

где: ГОкр иm – массы присоединенного эле- мента (крышки) и всей системы соответственно; s – площадь наибольшего попереч-

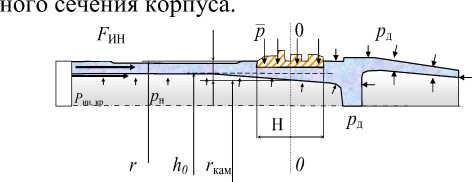
Рисунок 1 – Схема нагружения наполненного корпуса

Здесь: Ря – радиальное давление на полнения корпуса p     c •О , МПа, где:

н1-Цcz ц c  коэффициент Пуассона материала на- полнения (для абсолютно жесткого тела /Vc =0,    а для жидкого    цc=0.5);

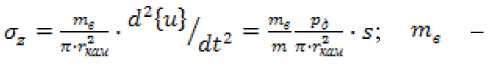
масса наполнения, расположенного выше рассматриваемого поперечного сечения корпуса; ^мм радиус каморы корпуса (рис.1.).

Как правило, корпуса в процессе функционирования таких изделий нагружаются значительными внешними силами, приводящими к конечным пластическим деформациям при значительном формоизменении обтюрирующего кольца (ОК), под действием радиального давления Р и малым упругим или упруго-пластическим деформациям самого корпуса и его наполения.

Для корпуса цилиндрической формы, испытывающего упругие или упругопластические деформации известны зависимости для радиального прогиба W от действия радиальной силы p , полученные Ильюшиным А.А., которые в случае малых деформаций можем выразить суммой составляющих от действия каждой приложенной внешней силы:

W W^p  W^{p д}  ( W^{F ин}   W^{p н}) , (2)

где:

W ₂ ^p   A p и W ^p A p B     (3)

в случае упругой и упругопластической деформации соответственно:

^W 2 ^{p д}

p д     e кор x

кор

r ,   a ₀,

W ^p

н

2 k д

2 p н

cos _cт x ;

кам

кам

r ²;

_{W 2} F ин       _{p д}

E

_A  dW 2 ^p

r2

22 кам

H

m в _; m

3 a

^{d p} E 2 h 0

H  3 a a

_A     00

E   2h  2h a0 k

E 1 k

k кор (1    ² )           E

_{4 E I}    ^; кор   ₂

_I     ^{r 2   4 r r} кам    ^r к ² ам

36 ( r r )

кам

a ₀ 2 h 0 ^;

фициент разупрочнения и модуль упругости материала корпуса соответственно ( 0,95 для корпусов, изготовленных из углеродистой стали с последующей термической обработкой «закалка + высокотемпературный отпуск»).

Зависимости (2 – 4) для корпусов имеющих значительные отличия по геометрии от гладкостенного цилиндра приводят к значительной погрешности результатов расчетов, однако необходимы для построения имитационной модели функционирования изделия более высокого уровня.

Более точное решение можем получить методом конечных элементов (МКЭ), которым возможно учесть геометрию изделия практически с любой наперед заданной точностью. Основной трудностью при этом является принятие той или иной физической модели деформируемых элементов (расчетной области).

Для получения решения МКЭ с использованием практически любых доступных программных средств (2 – 5) можем ограничиться упругопластической постановкой задачи. Тогда расчетная область (рис.2) будет представлена пространством, занимаемым корпусом и его наполнением.

1 k

₁ h 0

2 a ₀

г —г кам

r3

;

;

;

;       (4)

h ₀    радиусы наружной, срединной

поверхностей и толщина стенки корпуса изделия в зоне ОК соответственно; H ширина ОК; x координата положения ОК относительно донного среза корпуса; _s предел текучести материала корпуса; k коэффициент, учитывающий непрямолиней-ность распространения пластической деформации в стенках корпуса ( k =0,9 среднее значение для тонкостенных корпусов, k *0,94 - для толстостенных); X, Е - коэф-

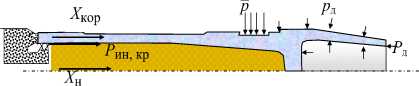
исунок 2 – Расчетная схема

Р

Здесь давление p в проточке корпуса, введено в расчетную схему как результат действия обтюрирующего кольца (ОК), испытывающего конечное формоизменение; ,   – объемные силы в материале кор пуса и его наполнения соответственно.

Схема дискретизации расчетной области для решения задачи МКЭ [3] представлена на рис.3. Сущность МКЭ заключена в исследовании системы линейных уравнений, записанной относительно узловых смещений    сетки конечных элементов, в виде:

,                (5)

где:                                     мат рица жесткости системы, включающая осо-

бенности геометрии, граничные условия, и физические уравнения расчетного объема (постоянные в каждой подобласти, определенной материалом детали). В случае идеального упругого изотропного тела физиче- ские уравнения соответствуют закону Гука:

1x1    1x1 (1x3

{" . } = A '  B n

6x1 бхб 1^6x4

3x1    1x1   1хГ

U n }-{« T }-{£⁰} 4x1    6x1   6х1_?

где A - матрица упругих констант в случае изотропного материала и осесимметриче- ского тела в цилиндрических координатах:

A h E ⁽¹-^

1  1   (1 + ц).(1-2-ц)

Ц /1-ц W / 1-ц

W	ц/	0
Л-ц	Л-Ц
1	ц/ Л-Ц	0
ц/ Л-Ц	1	0
0	0	1-2-ц/
		/2-(1"Ц)

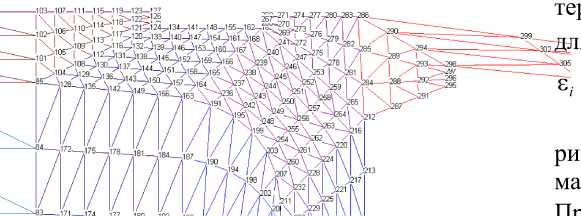
Рисунок 3 - Пример автоматического разбиения на конечные элементы ( фрагмент нумерации узлов в зоне возможных концентраций напряжений)

По физическому смыслу уравнение (5) представляет собой уравнение равновесия системы (в перемещениях). Для получения единственного решения система должна быть дополнена граничными условиями в перемещениях.

В большинстве задач динамического нагружения применение модели идеально упругого тела для расчета корпуса и некоторых других элементов системы невозможно, поскольку они могут испытывать пластические деформации. Это приведет к физической нелинейности уравнения (5).

Пусть условие перехода материала в пластическое состояние определяется на основании поверхности текучести Мизеса:

(стх -^v )2 +(Су -Ф )2 +(Сх"^ )2 +--+6Р2у+ ^ + ^ )-2" ^2-=0, где: <гт - предел текучести материала; сту, т. к - компоненты тензора напряжений [1]. Тогда в случае наличия малых упругопластических деформаций элементов системы, учет физической нелинейности произведем через зависимость между вектором напряжений {а} и вектором деформаций {е}. За пределом упругости в соответствии с деформационной теорией пластичности применима формула Ильюшина А.А., которую преобразуем к символьной форме:

р} = Ю + 23 • V {с} = Ро} + 2 • G ( и ) • {8} ’ ⁽⁷⁾

где: G(и) - модуль сдвига несжимаемого за пределом упругости материала, значение которого зависит от самого деформированного состояния вследствие упрочнения ма- териала; si - интенсивность деформаций для      осесимметрической      задачи:

^ = _А^² + /3Р r- е_е⁾² + /₃Р х + Р⁾² .

В общем случае будем считать материал линейно упрочняющимся в области малых упруго-пластических деформаций. При этом истинная диаграмма o_z = Ф(б,)

может быть аппроксимирована (рис.3) зависимостью о ,.=E.8;.(1-(0),            (8)

где о - функция, учитывающая разупрочнение    материала     о = 0, при s i <  Б_т;

E-E' со =------ E

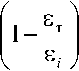
при s i < в_т, где

E '

модуль разупрочнения, который, определяют на основании диаграммы ст, = Ф(б.) для идеального линейно упрочняющегося мате- риала по известным механическим характе- ристикам (см. таблицу 1) и формуле (рис.4)

тв

^ —   /   —        ,

E (1   ) . Подставив это отношение в (7) получим

{ }   { ₀}    ² ₃ E { }    ² ₃ E { }   ...

...   { *}  2 G { } ,                        (10)

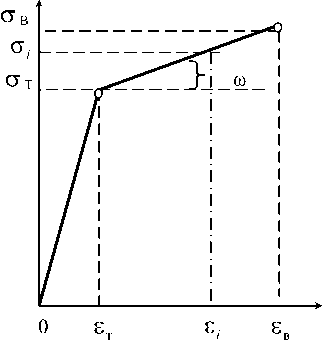
Рисунок 4 – Диаграмма линейно упрочняющегося материала где { *} вектор фиктивных упругих решений, которые возникли бы в идеальном упругом несжимаемом теле; G 1 3 E модуль сдвига, при условии несжимаемости (  =0,5).

В уравнение (6) вместо матрицы | A | c учетом физической нелинейности подставим | A |’ = | A | 2 G . При этом основное матричное уравнение (5) получим также в нелинейном виде

,            (11)

где      зависит от деформированного со стояния, являющегося однозначной функцией узловых перемещений .

Нелинейность приводит к тому, что решение системы (7) может быть получено лишь с помощью итерационных методов [2].

Для изделий, испытывающих динамические нагрузки, матричное уравнение МКЭ записывают в виде [4]: ,      (12)

где    и      общие матрица масс и век тор узловых ускорений для всей конструкции. При этом матрица    формируется с помощью известных операций по значениям ее локальных коэффициентов m , связанных с отдельным КЭ, аналогично матрице

: m            ^{( n )т    ( n )} dV , а вектор

Vn определяется в большинстве случаев ускоренным поступательным движением изделия, так что |р„| •{«„ } = X |; |р|-{#} = X , где:     плотность материала. Тогда компо ненты матрицы X определим пропорциональными ускорению изделия:

X ij       ^{p д s}         i ^{( n ) т     (} j^{n )} dV .   (13)

m

n

Таблица 1 – Механические характеристики материалов элементов

Индекс изделия, наполнения	S л н 5 &	S ■ гф С С ^ Й ( 8 i	т , МПа.	в , МПа.	т	в
3ОФ59 (корпус)	206	0,29	343	638	0,0017	0,032
3ОФ45 (корпус)	206	0,29	540	1177	0,0026	0,121
3ОФ32 (корпус)	206	0,29	334	834	0,0016	0,052
3ДС8 (корпус)	206	0,29	314	834	0,0015	0,050
3ОФ25 (корпус)	206	0,29	294	834	0,0014	0,049
3ОФ29 (корпус)	206	0,29	559	981	0,0027	0,085
3Ц30 (корпус)	206	0,29	1490	1962	0,0072	0,053
3БМ12 (сектор)	206	0,29	1200	1800	0,0020	0,045
3БМ42 (сектор)	6,98	0,27	589	700	0,0018	0,049
Наполнение (А-IX-2)	0,98	0,26	14,7	118	0,0150	0,157

Применение МКЭ наиболее эффективно при наличии полностью автоматизированной программы [2], реализующей все этапы расчета конструкции (идеализация конструкции, формирование системы уравнений (12), решение этой системы, подсчет напряжений и других величин). Программа должна быть универсальной, пригодной для широкого круга практических задач. Весьма эффективны программы, имеющие блок автоматического разбиения области на элементы, сокращающие процесс составления и контроля обширной исходной информа- ции [3 - 6].

На рис. 5,6 приведены примеры графического изображения некоторых компонент НДС конструкции, представленной конечно-элементной схемой (рис. 2). Результаты получены при p =500 МПа и р _д =300 МПа по программе [3], реализующей упругопластическую осесимметрическую задачу методом переменных жесткостей.

изделий, различающихся геометрией корпуса (цилиндрической формы - 3ОФ56; с перегородкой вблизи ВП и донной выемкой 3ОФ45, со стальным сердечником в качестве наполнения - 9СМ) и имеют различный характер. При этом наблюдается различное

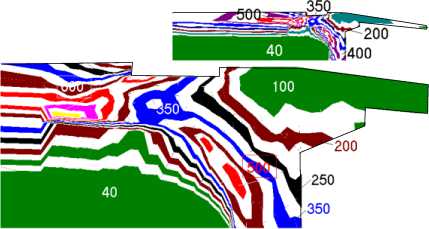
Рисунок 5 - Интенсивности напряжений, МПа (по Мизесу)

влияние сил инерции, вызываемых нагрузкой p . В одних случаях возрастание p приводит к увеличению прогиба корпуса, а в других, наоборот - к уменьшению.

В целом, вид графических зависимостей, полученных обоими способами подобен - они имеют практически линейный характер на упругом участке и криволинейный на упругопластическом (по Ильюшину - линейный), который также может быть приведен к приближенному линейному. При

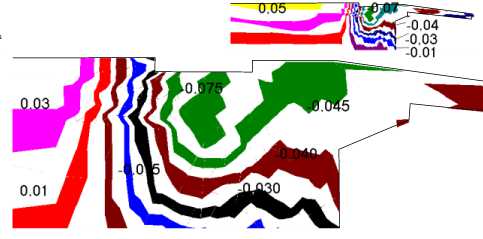
Рисунок 6 - Радиальные перемещения, мм

этом появляется возможность приведения зависимостей, полученных по МКЭ к зависимостям (2 - 4) путем введения некоторых фиктивных (“приведенных”) толщины корпуса в зоне ВП h ₀ и радиуса срединной по

верхности а ₀. Геометрические параметры "приведенной" оболочки с известным ра-

диусом наружной поверхности r можно оп-

ределить используя выражения для коэффи-

циентов A', A и B (3), определив их через

производные

A'=

а W2

и

p 0 cн

Полученные поля компонентов НДС полностью характеризуют это состояние. Их значения, в частности, можно использовать для получения зависимости радиального прогиба корпуса изделия в зоне приложения реакции p и наружного давления р _д. Пусть с учетом всех внешних сил, включая инерционные, радиальный прогиб корпуса W₂ выражается зависимостью

W₂ = W₂p + W₂p ^д - ( W₂F™ + W₂p н ),    (14)

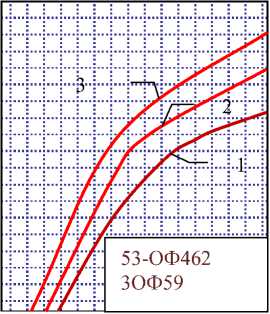
где д - радиальное давление наполнения. Тогда в результате решения задачи в рассмотренных условиях нагружения с учетом различных значений внешних сил можем получить семейство, в общем виде нелинейных, зависимостей (рис.7), которые будут характеризовать подобно зависимостям (2 -4) радиальную жесткость корпуса для заранее известной геометрии изделия. Результаты аппроксимации (рис. 7) построены для

A

W

Р сн — ⁰

соответственно на упругом

и упругопластическом участках деформирования корпуса. Для приведенных значений толщины стенки оболочки и радиуса срединной поверхности на основании построенных по МКЭ зависимостей W₂ ( р _д, p ) по-

лучим формулы:

Г • V r h0           ;

1 + ^

где обозначено:

Х = 2

h a 0 = r у

(15) ,

H

-12/3

³L A-E *(1-0.9-Х)_

.

Здесь параметры A и B могут быть переменными, если присутствует криволинейный участок. В последнем случае для каждой i -той точки кривой получим

_{B =}( A i -p i -w y

i

т

.

p , МПа 500

-0,1  0,0  0,1   0,2  0,3 W 2

p , МПа 500

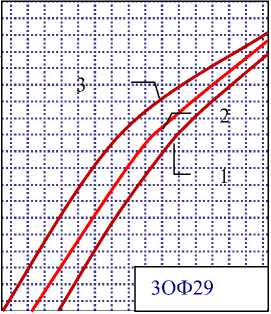
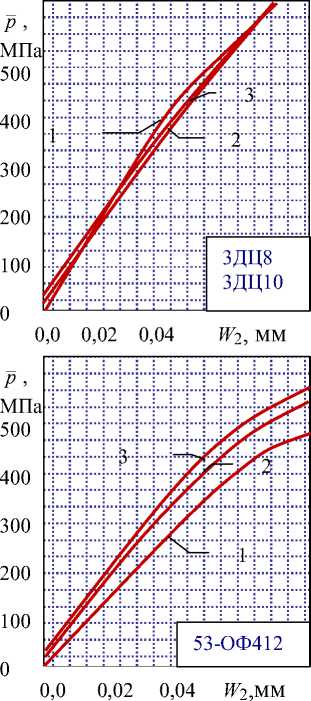
Рисунок 7 – Графики функции W ( p , p ), полученные МКЭ: 1 - р_д =0 МПа; 2 - р _д =150 МПа; 3 – p =300 МПа

-0,05 0,0  0,05  0,1 W2, мм p, МПа 500

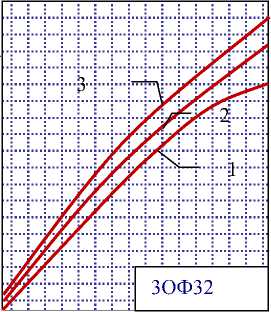
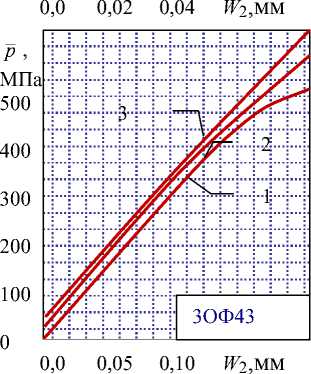
В табл. 2 приведены значения параметров h 0 и a 0 , рассчитанные по МКЭ и формулам (15) для корпусов, представленных в табл. 1. Из табл. 2. видно, что различие в расчетных значениях для традиционных схем изделия цилиндрических форм не велико (53-ОФ462,  53ОФ412,  3ОФ540,

3ОФ25, 3ОФ29, 3ОФ32), в то время как для нетрадиционных различается в несколько раз (3ОФ45, 3Ц30, 3Ц35).

Представленная система уравнений МКЭ имеет ряд условностей при применении ее для расчета НДС корпуса и других элементов изделия, испытывающих малые упругопластические деформации, обусловленные сложным нагружением в условиях функционирования. Характер нагружения элементов внешними силами (в частности корпуса) давлением и реакцией одного или двух ОК может приводить к существованию нескольких групп нагрузок, изме- няющихся независимым образом во времени и вызывающих сложное нагружение корпуса, а "эволюционный характер задачи", определяющийся развитием зон пластического нагружения, разгрузки и возможных вторичных выходов за пределы поверхности нагружения, приводит к необходимости учета "истории нагружения".

Таблица 2 – Приведенные параметры корпусов изделий (в мм)

Индекс изделия	по Ильюшину А.А.		по МКЭ
53-ОФ462 (3ОФ59)	20,71	50,37	21,5	50,2
53-ОФ540 (3ОФ25)	29,27	61,22	29,1	61,6
3ДС8	75,85	37,93	83,9	34,3
3Ц30, 3Ц34	13,64	69,03	61,4	45,5
3ОФ29	21,70	38,65	27,8	36,1
3ДЦ10	75,85	37,93	83,9	34,3
53-ОФ462 (3ОФ59)	28,07	61,47	17,1	67,7
3ОФ45	24,12	63,19	49,9	52,7
3Ц35	29,55	86,53	71,0	66,1
3ОФ43	37,57	81,72	63,2	76,8
3ОФ32	21,70	38,65	27,8	36,1
53-ОФ412	22,00	37,50	24,5	37,8

Решение упругопластической задачи с учетом истории нагружения и при наличии конечных пластических деформаций может быть получено с помощью метода последовательных приближений в совокупности с шаговой процедурой нагружения. Это значительно усложняет вычислительную процедуру МКЭ и приводит к дальнейшей дискретизации основного вариационного уравнения по i- тым шагам нагружения во времени tⁱ . Для этого вектор внешних нагрузок, переменный во времени { P } ⁱ разбивается на ряд отдельных участков { P } ⁱ , что позволяет записать уравнение (11) для i -го шага нагружения в следующем виде

K ( u ) i 1 _{A u } ⁱ   { P } ^{i 1} + { P } ⁱ ,         (17)

где { P} i   приращение вектора внешней нагрузки на участке ti 1    ti ; K(u)i1  мат рица жесткости, построенная с учетом деформированного состояния, определяемого вектором {u}i 1 на i-1-м этапе. При этом {u}i  {u}i 1 +{Au } i . С помощью этих зави симостей последовательно переходим от первого шага нагружения (i=1) ко второму

( i =2) и т.д., пока не будет получено значение вектора { u } при заданном уровне нагружения { P } . Процедура, аналогичная методу пошагового нагружения. Усложняющим отличием является наличие переменной матрицы K ( u ) .

Учитывая наличие невязки метода шагового нагружения будем производить итерационное уточнение на каждом шаге, например, методом последовательных приближений [2]. Основное матричное уравнение при этом для j -той итерации и i -го шага нагружения принимает следующий вид:

K ( u^j 1 ₎ i 1 _{A u } ^{i , j}    { P } ⁱ .             (18)

Используем данный подход для решения     задачи     о     напряженно- деформированном состоянии обтюрирующего кольца, которое вдавливается в канал трубы и испытывает конечные деформации в ее входном конусе (рис.8).

Задачу будем решать относительно нормальных ОК и касательных TК контактных напряжений на поверхности контакта ОК и трубы, которые могут быть вычислены через характеристики НДС ОК, претерпевающего пластическое формоизменения через компоненты вектора напряжений {о} у поверхности ВП по формуле cosy + ax sin• у ,    (19)

где Y – угол входного конуса относительно образующей трубы, в цилиндрической системе координат rOx (рис. 8).

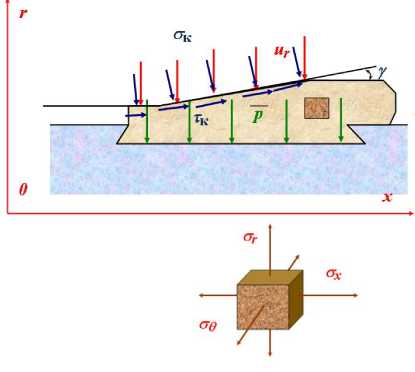
Рисунок 8 Схема деформирования ОК при вдавливании в канал трубы

В качестве граничных условий, ока- зывающих внешнее кинематическое воздействие на ОК, при решении задачи примем радиальные перемещения его поверхности ur в контактной зоне. Будем считать, что перемещение ur, определено из решения задачи более высокого иерархического уровня, учитывающей деформирование трубы Wx и корпуса W2, на котором закреплено ОК и с учетом профилей трубы R (/0 +1) и ОК r (x) вычисляется по формуле:

u_r(x ) = R ( 1 ₀ + 1-x )- r ₀ ( x )- W -W ₂ ,   (20)

где: 1 , 1₀ - путь изделия в трубе и начальное положение системы координат r0x относительно системы ROL, связанной с трубой; r ₀ ( x ) -координаты исходного профиля ОК.

Для использования вариационного уравнения (18) разобьем процесс вдавливания на ряд этапов, как этого требует теория пластического течения, и для каждого i -го этапа можем рассчитать:

A u ( x ) i = R ( 1₀ +1 - x ) - r ( x ) i ,  (21)

где r ₀ ( x ) i- текущие значения координат профиля ОК, деформируемого в процессе врезания

Г о ( x ) i = Г о ( x )^н - A U r ( x )^w + W“ (22) .

Пусть на первом этапе значения радиальных прогибов W₂ = W =0. Тогда определение граничных условий Uu_r ( x )¹ ограничивается к решению только геометрической задачи.

Для приведения задачи к квазистати-ческим условиям нагружения, необходимым для ее решения методами механики деформируемого твердого тела, на поверхности взаимодействия ОК и корпуса изделия (по поверхности канавки под ОК) S _кн введем дополнительные кинематические граничные условия - закрепления: u _r = u _x = 0, а также силовые граничные условия, соответствующие условиям трения при относительном скольжении поверхности ОК и трубы, которые пока неизвестны. Они могут быть приближенно определены по условия Зибеля по компонентам НДС, определенным из предыдущего этапа вдавливания ОК, тогда 1                   i -1

тк = а • а.  , где с.   - интенсивность на- пряжений вблизи поверхности контакта, определяемая с учетом накопленной деформации в соответствии с функциональной зависимостью Gj = Ф(е; ) на основании эксперимента для i- 1-го этапа врезания; ос - опытный коэффициент пропорциональности, предельное значение которого в зоне пластических деформаций не превышает значений ос = 1/ \/3 , а при наличии смазки (краски и др.) уменьшается в два - три раза.

К силовым граничным условиям от- несем также давление на донную часть корпуса (до ОК) pд, действующее в виде распределенной нагрузки на части свободной поверхности ОК и корпуса. Теперь задача может быть решена МКЭ - методом поша- гового нагружения с итерационным уточнением методом последовательных приближений в полном соответствии с вариационным уравнением (18)

I K ( u^Hf\b u} ^{- j} ={ P}. (23)

Результаты решения задач в виде полей компонент векторов { } и { u } приведены на рисунках 9 - 10.

Рисунок 9 - Напряженно-деформированое состояние ОК при вдавливании в канал трубы

Более полное решение может быть получено с учетом наличия деформирования корпуса W . Тогда в расчетную схему необходимо включить непосредственно сам корпус и его наполнение, а в качестве алгоритма использовать заложенный ранее для решения уравнения (23). Результат решения такой задачи приведен на рис.11.

Рисунок 10 – Деформирование ОК сложного профиля при вдавливании в канал трубы

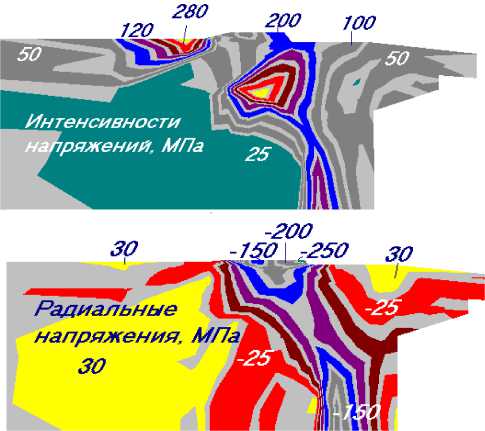
Рисунок 11 – Напряженно-деформированное состояние в зоне ОК.

Значимость этих параметров для СУ г может превышать точность учета граничных условий в области определения прогибов трубы W 1 и корпуса изделия W 2 . Значения напряжений СУ изменяются по поверхности ОК от сотен МПа до отрицательных, соответствующих "отслоению" ОК от поверхности контакта, что затрудняет расчет радиальной реакции ОК p осреднением СУ _r по поверхности контакта

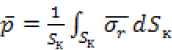
(24) с учетом формулы (19).

На рис.12 приведены распределения радиальных напряжений о в контакте ОК и трубы при вдавливании ОКП различных форм и размеров (диаметр трубы 152 мм), рассчитанные МКЭ в соответствии с изложенным алгоритмом. Из полученных графиков видно, что по мере вдавливания ОК значительно изменяется величина напряжений о и характер их распределения по контактной поверхности ОК. При этом значительную роль играет форма и размеры ОК, условия трения на поверхности контакта, угол входного конуса трубы у.

Вдавливание ОК в условиях функционирования изделия может сопровождаться рядом других процессов, оказывающих влияние на НДС ОК, которые можно учитывать через граничные условия и механические свойства его материала. В частности влияют: динамика процесса вдавливания, высокоскоростной характер трения, износ контактных поверхностей, нагревание ОК вследствие диссипации энергии трения и пластического деформирования и др.

Эти условия могут быть учтены путем поднятия иерархического класса математической модели за счет включения в нее перечисленных процессов, что усложняет саму задачу и ее параметрическую идентификацию.

Указанные недостатки присущи всем известным решениям НДС элементов изделий численными методами. Тем не менее, такое решение может быть использовано для расчетной оценки возможности применения различных материалов с учетом конструкций ОК по критериям, связанным с пластическими свойствами материалов, претерпевающих конечные пластические деформации, например по наибольшими допустимым деформациям [ г ], приводящим к разрушению ОК при вдавливании, т.е. по условию 8 [8], где 8 наибольшее значение компоненты вектора { г }. Решая последовательно ряд задач с изменением кинематических граничных условий u (0.

u ), возможно установление параметрической зависимости вида p = f ( u_r ).

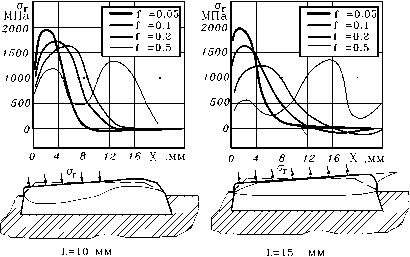
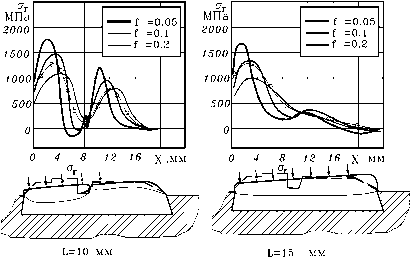
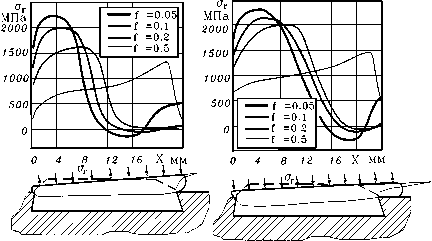
L=20 мм

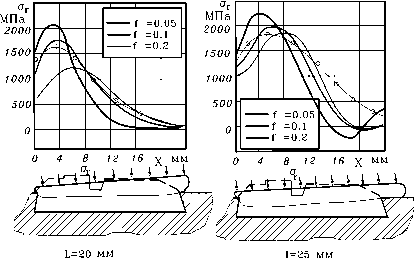
Рисунок 12 - Распределение радиальных напряжений по поверхности ОК различных профилей

Такая зависимость позволит аппроксимировать задачу расчета НДС при вдавливании ОК для следующих иерархических уровней путем построения "кривых вдавливания", которые совместно с зависимостями (2 - 4, 14) позволит решить задачу вдавливания ОК на более высоком иерархическом уровне.

Алгоритм расчета радиальных и осевых взаимодействий изделия и трубы будем строить на основании функциональных связей между радиальными прогибами трубы Wx и корпуса изделия W2 с радиальной реакцией ОК p, полученными на основании численных решений задач МКЭ в виде табличных (графических) зависимостей для прогибов W2 (p, рд) (рис.7), считая, что давление pд известно. Причем учитывая общую постановку задачи о НДС численным методом (МКЭ) можем получить зависимость W2 (p, рд, x), где x - координата поверхности ОК. Предположим, что эта зависимость может быть выражена полиномом второго порядка по степеням x , тогда имеем:

^W 2 ⁽ p , p д , x ) = ^W 2 x =0 ⁽ p , p д) + -

2 ,   (25)

... + c1( p, p д )' x + c 2( p, p д )" x где W2x=o(p, pд) “ зависимость W,(p, pд) построенная для точки поверхности ОК с координатой x =0 мм (расположенной у верхней кромки ОК) (рис. 13); c1(p, pд), c2(p, pд) - коэффициенты полинома, зави- сящие в общем случае от условий нагруже-

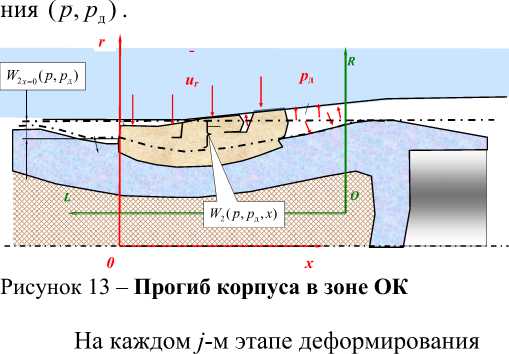
ОК в процессе вдавливания и после него, для каждой точки поверхности ОК с координатой x i граничные условия в перемещениях u_r ( x ) определяются из решения трех следующих задач:

• 1.    Деформирования трубы реакцией ОК p и давлением p _д

  W W ^p W ^{p д} ,

  
  

  где

  
  

• 2.    Деформирования корпуса изделия реакцией ОК p и давлением в канале p _д;

• 3.    Деформирования материала ОК в

W1p = k тр ■ p; W1pд = k т^р • Рд , где k т^р и kтр- коэффициенты жесткости трубы определяется из решения задачи радиального деформирования трубы (как правило упругой) кольцевыми нагрузками p д и p,соответственно, например с использованием МКЭ [3];

условиях заданного значения давления p _д и известных граничных условиях (21).

Решение перечисленных, взаимосвязанных граничными условиями, задач может производится методом простых итераций. Причем решение первых двух задач представляется табличными зависимостями W2x=о(p,pд), ci(p,pд), c2(p,pд), построенными численно по МКЭ, а третья задача решается по МКЭ в уравнениях (23) с учетом (24), устанавливающих связь между внешними силовыми p и кинематическими u.(x) параметрами. Графическая интерпретация алгоритма приведена на рис. 14. При этом за начало итераций приняты условия, в которых прогибы трубы и корпуса изделия определены на предыдущем j-1 -м этапе деформирования u,0=(R-r)j-W.j-I-W,jV (26)

Условие (26) безразлично для организации итераций, но позволяет максималь- но сократить их число или вовсе их исклю- чить при достаточно малом этапе деформи-

W 2^ p j -1 , p д j _1 , x ) ^в

рования, принимая

начале этапа решения третьей задачи и вы- числяя W2

( pj , p д j’

x

в конце этапа.

Условием выхода из итераций, явля- ется следующее:

W,+w:,)i-W,+w„)„1 (Wj + W2,X орга-

низованное по i-тым итерациям, где s-любая наперед заданная приемлемая погрешность

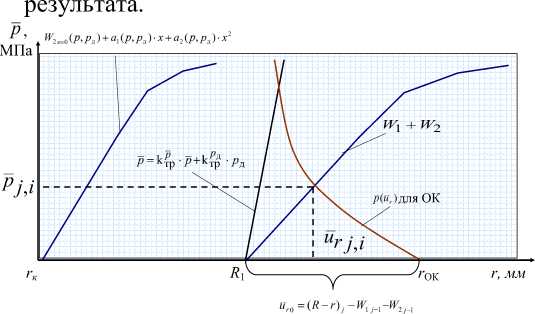
Рисунок 14 - Геометрическая интерпретация алгоритма расчета реакции ОК

На практике необходимо учитывать то, что, в общем случае, профиль канала трубы может быть сложным вследствие неравномерного по его длине радиального износа, возникающего в процессе работы системы, тогда профиль канала трубы выразим табличной функцией R ( L ), причем в процессе движения будет изнашиваться и поверхность самого ОК - А г изн . Еще одним фактором, требующим учета, является переменная во времени (в процессе движения изделия по трубе) величина давления в канале, тогда - p _д (1 ) . Действие перечисленных факторов в процессе движения изделия по каналу трубы может приводить к разгрузке ОК. При этом реакция ОК p будет определяться условиями упругих взаимодействий системы "труба - ОК - корпус изделия". Причем возможно появление зазора между поверхностями ОК и трубы. Схема разгрузки ОК приведена на рис. 15. На участке разгрузки кривая p ( u_r ) сохраняет наклон вследствие упругих свойств ОК (рис.15), которые можно учитывать зависимостью

Р(x) = Р(x) j-1 -E -utr (x) j-1 - ur (x) j ) h(x) , где p(x)max - наибольшее значение реакции ОК (радиальных напряжений) в точке контакта на предыдущем этапе. E - модуль уп- ругости материала ОК; h(x) - высота профиля ОК относительно координаты рассматриваемой точки поверхности.

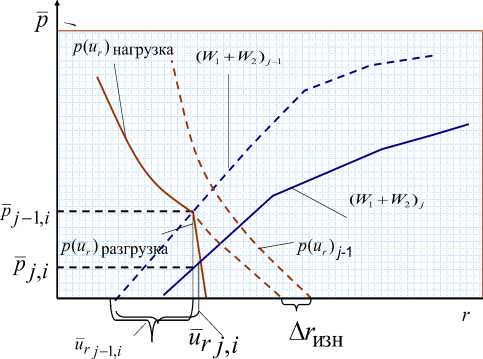
Рисунок 15 - Геометрическая интерпретация алгоритма расчета реакции ОК на этапе разгрузки

Условием появления зазора и его величиной в рассматриваемой точке поверхности ОК с координатой xi будет рассчитанное в результате итераций отрицательное значение ur(xi) = [R(L-xi)-r(xi)]j -...

... -W i (L-X i)- W ₂ (x ^cO. (27)

Алгоритм расчета радиальных и осевых взаимодействий можно представить схемой, реализованной в ПК INNER [6], изображенной на рис. 16.

Установленная алгоритмом (рис. 16) зависимость между внешними силовыми p и кинематическими u ^x) параметрами, связанными с геометрией трубы и элементов изделия, с учетом их радиальных прогибов, позволяет в полной мере учитывать конструктивные особенности всех элементов рассматриваемой системы, а также нестабильности, связанные с технологией их изготовления и условиями процесса, в частности, с изнашиванием поверхности канала трубы и др.. В расчете характеристик силового взаимодействия можно учитывать множество других значимых факторов, изменяющихся в условиях функционирования изделия (pд, коэффициента трения f тр, скорости изделия v и др.) [6].

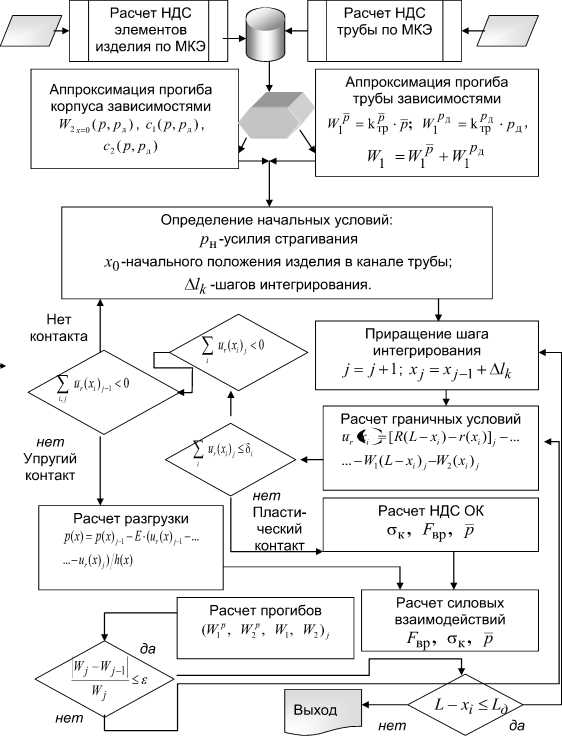
Рисунок 16 - Алгоритм расчета радиальных и осевых взаимодействий

При износе канала трубы в процессе работы системы происходят необратимые изменения геометрии канала, которые влекут за собой значительные изменения условий силового взаимодействия. В частности, с износом увеличивается время и путь процесса вдавливания, его динамичность и сложность условий силового взаимодействия, обусловленные неравномерным износом поверхности канала.

В табл. 3 и на рис. 17. приведены ре- зультаты сопоставительных расчетов, реализованные в ПК INNER характеристик силового взаимодействия для 152 мм изделия с обтюрирующим кольцом сложного гео- метрического профиля и труб, имеющих продольные нарезы и различный износ, в соответствии с числом реализаций процесса N = 0, 412, 900.

Из таблицы видно, что с числом реализаций процесса интенсивность радиальных реакций растет, а осевых составляющих силового взаимодействия снижается (рис. 17). Последнее обусловлено значительным снижением коэффициента трения f _тр , изменение величины которого учитывалось по специальному алгоритму [7]. Пример графического изображения этих характеристик приведен на рисунке 17.

Таблица 3 – Наибольшие значения характеристик силового взаимодействия

Характеристика силового взаимодействия	Число реализаций процесса N
	0	412	1000
Сила сопротивления движению Fвр ,max , КН	587	271	257
Путь до Fвр ,max , мм	107	1133	1216
Радиальная реакция p max , МПа	146	203	214
Путь до p max , мм	113	1133	1216
Контактное давление под полем о к 1 ,max , МПа	443	466	488
Контактное давление под нарезом о к 2 ,max , МПа	312	231	171
Радиальный прогиб тру бы W 1 ,max , мм	0,178	0,218	0,209
Радиальный прогиб корпуса W 2 ,max , мм	0,038	0,0195	0,0318

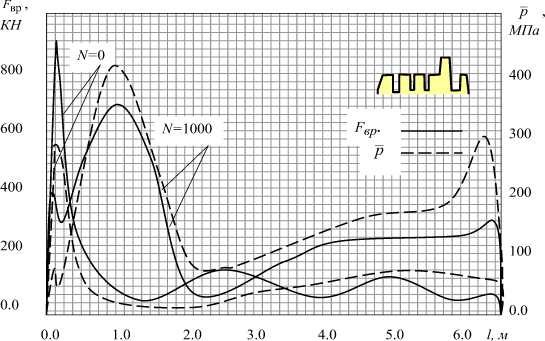
Рисунок 17 – Характеристики силового взаимодействия в новой и изношенной трубах