Удвоитель сверхвысокой частоты на квадратурных мостах и балансных преобразователях

Умножители сверхвысокой частоты (СВЧ) находят широкое применение в устройствах радиолокации, генерации сигналов [5], устройствах оперативного измерения частоты [3], сфере телекоммуникаций и др. Наибольшей полосой рабочих частот при приемлемом уровне подавления паразитных гармоник обладают балансные удвоители частоты [2]. Подавление нечетных гармоник в балансных умножителях частоты достигается за счет противофазной работы двух полупроводниковых приборов (транзисторов или диодов) [15]. При этом рабочая точка транзисторов для максимизации уровня второй гармоники выбирается вблизи области отсечки, что делает входное и выходное сопротивления транзисторов преобладающе комплексным [6]. Это затрудняет согласование удвоителя по входу и выходу и, таким образом, увеличивает коэффициенты отражения по входу и выходу. Высокие коэффициенты отражения по входу и выходу могут приводить к возбуждению и генерации нежелательных колебаний, высоким неравномерностям амплитудно-частотных характеристик (АЧХ) тракта, нежелательному изменению частоты генераторов СВЧ. В литературе по теме не удалось обнаружить четких требований к входному и выходному коэффициентам отражения для удвоителей частоты. Однако для существующих широкополосных удвоителей частоты, выполненных в виде монолитной интегральной схемы (МИС), максимальное значение модуля коэффициента отражения как по входу [7, 10, 11], так и по выходу [11, 13] принимает значения –10…–5 дБ. Примем это значение как верхнюю границу для модуля входного и выходного коэффициентов отражения. Вместе с тем к удвоителям частоты предъявляются следующие требования [4]:

• 10 м оделирование технических устройств

• 1)    максимальная широкополосность;

• 2)    выходная мощность порядка единиц мВт;

• 3)    равномерность выходной мощности ± 1,5…2 дБ;

• 4)    подавление побочных гармонических составляющих в спектре выходного сигнала не менее 20…25 дБ;

• 5)    пороговая мощность по входу не более 30…100 мВт.

В связи с этим представляет интерес схема удвоителя частоты СВЧ с улучшенным согласованием по входу и выходу, удовлетворяющая указанным требованиям.

Постановка задачи и способы решения

Известен способ согласования мощных транзисторов, входное и выходное сопротивления которых сильно отличаются от волнового сопротивления линии передачи [14]. Способ заключается в балансном включении двух идентичных усилителей через квадратурные мосты или четвертьволновые линии передачи на входе и выходе. Отраженные от входа и выхода усилителей (транзисторов) волны, проходя через квадратурные мосты, выделяются на входе и выходе квадратурных мостов в противофазе и взаимно компенсируются. Другая часть отраженных волн выделяется в фазе на изолированных портах квадратурных мостов и поглощается в согласованной нагрузке. Так как умножение частоты увеличивает также фазовый набег, приобретаемый во входном квадратурном мосте, указанный способ нельзя непосредственно перенести на случай умножителя частоты. Нарушение баланса фазы из-за умножения фазового набега приведет к снижению степени подавления нежелательных гармоник на выходе удвоителя частоты. Тем не менее для применения указанного способа входные и выходные цепи удвоителя должны содержать квадратурные мосты. Следовательно, необходимо разработать схему удвоителя частоты с квадратурными мостами на входе и выходе, одновременно обеспечивающую согласование по входу/выходу и сохранение фазовых соотношений между гармониками на выходе умножителя частоты.

Известно, что степень подавления паразитных гармоник в балансных удвоителях частоты зависит от баланса амплитуд и фаз входного балансного преобразователя, а также разброса параметров активных приборов [12]. В связи с этим для рассматриваемого удвоителя частоты необходимо рассмотреть зависимость степени подавления паразитных гармоник и входного/выходного коэффициентов отражения от следующих факторов: баланса фазы и амплитуды пассивных устройств, разброса параметров активных приборов. Для упрощения анализа ограничимся третьей гармоникой входного сигнала. Для анализа работы удвоителя частоты применим нелинейные параметры рассеяния в режиме большого сигнала [9], так как они позволяют получить выражения для выходных гармоник входного сигнала с учетом фазового набега, приобретаемого вследствие умножения частоты. Кроме того, нелинейные параметры рассеяния позволяют рассмотреть коэффициенты отражения по входу/выходу на частоте основного сигнала и на его гармониках.

Математическая модель удвоителя частоты

Рассмотрим схему бинарного деления/суммирования мощности, представленную на рисунке 1. Схема состоит из квадратурных мостов 1 , 10 ; балансных преобразователей 2 , 3 ; активных элементов 4 , 5 , 6 , 7 ; синфазных сумматоров мощности СВЧ 8 , 9 . Заглавными и прописными буквами на схеме указаны порты устройств. Абстрагируемся от фазовых

Удвоитель сверхвысокой частоты на квадратурных мостах...

сдвигов, указанных на рисунке 1, и предположим, что устройства 1 , 2 , 3 сдвигают фазу выходных волн относительно входных волн на углы (φ₁, φ₂), (φ₃, φ₄), (φ₅, φ₆). Устройства 8 , 9 , 10 суммируют входные волны, предварительно сдвигая их фазы на углы (φ₇, φ₈), (φ₉, φ₁₀), (φ₁₁, φ₁₂).

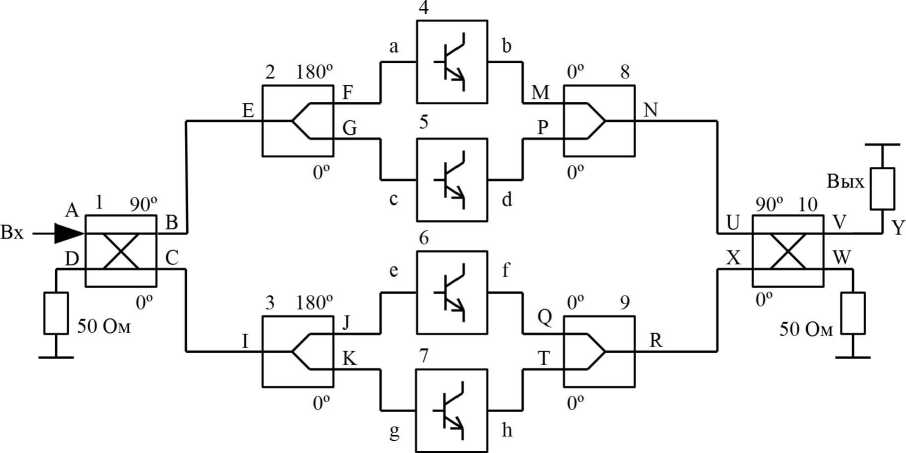
Рис. 1. Схема удвоителя частоты на квадратурных мостах и балансных преобразователях

Запишем выражения для гармоник S ₁, S ₂, S ₃, входного сигнала на выходе устройства (на выходе элемента 10 ). Для упрощения примем, что делители/сумматоры и активные элементы имеют идентичные параметры. В итоге для выходного сигнала на первой, второй и третьей гармониках для момента времени t = 0 получим нормированную относительно амплитуды входного сигнала и коэффициентов передачи систему уравнений:

S ₁ = cos(φ₀ + φ₁ + φ₃ + φ₇ + φ₁₁) + cos(φ₀ + φ₁ + φ₄ + φ₈ + φ₁₁)+ +cos(φ₀ + φ₂ + φ₅ + φ₉ + φ₁₂) + cos(φ₀ + φ₂ + φ₆ + φ₁₀ + φ₁₂) , S ₂ = cos(2(φ₀ + φ₁ + φ₃)+φ₇ +φ₁₁) + cos(2(φ₀ + φ₁ + φ₄) + φ₈ + φ₁₁)+ +cos (2(φ₀ + φ₂ +φ₅) +φ₉ +φ₁₂) + cos(2(φ₀ + φ₂ + φ₆) + φ₁₀ + φ₁₂), S ₃ =cos(3(φ₀ + φ₁ +φ₃) + φ₇ + φ₁₁)+ cos(3(φ₀ + φ₁ + φ₄)+ φ₈ + φ₁₁)+ +cos(3(φ₀ + φ₂ + φ₅) + φ₉ +φ₁₂)+ cos(3(φ₀ + φ₂ + φ₆)+ φ₁₀ + φ₁₂) ,

где φ₀ – начальная фаза сигнала; S ₁– сигнал на выходе бинарной схемы (рис. 1) на первой гармонике; S ₂ – сигнал на выходе бинарной схемы на второй гармонике; S ₃ – сигнал на выходе бинарной схемы на третьей гармонике.

Так как система (1) состоит из трех уравнений, а неизвестных переменных 12, она не может быть решена известными способами. Для поиска ее решения была применена процедура перебора углов φi с шагом π/2, где i = 1…12, со следующими ограничениями:

• 1)    вносимый устройствами 1 – 3 , 8 – 10 фазовый сдвиг при передаче с входа на любой из выходов (и наоборот) должен принимать значения 0, π/2 или π;

• 2)    вносимый устройствами 1 – 3 , 8 – 10 фазовый сдвиг при передаче с входа на выход (и наоборот) не должен одновременно для обоих выходов принимать значение π/2 или π;

12 м оделирование технических устройств

• 3)    сумма фазовых сдвигов при передаче с входа на первый и второй выходы для каждого из устройств 1 – 3 , 8 – 10 должна быть меньше 3π/2.

Ограничение 1 направлено на реализацию элементов 1 – 3 , 8 – 10 с помощью известных синфазных делителей/сумматоров, квадратурных ответвителей (мостов) и балансных преобразователей.

Ограничение 2 направлено на исключение ситуации, когда фазовый сдвиг коэффициентов передачи с входа на первый и второй выходы каждого из элементов 1 – 3 , 8 – 10 имеет одинаковое значение.

Ограничение 3 направлено на исключение ситуации, когда фазовый сдвиг одного из коэффициентов передачи с входа на выход элементов 1 – 3 , 8 – 10 имеет значение π/2, а фазовый сдвиг другого коэффициента передачи с входа на выход имеет значение π.

В результате процедуры перебора с указанными условиями были найдены следующие значения углов: φ1= 90, φ2= 0, φ3 = 180, φ4 = 0, φ5 = 180, φ6 = 0, φ7 = 0, φ8 = 0, φ9 = 0, φ10= 0, φ11 = 90, φ12 = 0. С учетом этого схема удвоителя частоты примет вид, представленный на рисунке 1.

Запишем выражение для комплексного входного коэффициента отражения S ^e _{AA 11} удвоителя частоты, рассмотрев последовательность многократно отраженных от неоднородностей волн [1]. Падающая на вход ответвителя 1 от генератора волна с комплексной амплитудой а_{А 1} частично отразится, частично пройдет на вход балансных преобразователей 2 и 3 . Комплексная амплитуда частично отраженной от входа ответвителя 1 волны пропорциональна а_{А 1} S_{AA 11}, где S_{AA 11} – комплексный входной коэффициент ответвителя 1 . Комплексная амплитуда частично отраженных от входа балансных преобразователей 2 и 3 волн, прошедших на порт A ответвителя 1 , пропорциональна а_{А 1} S_{BA 11} S_{EE 11} S_{AB 11} и а_{А 1} S_{CA 11} S_{II 11} S_{AC 11} соответственно, где S_{BA 11}, S_{AB 11}, S_{CA 11}, S_{AC 11} – комплексные коэффициенты передачи ответвителя 1 с порта A на порты B , C и обратно. Коэффициенты S_{EE 11} и S_{II 11} – входные комплексные коэффициенты отражения балансных преобразователей 2 и 3 . Продолжая по аналогии, учитывая только однократно отраженные волны и считая активные устройства 4 – 7 однонаправленными, суммируя частично отраженные волны, выполняя деление полученной суммы отраженных волн на а_{А 1}, запишем выражения для входного коэффициента отражения удвоителя частоты при условии, что комплексные коэффициенты передачи S_{BC 11}, S_{CB 11}, S_{FG 11}, S_{GF 11}, S_{JK 11}, S_{KJ 11}<< 1:

S AA 11 ≈ S AA 11 + S BA 11 S EE 11 S AB 11 + S CA 11 S II11 S AC 11 +

+ SBA11SFE11Saa11SEF11SAB11 + SBA11SGE11Scc11SEG11SAB11 + (2) + SCA11SJI11See11SIJ11SAC11 + SCA11SKI11Sgg11SIK11SAC11, где SΨΩ11 – линейный комплексный коэффициент передачи (параметр рассеяния) с порта Ω на порт Ψ (заглавные буквы на рис. 1) на первой гармонике; SΩΩ11 – линейный комплексный коэффициент отражения (параметр рассеяния) от порта Ω (заглавные буквы на рис. 1) на первой гармонике; Sββ11 – нелинейный комплексный коэффициент отражения (параметр рассеяния) от порта β (прописные буквы на рис. 1) на первой гармонике.

у двоитель сверхвысокой частоты на квадратурных мостах...    13

Введем в выражение (2) фазовые соотношения, указанные на рисунке 1. Пусть квадратурный мост 1 и балансные преобразователи 2 , 3 имеют фазовые неидентичности δ₁, δ₂, δ₃ (то есть φ₁= 90 + δ₁; φ₃= 180 + δ₂; φ₅= 180 + δ₃) в диапазоне рабочих частот. Тогда входной коэффициент отражения на первой гармонике примет вид

S^e_{AA 11} ≈ S_{AA 11} + S_{EE 11}| S_{BA 11} S_{AB 11}| e^{– j π–2 j δ1} + S_{II 11}| S_{CA 11} S_{AC 11}|+

• ^{+    S}aa 11 ^{| S}BA 11 ^SAB 11 ^SFE 11 ^SEF 11 ^{| e –3 j π–2 j δ1–2 j δ2 + S}cc 11 ^{| S}BA 11 ^SAB 11 ^SGE 11 ^SEG 11 ^{| e – j π–2 j δ1 +}           (3)

• ^{+    S}ee 11 ^{| S}CA 11 ^SAC 11 ^SJI 11 ^SJI 11 ^{| e –2 j π–2 j δ3 + S}gg 11 ^{| S}CA 11 ^S AC 11 ^SKI 11 ^S IK 11 ^|,

где j – мнимая единица.

Раскладывая экспоненту в выражении (3) в ряд Тейлора, ограничиваясь первыми двумя членами ряда, и группируя слагаемые, получим выражение для входного коэффициента отражения на первой гармонике при малых углах фазовой неидентичности квадратурного моста 1 и балансных преобразователей 2 и 3 :

• ^S AA 11 = S AA 11 ^{[ S}II 11 I ^SCA 11 ^S AC 11 I — ^SEE 11 1 ^S,A 11 ^SA, 11K ¹ — ²A^{)] +}

+ [ S_{ee 11}| S_{CA 11} S_{AC 11} S_{JI 11} S_{IJ 11}|(1 – 2 j δ₃) – S_{aa 11}| S_{BA 11} S_{AB 11} S_{FE 11} S_{EF 11}|(1 – 2 j δ₁– 2 j δ₂) ] + ₍₄₎

+ [ ^Sgg 11 1 S CA 11 S AC 11 ^SK, 11 ^S|K 11 1 — S . 11 | S ,A „ S ,. „ ^Sge „ ^Seg J(1 — 2j $ 1 ) ] ,

Воспользуемся описанной выше методикой для записи выражений для выходных коэффициентов отражения S ^e _VVii ( i = 1…3, где i указывает номер гармоники) при фазовых неидентичностях δ₄, δ₅, δ₆ элементов 8 – 10 (то есть φ₇= δ₄, φ₉= δ₅, φ₁₁ = 90 + δ₆). Выходной коэффициент отражения S ^e _VVii удвоителя частоты при малых фазовых неидентичностях элементов 8 – 10 на первой, второй и третьей гармониках при условии, что коэффициенты передачи элементов 8 – 10 S_{MP 11}, S_{PM 11}, S_{QT 11}, S_{TQ 11}, S_{UX 11}, S_{MP 22}, S_{PM 22}, S_{QT 22}, S_{TQ 22}, S_{UX 22}, S_{MP 33}, S_{PM 33}, S_{QT 33}, S_{TQ 33}, S_{UX 33}<< 1, учитывая только однократно отраженные волны, можно представить в виде

• ^S ™ = S VV. + ^[ S J ^S„, i^S™i l — S NNii I ^S„> A ™ K¹ — ² j $ б )] +

+ [ S_ffii | S_XViiS_VXiiS_QRiiS_RQii |(1 – 2 j δ₅) – S_bbii | S_UViiS_VUiiS_MNiiS_NMii (1 – 2 j δ₆– 2 j δ₄) ] +    (5)

• +    ^[ S hii I S v ^S>Xi S TR,^S,T. | - ^Sdd. | ^SUVii ^SVUi S pN,^SNp^i |⁽¹ - ² j $ 6 ) ] ,

где i = 1…3.

Для установления связи между уровнем полезного сигнала, а также уровнем паразитных гармоник с параметрами элементов удвоителя частоты необходимо выразить комплексные амплитуды отраженных волн b_{V 1}, b_{V 2}, b_{V 3}на выходе ответвителя 10 через комплексную амплитуду падающей на вход ответвителя 1 волны a_{A 1}. Для этого применим методику, описанную в [8], совместно с методикой, примененной ранее для нахождения входного коэффициента отражения. С учетом этого комплексную амплитуду отраженной волны b_Vi ( i = 1…3, где i указывает номер гармоники) на выходе умножителя частоты при условии Г_S = 0, где Г_S – коэффициент отражения источника сигнала, можно представить в следующем виде:

Моделирование технических устройств bVi =

a A 1 S BA 11 S FE 11 S bai 1 S NMii S VU ii

’--------"c-----+

¹BB 11 S EE 11 )

^{( 1 S}VVii^SYYii )^{( 1} S FF 11 ^Saa 11 ) ( 1 ^Sbbii^SMMii )( 1    ^SNNii^SUUii )( 1    ^S j

+

^{(1 - S}vv„^Syy,, ^{)(1 - S}

a A 1 ^SBA 11 ^SGE 11 ^Sdci1 ^SNPii^SVUii

+

^{(1 -} S VVii S YYii ⁾⁽¹ — S

'BB 11 SEE 11)(1   SGG 11 Scc11)(1   SddiiSPPii )(1   SNNiiSUUii a A1SCA11SJI11 Sfei 1 SRQiiSVXii

+

'CC 11SII 11)(1   SJJ11 See11)(1   SffiiSQQii )(1   SRRiiSXXii aA1SCA11SKI11Shgi1SRTiiSVXii

+

KK 11 S gg 11

'RRii S Xxii )( 1 - S VV 11 S YYii ) '

где a_{A 1} – комплексная амплитуда падающей на порт А волны на первой гармонике от источника сигнала;

S^e  ≈ S + S S S + S S S ;

EEii EEii FEii aaii EFii GEii ccii EGii

S^e ≈ S + S S S + S S S ;

IIii IIii JIii eeii IJii KIii ggii IKii ^e

MMii MMii NMii UUii MNii NMii VUii YYii UVii MNii ;

^e S PPii

S

S

S

e QQii e TTii e UUii

≈ S PPii + S NPii S UUii S PNii + S NPii S VUii S YYii S UVii S PNii ;

i ≈ S QQii + S RQii S XXii S QRii + S RQii S VXii S YYii S XVii S QRii ;

≈ S TTii + S RTii S XXii S TRii + S RTii S VXii S YYii S XVii S TRii ;

^e S XXii

≈ S_UUii + S_VUiiS_YYiiS_UVii ;

≈ S XXii + S VXii S YYii S XVii ;

i = 1...3.

Введем в выражение (6) фазовые неидентичности δ₁, δ₂, δ₃, δ₄, δ₅, δ₆элементов 1 , 2 , 3 , 8 , 9 , 10 . При этом учтем, что умножение частоты приводит также к умножению начальной фазы сигнала. Проводя те же операции, что и при выводе выражений (4), (5), получим выражения для отраженных волн на выходе квадратурного сумматора мощности СВЧ 10 на первой, второй и третьей гармониках при малых углах фазовой неидентичности элементов 1 – 3 , 8 – 10 :

b V 1

______________ ^aA 1 | ^SBA 11 ^SfE 11 ^SNM 11 S VU 11 | ^Sba 11 ^{( 1} j ^ 1 j ^ 2 j ^ 4 j ^ 6 ) _____________ ^{( 1} - S VV 11 ^SYY 11 ^{)( 1} - ^SBB 11 S EE 11 ^{)( 1} - ^STT 11 ^Saa 11 ^{)( 1} - ^Sbb 11 ^SMM 11 ^{)( 1} - ^SNN 11 ^SUU 11

-

a A 1 S BA 11 S

'GE 11 ^SNP 11 ^SVU 11 | ^Sdc 11 ^{( 1} j ^ 1 j ^ 6 )

^{( 1} S VV 11 S il 11 ^{)( 1} S BB 11 S EE 11 ^{)( 1} S GG 11 S cc 11 ^{)( 1 S}dd 11 ^SPP 11 ^{)( 1 S}NN 11 ^SUU 11 )

-

a A 1 S CA 11 S JI 11 S

'RQ 11 ^SVX 11 | ^S/e 11 ^{( 1} j ^ 3    j ^ 5 )

^{( 1}   S VV 11 S TY 11 ^{)( 1 S}CC 11 ^SII 11 ^{)( 1   S}JJ 11 S ee 11 ^{)( 1   S}ff 11 ^S QQ 11 ^{)( 1   S}T M1 S XX 11

+

^{( 1} — ^SVV 11 S ir 11 ^{)( 1} — S

aA1 SCA11SKI11SRT11SVX11 S hg11

Удвоитель сверхвысокой частоты на квадратурных мостах...

b_{V 2}

ja A 1 S BA 11 S FE 11 S ba 21 S NM 22 S VU 22 (1-2 jδ 1 -2 jδ 2 - jδ 4 - jδ 6 )

(1-SVV22SYY22 )(1-SBB11SeEE11)(1-SFF11Saa11)(1-Sbb22SeMM22)(1 - SNN22SeUU22)

-

ja A 1 S BA 11 S GE 11 S dc 21 S NP 22 S VU 22 (1-2 jδ 1 - jδ 6 )                    +

(1-SVV22SYY22 )(1-SBB11SeEE11)(1-SGG11Scc11 )(1 - Sdd22 SePP22 )(1 - SNN22 SeUU22 )

a A 1 S CA 11 S JI 11 S fe 21 S RQ 22 S VX 22 (1-2 jδ 3 - jδ 5 )

(1-SVV22SYY22 )(1 - SCC11 SIeI11 )(1-SJJ11See11)(1

-

S ff 2 2 S ^e QQ 22 )(1 - S RR 22

+

(1 - S_{VV 22}

a A 1 S CA 11 S KI 11 S hg 21 S RT 22 S VX 22

S YY 22 )(1- S CC 11 S I ^e I 11 )(1- S KK 11 S gg 11 )(1- S hh 22 S TT ^e 2 2 ) ( 1 - S RR 22 S X ^e X 22 )

b V 3

a A 1 ^S BA 11 S _FE 11 S ba 31 S NM 33 ^Svu 33 ( 1 ^{3 j} 8 1   ³ j 2    ^4    jS 6 )

^{( 1 S}VV 33 S yy 33 ^{)( 1 S}BB 11 S EE 11 ^{)( 1 S}FF 11 ^Saa 11 ^{)( 1 S}bb 33 ^SMM 33 ^{)( 1 S}NN 33 ^SUU a A 1 ^SBA 11 ^SGE 11 ^Sdc 31 ^SNP 33 ^SVU 33 ^{( 1} - ^{3 jS} 1 - ^jS 6 )

^{( 1} S VV 33 S yy 33 X¹ S BB 11 S EE 11 ^{)( 1 S}GG 11 ^Scc 11 ^{)( 1 S}dd 33 ^SPP 33 X^{1 S}NN 33 ^SUU 3з ) a A 1 ^SCA 11 ^SJI 11 ^S fe 31 ^SRQ 33 ^SVX 33 ^{( 1} - ³ j ^S 3 - ^jS 5 )

( 1 - S VV 33 S yy 33 ^{)( 1} - S CC 11 ^SII 11 ^{)( 1} - S JJ 11 S ee 11 ^{)( 1} - ^Sff 33 ^SQQ 33 ^{)( 1} - ^SRR 33 ^SXX 33 )

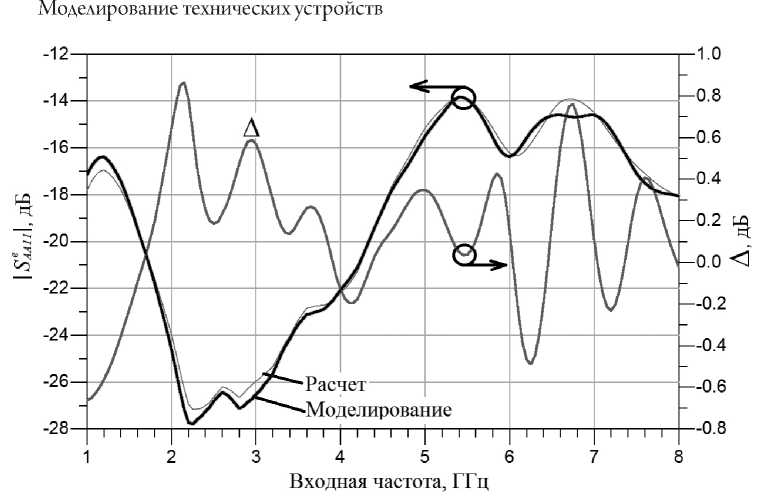
Рис. 2. Модуль входного коэффициента отражения умножителя частоты на первой гармонике

График на рисунке 2 показывает, что представленная схема удвоителя частоты обеспечивает значение модуля входного коэффициента отражения, не превышающее –20 дБ в диапазоне частот 2…4 ГГц и не превышающее –12 дБ в диапазоне частот 1…8 ГГц. Данная схема удвоителя по указанному параметру превосходит представленные в [7, 10, 11] схемы умножителей частоты и удовлетворяет требованиям, указанным во введении.

I Sm/I, дБ

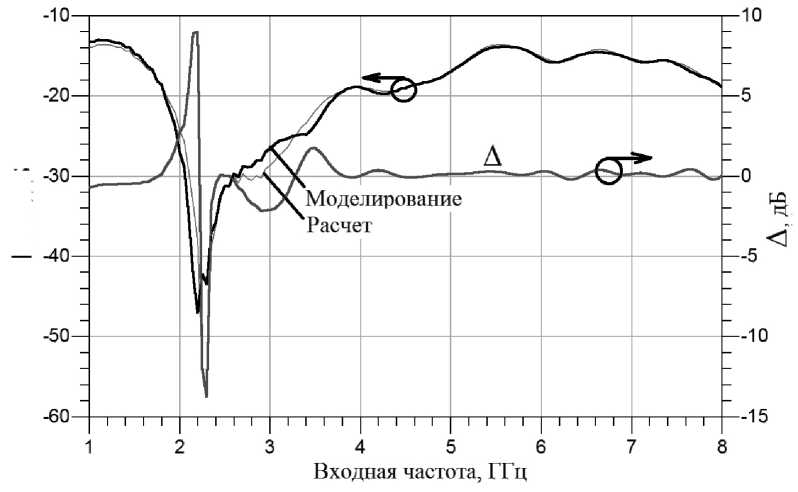
Рис. 3. Модуль выходного коэффициента отражения умножителя частоты на первой гармонике

Удвоитель сверхвысокой частоты на квадратурных мостах...

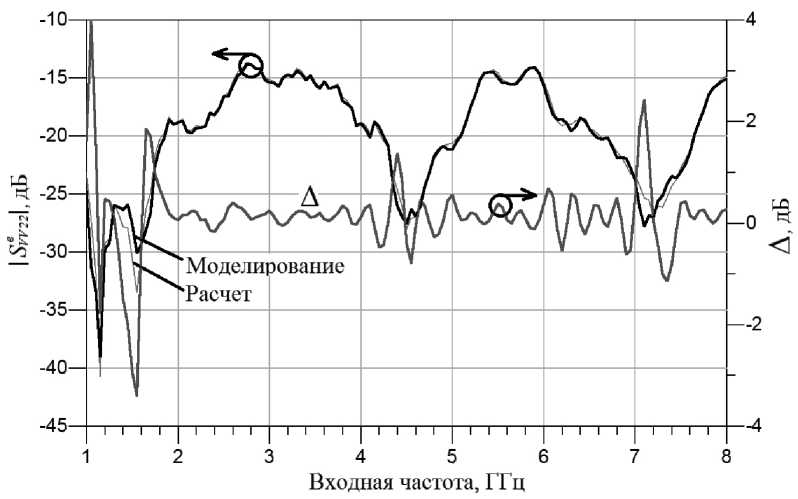
Рис. 4. Модуль выходного коэффициента отражения умножителя частоты на второй гармонике

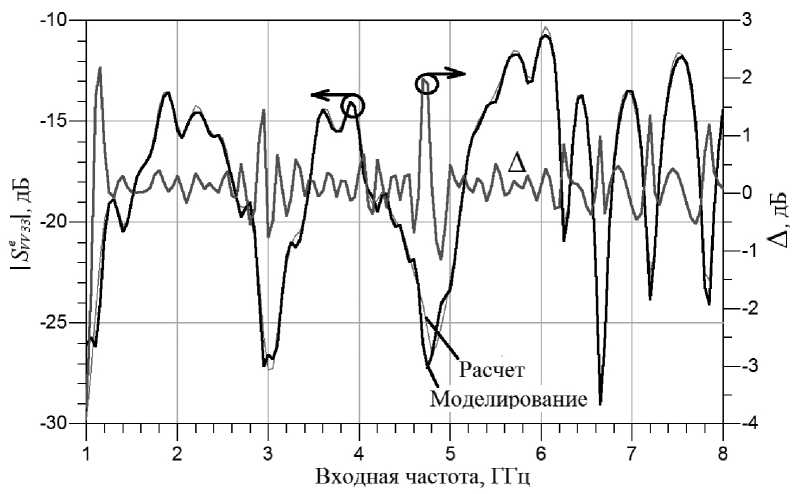
Рис. 5. Модуль выходного коэффициента отражения умножителя частоты на третьей гармонике

Моделирование технических устройств

Графики на рисунках 3–5 показывают, что представленная схема удвоителя частоты обеспечивает значение модуля выходного коэффициента отражения, не превышающее –18 дБ в диапазоне частот 2…4 ГГц по первой гармонике. Модуль выходного коэффициента отражения по второй гармонике не превышает –13 дБ в диапазоне частот 1…8 ГГц. Модуль выходного коэффициента отражения по третьей гармонике не превышает –10 дБ в диапазоне частот 1…8 ГГц. Представленная схема удвоителя по значению модуля выходного коэффициента отражения на второй гармонике превосходит представленные в [11, 13] схемы удвоителей частоты. Данные по выходным коэффициентам отражения на первой и третьей гармониках не приводятся.

На рисунках 6–8 представлены графики мощности на выходе умножителя частоты на первой, второй и третьей гармониках, рассчитанные с помощью выражений (6) и полученные путем нелинейного моделирования методом гармонического баланса в среде ADS. Графики на рисунках 6–8 получены при уровне входного сигнала 13 дБ/мВт.

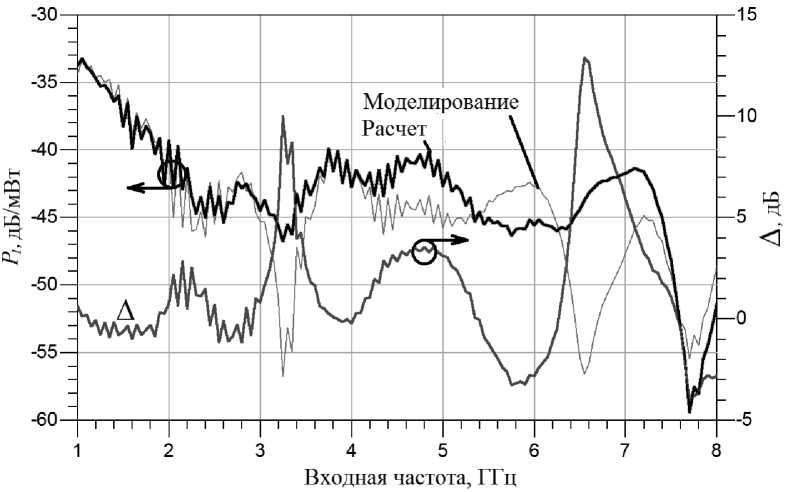
Рис. 6. Мощность сигнала первой гармоники на выходе умножителя частоты

Из рисунков 6–8 видно, что представленная схема удвоителя частоты обеспечивает подавление первой гармоники не менее 30 дБ в диапазоне частот 2…4 ГГц и не менее 20 дБ в диапазоне частот 1…8 ГГц. Подавление третьей гармоники составляет не менее 17 дБ в диапазоне частот 1…8 ГГц. Неравномерность мощности второй гармоники составляет не более 2 дБ в диапазоне частот 2…4 ГГц и не более 10 дБ в диапазоне 1…8 ГГц. Предложенная схема удвоителя частоты соответствует требованиям, представленным во введении.

Удвоитель сверхвысокой частоты на квадратурных мостах...

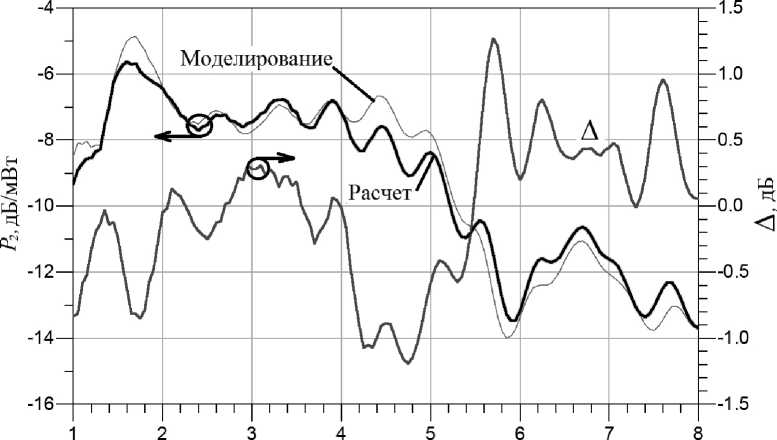
Входная частота, ГГц

Рис. 7. Мощность сигнала второй гармоники на выходе умножителя частоты

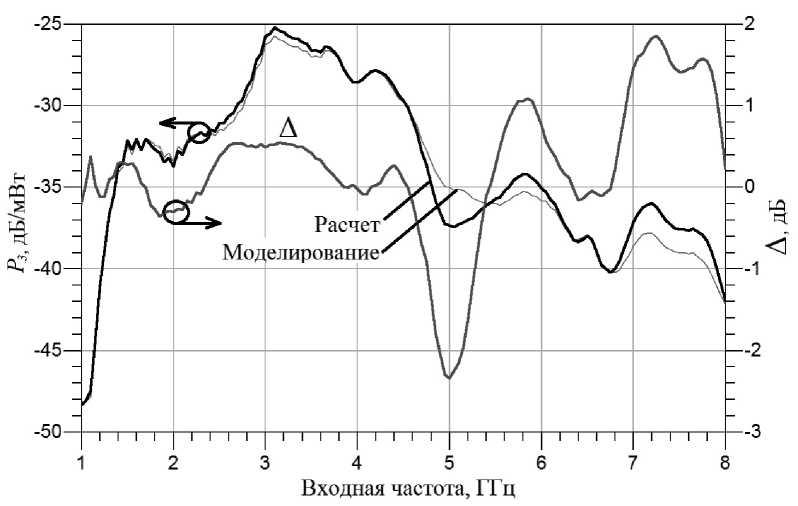
Рис. 8. Мощность сигнала третьей гармоники на выходе умножителя частоты

20 м оделирование технических устройств

Обсуждение результатов

Из выражений (2), (5), а также результатов моделирования видно, что предложенная схема умножителя частоты обладает сниженным входным и выходным коэффициентами отражения. Входной и выходной коэффициенты отражения имеют нижний предел (члены S_AA и S_VV в выражениях (2), (5)), снижение ниже которого затруднительно или невозможно. Кроме того, из выражений (4), (5) видно, что снижению коэффициентов отражения препятствует наличие фазовых и амплитудных неидентичностей пассивных устройств. Обеспечение низкого коэффициента отражения на выходе умножителя на нескольких гармониках затрудняется еще и тем, что выходные синфазные сумматоры и квадратурный преобразователь обладают ограниченной рабочей полосой. Для обеспечения низкого выходного коэффициента отражения на нескольких гармониках элементы 8 – 10 должны иметь рабочий диапазон частот, перекрывающий полосы первой, второй и третьей гармоник.

Из выражений (7)–(9) следует, что представленная схема умножителя обеспечивает подавление паразитных гармоник за счет поддержания между ними определенных фазовых и амплитудных соотношений. Ограниченная полоса рабочих частот выходных синфазных сумматоров и балансного преобразователя приводит к нарушению фазовых и амплитудных соотношений, необходимых для подавления паразитных гармоник на выходе умножителя частоты. Кроме того, дисбаланс амплитуд входных квадратурного и балансных преобразователей приводит к разнице в режимах работы транзисторов. Разница режимов работы транзисторов вызывает дополнительные амплитудные и фазовые неидентичности, что ухудшает степень подавления паразитных гармоник и снижает уровень полезного сигнала. Дополнительным фактором, снижающим амплитуду второй гармоники на выходе умножителя, является то, что составляющие второй гармоники от верхних двух плеч умножителя суммируются с составляющими от нижних двух плеч в квадратуре. Высокая неравномерность мощности второй гармоники на выходе умножителя частоты выше частоты 4 ГГц вызвана спадом коэффициента усиления транзисторов, а также влиянием паразитных параметров корпусов транзисторов. Низкий коэффициент преобразования умножителя обусловлен малым коэффициентом преобразования транзисторов, влиянием паразитных параметров корпуса транзисторов, а также потерями, вносимыми пассивными элементами 1 – 3 , 8 – 10 . Снизить влияние некоторых из указанных параметров можно переходом к монолитному интегральному исполнению умножителя частоты.

Результаты расчета и моделирования входного коэффициента отражения (рис. 2) согласуются в пределах ± 1 дБ во всем диапазоне частот. Разница в результатах расчета и моделирования выходного коэффициента отражения на первой, второй и третьей гармониках (рис. 3–5) колеблется в пределах ± 2 дБ за исключением окрестности точек, где модуль коэффициента отражения опускается ниже значения –25…–20 дБ.

Результаты расчета мощности второй и третьей гармоник на выходе умножителя частоты согласуются с результатами моделирования в пределах ± 2 дБ во всем диапазоне ча- удвоитель сверхвысокой частоты на квадратурных мостах... 21

стот за исключением окрестности точки 5 ГГц для третьей гармоники. Наибольшее расхождение наблюдается между результатами расчета и моделирования мощности первой гармоники на выходе умножителя частоты. Указанное расхождение колеблется в пределах ± 3 дБ в диапазоне частот 1…8 ГГц за исключением точек, где мощность сигнала первой гармоники падает ниже –45 дБ/мВт. Расхождение в результатах моделирования и расчета может быть связано с принятыми при разработке методики допущениями и упрощениями, учетом только однократно отраженных волн при расчете коэффициентов отражения или неучетом конечной развязки между портами балансных и квадратурных преобразователей.

Выводы

Представленная схема удвоителя частоты позволяет снизить модуль входного и выходного коэффициентов отражения до уровня –20…–10 дБ, обеспечить подавление первой и третьей гармоник не менее 20 дБ, а также обеспечить неравномерность выходной мощности в пределах 2 дБ в диапазоне входных рабочих частот 2…4 ГГц. Низкий коэффициент преобразования умножителя может быть улучшен за счет перехода к интегральной технологии изготовления.

Степень подавления паразитных гармоник, а также значения модулей коэффициентов отражения сохраняются в пределах рабочих диапазонов пассивных устройств (квадратурных ответвителей, балансных преобразователей, синфазных сумматоров). Входной и выходной коэффициенты отражения имеют нижнее предельное значение, определяемое коэффициентами отражения входного и выходного квадратурных ответвителей. Степень снижения коэффициентов отражения и степень подавления паразитных гармоник зависят от фазовой и амплитудной идентичности квадратурных мостов, балансных преобразователей, синфазных сумматоров мощности СВЧ и активных элементов. Соблюдению фазового баланса препятствует увеличение фазовой неидентичности, возникающее при умножении частоты, а также большое число пассивных фазосдвигающих устройств. Идентичность активных и пассивных устройств может быть улучшена технологическими методами (изготовление на единой подложке), однако остается разница в рабочих точках активных устройств, обусловленная амплитудной неидентичностью стоящих впереди квадратурных и балансных преобразователей.