Угловые колебания амортизируемого объекта с активной системой демпфирования

Исследование угловых колебаний амортизируемого объекта (АО) показали, что даже при больших значениях коэффициента демпфирования в элементах подвески, достигаемых как в пассивных, так и управляемых упруго-демпфируемых элементах вызываются при больших габаритах АО недопустимые величины угловых колебаний при сейсмовоздействиях [1]. В связи с этим возникает необходимость создания активной системы демпфирования продольно-угловых колебаний АО в низкочастотной области, так как частота сейсмических колебаний основания практически совпадает с собственной частотой АО. Анализ принципиальной возможности создания такой системы сделан в работе [2]. Расчетная принципиальная схема активной системы демпфирования АО с управляемыми пневмоамортизаторами (ПА) показана на рис. 1. В качестве ПА могут использоваться как многоэлементные ПА [3], так и ПА комбинированного типа с активным подводом энергии [4].

Будем полагать, что давление в ПА будет определяться системой автоматического управления процессом актив- ного демпфирования колебаний АО. В этом случае дифференциальное уравнение угловых колебаний имеет вид

Jc ϕ..+2bl2ϕ.+2cl2ϕ= c                                           .         (1)

= P1l1Sэф - P2l2Sэф -сΔlξ-bΔlξ+2c1ηl3+2b1ηl3, где Jc – момент инерции АО относительно центра масс; c – коэффициент жесткости упругой подвески 5; b – коэффициент вязкого трения в пассивных демпферах 4 (рис. 1); l1, l2 – расстояние от центра масс до линии приложения упругих и демпфирующих сил; Zc, ϕ – обобщенные координаты; ξ – вертикальные перемещения основания; η – горизонтальные перемещения основания; c1 – коэффициент жесткости горизонтальной упругой подвески 3; b1 – коэффициент вязкого трения в демпферах 2.

Система управления должна содержать измерители угловой скорости (с использованием акселерометров), которые управляют процессами наполнения и выпуска воздуха из ПА. Структурная схема системы автоматического управления показана на рис. 2. Система управления

Рис. 1. Расчетная принципиальная схема активной системы демпфирования: 1 – амортизируемый объект;

2 – горизонтальный демпфер; 3 – горизонтальный упругий элемент; 4 – демпфер; 5 – упругий элемент; 6 – основание;

7 – ПА; 8 – акселерометр; 9 – система управления заполнения и выпуска газа из ПА с РКО

работает следующим образом. При определении логическим устройством 2, что ф > 0, реле 1 включает электромагнитный клапан ЭМК-1 на подачу воздуха под давлением из ресивера в пневмоамортизатор ПА-1 и выключает электромагнитный клапан ЭМК-2, открывая выход воздуха из пневмоамортизатора ПА-2 в атмосферу. При ф < 0 реле 2 подключает через ЭМК-1 ПА-1 на выход в атмосферу и через ЭМК-2 ПА-2 подключается к ресиверу.

Постоянная времени электромагнитного клапана много меньше времени наполнения и опорожнения объема ПА [5], вследствие чего динамика процессов ПА может быть представлена в первом приближении инерционным звеном первого порядка

Время опорожнения объема ПА при тех же условиях определяется по выражению [5]

10 = ln ^min V0—, pmax RTαfc

где c =

0,58 qNRT RT

; V ₀ – объем ПА в статическом поло-

жении объекта; R – газовая постоянная.

Оценка времен t _н и t _о показывает, что постоянная времени звена первого порядка будет находиться в диапазоне t = 0,05…0,2 с в зависимости от объема используемой РКО ПА и рабочего давления.

Таким образом, система дифференциальных уравне-

к

W ( р ) = — т р + 1

ний, описывающих процесс наполнения и опорожнения объема ПА (без учета постоянной времени электромаг-

где к - коэффициент передачи; т - постоянная времени.

Будем полагать, что процессы наполнения и опорожнения объема РКО ПА происходят в надкритическом режиме, для которого справедливы следующие неравенства [5]:

pp

> £ кр и < £ кп, pр         pa    p где Р – давление в ПА; Ра – атмосферное давление; Рр – давление в ресивере.

Для адиабатического процесса при показателе адиабаты N = 1,4 и е _{к р} = 0,589, если принять, что Р _р = 1 МПа, Р _а = 0,1 МПа, то максимальное рабочее давление в ПА Р _max = 0,589 МПа, а минимальное Р _min = 0,172 МПа. При повышенном давлении в ПА Р _р = 3 МПа и Р_а = 0,1 МПа максимальное рабочее давление в ПА Р _max = 1,77 МПа при Р _min = 0,172 МПа.

Известно, что время наполнения объема ПА при изотермическом процессе определяется по выражению [5]

нитного клапана) будет иметь вид

если ф ' >  0

если ф ' <  0

т P 1 + Р = Р р , т ^Р 2 + ^Р 2 = P a ,

т Р 2 + Р 2 = Р р , т P 1 + P 1 = P a .

.    ^р max ^р min

1 =/^=, н 10αfРp TN где a = 0,7; f- площадь проходного сечения электромагнитного клапана; Т – абсолютная температура; N – показатель адиабаты.

Коэффициент жесткости РКО определяется по выражению

NPS 2 d S _с =---- эф ₊ эф р .

A V     d z

Если принять в первом приближении, что величина эф мала, а объем V является линейной функцией дz относительно перемещения, то коэффициент СА можно найти по выражению

NP 1 S эф С ~         ,

^А     h 0

где h _о – высота РКО в среднем положении.

В соответствии с последним выражением дополнительный упругий элемент (РКО ПА активной системы д емпф иров ания) имеет переменную упругость

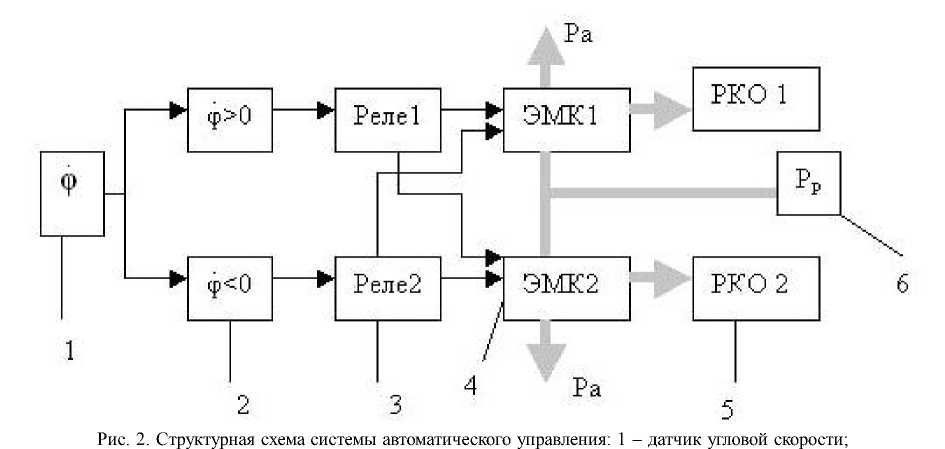
2 – логическое устройство определения; 3 – реле, переключающее подачу электрического сигнала на ЭМК-1или ЭМК-2;

4 – двухпозиционный электромагнитный клапан; 5 – ПА; 6 – ресивер системы подачи давления газа в ПА ( Р _а – атмосферное давление, Р _р – давление в ресивере)

и уравнение (1) с уч етом того, что L ₁ = L ₂ = L , пр имет вид

1 c ф"+ 2 bl ²ф'+ 2 1²

-

c +

NS эф h ₀

( P i + P 2 )

NS эф

( P 1 + P 2 )

= 1S эф ( P i + P 2 ) -

A 1 ^ + b A 1 ^'+ 2 qn 1 3 + 2 b i n' 1 3

Таким образом, уравнение (4) совместно с системой уравнений (3) достаточно адекватно будет описывать процесс развития угловых колебаний в АО с активной системой демпфирования.

Для анализа нелинейных уравнений (3) и (4) примем, что упруго-демпфирующая подвеска имеет коэффициент жесткости много больше, чем дополнительно устанавливаемые ПА, а процесс наполнения и опорожнения объема ПА в надкритическом режиме происходит по

одинаковому закону.

Управляющее звено в первом приближении можно представить в виде идеального релейного элемента

^( Ф ') = X max^si g ⁿ ф ',

где х _max– амплитуда перемещения релейного элемента.

При использовании акселерометров в схеме управления после интегратора установлен фильтр, передаточную функцию которого можно представить в виде

T

p p Tp + 1, где Т – постоянная времени фильтра. Фильтр подобного вида исключает ошибку из сигнала датчика, которая возникает в результате интегрирования погрешности акселерометра из-за зоны нечувствительности и неопределенности в определении центра тяжести, что может приводить к появлению в структуре полезного сигнала медленно меняющейся погрешности. С учетом вышеизложенного уравнение (4) запишем в виде

Ф '' ⁺ k 2 Ф ' ^{+ k} 1 Ф⁺ / 1⁽ ф ') = f ⁽ t ),               ⁽⁵⁾

где f1(ф') = W), F1(ф) = 1SЭф(Pi + P2), ki = _ lc k2 = 2^ю0 f (t) = — (cA1 ^ + bA1 ^'+ 2c13n + 2b13 n )

I c

Структурная схема колебательной системы, соответствующей АО на упруго-демпфирующем подвесе с активной системой демпфирования в случае точного измерения угловой скорости приведена на рис. 3.

Приближенное исследование движений нелинейной системы (рис. 3) выполнено с помощью метода гармонической линеаризации [6]. Для идеального реле можно записать следующее:

x = q Ф ',

4x где q = —'—, фмах - амплитуда координаты ф. пфтах

Коэффициент линеаризации q определен в соответствии с характеристикой идеального реле.

В соответствии со структурной схемой (рис. 3) передаточная функция линеаризованной системы демпфирования угловых колебаний будет иметь вид

W ( p ) = 774 =

f ( p )

=                                                  .       (6)

т p ³ + (i + к ₂ т ) p ₂ + ( k ₂ + k _i T + qk 3 ) p + k _i

В нелинейной системе с релейным элементом возможны режимы с автоколебаниями. Анализ и оценка возможности возникновения автоколебаний [6] показали, что в данной системе автоколебания не возникают.

Определение вынужденных колебаний произведем для внешних воздействий вида f (t) = B sin tobt, где В и wо – амплитуда и частота внешнего воздействия.

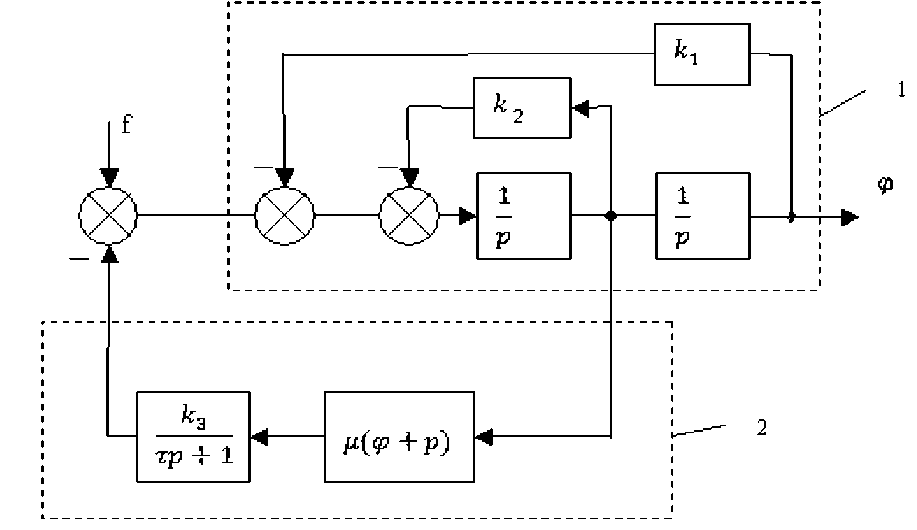
Рис. 3. Структурная схема колебательной системы: 1 – АО на упруго-демпфирующем подвесе; 2 – активная система демпфирования угловых колебаний

Вынужденные колебания АО представим в виде ϕ=ϕ _m sin( ω _Bt +a ).

Относительная оценка эффективности активной системы демпфирования при периодическом внешнем воздействии может быть произведена по коэффициенту η :

^ϕ max 0

η= 0 , где ϕmax – амплитуда вынужденных колеба-ϕmax ний при выключенной активной системе.

Результаты расчета коэффициента h для следующих значений параметров показаны на рис. 4: K ₁ = 49 1/c², K ₂ = 7 1/c, K ₃ = 70 1/c, B = 100 1/c², x_m = 1 и различных значениях постоянной времени τ .

Графическая зависимость η = f ( w _в) показывает, что наиболее эффективно активная система функционирует при совпадении частоты вынужденных колебаний с частотой собственных колебаний (отметим, что для любых пассивных систем демпфирования этот случай – наиболее неблагоприятный вариант).

Анализ показал, что можно всегда подобрать такие величины параметров х_m, K ₃. Это соответствует выбору ПА с заданной грузоподъемностью, при которых будет достигаться минимальное значение коэффициента η . Необходимо подчеркнуть, что при сейсмовоздействиях на АО колебания основания (грунта) происходят с частотой близкой к величине 1 Гц, что практически совпадает с собственной частотой АО.

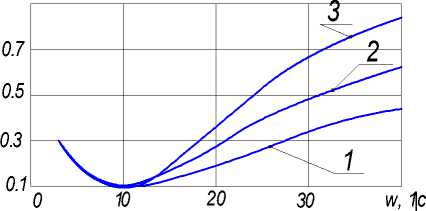
Рис. 4. Зависимости коэффициентов демпфирования от частоты: 1 – τ = 0,05; 2 – τ = 0,1; 3 – τ = 0,2

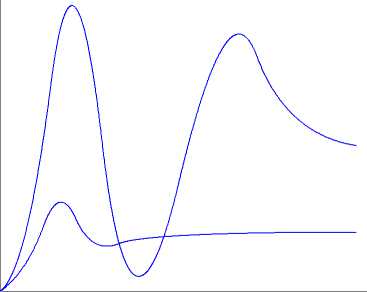
С целью анализа влияния сейсмовоздействий на угловые колебания АО с активной системой демпфирования решение системы нелинейных уравнений произведено с помощью прикладной программы MATLAB c расширением Simulink . Результаты расчета для различных значений x , K ₃ и t приведены на рис. 5–6.

При сейсмовоздействиях величина амплитуды колебания по углу ϕ может быть уменьшена по сравнению с АО без активной системы в три раза, а вторые и последующие амплитуды колебаний на порядок и более . При этом, чем меньше величина τ , тем эффективнее работа активной системы, а величина K ₃ может быть выбрана для рассматриваемой системы в пределах K ₃ = 1,2…1,5. Подобные величины K ₃ соответствуют включению дополнительного ПА с грузоподъемностью 6 × 10⁴ Н и рабочим ходом, равным рабочему ходу ПА штатной системы амортизации АО.

Таким образом, можно сделать следующие выводы: активная система демпфирования угловых колебаний АО при гармонических воздействиях наиболее эффективна в низкочастотной области и при малых коэффициентах демпфирования штатной подвески; при сейсмовоздействиях непрерывно действующая активная система демпфирования снижает амплитуду первого колебания в несколько раз и последующих колебаний на порядок.

ф, рад

0.0 16

0.0 14

0.0 12

0.0 1

0.0 0 8

0.0 0 6

0.0 0 4

0. 0 0 2

0                 0.5                  1

1.5               2

Рис. 5. Угловые колебания АО при сейсмовоздействии: w _o = 7, К ₃ = 0,7, ξ = 0,5, τ = 0,1 с

t ,c

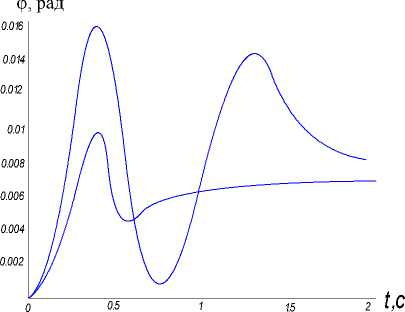
Рис. 6. Угловые колебания АО при сейсмовоздействии: w _o = 7, К ₃ = 0,7, ξ = 0,5, τ = 0,2 с