Угловые колебания амортизируемого объекта с пассивной системой демпфирования

Особое место при анализе динамики амортизируемых объектов (АО) занимают угловые движения. Крупногабаритный объект можно рассматривать в первом приближении как абсолютно твердое тело на упругом подвесе, а возмущение, действующее на объект со стороны основания, как кинематическое возмущение. В этом случае, как это следует из справочника [1], для простейшего одномерного случая прямолинейного движе- ния и при кинематическом гармоническом возмущении со стороны основания цель защиты объекта может заключаться в уменьшении амплитуды абсолютного ускорения (перегрузки) объекта. Степень реализации цели характеризуется безразмерным коэффициентом эффективности К:

К = a / (w2 хо), где a – ускорение объекта; w – частота возмущения; xo– амплитуда возмущения.

С учетом безразмерных параметров z = w / w _o и n = n / w _o, где w _o– собственная частота колебаний объекта; n – коэффициент демпфирования в подвеске объекта. Коэффициент К имеет вид

1 + 4 u ² z ^{2 К =} (1 - z ²)² + 4 u ² z ^2.

Величина К ≤ 1 обеспечивается в частотном диапазоне z ≥ √ 2. При этом эффективность виброизоляции выше, если подвес обладает малым демпфированием и, естественно, для этого случая идеальным будет подвес с n = 0. Отметим, что все вышесказанное относится, при сделанных предположениях, и к угловым колебаниям. Однако при негармонических воздействиях (типа ударная волна и т. д.) приходится разрешать очевидные противоречия:

– слабое демпфирование обеспечивает хорошую виброизоляцию при длительных гармонических воздействиях (т. е. при рассмотрении только установившихся колебаний объекта), но при единичных воздействиях в такой системе могут возникать колебания со значительной амплитудой на собственной частоте w _o;

– увеличение коэффициента демпфирования наряду с уменьшением амплитуды собственных колебаний повышает величину усилия, передающегося из-за движения основания на объект через упругий подвес с демпфированием.

Вследствие вышеизложенного, решение проблемы амортизации объекта с кинематическим возбуждением представляет всегда компромиссную задачу. Эта задача, для пассивных упруго-демпфирующих элементов подвеса, решается подбором оптимальных значений коэффициентов упругости и демпфирования и может быть успешно решена для любого вида кинематического воздействия введением управляемой виброзащиты (активных виброзащитных систем) [2].

При исследовании угловых движений объекта в первом приближении можно рассматривать только плоское движение, так как взаимовлияние колебаний достаточно мало. Расчетная схема для анализа движения объекта в случае пассивных упруго-демпфирующих элементов представлена на рис. 1.

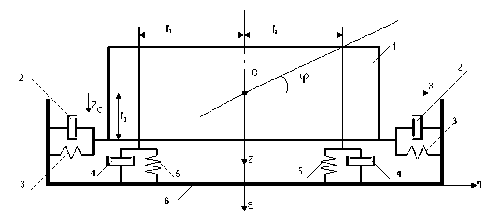
Рис. 1. Расчетная схема подвеса объекта: 1 – амортизируемый объект; 2 – горизонтальный демпфер; 3 – горизонтальный упругий элемент; 4 – демпфер; 5 – упругий элемент;

6 – основание

При составлении дифференциальных уравнений движения будем полагать, что в статическом положении сила тяжести тела с массой m уравновешена силами упругос- ти, координата Zс отсчитывается от положения равновесия, движение по координате Х не рассматривается. При таких предположениях и в случае упругих элементов с линейной нагрузочной характеристикой дифференциальные уравнения малых движений можно записать в следующем виде:

mz c =- b ( z 1 + z ₂) - c ( z ₁ + z ₂);

J_c ϕ=- bl ₁ z 1 + bl ₂ z 2 - cl ₁ z ₁ + cl ₂ z ₂ ⁺ η⋅ 2 cl ₃ +η⋅ 2 bl ₃;

z ₁ = z_c +ϕ l ₁ -ξ ;

z ₂ = z_c -ϕ l ₂ -ξ ,                 (1)

где J_c – момент инерции объекта относительно центра масс; c – коэффициент жесткости упругой подвески 5 ; b – коэффициент вязкого трения в пассивных демпферах 4; l ₁, l ₂ – расстояния от центра масс до линии приложения упругих и демпфирующих сил; Z _c, ϕ – обобщенные координаты; ξ – вертикальные перемещения основания; η – горизонтальные перемещения основания; c ₁ – коэффициент жесткости горизонтальной упругой подвески; b ₁ – коэффициент вязкого трения в демпферах 2 .

Компоновка амортизируемого объекта обычно тако- ва, что центр масс практически совпадает с центром уп- ругости от элементов 5 и, как показывает проведенное исследование уравнений (1), при неподвижном основа- нии (ξ = 0, ξ = 0) коэффициенты связи продольно-угловых и вертикальных колебаний малы и можно принять допущение о независимости продольных угловых колебаний от вертикальных. В этом случае угловые колебания будут описываться дифференциальным уравнением

J_c ϕ+ 2 bl ² ϕ+ 2 cl ² ϕ =

=-cΔlξ-bΔlξ.+2c1ηl3+2b1η.l3, где Δl = l1 – l2 , или приводя к нормальному виду получим ϕ+2ξω0ϕ+ω02ϕ=-n1ξ-n2ξ+d1η+d2η,(3)

где ω ² ₀ =

2 c ₁ l ₃ d ₁ =        ;

Jc

J ;  2ξω0 = c    2b1l3

d =       .

2 _{J c}

2 bl ² _; J_c

cΔl n1=     ;   n2=

Jc

Динамика угловых колебаний для математической модели в соответствии с уравнением (3) определена для следующих параметров объекта:

L = 12 м; L ₃ = 3 м; С = 1 500 кН/м; Р = mg = 1,55 ⋅ 10³ кН;

J_c = 8,731 ⋅ 10⁶ кГ ⋅ м²; w ₀= 7,03 1/с; ξ = 0,5–0,7 м; Δ L = 2 м.

Параметры возмущения заданы в виде перемещения ξ основания при сейсмическом воздействии в соответствии с экспериментальным графиком записи перемещения основания (рис. 2).

Оценка угловых колебаний произведена численным интегрированием уравнения (3) правой части с помощью прикладной программы Matlab (рис. 2). Результат решения выражения (3) при сейсмовоздействии показан на рис. 3:

ξ *10^–2, м.

Численное решение уравнений и их анализ в среде Matlab при различных значениях коэффициентов ξ , С и С ₁, массы амортизируемого объекта, размеров L и L ₃ показали, что при сейсмовоздействиях амплитуда колебаний по углу ϕ лежит в пределах 0,01…0,02 рад

(0,57…1,14о). Таким образом, вариации параметров пассивных элементов системы подвеса амортизируемых объектов не меняют существенно величин угловых коле-

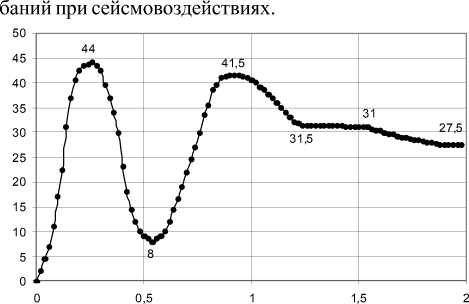
Рис. 2. График перемещения о снования

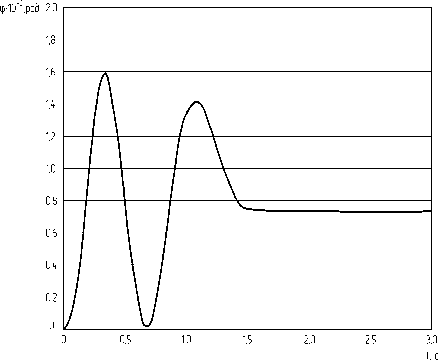
Рис. 3. График угловых колебаний АО

На основе анализа технических характеристик амортизирующего устройства разработки КБСМ (Санкт-Петербург) (максимальная грузоподъемность ≥ 300 т; максимальный рабочий ход по вертикали +350 мм) видно, что при сравнительно больших размерах объекта ход амортизатора по вертикали будет определяться суммой вертикального перемещения центра масс Zo и узлов крепления амортизаторов ϕL. При L > 10 м ход амортизатора будет превышать максимальный рабочий ход (+350 мм) данного амортизирующего устройства, что будет приводить к пробоям амортизаторов (ударамоб упоры).

Для улучшения работы амортизирующих устройств по угловым движениям целесообразно применять активные устройства. Их использование в транспортных средствах [3] и для угловой стабилизации объектов [4] дает хорошие результаты.

Таким образом, угловые колебания амортизируемого объекта cо штатной системой упруго-демпфирующей подвески при сейсмических воздействиях могут достигать величин, при которых прямолинейные перемещения упругих элементов (совместно с вертикальными перемещениями) превышают допустимые значения, поэтому для улучшения работы амортизирующих устройств по угловым движениям целесообразно применять активные устройства демпфирования колебаний.