Ultra Encryption Standard Modified (UES) Version-I: Symmetric Key Cryptosystem with Multiple Encryption and Randomized Vernam Key Using Generalized Modified Vernam Cipher Method, Permutation Method, and Columnar Transposition Method

Published Online July 2012 in MECS DOI: 10.5815/ijmecs.2012.07.05

The last one decade now it is a real challenge to all of us to send confidential data/information from one computer to another computer. The massive growth in communication technologies and the tremendous growth in internet technology in the last decade have made it a real challenge for a sender to send confidential data from one computer to another. When a sender is sending some data from one computer to another computer then in between there may be a middle man attack and the data may be diverted to different places. If the data is not properly encrypted or protected then the receiver may not always get correct data. The security of data has now become a big issue in data communication network. If we send any important message from one computer to another through the internet, then, an intruder might intercept that confidential/important message. The teachers send question papers through e-mail. This is no more a safe method now as the hackers may intercept it any time. It is not a difficult job for a hacker to intercept that mail and retrieve the question paper if it is not encrypted. In banking sectors the financial data must be secured if by chance the data goes to the hacker then the entire banking service may collapse. Weak password breaking is now not a problem. Many public software are available to decode password of some unknown email. Suppose in some financial transaction the hacker retrieves the password and after that what he can do is quite understandable. It must be ensured that, when a client is sending some confidential data from the client machine to another client machine or from the client machine to the server, then that data should not be intercepted by someone. The data must be protected from any unwanted intruder otherwise a massive disaster may take place. Suppose an intruder intercepts the confidential data of a company and sells it to a rival company, then it will be a big damage for the company from where the data has been intercepted. Because of this hacking problem now the network security and cryptography is an emerging research area where the people are trying to develop some good encryption algorithm so that no intruder can intercept the encrypted message. Cryptography algorithms are of two types (i) Symmetric key cryptography where we use single key for encryption and decryption purpose. And (ii) Public key cryptography where we use one key for encryption purpose and one key for decryption purpose.. Both the methods have their advantages as well as disadvantages. Nath et al. had developed some advanced symmetric key algorithm [1-8]. In the present work we are proposing a symmetric key method called Modified UES version-I which is a combination of 3 distinct cryptographic methods, namely, (i) Generalized Modified Vernam Cipher Method, (ii) Permutation method and (iii)Columnar transposition method with features like multiple encryption, randomized Vernam key and multiple sequence of column extraction. We have tested this method on various types of known text files and we have found that, even if there is repetition in the input file, the encrypted file contains no repetition of patterns. In results section we have shown various known plain text and the corresponding encrypted text.

• II.    MODIFIED UES VERSION-I ALGORITHM

Modified UES version-I has incorporated additional features like multiple encryption and randomized Vernam key generation and multiple sequences of extraction of columns on the Columnar Transposition, Modified Vernam Cipher and Randomization methods to make the encryption extremely strong ensuring no repetition of patterns.

Multiple Encryption : The plain file is encrypted a number of times to generate a cipher file which is very strongly encrypted. This increases security and it will be very hard to crack the cipher code even through immense brute force.

Randomized Key Generation : The password key for the UES is generated by a mathematical calculation, taking the ASCII codes of the 64-bit password (given by the user) into consideration. The key constructed is of 900 bytes. This key is randomized using the basic techniques employed by the randomization algorithm. The randomized key will enable the encryption to be even stronger.

Multiple sequence of column extraction: In each iteration, the algorithm generates a sequence of column extraction from the 64-byte user password. In every iteration, three distinct levels of encryption are implemented namely Modified Vernam Cipher with feedback,     Columnar     Transposition     and

Randomization/Permutation Encryption Process (in that order). The encryption is performed in blocks of 900 bytes. The residual bytes (of size less than 900 bytes) are encrypted with the Modified Vernam Cipher Encryption Method. The algorithm may handle files of all formats and sizes.

Algorithm for the integration of the three levels of encryption:

Step 1: Start

Step 2: Input the plain text file name in ‘plain []' (The plain file may be of any format).

Step 3: Input the cipher text file name in ‘cipher []'

Step4: The extracts the first byte in the file and stores it in 'ch' and it extracts the last byte of the file and stores in 'cha'. It replaces the first byte of the file with character with ASCII (ch+cha) %256.

Step 5: The user enters a 64 byte encryption-key that is stored in ‘key []'.

Step 6: Compute cod=key[i]*(i+1) where i represents the position of every character in the key.

Step 7: Compute encryption number enc = mod (cod, 17). If enc <0 then enc=7

Step 8: Take the input file pointer to the end of the input file, such that the size of the input file can be computed. (The size of the input file is stored in long integer variable'n'.)

Step 9: Declare a variable 'n1' of long int data type where n1 will store the number of iterations. Each iteration will process a 30 X 30 bytes block in every iteration of encryption.

Step 10: Introduce a variable p=0 and compute cod=cod modulus 256.

Step 11: If p is greater than or equal to enc then GOTO 19.

Step 12: Increment cod and perform cod=cod%256.

Step 13: Now create a key file by printing the characters with ASCII values of 0-255 in rotation. The first character is however the character with ASCII

'cod'. This key file serves as the input for the Modified Vernam Cipher with feedback.

Step 14: This key is further randomized using randomization module and stored in the file 'file1.c'.

Step 15: Initialize integer variable count to 0.

Step 16: If count greater than or equal to n1 then Goto 25.

Step 17: Define the intermediate file which will open, extract and process the first 900 bytes of the plain file.

Step 18: The 900 bytes that have been extracted is now encrypted with the Modified Vernam Encryption process with Feedback

Step 19: The output from the modified vernam cipher encryption process is fed as input to the columnar transposition encryption process.

Step 20: The output from the columnar encryption method will now undergo randomization/permutation encryption method.

Step 21: The output file from the randomization process holds the encrypted 900 bytes.

Step 22: The 900 bytes is written to the cipher file name provided by the user.

Step 23: The value of 'count' is incremented by 1. Goto 17.

Step 24: Once the control breaks from the loop, the program is left to process the residual bytes from the input file.

Step 25: The residual bytes are processed by the modified Vernam cipher encryption technique. The encrypted bits are again written into the cipher file which serves as the input for the next iterations of encryption.

Step 26: Increment p

Step 27: Goto 12

Step 28: When the control reaches this encryption the Modified Vernam Cipher, Columnar Transposition and Randomization modules are complete. We obtain the Cipher file.

Step 29: The output is again written back to the cipher file whose name is provided by the user.

Step 30: End

Algorithm for the first level of encryption - Modified Vernam cipher encryption method with feedback.

Step 1: Start

Step 2: The plain text serves as the input file for the program.

Step 3: Create a dictionary of characters in the character array where position i will be the ASCII value for the character placed in the i-th location of the array.

Step 4: Define the encryption key which must be same as the key provided during decryption.

Step 5: Start processing the characters in the input file. Define a integer variable 'feed' and initialize it with 0.

Step 6: Extract a character in the input file and store in ch1. If ch1is NULL, goto 12

Step 7: Extract a single character from the key file.

Step 8: Compute m,n from the arrays arr[] where m and n are the ASCII values for the first characters of the input file and key files respectively.

Table 1: Modified Vernam Cipher Method Key: abc

Plain text:	a	a	a
Plain Index(m):	97	97	97
Key text:	a	b	c
Key Index(n):	97	98	99
Feedback (feed):	0	194	133
m=m+n+feed	194	389	329
n=m%256	194	133	73
Cipher text:	т	à	I

Step 10: Write the contents of the array in the intermediate output file one by one, where the array in the n-th place of the array is the encrypted character.

Step 11: Goto 7.

Step 12: Once the control comes out of the loop, the encryption process is complete.

Step 13: END

Algorithm for the second level of encryption-Columnar Transposition Method

Step 1: Start

Step 2: Now the algorithm extracts the first character of the 'file1.c' in 'cha' and computes 'od'=cha modulus 6. The value of od determines the sequence of columns everytime the columnar module is invoked.

Step 3: Now we compute the array 'arra[]' where the first entry is od. Then 'od' is subsequentely decremented. If the value of od becomes 0 then it is replaced by 5. This array decided the definite order of the sequence of columns extracted.

Step 4: The 900 bytes of output from the Modified Vernam Method serves as the input file for Columnar Transposition Method.

Step 5: Initialize the variable n to an arbitrary integer value which represents the number of columns of the columnar transposition array in which the plain file characters will be stored. Typically n may have any value.

Step 6: Initialize both integer variables 'row' and 'col' to 0

Step 7: Initialize all the elements in the specified array arr[][] to NULL('\0')

Step 8: Store the plain text file byte by byte in the array arr[][] where the row and column positions are determined by 'row' and 'col'.

Step 9: Increment column index by 1 once a byte is read and placed in the array

Step 10: If col is equal to n then increment row by 1 and intialize col variable to 0 to keep a check on the row and column parameters.

Step 11: Goto 9 until the storing of the intermediate plain text in the array is complete.

Step 13 Initialize both variables 'count' and 'index' to 0.

Step 14: If (count>=n) goto 17

Table-II (a): Plain Text

0	1	2	3	4	5
l	e	t	s	a	l
l	g	o	n	o	w

Plain text: Letsallgonow

The plain text is placed in array ‘arr’. arra[]={5,4,3,2,1,0} (assume) p=arra[index](where index=0 and subsequently index=index+1)

p=5, 4, 3,2,1,0 respectively where p stands for the extracted column. Table-II(b): Cipher Text

Table II (b): Columnar Transposition Cipher Text:lwaosntoegll

0	1	2	3	4	5
l	W	A	O	S	N
t	O	E	G	L	L

Step 15: Count is incremented by 1

Step 16: Initialize variable p to arra[index]. Here the 'arra[]' stores the order in which the columns will be transported to the same columnar transposition array arr[] to implement the columnar transposition encryption method. The variable 'index' is subsequently incremented to transport the rest of the columns of the columnar transposition array

Step 17: End

Algorithm for the third level of encryptionRandomization / Permutation Method

Step 1: Start

Step 2: The output from the columnar transposition method serves as the input for the randomization/permutation process.

Step 3: Define integer arrays 'arr' that will store the randomization key. Define 2-d character arrays 'chararr[][]to store all the 900 bytes in the file and chararr2[][] to store the randomized characters.

Step 4: Initialize all the elements in the character arrays chararr [][] and chararr2[][] to 'null'.

Step 5: Initialize m to 30 and n to 1. 'm' holds the number of rows and columns in the square matrix of chararr[][],chararr2[][], arr[][].

Step 6: Input the numbers 1, 2, 3..., 900 to the integer array arr [][] by incrementing the value of n. The characters in the input file are copied to the character array ‘chararr []'.

Step 7: Now randomize the numbers in the integer array with the help of the functions defined in the program.

Step 8: The program invokes function 'leftshift()' which shifts every column in the integer array to one place left thus the first column is displaced to the position of the last column.

Step 9: Invoke function 'topshift() which shifts very row to the row above. Therefore the elements in first row are displaced in the corresponding position of the last row.

Step 10: Subsequently perform cycling operation on the integer array ‘arr [][]' . Intialize i to 1.

Step 11: If i is greater than m/2 Goto 15.

Step 12: If i is odd, perform clockwise cycling of the i-th cycle of the character array. Invoke functions rights(),downs(), lefts(),tops() to implement the clockwise displacement of the elements in arr[][].

Step 13: If i is even, perform anti-clockwise cycling of the i-th cycle of the character array.

Invoke functions ac_rights(), ac_downs(), ac_lefts(), ac_tops() to implement the anti-clockwise displacement of the elements in arr[][]. Therefore the integer array arr[][] is alternately randomized in clockwise and anit-clockwise cycles.

Step 14: Increment i. Goto 11.

Step 15: The program invokes function 'rightshift()' which shifts every column in the integer array to one place right thus the last column is displaced to the position of the first column.

Step 16: Invoke function ‘downshift () which shifts very row to the row below. Therefore the elements last row is displaced in the corresponding position of the first row.

Step 17: Invoke the function 'left diagonal ()' that performs downshift on the elements in the left diagonal such that the lowermost element is displaced to the position of the topmost element in the left diagonal.

Step 18: Invoke the function ‘rightdiagonal ()' that performs downshift on the elements in the right diagonal such that the lowermost element is displaced to the position of the topmost element in the right diagonal.

Step 19: To arrange the elements in the character array chararr[][] according to the randomized integer array arr[][]. Initialize i to 1.

Step 19: Initialize j to 1

Step 20: Store element arr[i][j] in z.

Step 21: Compute the row and column position pointed by the element z which is stored in 'k','l' respectively.

Step 22: Place chararr[k][l] in auxiliary character array chararr2[][] in positions chararr2[i][j].

Step 23: Increment j.

Step 24: If j<=m goto 20

Step 25: Increment i

Step 26: If j<=m goto 20

Step 27: Write the randomized elements in character array chararr2 [i][j] to the intermediate output file.

• III.    DECRYPTION PROCESS:

The decryption algorithm follows the reverse process of the three levels of encryption that have been implemented. Therefore in every iteration, the three of decryption      processes       employed      are

Randomization/Permutation Decryption Method, Columnar Transposition Decryption Method and Modified Vernam Cipher Decryption with feedback (in the specified order). Again, the algorithm performs the decryption in blocks of 900 bytes and the residual bytes of the cipher file (size less than 900 bytes) are processed with the Modified Vernam Decryption Method with feedback.

Algorithm of Integration of the three levels of Decryption Methods:

Step 1: Enter the name of the encrypted file.

Step 2: Enter the name of the decrypted file.

Step 3: Decrypt the cipher file using the encryption methods in reverse order.

Step 4: Enter the 64 byte character key.

Step 5:  Compute cod=summation (key[i]*(i+1))

where i represents the positional value of character. Compute the encryption number from the 64 byte key entered by the user where enc=cod%7.

Step 6: If enc<7 then enc=7

Step 7: Compute n1 where n1where each iteration will encrypt a block of 900 bytes.

Step 8: Declare p=0

Step 9: If p>=enc GOTO 21

Step 10: Generate the randomized key for the modified Vernam Cipher.

Step 11:Declare count=0

Step 12:if count=n1 then GOTO 13

Step 13:Feed the 900 byte block to the Randomization Module.

Step 14:The output from the Randomization Module is fed as input to the Columnar Transposition Method

Step 15:  The output from the columnar

Transposition Method is fed as input to the Modified Vernam Cipher with feedback.

Step 16: The output from the Vernam module is written into the cipher file. Increment count. Goto 12

Step 17: Once the control flows out of the loop, the residual bytes (that is less than 900 bytes file size) are processed by Modified Vernam Cipher with feedback.

Step 18: The encrypted residual bytes are written into the cipher file.

Step 19: The cipher file is now treated as the plain input file to enable successive encryption. Increment p.

Step 20: GOTO 9

Step 21: When the control flow is out of the loop we readjust the first character in the decrypted file where the ASCII of the first byte is replaced by the difference of the ASCII of the first and last byte to get the final decrypted file.

Step 22: End

Algorithm for the first level of decryption Randomization / Permutation Decryption Method:

Step 1: Start

Step 2: The program processes the 900 bytes of the decrypted file as the input file.

Step 3: Define integer arrays 'arr' that will store the randomized key. Define 2-d character arrays 'chararr[][]' to store all the 900 bytes in the encrypted file and chararr2[][] to store the decrypted characters.

Step 4: Initialize all the elements in the character arrays chararr [][] and chararr2[][] to 'null'.

Step 5: Initialize m to 30 and n to 1. 'm' holds the number of rows and columns in the square matrix of chararr[][],chararr2[][], arr[][].

Step 6: Input the numbers 1,2,3...,900 to the integer array arr[][] by incrementing the value of n. The characters in the input file are copied to the character array 'chararr[]'.

Step 7: Now de-randomize the characters in the array chararr [][] we use the numbers in the randomized integer array made with the help of the functions subsequently defined in the program.

Step 8: The program invokes function 'leftshift()' which shifts every column in the integer array to one place left thus the first column is displaced to the position of the last column.

Step 9: Invoke function 'topshift() which shifts every row to the row above. Therefore the elements in first row are displaced in the corresponding position of the last row.

Step 10: Perform cycling operation on the integer array 'arr[][]' . Initialize i to 1.

Step 11: If i is greater than m/2 goto 15.

Step 12: If i is odd, perform clockwise cycling of the i-th cycle of the character array. Invoke functions rights(),downs(), lefts(),tops() to implement the clockwise displacement of the elements in arr[][].

Step 13: If i is even, perform anti-clockwise cycling of the i-th cycle of the character array. Invoke functions ac_rights(), ac_downs(), ac_lefts(), ac_tops() to implement the anti-clockwise displacement of the elements in arr[][]. Therefore the integer array arr[][] is alternately randomized in clockwise and anit-clockwise cycles.

Step 14: Increment i. Goto 11.

Step 15: The program invokes function 'rightshift()' which shifts every column in the integer array to one place right thus the last column is displaced to the position of the first column.

Step 16: Invoke function 'downshift() which shifts very row to the row below. Therefore the elements last row is displaced in the corresponding position of the first row.

Step 17: Invoke the function 'leftdiagonal()' that performs downshift on the elements in the left diagonal such that the lowermost element is displaced to the position of the topmost element in the left diagonal.

Step 18: Invoke the function 'rightdiagonal()' that performs downshift on the elements in the right diagonal such that the lowermost element is displaced to the position of the topmost element in the right diagonal.

Step 19: To de-randomize the elements in the character array chararr[][] we utilize the integer array arr[][]. The decrypted characters are stored in auxilliary character array chararr2[].Initialize i to 1.

Step 20: Initialize j to 1

Step 21: Initialize integer variables flag to 0, k to 0 and l to 0.

Step 22: if arr[k][l] is not equal to n goto 24

Step 23: chararr2[i][j] assumes the value in chararr[k][l], flag=1 and BREAK.

Step 24: If 'flag' is equal to 1 break

Step 25: Increment l.

Step 26: If l is less than or equal to m goto 22.

Step 27: Increment k

Step 28: If k is less than or equal to m goto 22.

Step 29: Increment n.

Step 30. Increment j.

Step 31. If j is less than or equal to m goto 21.

Step 32. Increment i

Step 33: If i is less than or equal to m goto 22.

Step 34: Write the decrypted elements in the character array chararr2 [][] in the intermediate output file.

Step 35: End

Algorithm for the second level of Decryption -Columnar Transposition Decryption Method

Step 1: Start

Step 2: Now the algorithm extracts the first character of the 'file1.c' in 'cha' and computes 'od'=cha modulus 6. The value of od determines the sequence of columns everytime the columnar module is invoked.

Step 3:Now we compute the array 'arra[]' where the first entry is od. Then 'od' is subsequentely decremented. If the value of od becomes 0 then it is replaced by 5. This array decided the definite order of the sequence of columns extracted.

Step 4:The 900 bytes of output from the

Randomization/Permutation serves as the input file for Columnar Transposition Method.

Step 5: Declare 'count' which stores the size of the file.

Step 6: Compute 'no' where no is equal to count modulus 6 (where 6 is the number of columns in this case).

Step 7: If count modulus 6 is 0 then increment 'no'.

Step 8: Declare i=0

Step 9: The encrypted file is now transferred to an array.

Step 10: If i is greater than or equal to 6 then GOTO 17

Step 11: Define p=num[i] and k=0

Step 12: If k is greater than or equal to 'no' GOTO 16

Step 13: Write the character of the cipher file in an array.

Step 14: Increment k

Step 15: GOTO 12

Step 16: Increment i. GOTO 10

Step 17: The array is written row-wise to yield the decrypted file.

Step 18: End

Algorithm for the third level of decryption- Modified Vernam Cipher Decryption with feedback

Step 1: Start

Step 2: The output from the columnar transposition method serves as the input file for the decryption program.

Step 3: Create a dictionary of characters in the character array arr[] where i will be the ASCII value for character arr[i].

Step 4: Define decryption key which must be same as the key provided during encryption.

Step 5: Start processing the characters in the encrypted input file.

Step 6: Extract the first character in the input file and the key files and store in ch1, ch2.

Step 7: Compute m and n from the dictionary of characters where m is the ASCII for ch1 and n is the ASCII for ch2. Perform n=m-n.

Step 8: If n is less than 0 then n=n+256. Here the character arr[n] serves as the first decrypted character.

Step 9: Extract the subsequent character in the encrypted input file and store in character variable 'ch1'. If ch1 is NULL Goto 19

Step 10: Store the next character from the key file in ch2.

Step 11: Store the ASCII for ch1 in integer variables 'p' and 'r'.

Step 12: Store the ASCII for ch2 in integer variable 'q'.

Step 13: Compute p=p-(q+m).

Step 14: Compute p=p+256

Step 15: If p is less than 0 Goto 14

Step 16: The integer variable 'p' is the ASCII for the decrypted character. Write arr[p] in the output file whose name is provided by the user.

Step 17: Assign the value of 'r' to 'm'.

Step 18: Goto 9.

Step 19: Once the control comes out of the loop, decryption is complete.

Step 20: End

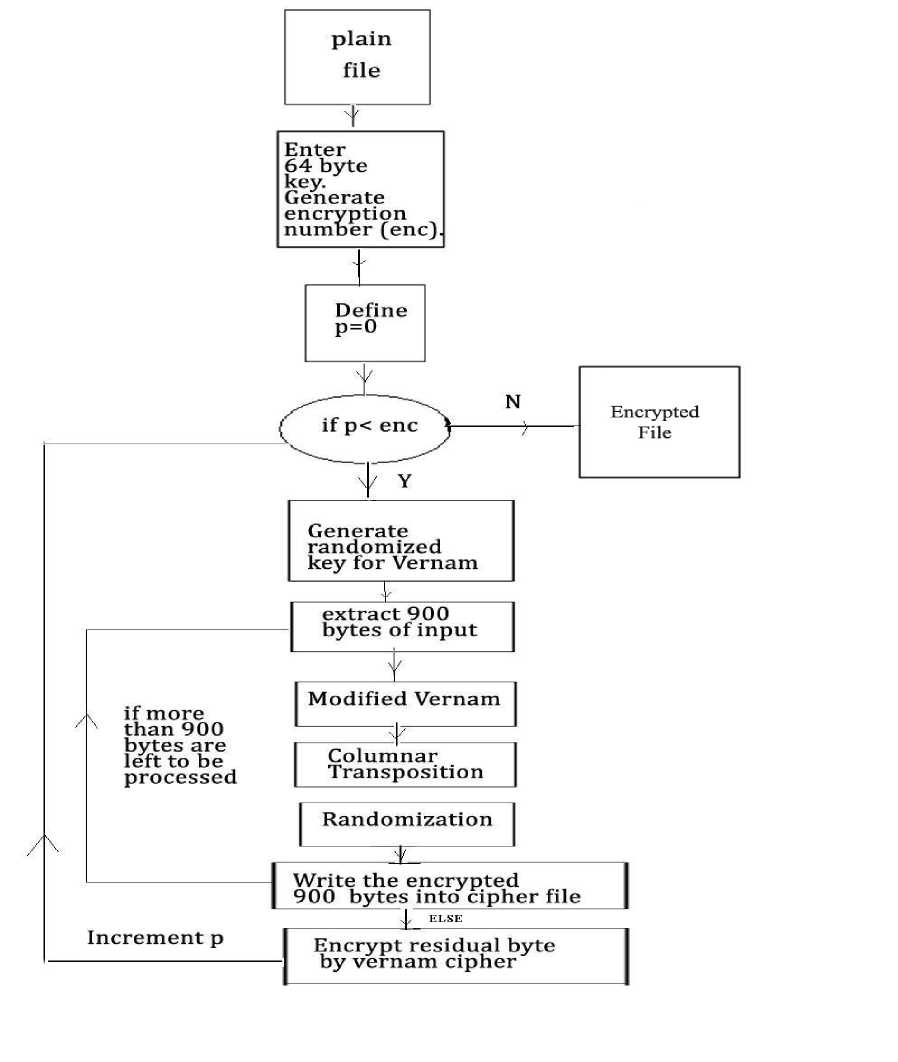
Figure-1: Diagrammatic Representation of Modified UES Version-I

• IV.    TEST RESULTS OF MODIFIED ULTRA ENCRYPTION METHOD VERSION-I

Table-III:

Plain Text	Cipher Text
he is great	e™,;5®T4@YS/
se is great	pIZKASuDn-Y
ie is great	oa'^-^ '%, <
Aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaa	hHY.ILoWkRv IN\eSi<\Ve-pT^/“3s-x-E2U?:DYl ^ jej °=B«aRZf?hQiE0Ol2Y;u ¸)~úW½Xî0ùÿÑb • Ä°údfâ\îPÙo"ÖÍ
The Indian Higher education System has established itself as one of the largest in the world in terms of the number and diversity of institutions and student enrolment. However the nature of demand for higher education in the 21st century is undoubtedly influenced by macro-economic trends like the changing composition and preferences of students, an increasing willingness to spend more on quality education, a greater demand for global education, employability linked education, rapid privatization and globalization.	~ 7K. ^' 6mO±aanAMH^IG'|O™# ^ DEJ>/°^ N'™ G.ai'alA vU' §e'a9“() iuK1 >vT)$“q [ 3K i b ^:9eAiZH3op\_+v„(O/UZ0/OaoZHTQ6yD'[p_^a_ilkj G-3® § ]Z_B®^Hsz"9_Uy$„ "Yaa j Y0I_N€6yAHX ¥¥ad<ёW„,A._/U0iu • %y8 ^&nWfMU0>1h%~ ¥ ]y2 ^Ew±b_V%oB4[^7®u@$s_цEY :BKKcC_eyG”°9^_^ • i !eU • л"_F="“~>UYYi:A^0@ц_ё^zj,RnY™б^SBЁ^_ };sa©iJsb$A%§uALq#6Au>j'IRi_™i%al0yZy6Oc_A‘~ b°jUuOG3E_'Y64йi|Oл_$LB|ё_xцPZ_ц_/C[H{a }@ "}uKa'rSZ0EAf«Zoxyq:auO\_Pu+MAIyUkJ#_}‘EOG \a iL'_1OxOl7aetc5ASi__2$a—™w^
Aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaaaab	0 RC'v1 .CR^Sqio.KRIBbB    ”|0(']#_фК1_- *_B@ )Oupn,©vh¥U__Ue * 1”=_^]$)агё~'©Ь°^?§ H_Ou’irё!_’14qu;•_"nUu_qVx.s'a_=„_^Ai&^nO_“Ё_9
AAAABBBAAAA	—D!wvW^^/_%O
AAA	—B!P
ABA	—N10
AAB	~aa ^
ABC	™nCX
AB	~a’
A	—©
B	™E

• V.    DISCUSSIONS ON TEST RESULTS

In Modified UES Version-I, we have implemented the three techniques of encryption with a great deal of flexibility. The addition of multiple encryption technique (minimum 7 times), the randomized Vernam key generation and finally the automatic column sequence in columnar transposition method makes this algorithm formidable. For almost same characters as input, the cipher file is completely different.

To illustrate our point consider the following example

Plain Text: he is good

Cipher Text: ZZ_umJY_E_

Plain Text: he is goon Cipher text: GjYu>A°

• VI.    CONCLUSION AND FUTURE SCOPE

In the present paper we have used three different cryptography algorithms in two distinct versions. In the Modified UES Version-I the authors have applied the three encryption methods empowered with multiple encryption, randomized key generation and sequence of column extraction on some known text where the same character repeats for a number of times and we have found that after encryption there is no repetition of pattern in the output file. At the outset the modified Vernam Cipher Encryption Technique with feedback encrypts the plain text file such that even the same characters are encrypted to different cipher characters. Then the Columnar Transposition and the Permutation/Randomization technique ensure that the cipher file becomes encrypted to a greater degree. There is lot of scope to modify the present method. The merit of this method is that it is almost impossible to break the encryption algorithm without knowing the exact key. We propose that this encryption method can be applied for data encryption and decryption in corporate sectors, academic institution etc. for sending confidential data.

ACKNOWLEDGEMENT

We are very much grateful to Department of Computer Science to give us opportunity to work on symmetric key Cryptography. One of the authors (AN) sincerely expresses his gratitude to Fr. Dr. Felix Raj and Fr. Jimmy Keepuram for giving constant inspiration to carry out research work. AN is grateful to the University Grants Commission for giving financial assistance through Minor Research Project. JN expresses her gratitude to A.K.School of IT for allowing us to work in research project at St. Xavier’s College. SR, NM, SA and AN are also thankful to all 3rd year Computer Science Hons. Students (2011-2012 batch) for their encouragement to finish this work.