Ультранизкочастотные волны в Космосе и на Земле

Все околоземное пространство заполнено ультранизкочастотными (УНЧ, ultralow-frequency – по западной терминологии) волнами. УНЧ волны занимают диапазон, покрывающий три порядка по частоте, от первых мГц до нескольких Герц. УНЧ волны проявляются в данных спутниковых и наземных магнитометров как геомагнитные пульсации, т. е. короткопе-риодные колебания магнитного поля. Верхняя частота диапазона геомагнитных пульсаций соответствует гирочастоте протонов в магнитосфере (~3–5 Гц), нижняя определяется основным периодом колебаний магнитосферной полости в целом (~доли мГц). УНЧ волны, пронизывающие все околоземное космическое пространство, доносят до земной поверхности информацию о свойствах окружающей Зем- лю плазмы [Walker, 1993; Guglielmi and Pokhotelov, 1996].

УНЧ пульсации геомагнитного поля были, по существу, первыми электромагнитными волнами, зарегистрированными человечеством с помощью простейших магнитометров. Энергетически УНЧ вол- ны являются самым мощным природным волновым электромагнитным процессом в околоземном пространстве, как видно из сравнения спектральной плотности различных типов природных излучений на рисунке 2.

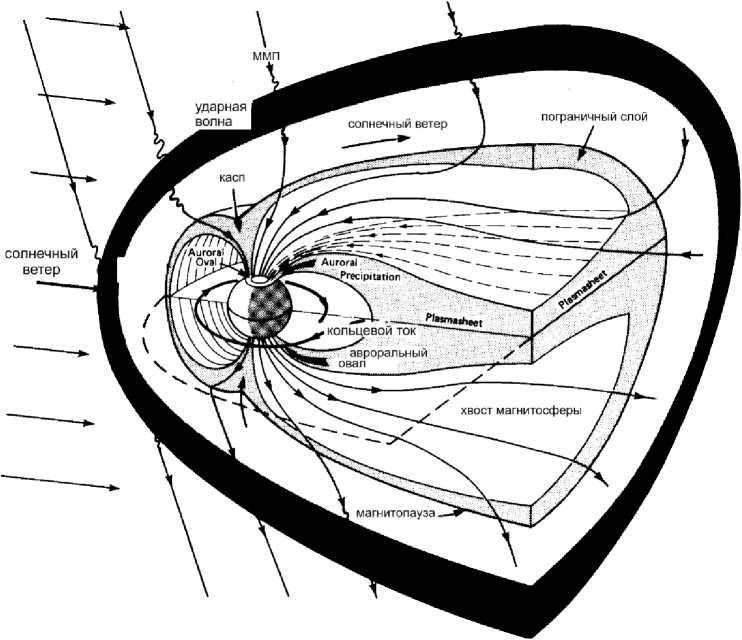
Рис. 1. Общая структура магнитосферы Земли

Здесь дан краткий обзор современных представлений о физической природе волновых вариаций геомагнитного поля в УНЧ диапазоне. Шумы и колебания УНЧ диапазона отражают турбулентный характер взаимодействия плазмы солнечного ветра с земной магнитосферой. Возбуждение некоторых типов УНЧ волн являются проявлением резонансного взаимодействия волн и частиц в околоземной плазме. Физика УНЧ волн опирается на теоретический аппарат физики плазмы и магнитной гидродинамики, а экспериментальной базой исследований являются данные наблюдений на спутниках и наземных станциях. Изложение рассчитано на чита- телей, работающих в смежных областях (космические технологии, геофизика), которые хотели бы получить общее представление о физике УНЧ волн в ближнем космосе. Поскольку данная работа – это не научный обзор для специалистов, а скорее введение в проблему для начинающих исследователей, то детальные ссылки опущены, а дается список монографий и обзоров, где можно найти информацию обо всех узкоспециальных работах. Сначала приведены морфологические характеристики основных типов геомагнитных пульсаций, а затем рассмотрены их физическая природа и механизмы генерации.

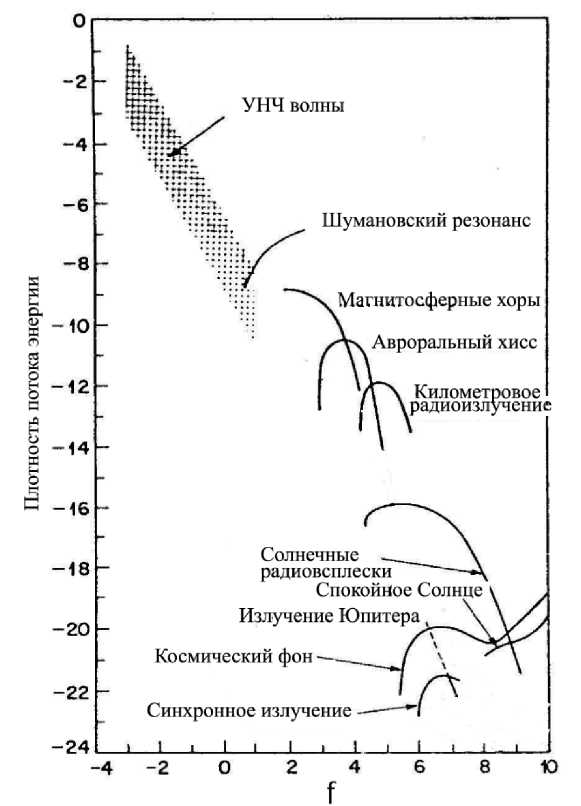
Рис. 2. Спектральные плотности мощности различных типов природных излучений в око- лоземном пространстве.

Морфологические свойства и классификация геомагнитных пульсаций

Геомагнитные пульсации разделяются на два больших класса [Троицкая и Гулье-льми, 1969]: непрерывные (Pc – pulsations continuous) пульсации от Рс1 до Рс5, которые характеризуются квазисинусоидаль-ной формой, и иррегулярные (Pi – pulsations irregular) пульсации от Pi1 до Pi3, имеющие вид отдельных всплесков или широкополосных вариаций. Как правило, непрерывные (Рс) пульсации характерны для дневного времени, а иррегулярные пульсации (Pi) – для ночного. Генерация пульсаций типа Pc определяется крупномасштабной динамикой околоземной плазмы и в большинстве случаев связана с взаимодействием солнечного ветра с магнитосферой. Иррегулярные пульсации типа Pi, как правило, связаны с развитием магнитосферных суббурь, при этом возбуждение колебаний происходит в локализованных областях ночной магнитосферы.

Основные типы геомагнитных пульсаций исторически классифицируются согласно диапазону частот/периодов, в котором они наблюдаются [Пудовкин и др., 1976]. Как правило, каждый тип пульсаций отличается от другого не только диапазоном периодов, но и физической природой возбуждения волн. Установленные классификацией границы периодов для того или иного типа пульсаций носят условный характер, т. к. параметры околоземной среды крайне динамичны. Характерная амплитуда геомагнитных пульсаций резко возрастает с увеличением их периодов: так, если амплитуда короткопериодных пульсаций (Pc1-2, Pi1) составляет сотые и десятые доли нТл, то амплитуда длинно- периодных пульсаций (Рс5, Pi3) может достигать нескольких сотен нТл.

Геомагнитные пульсации Рс5

Пульсации Рс5 (Т ~ 150–600 с, f ~ 1,5– 6,7 мГц) заполняют низкочастотную часть спектра УНЧ волн. В высоких широтах амплитуды Рс5 обычно составляют ~40– 100 нТл. Пульсации Рс5 являются, в ос- новном, высокоширотным явлением и типичны для восстановительной фазы суббури. На рисунке 3 показан пример регистрации Рс5 пульсаций в авроральных широтах. Колебания Рс4 диапазона (T~40– 150 c) как правило являются гармоникой Рс5 колебаний.

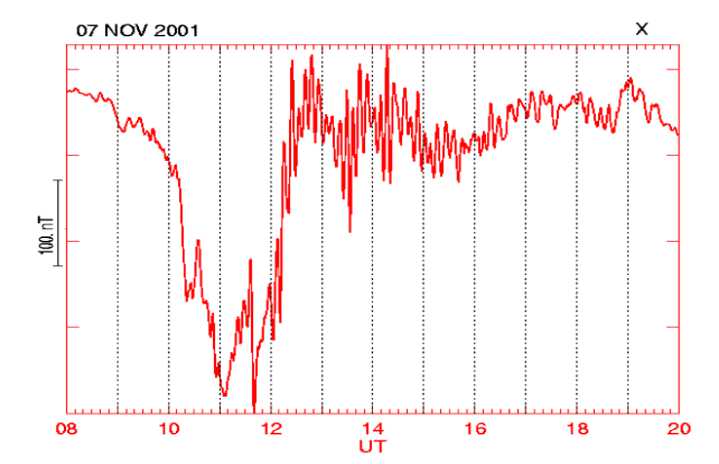
Рис. 3. Пример записи пульсаций Рс5 в авроральных широтах (Х-компонента)

Максимум амплитуды Рс5 наблюдается в авроральной зоне и смещается к более низким широтам при увеличении магнитной активности. В суточном ходе частоты появления пульсаций отмечается два максимума: основной – в утренние часы (07– 09 MLT), и второй, несколько меньший – в послеполуденные часы (15–17 MLT). Период наблюдаемых пульсаций возрастает с увеличением широты. Направление вращения вектора поляризации волн различно на широтах выше и ниже амплитудного максимума на данном меридиане.

Наблюдения Рс5 пульсаций на сети станций показывают специфическую пространственную картину. В долготном направлении на фиксированной широте колебания сдвинуты по времени. Этот временной сдвиг соответствует фазовой скорости, направленной в анти-солнечном направлении – на запад в утренние часы, и на восток – в вечерние. Изменение направления азимутальной скорости распространения совпадает с изменением направле- ния вращения вектора поляризации знак вблизи полудня. Азимутально распространение характеризуется безразмерным волновым числом m = Δφ/ ΔΛ , где □φ – фазовый сдвиг, ΔΛ – разнос станций по долготе. Типичные значения m~3–5. В широтном направлении вдоль меридиана пространственная структура неоднородна, и проявляет локальный максимум амплитуды. Фазовая картина поля волны неоднородна и демонстрирует резкое изменение хода фазы только вблизи максимума амплитуды. Фазовые сдвиги указывают кажущееся направление распространения к высоким широтам.

В сопряженных точках Рс5 пульсации наблюдаются одновременно, направление вращения горизонтального вектора волн в обоих полушариях совпадает, если смотреть в направлении геомагнитного поля.

В восстановительную фазу очень больших магнитных бурь при наличии высокоскоростных потоков солнечного ветра возможно возбуждение глобальных Рс5

пульсаций. В отличие от обычных Рс5 пульсаций, эти монохроматические колебания наблюдаются одновременно в огромной области геомагнитных широт от средних до приполярных околополуденно- го сектора (рис. 4). Амплитуда глобальных Рс5 пульсаций почти на порядок больше, чем амплитуда обычных Рс5 пульсаций и может достигать ~300–400 нТл.

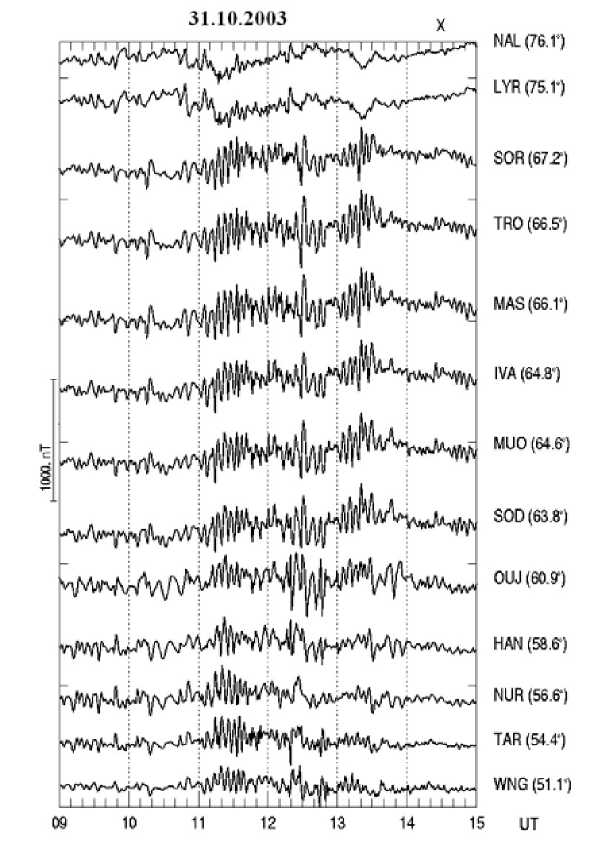
Рис. 4. Пример магнитограмм глобальных Рс5 пульсаций в послеполуденном секторе во время фазы восстановления большой магнитной бури.

Наблюдения на спутниках показали, что на больших расстояниях (>6R E , где R E – радиус Земли) пульсации диапазона Рс5 являются типичным явлением во внешних областях возмущенной магнитосферы. С наблюдательной точки зрения магнитосферные УНЧ волны в частотном диапазоне Pc4-5 можно разделить по их характерной поляризации на основные типы: тороидальные, компрессионные, полои-дальные. В свою очередь поляризация МГД волн тесно связана с их пространственной структурой.

• -    Тороидальные пульсации – крупномасштабные колебания геомагнитного поля с преобладающей поляризацией в азимутальном направлении, которые чаще всего наблюдаются на дневной стороне или на флангах магнитосферы. Для них характерны малые значения азимутального волнового числа m порядка первых единиц. Тороидальные пульсации вызываются источником на магнитопаузе или волнами, проникающими из солнечного ветра внутрь магнитосферы.

• -    Полоидальные пульсации являются азимутально-мелкомасштабными колебаниями с волновыми числами m>>1. Эта разновидность колебаний получила название storm-time Pc5 waves (рис. 5). Хотя амплитуда этих колебания велика (на геостационарной орбите достигает 1/3 от по-

• стоянного поля магнитосферы), на земле эти колебания не наблюдаются. Полои-дальные колебания черпают энергию локально внутри магнитосферы, от взаимодействия с энергичными заряженными частицами.

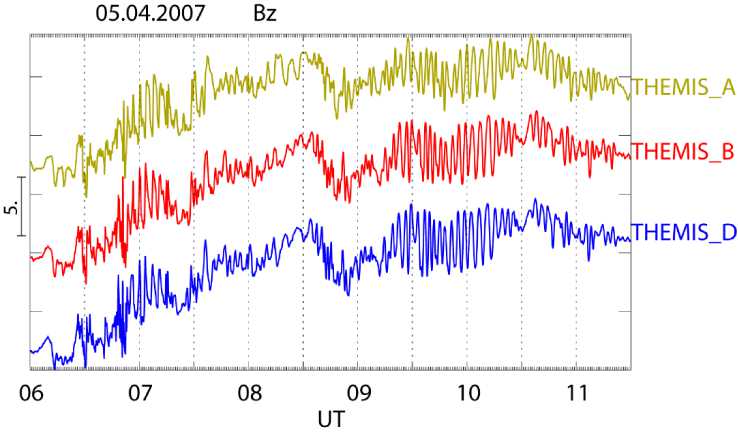
Рис. 5. Пример компрессионных колебаний диапазона Рс5 во время магнитной бури, зарегистрированных на спутниках THEMIS

• -    В структуре компрессионных колебаний преобладает компонента сжатия магнитного поля ^B . Как правило, компреси-онные колебания оказываются и полои-

• дальными, т. е. имеют малый азимутальный масштаб.

Модельная пространственная структура тороидальных и полоидальных пульсаций показана на рисунке 6.

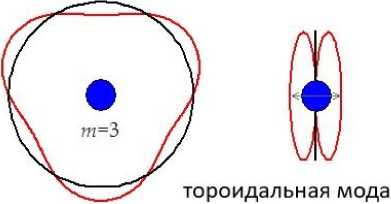
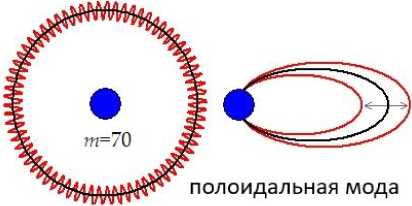
Рис. 6. Иллюстрация пространственной структуры тороидальных (малые азимутальные числа m ) и полоидальных (большие m ) колебаний

Геомагнитные пульсации Рс2-4

Геомагнитные пульсации этого диапазона (частоты от десятков до сотни мГц) являются самыми распространенными видами дневных колебаний, которые могут продолжаться часами и наиболее типичны для средних широт. Возбуждение этих видов геомагнитных пульсаций наблюдается от экваториальных областей до полярной шапки, при этом их амплитуда возрастает с ростом широты точки наблюдения. Так, амплитуда колебаний с периодом T~20– 30 с в средних широтах составляет десятые доли нТл, а в высоких – единицы и первые десятки нТл. В магнитосфере на спутниках геомагнитные пульсации диапазона РсЗ-4 также наблюдаются регулярно. Пример пульсаций Рс3, зарегистрированных на спутнике MMS, дан на рисунке 7.

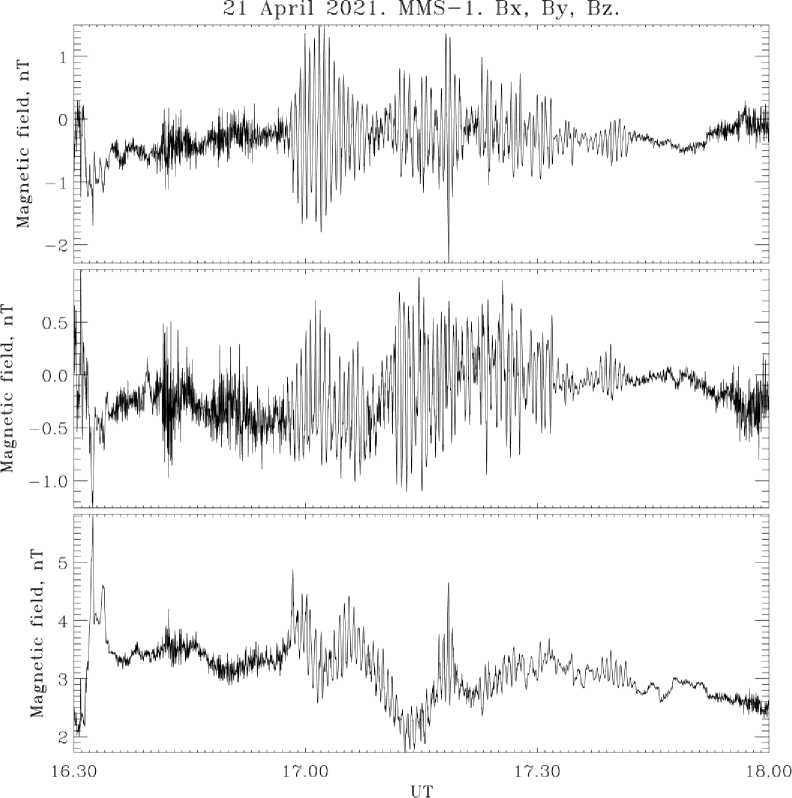
Рис. 7. Пример магнитограммы пульсаций Рс3 , зарегистрированных трехкомпонентным магнитометром спутника MMS

Пульсации Рс2-4 имеют, как правило, эллиптическую поляризацию с преобладанием левого вращения в дополуденное время и правого – в послеполуденное, что позволило предположить, что источник этих волн располагается на подсолнечном меридиане магнитосферы. В сопряженных точках Рс2-4 пульсации наблюдаются синхронно, направление вращений векторов синфазное в H-компоненте и противофазное в D-компоненте поля.

С ростом магнитной активности период Рс3 колебаний, регистрируемых в данной точке, уменьшается и сдвигается в диапазон Рс2, а при уменьшении магнитной активности – в диапазон Рс4. В широтном распределении амплитуд РсЗ пульсаций четко выделяется два максимума: средне- широтный (геомагнитные широты 55-60°) и высокоширотный (геомагнитные широты 70-74°) по обе стороны проекции плаз-мопаузы. Поляризация волн вблизи максимумов линейная, знак вращения вектора поляризации меняется на широте амплитудного максимума.

Характеристики Рс2-4 пульсаций тесно связаны с параеметрами турбулентной области перед фронтом ударной волны (форшок), где происходит возбуждение УНЧ волн (upstream waves) пучками отраженных протонов на фронте ударной волны. Частота возбуждаемых волн связана с величиной межпланетного магнитного поля (В) линейным соотношением: f [мГц]~6В [нТл]. Надежно установлен эффект модуляции интенсивности Рс3 пульсаций ориентацией межпланетного магнитного поля (ММП), а именно конусного угла □ □ – угла между направлением ММП и линией Земля-Солнце. Интенсивность пульсаций Рс3 резко усиливается при малых значениях конусного угла.

Геомагнитные пульсации Рс1

Геомагнитные пульсации Рс1 (диапазон частот от долей Гц до нескольких Гц) наблюдаются как в виде неструктурированного излучения, так и в виде структурированной последовательности квазимо-нохроматических волновых пакетов. Структурированные Рс1 получили поэтическое название «жемчужины» (pearls) за их характерную модуляцию амплитуды в виде отдельных цугов длительностью 14 мин., повторяющихся через 1-2 мин., и наблюдающихся непрерывными сериями длительностью от нескольких минут до нескольких часов. Колебания могут одновременно регистрироваться в большом диапазоне долгот (до 120˚) и несколько сотен км по широте. Пример магнитограммы и спектрограммы Рс1 пульсаций «жемчужин» показан на рисунке 8.

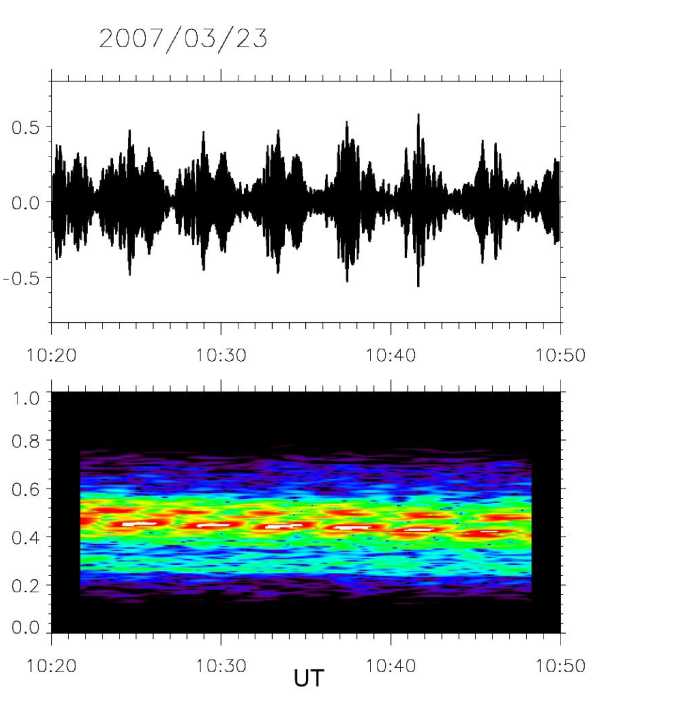
Рис. 8. Магнитограммы (вверху) и динамический спектр (внизу) структурированных Рс1 пульсаций (жемчужин)

Пульсации Pc1 «жемчужины» характерны для утренних и дневных часов местного времени и восстановительной фазы магнитной бури, когда происходит заполнение плазмосферы холодной плазмой, а в главную фазу магнитной бури они появляются крайне редко. «Жемчужины» Рс1, в отличие от всех остальных типов пульсаций, наблюдаются в геомагнитно сопряженных точках не одновременно, а попеременно, т. е. Рс1 волновые пакеты в магнитосфере распространяются из одного полушария в другое вдоль силовых линий геомагнитного поля. Динамические спектры «жемчужин» Pc1 являются результатом дисперсии групповых скоростей при распространении волновых пакетов Рс1 волн между точками отражения в противоположных полушариях и представляют собой серии дискретных тонов с возраста- ющей частотой и наклоном структурных элементов. По данным наблюдений на наземных обсерваториях и на низкоорбитальных спутниках, максимум появления Рс1 отмечается на широтах, соответствующих наиболее вероятному положению плазмопаузы (геомагнитные широты 58°– 61°).

Подклассом Рс1 пульсаций являются колебания с убывающим периодом (КУП) или IPDP (irregular pulsations with diminishing period ) , которые на земной поверхности наиболее часто наблюдаются в послеполуденном и вечернем секторах в возмущенных условиях. На магнитограммах они видны как серии отдельных цугов, подобных колебаниям Pс1 , но с монотонно увеличивающейся частотой от долей Гц до нескольких Гц (рис. 9, верхняя панель).

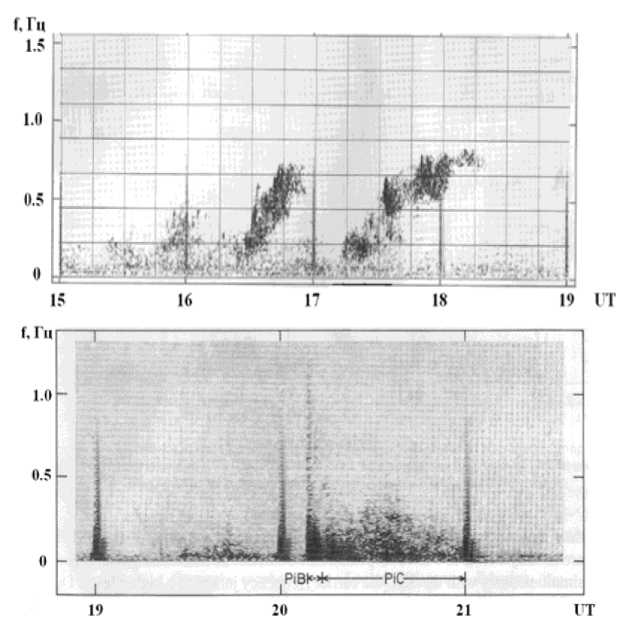
Рис. 9. Динамические спектры геомагнитных пульсаций КУП (вверху) и геомагнитных пульсаций PiB и PiC (внизу).

Чем сильнее магнитная буря, тем вероятнее возбуждение IPDP и тем круче нарастает частота колебаний. Другим важным отличием IPDP пульсаций от «жемчужин» является их синхронное появление в сопряженных точках. Генерация КУП наблюдается на фоне интенсивных магнитосферных суббурь и усиления кольцевого тока.

Иррегулярные геомагнитные пульсации Pi

Иррегулярные пульсации являются атрибутом возмущенной магнитосферы, и они тесно связано с развитием магнитосферных суббурь. Генерация различных типов таких пульсаций происходит в определенной последовательности на разных этапах магнитосферной суббури и отражает характерную перестройку структуры ночной магнитосферы.

Короткопериодные иррегулярные пульсации ( Рi1 ) с T<40 с разделяются на два типа: широкополосные импульсные ( РiВ ) и шумовые ( РiС ) в конечной частотной полосе (T~5–10 с). В возмущенных условиях оба типа пульсаций могут регистрироваться одновременно. Пример динамического спектра этих пульсаций приведен на рисунке 9 (нижняя панель).

РiВ пульсации на магнитограммах имеют вид шумовых всплесков длительностью ~1-3 мин. РiВ пульсации наблюдаются в вечерние и ночные часы местного времени и сопровождаются локальным высыпанием энергичных электронов, уяр-чением дискретных форм полярных сияний и локальным усилением вытекающих продольных токов. Наибольшие амплитуды этих колебаний регистрируются в авроральных широтах и типичны для взрывного начала суббури. Они могут использоваться для точного определения времени начала суббури и суббуревых интенсификаций.

РiC пульсации представляют собой иррегулярные колебания в ограниченной полосе частот 0,01-0,2 Гц. Такие колебания обычно наблюдаются во время суббури в утреннем секторе экваториальной границы авроральной зоны и сопровождаются пульсирующими пятнами диффузных сияний и пульсирующим риометрическим поглощением.

Геомагнитные пульсации Pi2-3

Во время геомагнитной суббури в ночном секторе магнитосферы и ионосферы разыгрываются целый комплекс волновых процессов. Неотъемлемым элементом суббури являются Pi2 геомагнитные пульсации (T~50–150 с), представляющие собой цуг затухающих колебаний длительностью порядка нескольких периодов [Keiling and Takahashi, 2011]. На земной поверхности эти глобальные пульсации наблюдаются на всех широтах, от экватора до ночной стороны полярной шапки. На низких широтах Pi2 регистрируются на всех долготах, включая даже дневную сторону, в средних и высоких широтах они отмечаются наиболее часто в ночном секторе. Амплитуда Pi2 пульсаций возрастает с широтой, на низких широтах она составляет единицы и даже десятые доли нТл, а в авроральной зоне может достигать значений ~100 нТл.

Одним из важнейших свойств Pi2 пульсаций, часто используемым при изучении процессов в авроральных широтах, является их четкая связь с взрывной фазой магнитосферной суббури, поэтому всплески Pi2 пульсаций (особенно в средних широтах) используются как простой и надежный индикатор начала магнитосферной суббури. При этом возбуждение цуга Pi2 в авроральных широтах обычно сопровождается всплеском колебаний PiB . Возбуждение Pi2 сопровождается интенсификацией полярных сияний, усилением ионосферных и продольных токов, высыпанием энергичных электронов и другими процессами.

Пульсации в диапазоне Pi2 уверенно регистрируются на высокоэллиптичных, геостационарных, и низкоорбитальных спутниках. Во внутренней магнитосфере характерной чертой волн в диапазоне Рi2 является преобладание продольной составляющей. Пример синхронной регистрации Pi2 пульсаций на сети низкоширотных наземных станций и на низкоорбитальном спутнике приведен на рисунке 10.

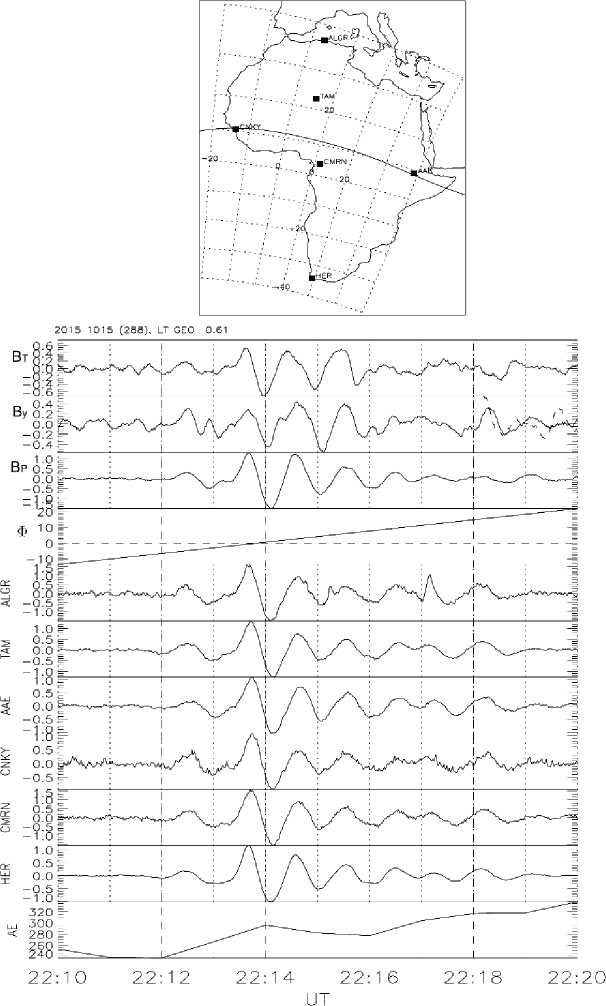
Рис. 10. Пример одновременных Pi2 пульсаций на станциях наземной сети AMBER (Африка) и на низкоорбитальном спутнике SWARM (положение станций и проекция орбиты показаны на отдельной вставке). Верхние три панели – магнитограммы компонент B T , B y , B p на спутнике, 4-я панель – географическая широта спутника Φ , следующие шесть панелей – магнитограммы наземных станций, нижняя панель – индекс авроральной активности АЕ

На фоне суббури часто наблюдаются длиннопериодные иррегулярные пульсации Pi3 (или Ps6) с T~10–20 минут. Эти пульсации являются тонкой структурой суббури, и представляют собой квазипе-риодическую последовательность импульсов с амплитудами до нескольких сотен нТл (рис. 11).

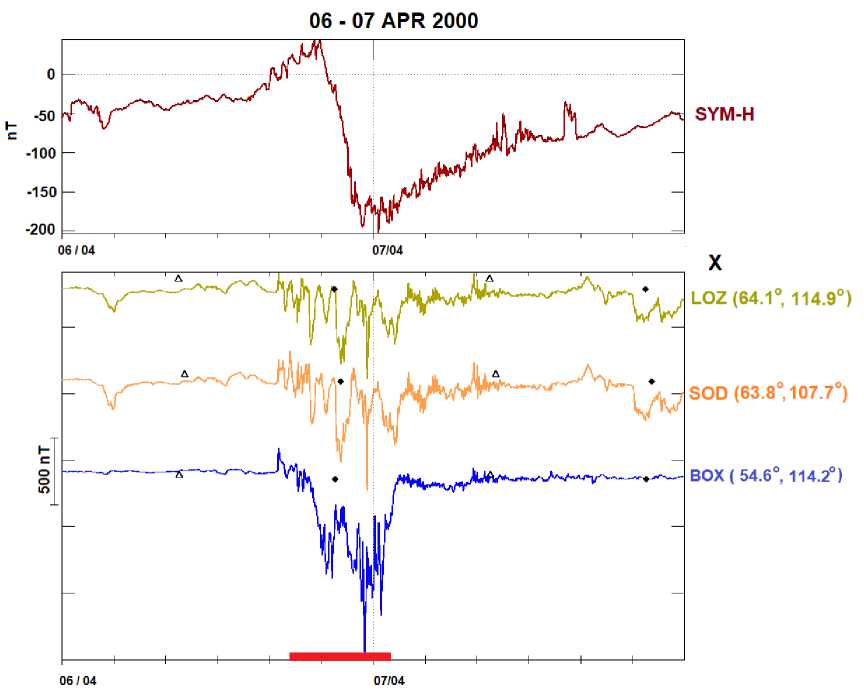
Рис. 11. Пример суббури с одновременными Pi3 пульсациями (Х-компонента). Верхняя панель показывает вариации SYM-H индекса, характеризующего интенсивность магнитной бури. Красная черта указывает период времени с аномалиями в работе систем железнодорожной сигнализации.

Длиннопериодные волны в дневной пограничной области

Дневная высокоширотная область характеризуется увеличенной УНЧ активностью, включающей длиннопериодные ква-зипериодические вариации и Pc5 волны. Нерегулярные низкочастотные (T~доли мГц) пульсации наблюдаются почти каждый день, когда наземная обсерватория оказывается в пределах нескольких часов от местного полудня (рис. 12). Эти высокоширотные квазипериодические возмущения получили название IPCL (Irregular Pulsations at Cusp Latitudes). Ранние исследования дневной УНЧ-активности в высоких широтах давали надежду, что эти длиннопериодные нерегулярные вариации могут быть использованы в качестве простого индикатора положения дневного каспа и границы полярной шапки. Предположительно, граница замкнутых и открытых силовых линий должна проявлять- ся в переходе от колебаний Pc5 к IPCL колебаниям с большим периодом.

Однако связь дневных высокоширотных УНЧ флуктуаций с каспом или границей замкнутых силовых линий все еще остается под вопросом. Хотя повышенные уровни УНЧ активности действительно наблюдаются в области около каспа, сам касп может не быть источником активности, наблюдаемой на земле. Механизм неустойчивости сдвигового потока, такой как неустойчивость Кельвина-Гельмгольца, ответственный за возбуждение утренних Pc5 пульсаций, вряд ли может работать в околополуденные часы, где поток обтекающей магнитосферу плазмы солнечного ветра довольно медленный. Спорадические нерегулярные пульсации в области каспа могут быть вызваны динамическими явлениями в солнечном ветре: скачками давления, импульсным пересо-единением на магнитопаузе (Flux Transfer

Events), аномалиями горячего потока (Hot турбулентности магнитослоя. Flow Anomalies), перемежаемостью МГД

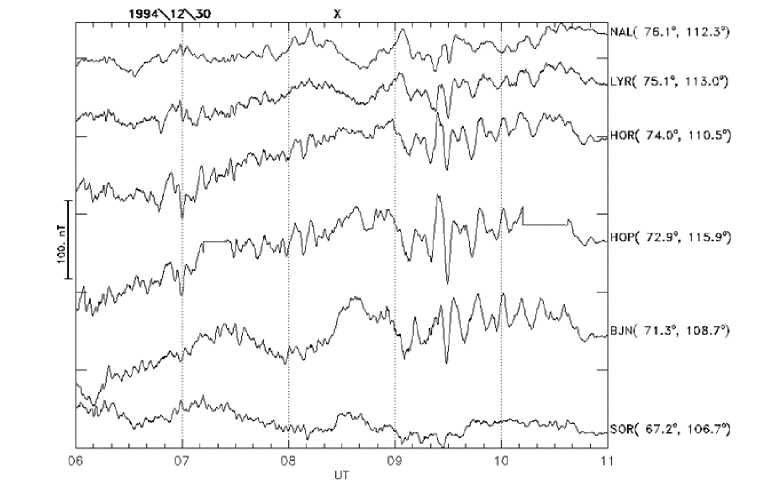
Рис. 12. Пример IPCL пульсаций на высокоширотных станциях сети IMAGE. Местный полдень соответствует 09 UT.

Вероятно, что дневные квазимонохро-матические Pc5 и широкополосные IPCL пульсации не являются отдельными явлениями, а являются проявлениями одного и того же процесса возбуждения, в то время как разница в их появлении связана с различием в магнитосферном отклике. Также кажется возможным связать низкочастотные IPCL с поверхностными модами магнитопаузы. Тогда наиболее интенсивный наземный отклик на колебания магнитопаузы следует ожидать под ионосферной проекцией границы замкнутых силовых линий.

До сих пор пространственное соответствие между дневными пограничными областями и наземной УНЧ активностью надежно не установлено. Чтобы однозначно определить связь дневной высокоширотной УНЧ активности с дневным каспом могут быть использованы потенциальные возможности меридиональных сканирующих фотометров и магнитометрических цепочек станций вдоль геомагнитной долготы. Непосредственно к экватору от области высыпания мягких частиц каспа расположена граница открытых/закрытых силовых линий. Оптические признаки высыпания электронов легко распознается по наличию красного сияния, т. к. касп – единственная область, где частицы солнечного ветра из магнитослоя имеют прямой доступ к ионосфере. Также ионосферные проекции различных областей дневной магнитосферы могут быть определены с помощью ВЧ радаров SuperDARN путем изучения спектральной ширины рассеянного сигнала, и по измерениям частиц на низкоорбитальных космических аппаратах типа DMSP и NOAA.

Физические механизмы УНЧ волн МГД колебания (пульсации Рс3-5) Хотя исследование плазменных и электромагнитных волновых явлений в околоземном пространстве опирается на математический аппарат и теоретические подходы, разработанные в физике плазмы и магнитной гидродинамике, нельзя сказать, что космическая геофизика занимается только приложением физических представлений, выработанных в общей физике плазмы. Ряд принципиально новых физических идей, получивших затем широкое развитие, взят физиками из космической геофизики: пересоединение силовых линий и аннигиляция магнитных полей, бесстолкновительные ударные волны [Solar Wind Sources of Magnetospheric Ultra-Low-

Frequency Waves, 1994]. Сюда же следует добавить и введенные Альвеном представления о магнитной гидродинамике и МГД волнах, отмеченные Нобелевской премией [ Pilipenko , 1990]. Эти волны диапазона от первых единиц до сотни мГц регистрируются спутниковыми и наземными магнитометрами в виде Рс3-5 пульсаций геомагнитного поля [ Гульельми и Троицкая , 1973]. Конверсия МГД волн в области аль-веновского резонанса, впервые предложенная для интерпретации структуры Рс3-5 волн в магнитосфере Земли, ныне широко используется в работах по управляемому термоядерному синтезу для радиочастотного нагрева плазмы.

МГД описывает крупномасштабную динамику плазмы как медленные движения проводящей жидкости и основана на самосогласованной системе уравнений гидродинамики, дополненных уравнениями Максвелла. Масштабы МГД возмущений должны превышать характкрный кинетический масштаб – ионный ларморовский радиус р = uj / О, (где ui - тепловая скорость ионов), а характерные частоты быть много меньше частоты циклотронного вращения ионов (ыП Ц). Эти параметры можно оценить по соотношениям Ц.[sec’1]^ 0.1 B[nT] , р [m]= 4.6 • 1067w[keVj/B[nT], u. [m/s]=4.4 • 105 7W[keV], W – энергия частицы. При таких низких частотах проводимость плазмы вдоль внешнего магнитного поля B0 очень велика, что позволяет считать продольное электрическое поле отсутствующим E ^ 0, а силовые линии – эквипотенциальными. При этом в отсутствие столкновений движения не слишком горячей плазмы и магнитных силовых линий как бы вморожены друг в друга, E± + [V x Bq ] = 0, т. е. поперечное электрическое поле E неразрывно связано со скоростью движения плазмы V.

В холодной плазме, где отношение теплового и магнитного давлений ^в = 2 ^ 0 P / B 0 <<¹, могут распространяться два типа МГД волн – быстрые магнитозвуковые (БМЗ) и альвеновские. БМЗ волны аналогичны обычным звуковым волнам, только возмущение в них передается не сжатием газа, а сжатием магнитного поля, и роль газового давления P играет давление магнитного поля B 2 /2 p o . Как и акустические волны, БМЗ распространяется практически изотропно. Дисперсионное уравнение для БМЗ в наиболее важном для ситуации в околоземной плазме пределе, когда поперечный масштаб волны много меньше ее продольного масштаба k _± >>  k , имеет вид:

Здесь V_A = В _о / 7 ^р - альвеновская скорость, которую можно оценить по соотношению V _A[km/s] = 22 B [nT]/7 N [cm^-3] , k = k_z и k - волновой вектор вдоль и поперек В 0 .

В плазме конечного давления ( р ~1) возникает мода медленного магнитного звука (ММЗ). В том же пределе k_± >>  к дисперсионное уравнение для ММЗ имеет вид:

ы = kV

Здесь Vs = 7Te / Mi - ионно-звуковая скорость, определяемая температурой электронов Te и массой ионов Mi. ММЗ напоминает колебания воздуха внутри труб органа, и энергия ММЗ распростра- няется практически вдоль силовой линии. БМЗ и ММЗ моды являются компрессионными, т. е. сопровождаются возмущением величины магнитного поля. При этом у БМЗ магнитное и плазменное давление осциллируют в фазе, а у ММЗ – в проти- вофазе. Таким образом, ММЗ волны обладают свойством диамагнитности.

Если БМЗ и ММЗ волны во многом аналогичны акустическим волнам в газе, то альвеновские волны принципиально отличаются от обычных волновых процессов в оптике, акустике или сейсмологии. Специфика магнитосферы как колебательной системы заключается в наличии в спектре ее собственных колебаний частотных интервалов, соответствующих альвеновским колебаниям (альвеновскому континууму) [ Alperovich and Fedorov, 2007 ]. Наглядно альвеновский континуум можно представлять как арфу с набором непрерывно изменяющихся струн. Их спектр даже в ограниченной системе непрерывен, а собственные функции сингулярны. Альвенов-ские волны обладают и другими интересными особенностями – одномерному характеру распространения вдоль поля В 0 и отсутствию геометрического затухания, возможности переноса нестационарного продольного тока вдоль силовых линий, отсутствию незатухающих решений даже в бездиссипативной системе, необратимой конверсии БМЗ возмущений в альвенов-ские волны в неоднородной среде.

В МГД возмущениях продольная компонента электрического поля пренебрежимо мала E_ ^ 0 из-за высокой проводимости плазмы вдоль внешнего магнитного поля. Поперечное к полю B = B e ( e z – единичный вектор вдоль внешнего поля) 2D электрическое поле ^E ⊥ МГД волны можно представить как сумму потенциальной и вихревой компонент Е± =—^Ф + [Vi ^x e_z ] Т,             где

V_± = ( д^ , д ) - поперечный Лапласиан.

( д 2 - V - д 2 ) E x ( t ,z) = ^ 0 д j ⁾( t , z )

В правой части фигурирует ток внешнего драйвера Лe ) , возбуждающего альве-новскую волну. Магнитная компонента поля альвеновской волны поперечна по

Потенциалы Φ и Ψ характеризуют поле альвеновской и БМЗ мод.

БМЗ волна, подобно звуковым волнам, стремится накапливаться в области с минимумом фазовой скорости. Таким области с минимумом альвеновской скорости оказываются естественными волноводами для БМЗ волн. В неоднородной по Х плазме, для БМЗ волны возникает точка отражение (поворота), в которой эффективное волновое число k² ( x ) = ш² / V² ( x ) - к² - k² обращается в 0. Областью прозрачности для БМЗ волны является область, ω ^> ω M , где ^ш М =^{( к} У ^{+ k} Z) V ^^{2( x} ). В БМЗ моде поперечная магнитная компонента безвихревая, [V_± x B_± ] = 0 , и отсутствует продольный ток j_z = 0 .

В альвеновской волне поперечные компоненты электрического и магнитные полей характеризуются потенциалом , т. е. E = -V_xФ и д t B = c [ e _z xV_±]д z Ф . Альве-новская волна переносит поперечный j ⊥ и продольный j токи, которые определяются соотношениями j i = ^ _AV A '^д t E ₁ и ^j z = ^ a ^V 1 ^Ф , где ^ a = 1/ M o ^v a - волновая альвеновская              проводимость,

V_A = B ₀ / 4^ ₀ Р — альвеновская скорость, □ – плотность плазмы. В однородной плазме дисперсионное уравнение для альвенов-ской волны имеет вид ω ⁼ ω A ^{≡ k} z ^V A . Характерное волновое число альвеновской волны к_А = ш / V_A . Электрическое поле альвеновского возмущения E , распространяющегося в однородной плазме вдоль магнитного поля, описывается волновым уравнением:

отношению к В 0 и бездивергентна V _±В_± = 0 , при этом продольная компонента исчезает B_z = 0 .

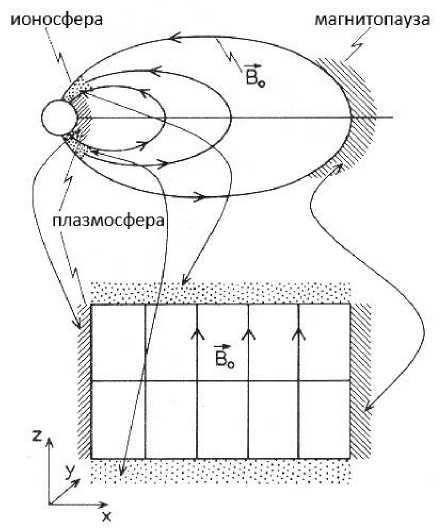
Рис. 13. Модель «плазменного ящика», моделирующая магнитосферный альвеновский резонатор, который образуется силовыми линиями геомагнитного поля, ограниченными сопряженными ионосферами ( z = ± L ). Прямые силовые линии направлены по оси Z, а радиальная неоднородность альвеновской скорости по оси Х моделируется неоднородностью плотности плазмы ^{р (} x ) . В направлении Y система однородна

Альвеновская волна, в отличие от БМЗ, не имеет точки отражения. Однако частичное отражение может происходить на границе плазменной системы (ионосфере) или от резких градиентов альвеновской скорости, что приводит к образованию альвеновских резонаторов. Основные представления о магнитосферном альве-новском резонаторе, который образуется силовыми линиями геомагнитного поля, ограниченными сопряженными ионосферами (z = ±L), были первоначально сформулированы в рамках одномерной модели т. н. «плазменного ящика» (рис. 13). В этой модели прямые силовые линии направлены по оси Z, а радиальная неоднородность альвеновской скорости по оси Х моделируется неоднородностью плотно- d2bz _ (kА)’ дbz । dx2 к 2Л - k 2Z дx сти плазмы Р( x). В направлении Y, соответствующем азимутальному направлению в магнитосфере, система однородна. В рамках модели плазменного ящика альве-новский континуум образуется непрерывным спектром мод магнитосферного резонатора с фундаментальным периодом T. (x ) = 4 L / Va (x).

В неоднородной плазме альвеновские и БМЗ волны не могут распространяться независимо друг от друга, а оказываются связанными. Для пространственновременной гармоники вида ^exp(- i ^ t + ik y y + ^ik z z) структура поля связанных БМЗ и альвеновских колебаний описывается уравнением:

A - k y - k z ²) = 0                               (4)

Неоднородность системы проявляется в наличии члена с (kЛ)'=дхk2(x) . Уравнение (4) имеет две характерных точки: син- гулярность в точке альвеновского резонанса kA = kz; и точку поворота для БМЗ волны kЛ (x) - kЛ - kz2 =0 . Сингулярный ха- рактер поля МГД волны в области альве-новского резонанса, полученный в модели плазменного ящика, сохраняется и в плазменных конфигурациях с многомерной неоднородностью [Alperovich and Fedorov, 2007]. Сингулярный характер решения волновых МГД уравнений в неоднородной среде указывает на возможность усиления волны в области альвеновского резонанса a = о, (x). Математическое описание структуры поля в окрестности резонансной оболочки в криволинейном поле можно получить в виде асимптотики:

B y (x , f ) = b o ( f) к ф

z ’’ +

h

C ln( im — z ) + ...

V .

B x (x , f ) = b o ( f) hi

hh im — ln( im — z) + hh

h

где z = x - ^x a ^{( f} ) + i S m , где x A ^{( f} ) — координата резонансной силовой линии; ^S _m – полуширина резонансной области. Метрические коэффициенты ^{( h} x , h, ) определяются выбором геометрии магнитного поля. Выражения (5) справедливы для самой общей геометрии магнитного поля и обобщают результаты более простой модели плазменного ящика. Например, коэффициент C 1 =0 в геометрии с прямыми силовыми линиями или с постоянной кривизной силовых линий. Принципиальной особенностью разложения (5) является наличие сингулярного члена 1/z в компоненте B y , ответственного за частотнозависимое усиление поля волны на резонансной оболочке ^x a ^{( f} ).

Качественно решение (5) может быть интерпретировано следующим образом. МГД возмущения БМЗ типа из внешней

Главный член асимптотического разложения (5), описывающий амплитудные и фазовые характеристики By составляющей области магнитосферы в процессе распространения вглубь неоднородной магнитосферы трансформируются в альвеновские колебания. Наиболее эффективно процесс трансформации колебаний происходит в окрестности резонансной силовой оболочки, где частота внешнего источника го совпадает c локальной частотой го а собственных колебаний геомагнитной силовой линии, т. е. а ^ о (x). В общем случае период колебаний силовой линии определяется собственными значениями 1D волновых уравнений вдоль силовой линии. В приближении геометрической оптики период альвеновских колебаний можно оценить как время пробега возмущения с аль-веновской скоростью между сопряженными ионосферами противоположных полушарий:

+ L

T A = / v ;'( s ) ds                              (6)

—L поля пульсаций в окрестности резонансной оболочки имеет вид:

B y ( x , f ) = b o ( f )

iS

m

Из-за диссипации в системе собственные частоты имеют мнимую добавку: ^a A ^ ^a A ^{- Y} . Декремент затухания У > ⁰

связан с шириной резонанса m над ионосферой соотношением Sm =Y(dxоА )-1. Исходя из (7) можно качественно предста- вить меридиональную структуру поля колебаний в виде суперпозиции сигнала «источника» bo(f) и резонансного отклика магнитосферного альвеновского резонатора, т. е. i^m /[x- xa (f) + i^m] (рис. 14). Сигнал «источника» обусловлен возмущением, переносимым крупномасштабной БМЗ волной, и слабо зависит от координаты. Резонансный же отклик магнитосферного резонатора, связанный с возбуждением альвеновских колебаний, сильно локали- зован и вызывает резкое изменение хода амплитуды и фазы пульсаций при переходе через резонансную оболочку. Компонента Bx поля пульсаций имеет более слабую (логарифмическую) особенность в окрестности резонансной оболочки, и резонансные эффекты в ее структуре проявляются слабо. Компонента сжатия (com-pressional) магнитного поля BZ регулярна в точке x=xA и имеет в ее окрестности малую, но конечную величину.

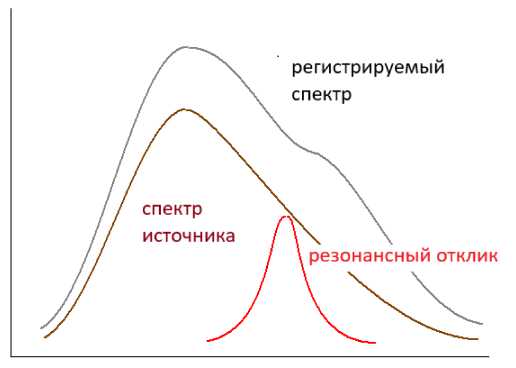
Рис. 14. Качественная иллюстрация меридиональной структуры поля пульсаций в виде суперпозиции сигнала «источника» и резонансного отклика магнитосферного альвенов-ского резонатора

Фаза возбуждаемого альвеновского возмущения испытывает скачок на при переходе через резонансную область. При этом знак скачка фазы определяется знаком радиального градиента альвеновской частоты ^д х ^ а . Обычно в магнитосфере (за исключением узкой области вблизи плаз-мопаузы) частота уменьшается с ростом широты, т. е. ^д х ^ а <  ⁰ . При этом соответствующая кажущаяся фазовая скорость колебаний направлена к периферии магнитосферы, т. е. к источнику колебаний. Качественно, такое поведение фазы можно объяснить тем, что возмущение из экваториальной плоскости магнитосферы доходит до ионосферы вдоль более коротких силовых линий на низких широтах быстрее, чем вдоль более длинных на более высоких широтах.

Широтный профиль фундаментального периода магнитосферного альвеновского резонатора, т. е. зависимость TA (L) от нормированного радиального расстояния L=r/RE (Re – радиус Земли), показан на рис. 15. Рассчитанный профиль показывает, что в принципе возможно образование трех областей с резонансным откликом на внешнее возмущение – внутри плазмосферы, на плазмопаузе, и вне плазмосферы (plasmatrough). Однако при детальном анализе широтного распределения Pc3-5 пульсаций были надежно выявлены субавроральный и среднеширотный максимумы, которые обусловлены магнитосферными резонансными эффектами в области вне плазмосферы и в плазмосфере, в то время как максимум на плазмопаузе либо не выделялся, либо был весьма слабым. Причина такого кажущегося парадокса, в том, что «каноническое» распределение TA(L) с резким падением на плазмопаузе на самом деле достаточно редкое событие и для его формирования требуется очень резкое па- дение плотности магнитосферной плазмы с расстоянием: N(r) ж LS, где s>8! В результате профиль TA(L) лишь выполажива-ется в районе плазмопаузы, и резонансный пик размывается и становится слабо заметным. Таким образом, при типичной структуре магнитосферы благодаря резонансному частотно-зависимому усилению интенсивные гармонические колебания диапазона Рс5 будут наблюдаться в субавроральной области, а Рс3 пульсации – на средних широтах.

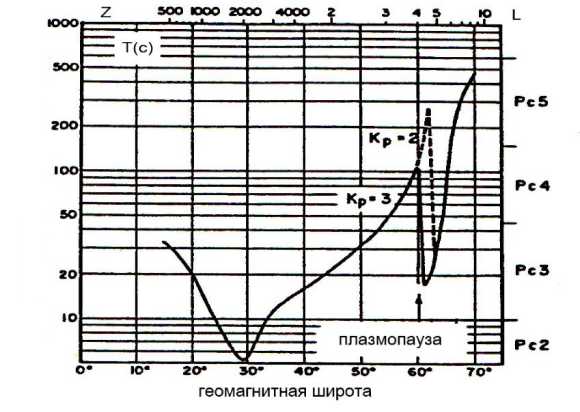
Рис. 15. Вычисленный широтный профиль фундаментального периода магнитосферного альвеновского резонатора, т. е. зависимость периода собственных тороидальных колебаний T A ( L ) от нормированного радиального расстояния L =r/R E или высоты z . Вертикальная

стрелка – положение плазмопаузы

Качественно новые особенности магнитосферного альвеновского резонатора начинают проявляться на низких геомагнитных широтах (ниже 30^о), где значительная часть силовой линии оказывается погруженной в ионосферную плазму с тяжелыми ионами. «Нагружение» силовых линий тяжелыми ионосферными ионами приводит к: (а) резкому увеличению декремента затухания Рс3 колебаний по мере приближения к экваториальным широтам, и (б) аномальной зависимости резонансного периода Т_А ( Ф ) - росту с уменьшением геомагнитной широты Φ за счет нагружения колеблющихся силовых линий тяжелыми ионосферными ионами. Искажение пространственной структуры поля в резонансной области при прохождении через ионосферу к земной поверхности рассмотрено в последующих разделах.

Объемные и поверхностные моды МГД колебаний

Объемная мода (cavity mode) образуется БМЗ модой, захваченной между магнитопаузой и плазмопаузой или Землей. Часто- та волноводных мод определяется условием квантования в радиальном направлении kXLX~ n, где LX – радиальный масштаб магнитосферного волновода. Оценка основной четвертьволновой моды T~4LX/VA соответствует частоте порядка первых мГц, если предполагать LX~5 RE и VA~800 км/с. В азимутальном направлении распределение плазмы не имеет резких градиентов, и волна может свободно распространяться в ночную магнитосферу. Таким образом, объемная волна является по существу модой магнитосферного проточного волновода.

В околоземной среде присутствуют области плазмы с резкими разрывами на границе раздела, например – магнитопауза и плазмопауза. На этих границах могут возбуждаться поверхностные волны, которые играют важную роль в передаче энергии и импульса внутрь магнитосферы. На дневной магнитопаузе, где скорость потока обтекающей магнитосферу плазмы мала, конечная протяженность силовых линий магнитосферы приводит к образованию поверхностной моды с дискретными частотами. На утреннем и вечернем флангах скорость обтекающей магнитосферу потока солнечного ветра велика, и магнитопауза может стать неустойчивой относительно возбуждения поверхностных колебаний результате неустойчивости Кельвина-Гельмгольца. Экспоненциальные «хвосты» крупномасштабных поверхностных волн выходят за пределы пограничного слоя и могут охватывать значительную часть плазменной конфигурации. Поверхностные волны на магнитопаузе могут порождаться при воздействии турбулентной плазмы магнитослоя или при импульсном широкополосном воздействии межпланетной ударной волной.

В реалистичной неоднородной магнитосфере глобальные поверхностные волны или объемные волны с дискретным спектром неизбежно должны быть связаны с альвеновским континуумом из-за резонансного межмодового зацепления на магнитной оболочке, где частота объем-ной/поверхностной моды совпадает с локальной частотой собственных колебаний силовой линии. В целом, как схематично показано на рисунке 16, магнитосфера оказывается подобной гигантскому мазеру для МГД волн, в который накачиваются шумы и возмущения солнечного ветра, которые затем возбуждают магнитосферный волновод, далее фильтруются и усиливаются в магнитосферном альвеновском резонаторе в резонансной области, и высвечиваются к земной поверхности через полупрозрачные зеркала (ионосферы).

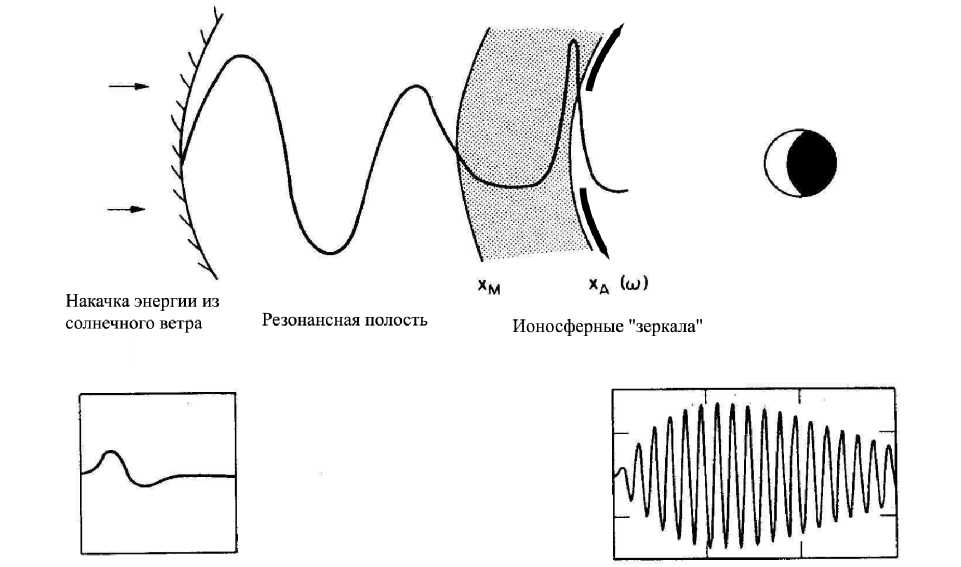
Рис. 16. Иллюстрация магнитосферы как природного мазера для МГД волн, в котором возмущения солнечного ветра возбуждают магнитосферный волновод. Далее они фильтруются и усиливаются в магнитосферном альвеновском резонаторе в резонансной области и высвечиваются к земной поверхности через полупрозрачные зеркала (ионосферы)

Поверхностная волна не является собственным решением МГД уравнений. Она проявляется при отклике на внешнее воздействие системы альвеновских резонаторов с широким спектром, сжатых в очень узкой области. Здесь происходит их интерференция, что приближенно сводится к образованию структуры типа поверхностной волны. Простейшая теория поверхностных волн строится для модели «плазменного ящика» с прямыми силовыми линиями, ограниченными сопряженными ионосферами. На границе двух полупространств (1 и 2) с разными альвеновским скоростями, разделённых переходным слоем толщины а, частоту ^w и декре- верхностной волны можно оценить по соотношениям [Archer et al., 2024]:

мент затухания y_sw  возбуждаемой по-

^ SW

222 z A 1 A 2 22 A1 + A 2

Yw = п ■      (   )

^sw   8 k+ k« y

A 1       A 2

При сильном перепаде альвеновских скоростей, V_A j >>  V_{A 2}, частота поверхностной моды определяется минимальной аль-веновской скоростью ^a sw ^ 2 2a A ! . При наблюдениях поверхностная волна проявляется как затухающий периодический отклик системы с частотой SW , пространственным радиальным масштабом ~ k - , и нерезистивным затуханием во времени с относительным декрементом ^y sw / ^a sw ~ ⁽ k y a ) из-за конверсии начального возмущения в альвеновский континуум.

Дневную магнитопаузу со ступенчатым скачком напряженности магнитного поля и плотности плазмы можно рассматривать как напряженную мембрану с отражающими границами в северной и южной ионосферах, которая может резонансно возбуждаться турбулентностью переход- ной области. МГД-моделирование реакции дневной магнитосферы на динамические импульсы давления солнечного ветра показало, что свойства возбуждаемых волн с дискретным спектром во внешней магнитосфере могут быть объяснены только поверхностной МГД волной на магнитопаузе.

Глобальные объемные и поверхностные МГД моды играют особую роль в волновой физике [ Леонович и Мазур, 2016]. Любая система более эффективно поглощает энергию набегающего турбулентного потока на собственной частоте глобальной моды. По сути, плазменная система с объемной или поверхностной волной работает как резонатор Фабри-Перро, обеспечивающий естественный процесс частотной фильтрации в турбулентной гелиогеофи-зической плазме.

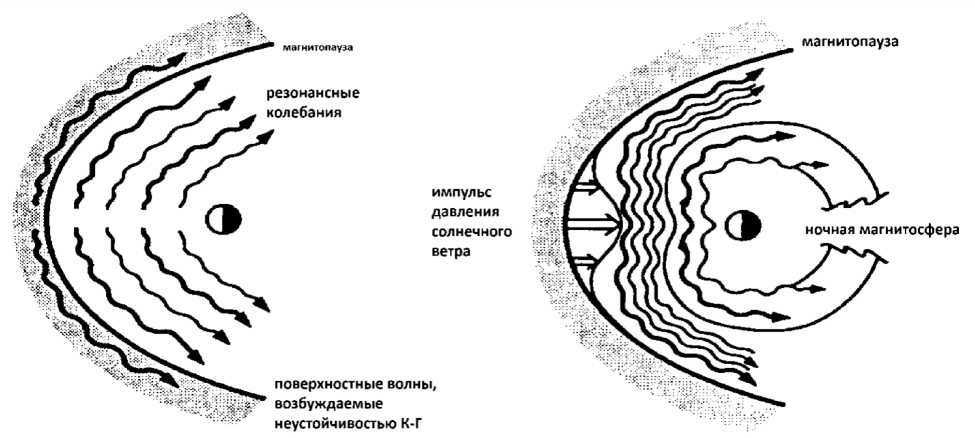
Рис. 17. Основные механизмы генерации МГД волн в околоземном космическом пространстве: флуктуации динамического давления солнечного ветра (слева) и неустойчивость Кельвина-Гельмгольца тангенциального разрыва между потоком плазмы солнечного ветра и магнитосферой

Источники пульсаций Рс4-5

Источником пульсаций Рс4-5 могут служить флуктуации динамического давления солнечного ветра (рис. 17). Кроме того, сама граница между магнитосферой и обтекающим ее потоком солнечного ветра может стать источником МГД волн при достаточно большом сдвиге скоростей благодаря неустойчивости Кельвина-Гельмгольца [Пудовкин и др., 1976]. Таким образом, неустойчивости тангенциального разрыва на утреннем и вечернем флангах являются одним из основных механизмов генерации МГД волн в околоземном пространстве. Порог возбуждения неустойчивости Кельвина-Гельмгольца зависит от параметров возмущения, но наиболее существенным фактором является скорость обтекания магнитосферы потоком солнечного ветра. Эти представления подтверждаются ростом интенсивности и длительности Рс5 пульсаций с ростом скорости солнечного ветра. Дальнейшая эволюция возбуждаемых колебаний внутри маг- нитосферы была описана в предыдущих разделах.

Источники пульсаций Рс3

Первичным источником УНЧ волн Рс3 диапазона является турбулентная область перед фронтом стоячей ударной волны, образующейся при набегании потока солнечной плазмы на земную магнитосферу (рис. 18). Возбуждение волн (upstream waves) происходит в форшоковой области в результате циклотронной неустойчивости пучков отраженных протонов на фронте ударной волны при ориентации силовых линий межпланетного магнитного поля (ММП) вдоль нормали к фронту ударной волны (квазипараллельная ударная волна) [ Гульельми, 1979]. Вблизи лобовой области ударной волн условие квазипараллельности означает малость конусного угла θ – угла между направлением ММП и линией Земля-Солнце. Эти соображения подтверждаются надежно установленным эффектом модуляции эффективности возбуждения Рс3 пульсаций ориентацией ММП (т. е. конусного угла ).

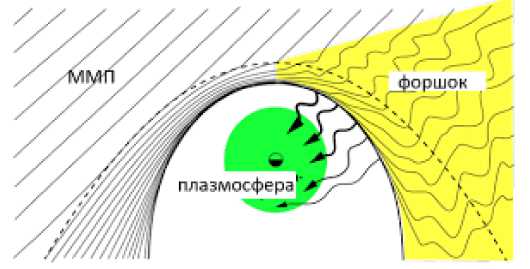
Рис. 18. Турбулентная область перед фронтом стоячей ударной волны (форшок) как источник волн Рс3 диапазона в магнитосфере

Частота возбуждаемой ЭМИЦ волны определяется комбинацией дисперсионного соотношения и резонансного условия, ^^ (VA I Ui №. Из-за слабого поля В в форшоке частота возбуждаемых волн попадает в диапазон Рс3. Далее, эти волны сносятся потоком солнечного ветра из форшока к фронту ударной волны и магнитослою. Затем ЭМИЦ излучения просачиваются через переходную область, проникают в магнитосферу, и в конечном счете попадают на Землю [Yumoto, 1986]. Эти соображения хорошо подтверждаются свя- зью между частотой волн в форшоке и величиной ММП планет, обладающих магнитосферой.

Методы наземного мониторинга околоземной плазмы с использованием волн Рс3-5

Для исследования плазменных процессов в ближнем космосе МГД волны имеют такое же значение, как сейсмические волны для изучения строения Земли. Однако есть принципиальное отличие в подходах к геофизическому использованию сейсмических и МГД волн. В отличие от сейсмо- логии, для геомагнитных пульсаций весьма ориентировочно известны свойства их источников (местонахождение, спектральный состав и т. п.). Тем не менее, существует принципиальная возможность использования регистрируемых на земной поверхности геомагнитных пульсаций Рс3-5 для МГД диагностики – определения свойств магнитосферной и ионосферной плазмы [Menk and Waters, 2013]. Физической основой МГД диагностики является эффект резонансной трансформации МГД волн в магнитосфере. Резонансная частота fA(ф) определяется для данной широты □ локальными свойствами распределения магнитосферной плазмы вдоль силовой линии, а добротность магнитосферного альвеновского резонатора – диссипативными свойствами ионосферы. Таким образом, уверенное выделение резонансных эффектов и наличие надежных методов экспериментального определения параметров магнитосферного альвеновского резонатора открывают возможность мониторинга плотности околоземной плазмы и проводимости ионосферы по наземным данным [Федоров и др., 1992].

Наиболее эффективным образом удается отстроиться от влияния спектра источника и выделить локальные резонансные особенности с помощью градиентного метода, основанного на прецизионных измерениях поля пульсаций на малой базе (~нескольких десятков км) [Pilipenko and Fedorov, 1993]. Для определения собственной частоты силовых линий, ее радиального градиента и ширины резонансной области наиболее надежным инструментом наземной МГД диагностики магнитосферы служит разновидность градиентно- го метода, основанная на расчете годографа отношения комплексных спектров сигнала на двух станциях. Этот метод позволяет получить непрерывное распределение резонансных частот и добротностей магнитосферного альвеновского резонатора в конечном интервале широт, даже выходящем за широтный интервал точек наблюдения. Используя экспериментально определенный профиль резонансных частот, можно проводить «гидромагнитную сейсмологию», т. е. восстанавливать радиальный профиль распределения магнитосферной плазмы.

Генерация низкочастотных волн энергичными частицами

Волновые возмущения в околоземном пространстве могут возбуждаться не только при непосредственном воздействии потока солнечного ветра на магнитосферу Земли, но и в результате генерации в неравновесной плазме. Неравновесные распределения энергичных частиц в магнитосфере, подобно инверсной заселенности атомной структуры, могут генерировать колебания в магнитосферном МГД мазере.

Волны могут обмениваться энергией с частицами благодаря поперечному электрическому полю волны ^E ⊥ , продольному электрическому полю ^E , и продольному магнитному полю ^B (строго говоря, из-за индукционного электрического поля, возбуждаемого вариациями компоненты ^B ). Для УНЧ волн, частота которых много меньше гирочастоты ионов ( ω << Ω ), изменение кинетической энергии частиц W описывается соотношением:

∂ B _‖

^∂ _∂ ^W _t = qV ‖ ⋅ E ‖ + q V D ⋅ E ⊥ + µ _{∂ t} ^‖

где № = mV 2 / 2 B — магнитный момент, q — заряд частицы.

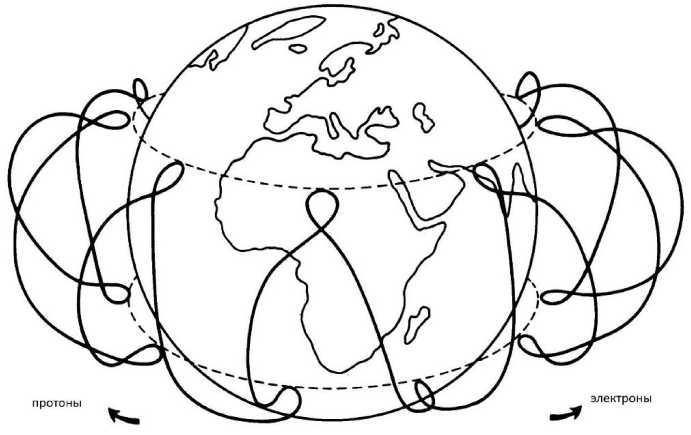
Рис. 19. Схематичная картина дрейфов частиц в неоднородном магнитосферном магнит- ном поле

Энергичные частицы, захваченные в магнитосферную ловушку, помимо быст- рого ларморовского вращения осциллируют с частотой b вдоль силовых линий (баунс-движение) между магнитными «пробками» – областей с сильным геомагнитным полем над ионосферами. Из-за радиальной неоднородности и кривизны магнитосферного магнитного поля частицы также испытывают магнитный дрейф в азимутальном направлении со скоростью u2                      „

V D = V d + V R , где V _d = ^ k b — градиентный

U 2

дрейф,   V R = 2OR

дрейф кривизны,

рек поля B 0 . В равновесной конфигурации радиальные градиенты магнитного поля К = d_r In В и давления плазмы к_р = д_г ln P не произвольны, а связаны с радиусом кривизны поля R соотношением ~г к _р + к в + — (1 + -) = 0. При этом

• 2    R 2

протоны дрейфуют на запад, а электроны – на восток. Схематично картина дрейфов частиц в магнитосферном магнитном поле показана на рисунке 19.

Наиболее эффективно обмен энергией между УНЧ волнами и частицами происходит в случае баунс-дрейфового резонанса:

un, и± - тепловые скорости вдоль и попе- ф - mad - Kq = 0                    (10)

где Qi = (Vd + Vr V R - усредненная угловая скорость магнитного дрейфа, K – номер баунс-гармоники. Волновой вектор ky связан с азимутальным волновым числом m в дипольном поле соотношением ky = m ILRE. Благодаря свойствам симметрии дрейфовый резонанс (K=0) может генерировать нечетные гармоники колебаний силовой линии (в том числе и основную гармонику), а баунс-дрейфовый резо- нанс K= 1 может генерировать четные гармоники колебаний силовой линии.

Будет ли в результате резонансного взаимодействия происходить перенос энергии от волны к частицам (бесстолкновительное затухание волны) или возбуждение волн (развитие неустойчивости), зависит от функции распределения частиц F ( W , x ) по энергии W и пространству. Выражение для скорости роста/затухания волны (инкремент/декремент) имеет вид:

∞

Y x Im ^

K =-∞

ω - ω   ∂ F

ω - m ω - K ω ∂ W

где <…> означает усреднение по про- странству ω=-[k⊥×∇⊥F]=

*   QdF / д W kyu κ

P

скоростей,

– частота лар-

моровского дрейфа плазмы, пропорциональная радиальному градиенту функции распределения. Для равновесного максвелловского распределения дF / d W < 0, и волна испытывает бесстолкновительное затухание <0. Возбуждение неустойчивости ( >0) может возникать, когда функ- ция распределения имеет инверсное распределение по энергиям (положительный наклон) dF / d W > 0 (распределение типа bump-on-tail). Инверсная функция распределения может естественным образом появиться в магнитосфере из-за дисперсии энергий, инжектированных в суббурю частиц, поскольку частицы с большей энергией дрейфуют быстрее, чем частицы с меньшей энергией.

Другой источник свободной энергии для роста плазменных неустойчивостей – резкие неоднородности давления энергичных протонов кольцевого тока. Дрейфовые кинетические неустойчивости из-за боль- ших градиентов давления плазмы могут развиваться при ^ < ®*. Физическая природа дрейфовых неустойчивости состоит в том, что при ® < ®* волна обладает отрицательной энергией, в результате чего бесстолкновительная диссипация при дF / д W < 0 приводит к возбуждению неустойчивости. Дрейфовые неустойчивости могут развиваться либо на внутренней, либо внешней кромке кольцевого тока. Скорости распространения колебаний в азимутальном направлении определяются скоростью ларморовского дрейфа плазмы, порядка первых км/c, и определяются знаком и величиной градиента давления горячей компоненты плазмы. Резонансное возбуждение частицами квазимонохромати-ческих колебаний диапазона Рс4-5 имеет место в фазу восстановления магнитной бури, когда неравновесные распределения горячих протонов медленно релаксируют к термодинамически устойчивому состоянию под действием кинетических неустойчивостей. Возбуждаемые колебания оказывают обратное влияние на распределение энергичных частиц, постепенно размывая резкие градиенты давления плазмы.

Хотя теория дрейфовых неустойчивостей, вызываемых неоднородностями горячей плазмы, активно развивается в физике плазмы, интерпретация наблюдений волн в магнитосферной плазме потребовала разработки новых теоретических моделей, учитывающих ее характерные особенности: конечное давление плазмы, сопоставимое с давлением магнитного поля ( ^в^ ¹ ); многокомпонентность плазмы -наличие холодных и горячих частиц; и анизотропию A = T / T ^-1 продольной и поперечной температур. Обнаруженные неустойчивости оказались новыми не только для космической геофизики, но и для физики плазмы в целом. Когда межмодовое зацепление поперечномелкомасштабных колебаний из-за неоднородности плазмы оказывается малым, зацепление различных мод в плазме конечного давления определяется эффектами конечного ларморовского радиуса ионов ρ . Возмущения с поперечными длинами волн, большими ларморовского радиуса, т. е. ( к_±р )² <<  1 , распадаются на независимые колебания – сжимаемую альвенов-скую волну и дрейфово-зеркальную моду магнитозвукового типа. В альвеновской моде в плазме конечного давления поддерживается баланс поперечного давления плазмы и магнитного поля p + B_nB ₀/4 п ~0 .

Магнитосферные частицы наиболее эффективно обмениваются энергией со стоячими волнами в резонансном случае (т. н. баунс-дрейфовый резонанс, см. выше), при этом структура УНЧ волн вдоль силовой линии накладывает ограничения на возможный тип резонанса. Обычно в теоретических моделях рассматривается либо альвеновские колебания, либо более сложные моды в плазме конечного давления, зацепленные с альвеновской волной. Прямые измерения этого масштаба практически невозможны, т. к. все спутниковые измерения во внешней магнитосфере проводятся вблизи экваториальной плоскости магнитосферы. Тем не менее, по-видимому, существуют колебания Рс5 диапазона с малым продольным масштабом, локализованные вблизи вершины силовой линии, которые не могут быть интерпретированы как альвеновские волны. Предположительно, таким колебаниями являются компрессионные Pc5 волны, т. е. волны сжатия магнитного поля. Традиционно эти волны объясняли как проявление дрейфово-зеркальной моды, которая для возбуждения требует большой анизотропии A и больших значений β. Другим возможным объяснением природы компрессионных Pc5 волн является дрейфовокомпрессионная мода, которая может возбуждаться в неоднородной плазме конечного давления при менее жестких условиях [Klimushkin, 2007]. Дрейфовокомпрессионные моды похожи на зеркально-дрейфовую моду, т. е. они представляют собой медленные магнитные волны сжатия и обладают диамагнитным свойством: противофазными колебаниями плазменного и магнитного давлений.

В начальную фазу магнитной бури интенсивная инжекция энергичных протонов и электронов может сопровождаться нерезонансной генерацией интенсивных ирре- гулярных возмущений типа Pi3 и стимулироваться интенсивными магнитосферными токами вдоль силовых линий. Полная картина возможных механизмов возбуждения УНЧ колебаний на разных фазах магнитных бурь активно разрабатывается, но еще не построена.

Наземный отклик на альвеновские колебания в сопряженных точках

Знание структуры стоячих колебаний силовых линий в магнитосферном альве-новском резонаторе важно для корректной гидромагнитной диагностики, понимания механизма возбуждения колебаний, определения эффективности резонансного взаимодействия волна-частица, и оценки эффектов взаимодействия волн с ионосферой [ Ляцкий и Мальцев, 1983]. Cтруктуру альвеновских колебаний можно определить по наблюдениям на геомагнитносопряжённых магнитных станциях. При высокой проводимости ионосферы (что заведомо выполняется в дневных условиях) на ионосферных концах колеблющейся силовой линии образуется узел электрического поля Е и смещения плазмы □ . Тогда, как качественно показано на рисунке 20 (слева), фундаментальная мода колебаний с пучностью в вершине силовой линии в магнитосферной экваториальной плоскости вызывают наземные пульсации магнитного поля с синфазными вариациями Н (С-Ю) компоненты. При низкой проводимости ионосферы фундаментальная моды дает противофазное соотношение (рис. 20, справа).

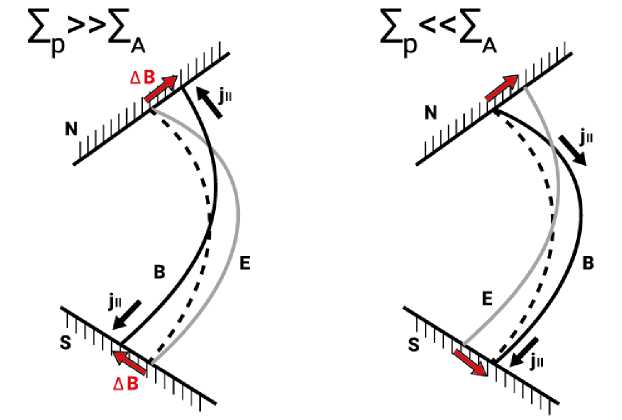
Рис. 20. Структура альвеновских колебаний вдоль силовой линии магнитного поля волны при высокой (слева) и низкой (справа) проводимости ионосферы

Наблюдения в сопряженных точках дают еще одну принципиально важную информацию. При рассмотрении источников нестационарных токовых систем в системе магнитосфера-ионосфера на качественном уровне различают генераторы тока, которые поддерживают фиксированный ток, и генераторы напряжения, в которых фиксировано напряжение. Эти ситуации можно представлять как электротехническую схему с генератором и внутренним сопротивлением. Если внутреннее сопротивление мало по сравнению с нагрузкой в цепи, то к нагрузке будет приложено фиксированное напряжение; тогда как если нагрузка мала по сравнению с внутренним сопротивлением, то на нее будет подаваться фиксированный ток. УНЧ возмущения также часто описывают с использованием этой электротехнической аналогии, при этом ионосфера работает как нагрузка, а процесс возбуждения колебаний в магнитосфере функционирует как генератор. В случае генератора магнитосферного тока наземный магнитный эффект должен быть почти одинаковым под освещенной или затемненной ионосферой, тогда как в слу-

B⁽ N )      S ⁽ N ) S ₄- i S S tan( k_AL )

- H   A    P     A

I S^ ” "Sf S - i S N tan( k L ) HA  P   A

Как вытекает из соотношения (12), асимметрия магнитных откликов зависит чае генератора напряжения отклик должен быть больше под высокопроводящей ионосферой.

Для разрешения дихотомии ток/напряжение магнитосферных возмущений эффективным подходом являются наблюдения на сопряженных станциях в условиях сильно асимметричных ионосфер. Важный аспект взаимодействия магнитосферных возмущений с ионосферой заключается в том, что нестационарные продольные токи могут взаимодействовать с ионосферой по-разному в режимах вынужденного возбуждения или резонансной раскачки. Проиллюстрируем это с помощью модели однородного «плазменного ящика» с асимметричными сопряженными ионосферами (рис. 13). Пусть на некоторой магнитной оболочке в экваториальной плоскости магнитосферы осциллирует поперечный ток j ( e ) . Из решения волнового уравнения для альвеновских колебаний (1) при условии отражения от ионосферы (16) следует отношение между наземным магнитным откликом в северном (N) и южном (S) полушариях:

от соотношения между временным масштабом возмущения и локальным альве- новским периодом TA. В случае нерезонансного низкочастотного возбуждения, когда т ^а (или kALO 1) отношение между наземными магнитными возмущениями в сопряженных точках:

B⁽N )

B S

у ( N )

ΣH у (S)

Σ _H

Таким образом, при нерезонансном ква-зистационарным возбуждении магнитный отклик должен быть больше под ионосферой с более высокой проводимостью, т. е. реализуется режим генератора напряже- ния. В случае возбуждения колебаний на резонансной частоте, т. е. когда ω→ ωA (или kAL ^ п /2), отношение магнитных откликов становится равным:

B⁽N ) B ^{( S} )

у ⁽ N ) у^{( S} )

Σ _H Σ _P

У( N ) у( S )

Σ _P Σ _H

Поскольку в реальной ионосфере ^ н / ^ p ~ const , из соотношения (14) следует, что отношение магнитных откликов в сопряженных точках не зависит от ионосферной проводимости, т. е. реализуется режим генератора тока.

Изменение режима магнитосферного генератора при переходе от нерезонансного к резонансному возбуждению аналогично антиотражательному покрытию в оптике, где входное сопротивление многослойной системы резко изменяется, когда длина волны падающего света кратна ширине слоя. Результаты сопряженных наблюдений различных типов УНЧ-возмущений хорошо согласуются с описываемой концепцией [Pilipenko et al., 2021]. Оказалось, что квазипостоянные нерезонансные возмущения, такие как глобальные магнитосферные системы продольных токов и SC на низких широтах, действительно соответствуют режиму генератора напряжения. Такие же магнитосферные явление, как Pc5 волны и конвективные вихри (Traveling Convection Vortices), следует рассматривать как резонансный от- клик магнитосферных силовых линий, соответствующий режиму генератора тока. Межполушарная симметрия/асимметрия в геомагнитных наземных откликах проявляется в различных магнитосферноионосферных явлениях, крупномасштабных токовых системах, авроральных сияниях, УНЧ волнах и импульсах, т. д.

Pc1 пульсации (ионно-циклотронные волны)

Пульсации диапазона Рс1 ассоциируются с электромагнитными ионноциклотронными (ЭМИЦ) волнами, дошедшими из магнитосферы до ионосферы и земной поверхности. ЭМИЦ волны наблюдаются в диапазоне частот от долей Гц до первых Гц, и являются характерной чертой внутренней магнитосферы [Kangas et al., 1998]. Они генерируются вблизи магнитосферной экваториальной плоскости в результате циклотронной неустойчивости при резонансном взаимодействии волн и ионов [Трахтенгерц, Райкрофт, 2011]. Дисперсионное соотношение и резонансное условие для ЭМИЦ волн имеет вид ш = kVJ1 -т/О- ---1 + т/°i--- ш-kV-° = 0      (15)

" A^V          i J1 + ( ш / °,.)( k „ / k )          ^{DD i}

Резонансное условие (15) означает, что частота волны с учетом допплеровского сдвига совпадает с циклотронной частотой ионов Ω . В неподвижной системе отсчета волны распространяются противоположно скорости движения частиц вдоль внешнего поля Во, поскольку т < Ц. Пороговое условие неустойчивости A/(A +1) > т/Цi. Анизотропия температуры A = T To -1, необходимая для развития неустойчивости, может возрасти вследствие бетатронного ускорения при инжекции протонов кольцевого тока во внутреннюю магнитосферу, или из-за скачков динамического давления солнечного ветра. ЭМИЦ волны могут генерироваться как ионами из плазменного слоя на открытых дрейфовых траекториях, так и ионами кольцевого тока на замкнутых дрейфовых траекториях. Инкремент нарастания ЭМИЦ волн становится заметным при условии u V. Таким образом, благоприятные условия для развития этой неустойчивости для горячей анизотропной плазмы с ионами с энергией 10–100 кэВ, возникают либо вблизи плаз-мопаузы, где высока концентрация фоновой холодной плазмы, либо за пределами геосинхронной орбиты L>7, где мало магнитосферное магнитное поле. Поперечный масштаб волны предположительно определяется режимом квазипараллельного распространения, когда эффективный поперечный волновой вектор k± < k* = k (т / Ц).

Обычно считается, что ЭМИЦ неустойчивость протонов кольцевого тока конвективная, т. е. область неустойчивости в вершине силовой линии работает как усилитель бегущих альвеновских волн [Demekhov, 2007]. Сами волновые пакеты при этом осциллируют между сопряженными ионосферами и испытывают усиление при каждом прохождении через экваториальную область магнитосферы (модель bouncing wave packet). Волновые пакеты, попеременно появляющиеся в сопряженных точках, характерны для дискретных Рс1 пульсаций («жемчужины»). Однако зачастую Pс1 пульсации наблюдаются в виде непрерывного излучения, что свидетельствует об абсолютном режиме неустойчивости, т.е. работе неустойчивости как генератора излучения. Модельные расчеты показывают, что конвективная неустойчивость может перейти в абсо- лютную при в A > 3/2 . Однако экспериментальных подтверждений условий развития разных режимов неустойчивости не найдено.

В многокомпонентной плазме с примесью тяжелых ионов (He+, O+) в той области, где частота пакета равна перекрестной частоте, может происходить инверсия поляризации, и частичное отражение и поглощение волны. Это может приводить к образованию интервалов поглощения в спектральной структуре ЭМИЦ волн. Пример такой структуры со спектральным пробелом вблизи частоты ионов гелия приведен на рисунке 8.

Таким образом, интенсивность и частота появления волн Pc1 на земле определяются процессами генерации в приэкваториальной плоскости, распространения через магнитосферную плазму вдоль силовых линий до верхней ионосферы, и прохождения через ионосферу к Земле. В диапазоне Pc 1 ионосфера начинает проявлять резонансные и волноводные свойства, которые рассматриваются в последующих разделах.

Импульсные ночные колебания Pi2-Pi3

Интерес к Pi2 пульсациям связан с тем, что они возникают при резкой активизации магнитосферной активности – начале взрывной фазы суббури (breakup) и по существу являются «маркером», отмечающим переход медленной фазы роста возмущения ночной магнитосферы во взрывную фазу [ Olson, 1999]. Pi2 также могут быть откликом на импульсные потоки плазмы в хвосте магнитосферы (bursty bulk flows). Возбуждение Pi2 пульсаций сопровождается интенсификацией полярных сияний, ионосферными и продольными токами, высыпанием энергичных электронов и другими процессами, происходящими во время взрывной фазы суббури [ Keiling and Takahashi , 2011].

Вопрос о механизмах генерации Рi2 еще не решен окончательно. По-видимому, Pi2 пульсации на авроральных широтах и на низких широтах имеют различную природу. Pi2 пульсации в высоких широтах предположительно генерируются за счет осцилляций токовой системы суббуревого токового клина (substorm current wedge). При этом возмущение из хвоста магнитосферы переносится в высокоширотную ионосферу продольными токами. Период этих затухающих колебаний много меньше, чем период фундаментальной альвеновской моды на авроральных широтах, поэтому их нельзя представлять просто как транзиентные альвеновские колебания силовых линий. Несмотря на большое число предложенных гипотез, четкого понимания механизма формирования спектрального состава высокоширотных Pi2 пока нет.

Pi2 пульсации на низких широтах интерпретируются как проявление глобальных БМЗ колебаний ночной плазмосферы (рис. 21). Эти БМЗ колебания практически без ослабления проникают через ночную ионосферу к земной поверхности и обуславливают синхронный глобальный отклик на низких широтах. Пример таких колебаний, практически синхронных как в верхней ионосфере, так и на сети низкоширотных наземных станций, приведен на рисунке 10.

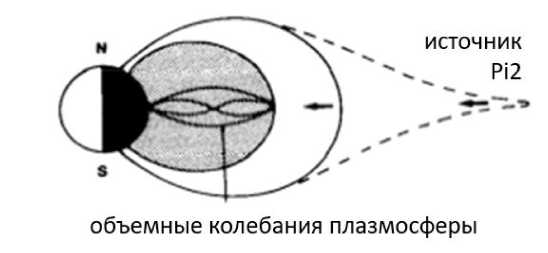
Рис. 21. Pi2 пульсации на низких широтах как глобальные БМЗ колебаний ночной плазмосферы

Высказывалось немало гипотез о происхождении Pi3/Ps6 пульсаций – квазипе-риодической последовательности импульсов с квази-периодом ~10–20 минут на фоне суббуревой магнитной бухты. Их объясняли вариациями параметров межпланетной среды, возникновением периодического режима магнитосферноионосферного взаимодействия, квазипери-одическим режимом пересоединения в токовом слое хвоста магнитосферы, неустойчивостями горячей компоненты магнитосферной плазмы [ Keiling , 2009]. Высказывались предположения, что пульсации Pi 3 могут быть связаны с собственными колебаниями магнитного хвоста Земли.

В отличие от других типов УНЧ возмущений (пульсации Pc3-5) пульсации Pi3 вряд ли связаны с резонансом силовых линий в магнитосфере, поскольку их период больше, чем период альвеновской моды на авроральных широтах. Хотя высказывались предположения, что столь большой период может быть связан с вытягиванием силовых линий геомагнитного поля в хвост магнитосферы во время сильных суббуревых возмущений. Возможным источником возбуждения пульсаций Рi3 может быть развитие баллонной неустойчивости. Действительно, баллонная мода, представляющая собой связанную альве-новскую и ММЗ моды, имеет две ветви. Период «альвеновской» ветви примерно совпадает с альвеновским периодом колебаний силовой линии TA, а поляризация этой ветви смешанная (Bz~B□ □□□ «Медленная» ветвь баллонных колебаний имеет гораздо больший период T>>TA, а ее поляризация соответствует компрессионной моде (Bz>>B □ □ .

Не исключено, что появление Pi3 пульсаций обусловлено несколькими разными механизмами. Таким образом, хотя существование Pi3 пульсаций общеизвестно, их физический механизм остается невыясненным до конца. Фундаментальный вопрос – почему для некоторых суббурь на магнитную бухту наложены Pi3 пульса- ции, а для некоторых нет – также не решен.

Взаимодействие магнитосферных УНЧ волн с ионосферой

Передача энергии из околоземной среды в земную атмосферу происходит в ионосфере, поэтому описание процессов взаимодействия УНЧ волн с ионосферой имеет ключевое значение для солнечноземной физики. К тому же наземные наблюдения зачастую являются единственным источником информации об УНЧ волновой активности в магнитосфере. Однако даже для горизонтально однородной ионосферы процесс взаимодействия падающей МГД волны с системой ионосфера-атмосфера-Земля довольно сложен – он включает в себя взаимную трансформацию альвеновской и БМЗ волн в анизотропной ионосфере, суперпозицию падающих и отражённых волн, связь с электрической и магнитной модами в атмосфере [ Alperovich and Fedorov , 2007].

Качественные представления о прохождении МГД волны к земной поверхности можно получить на основе модели «тонкой» ионосферы, в которой ионосфера представляется тонкой пленкой с интегральными холловской и педерсеновской проводимостями, находящейся на высоте h над земной поверхностью [Ляцкий и Мальцев, 1983]. Эта модель хорошо описывает взаимодействие крупномасштабных МГД мод с системой ионосфера-атмосфера-земля, для которых скин-длина и длина волны в ионосфере много больше толщины проводящего слоя Е (диапазон Рс3-5 и Pi2-3). Для магнитосферных колебаний ионосфера является частично отражающей и поглощающей стенкой, на которой выполняется граничное условие импедансного типа By =µ0ΣPEx при z= L.

При распространении альвеновских волн через ионосферу происходит поворот на □ □□ эллипса поляризации, т. е. наиболее выраженная в резонансных колебаниях в магнитосфере азимутальная компонента поля на земной поверхности будет наблюдаться как меридиональная (североюжная) компонента, ^B y ^{→ H} , а радиальная компонента будет соответствовать компоненте восток-запад (D), B x ^→ D Этот поворот вызван тем, что наземные магнитные возмущения, создаваемые продольным током, переносимым альвенов-ской волной, и вызываемыми им педерсе-новскими токами растекания по ионосфере, почти полностью компенсируются. В результате наземный магнитный отклик создается холловскими токами.

Характерные особенности отражения альвеновских волн от тонкой ионосферы видны из выражения для коэффициента отражения:

Σ p -Σ A sin I R =

Σ +Σ sin I pA

где I – наклонение геомагнитного поля (для вертикального поля I = π /2). Альве-новские волны хорошо отражаются от ионосферы при сильном контрасте между ионосферной проводимостью □ р и волновой проводимостью □ а. Это условие хорошо выполняется для дневной магнито- сферы, где □ Р>> □ A. Джоулева диссипация в ионосфере является одним из основных механизмов диссипации колебаний силовых линий, и определяет декремент затухания γ и ширину области альвеновского резонанса в магнитосфере δm:

γ = δ^m = ¹ ln | R | ωaπn

где a – поперечный размер неоднородности альвеновской скорости в магнитосфере, n – номер гармоники колебаний.

При прохождении через ионосферу происходит расплывание резонансной области в соответствии с соотношением

• 3    ^ d m + h . Наземный отклик в X-

• компоненте на тороидальные альвенов-ские колебания с амплитудой B(m) над ионосферой дается формулой:

, . У

B = B (m) ±я xy

L P exp (- kh)

Здесь k – горизонтальный волновой вектор возмущения. Соотношение (18) показывает, что мелкомасштабные возмущения с масштабом меньше, чем высота ионосферы (kh>>1), экранируются от наземных магнитометров. Для альвеновских волн с очень малыми поперечными масштабами (<2 км) следует дополнительно учитывать

( m )

-x— = 1 - ip Bx где Vc = (PoLc ) 1 - «каулинговская» скорость в ионосфере, определяемая кау-линговской проводимостью Lc = Sp + L2H / Lp. Параметр р контролирует прохождение БМЗ моды через ионосферу к земной поверхности: при p<<1 ионосфера прозрачна для БМЗ волн (что заведомо выполняется для ночной ионосферы), а ионосферное поглощение проявляется при p~1 в дневные часы. Поворота эллипса поляризации при прохождении БМЗ через ионосферу не происходит.

Для более высокочастотных пульсаций диапазона Рс1 приближение тонкой ионосферы становится неприменимым. Характерной особенностью ионосферы в этом частотном диапазоне является наличие волновода и резонатора, которые могут накапливать энергию электромагнитных волн в диапазоне от долей Гц до нескольких десятков Гц: ионосферный альвенов-ский резонатор (ИАР) и ионосферный волновод для БМЗ волн [Demekhov, 2012]. ИАР образуется за счет отражения альве-новских волн от резкого градиента вертикального профиля альвеновской скорости VA(z) на высотах около 103 км, где длина сильное поглощение из-за столкновитель-ной диссипации в ионосфере.

Взаимодействие БМЗ волны с системой ионосфера-атмосфера-Земля принципиально отличатся от взаимодействия альве-новской волны. Соотношение между возмущением горизонтальной магнитной компоненты над ионосферой и наземным откликом имеет вид:

ah

P = —

V

волны становится сопоставимой с размером неоднородности, т. е. происходит нарушение приближения геометрической оптики. Нижней границе ИАР служит проводящий Е-слой ионосферы. Наземные проявления ИАР – множественные спектральные полосы, разделенные по частоте на f ~0,3–0,5 Гц, регулярно наблюдаются в ночное время на низких, средних, и даже авроральных широтах. Резонансные свойства ионосферы обеспечивают зависимость свойств пропускания/отражения Pc1 пульсаций от частоты. Таким образом, ионосфера с учетом наличия ИАР может действовать как многодиапазонный полосовой фильтр для магнитосферных ЭМИЦ волн, формируя спектральную структуру излучений Pc1 , наблюдаемых на Земле.

Волновод для БМЗ волн образуется в области минимума альвеновской скорости в F-слое ионосферы. В результате магнитосферная ЭМИЦ волна внутри ионосферы частично преобразуется в волноводную моду, которая переносится на тысячи километров относительно места падения волны на ионосферу. Волноводные моды с частотой ниже критической частоты вол- новода (~0.5 Гц) не могут распространяться вдоль ионосферы. Горизонтальное распространение в волноводе наиболее эффективно вдоль магнитного меридиана. Таким образом, ионосфера функционирует как огромная «приемная антенна», собирающая магнитосферные ЭМИЦ сигналы с большой области вокруг наземного наблюдателя. Наземные наблюдения с использованием сети магнитометров показали, что амплитуда волны Pc1, распространяющиеся из области инжекции, спадала определенным образом: затухание было очень быстрым (~10 дБ/100км) в центре инжекции, но становилось намного слабее (~2.5 дБ/100км) в области за пределами ~500 км от центра.

Мелкомасштабные УНЧ волны

Спутниковые наблюдения с высоким пространственно-временным разрешением во время различных геофизических процессов показывают, что большая плотность мощности электромагнитных возмущений имеет тенденцию концентрироваться в малых временных и пространственных масштабах [Pilipenko and Enge-bretson, 2002]. Таким образом, импульсные и мелкомасштабные процессы, несмотря на их относительно непродолжительность и малый масштаб, могут давать суще- ственный вклад в энергетический обмен между геофизическими средами. В качестве примера импульсного энергообмена в системе магнитосфера-ионосфера-атмосфера можно вспомнить взрывной процесс с наибольшим энерговыделением в околоземной космической плазме – магнитосферную суббурю. Механизм возникновения суббури пока не установлен, но, вероятно, он связан с мелкомасштабными процессами вне области применимости идеальной МГД.

Процессы во внешней ночной магнитосфере ответственны за многообразные электромагнитные структуры, регистрируемые над авроральной областью. Интенсивные электрические поля и токи с поперечными масштабами менее нескольких десятков км часто регистрируются спутниками в окрестности ярких дискретных авроральных дуг. Были получены экспериментальные свидетельства в пользу волнового альвеновского механизма переноса электромагнитной энергии из плазменного слоя и хвоста магнитосферы в авроральную ионосферу. Дополнительная энергия для интенсификации аврорального свечения, т. н. «альвеновская аврора», может поступать через волновой канал, как схематично показано на рисунке 22.

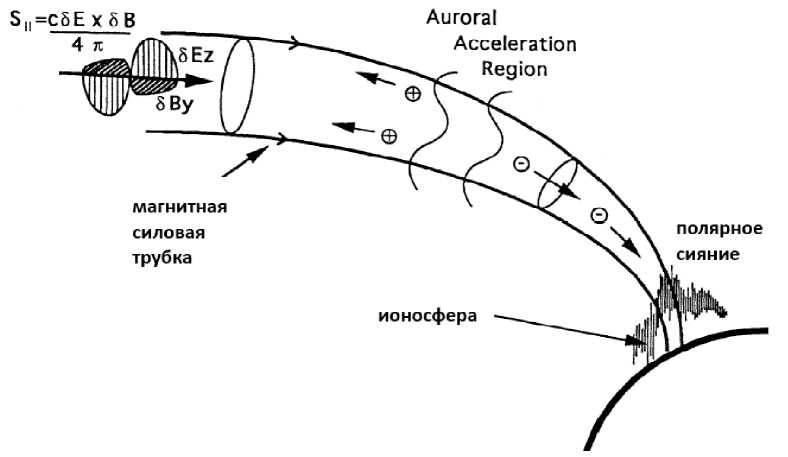
Рис. 22. Механизм формирования альвеновской авроры в силовой трубке с AAR (auroral acceleration region).

Мелкомасштабные электромагнитные возмущения УНЧ диапазона имеют ряд характерных особенностей по сравнению с возмущениями в идеальной МГД. В двухжидкостной МГД при учете кинетических и дисперсионных эффектов дисперсионное соотношение для альвенов-ских волн модифицируется, и вместо ω ^≡ ω A ^{= kV} A , имеем:

• -    в       кинетическом       пределе

a = a a J1 + kI pi ;

ω

A

• -    в инерционном пределе

  J +k /^

  
  

где Аг = c / ape - инерционная электронная длина, ω – электронная плазменная ча- стота.

Когда поправки не очень велики, эти дисперсионные соотношения могут быть объединены в одно aQ a_A ^ 1 ± k 2 р 2 , где

P d □ P i +А 2 - обобщенный дисперсионный радиус.

В отличие от альвеновских волн в приближении идеальной МГД, мелкомасштабные структуры с масштабами, сравнимыми с радиусом дисперсии ρ^d , обладают собственным продольным электрическим полем ^E следующего вида I E 1 = ^{( k} i ^p d )² ( ^k / ^k i ) I E 1 1 . Благодаря

АФ = Q j

Продольную проводимость силовой трубки K=1/Q можно оценить как K □ Ne2 / mue. Благодаря возникающему продольному электрическому полю авроральные электроны могут переносить существенные токи между магнитосферой и нижней ионосферой даже при очень малых значениях конуса потерь. Хотя ряд концептуальных проблем продольных электрических полей остается не до конца выясненным, нелокальный закон Ома (20) широко используется в физике авроральной плазмы. По существу, возникновение продольной разности потенциала является кинетическим эффектом, однако в рамках этому полю дисперсионные альвеновские волны могут эффективно ускорять авроральные электроны.

В бесстолкновительной тепловой плаз- ме на авроральных широтах широко распространенное представление об эквипотенциальности силовых линий может нарушаться, что приводит к появлению аномального продольного электрического поля E∗ , ускорению и высыпанию элек- тронов. Значительное нерезиститвное падение потенциала вдоль силовых линий может создаваться пробочным механизмом (mirror forces). Пробочный механизм обуславливает появление продольного электрического поля E за счет разницы питч-угловых распределений электронов и ионов квази-нейтральной плазмы. В кинетической теории удается рассчитать само- согласованное стационарное распределение потенциала (s) и продольного тока jo(s) вдоль силовой линии. В общем слу- чае, j является функционалом от (s), т. е. j =j( (s)). Однако в широком диапазоне параметров плазмы оказывается справедливым линейное нелокальное соотношение между вытекающим из ионосферы током j и падением потенциала (формула Knight) [Vogt, 2002]

или j = K ΔΦ (20)

МГД приближения можно полагать, что существует нелокальная вольтамперная характеристика, следующая из кинетического рассмотрения и связывающая вытекающий ток j с падением потенциала ΔΦ .

Ключевым фактором, влияющим на ускорение авроральных электронов, является продольная компонента электрического поля УНЧ волны. Среди возможных механизмов передачи энергии авроральным электронам, важную роль играет взаимодействие магнитосферных альвенов-ских волн с областью продольного падения потенциала над авроральным овалом.

Наличие области ускорения авроральных частиц (auroral acceleration region – AAR) – локализованной по высоте области со значительным падением электрического потенциала вдоль силовых линий, является важной особенностью системы магнитосфера-ионосфера на авроральных широтах. Наличие AAR видоизменяет свойства альвеновской волны, в частности приводит к появлению у нее продольного электрического поля E_n □ j_a ( Q / d ) , где d - толщина AAR области. Предположительно, этот механизм ответственен за образование «альвеновской авроры» – ускорение электронов и уярчение полярных сияний под действием магнитосферных УНЧ волн.

Наиболее эффективно конверсия энергии альвеновских волн в ускорение авроральных электронов происходит при поперечных масштабах волны k_± Л_А ~ 1 , где параметр λ = Q Σ. При типичных параметрах авроральной области масштаб λ A составляет первые десятки км. Если квази-стационарные продольные поля приводят к формированию моноэнергетических пучков высыпающихся электронов (т. н. inverted V структуры), то в «альвеновской авроре» ускорение и высыпание захватывает большой диапазон энергий, как схематично показано на рис. 23.

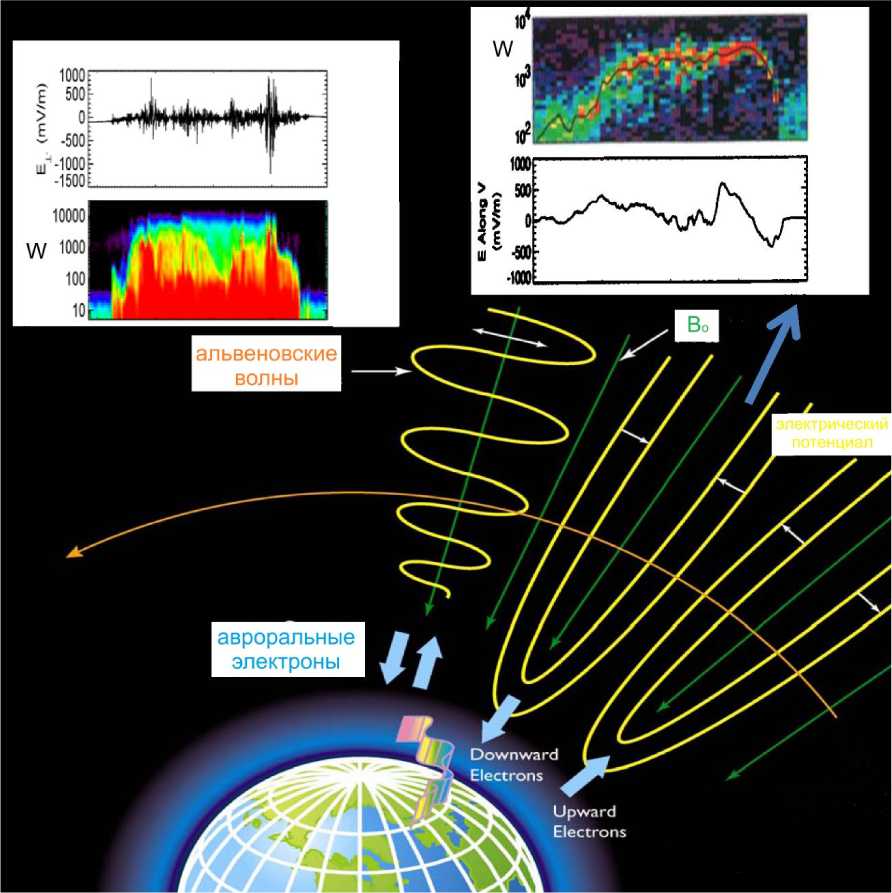
Рис. 23. Энергетические спектры авроральных электронов в области альвеновской авроры (слева) и в области квазистационарных продольных полей (inverted-V структуры)

УНЧ волны как активный фактор космической погоды

К настоящему времени космическая геофизика достигла уровня, позволяющего ставить вопрос о реальном прогнозе «космической погоды». Эта проблема становится все более актуальной, поскольку современные высокотехнологичные системы, особенно спутниковые, весьма чувствительны к воздействию электромагнитных полей и радиации. Несмотря на мощный арсенал современной космической геофизики – солнечные радиотелескопы, космические станции между Землей и Солнцем, флотилии спутников на околоземных орбитах, сети наземных радаров и магнитометров, и т. п. – проблема мониторинга и прогноза космической погоды не стала «чисто инженерной». Солнечноземное взаимодействие оказалось отчасти схожим с сейсмотектоническими процессами. Постоянно поступающая энергия потока солнечной плазмы не просто диссипирует в околоземном пространстве, а накапливается с ночной стороны магнитосферы, затем спонтанно высвобождается в виде мощных потоков ускоренных частиц и интенсивных глобальных токов. Магнитосферные бури и суббури оказываются своего рода «космотрясениями», механизмы которых остаются до сих пор окончательно невыясненными.

Геомагнитные УНЧ волны в широком интервале пространственных и временных масштабов традиционно используются в качестве одного из основных средств «мониторинга космической погоды» и «диагностики околоземного пространства» [Troitskaya and Guglielmi, 1967]. Однако, все больше появляется экс- периментальных свидетельств того, что УНЧ возмущения, заполняющие околоземное пространство, не только индикатор, но и активный фактор воздействия на околоземную среду и на наземные и спутниковые технологические системы. Резкие изменения геомагнитного поля могут приводить к сбоям в работе энергетических и транспортных систем, вызванных геоин-дуцированными токами (ГИТ), которые индуцируются в протяженных заземленных системах. При этом, хотя космическая погода активирует глобальные электромагнитные и плазменные процессы в околоземной среде, однако наибольший риск ГИТ связан не непосредственно с крупномасштабными процессами с огромным выделением энергии, а с более локальными и быстрыми процессами [Пилипенко, 2021]. Оказалось, что электрические сети наиболее чувствительны к помехам от естественных геоэлектрических полей, которые вызываются геомагнитными пульсациями Pi3/Ps6 с периодами порядка первых мин – десятков мин. Именно они вызывают наиболее интенсивные всплески ГИТ с размахом до сотен А в ЛЭП и способствуют возникновению ГИТ в протяженных инженерных системах, таких как железные дороги и трубопроводы [Belakhovsky et al., 2019]. В качестве примера, на рис. 24 приведено сопоставление ГИТ в ЛЭП на Кольском полуострове с магнитными вариациями на близкой магнитной станции во время магнитной бури 27-28 мая 2017 г. Видно, что возбуждение всплесков ГИТ вызвано воздействием Pi3 пульсаций, наложенных на магнитную бухту, во время развития магнитной бури.

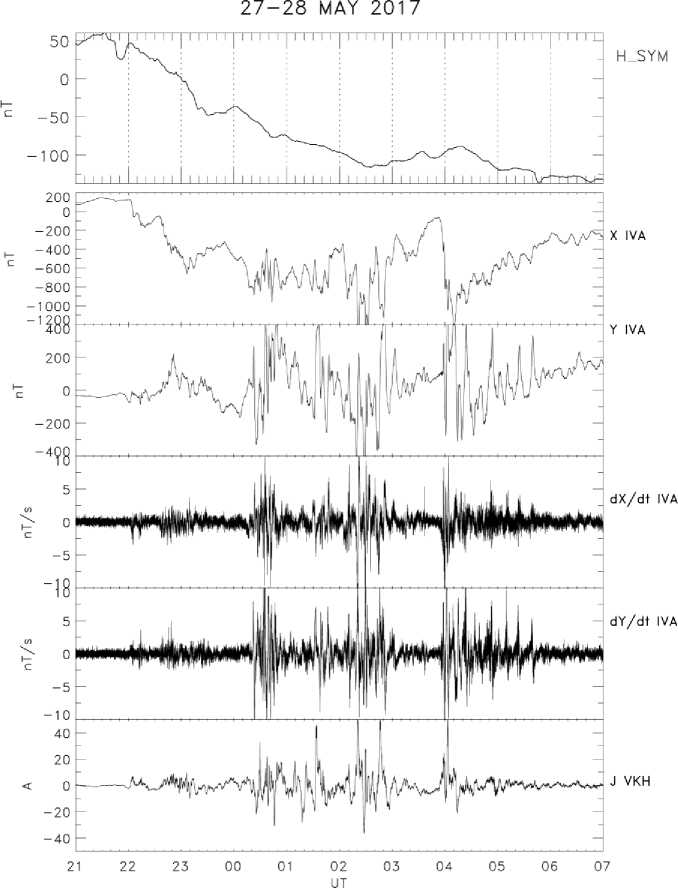
Рис. 24. Возбуждение ГИТ в ЛЭП «Северный Транзит» геомагнитными пульсациями Pi3 . Сверху вниз показаны вариации индекса SYM-H, характеризующего интенсивность магнитной бури, магнитограммы горизонтальных магнитных компонент на близкой станции IVA, вариабельность магнитного поля dX/dt и dY/dt на той же станции, и вариации ГИТ на подстанции «Выходной».

Разработанные в мире глобальные МГД модели магнитосферы хорошо воспроизводят ее глобальную динамику, но не в состоянии смоделировать возбуждение среднемасштабных Pi3 пульсаций. В результате эти модели оказались неспособными предсказывать величину вариабельности геомагнитного поля и соответственно ГИТ при возмущениях космической погоды. По аналогии с гидродинамикой можно предположить, что взаимодействие турбулентного потока солнечной плазмы с магнитосферой Земли будет принципиально отличаться от взаимодействия с ламинарным потоком. Поэтому уровень турбулентности в околоземном пространстве, который отражается в интенсивности УНЧ волн, может быть одним из ключевых параметров, характеризующих космическую погоду.

Динамика УНЧ волн в земной магнитосфере тесно связана с динамикой частиц. Магнитосферные УНЧ волны могут эффективно модулировать потоки частиц, и приводить к модулированному высыпанию в ионосферу, создающему помехи в транс-ионосферной радиосвязи. УНЧ волны могут модулировать полное электронное содержание (ПЭС) ионосферы, созда- вая возмущения для сигналов спутниковых навигационных систем GPS/GLONASS, модулировать ускорение и высыпание авроральных электронов, и даже вызывать локальный нагрев термосферы. Таким образом, ионосфера оказывается не только пассивным экраном для магнитосферных волн, но и сама может искажаться под их воздействием.

УНЧ волны и динамика радиационного пояса

Электродинамика околоземного пространства определяется солнечным ветром и ММП, но ускорение магнитосферных электронов до релятивистских энергий и усиление внешнего радиационного пояса Земли обусловлено внутримагнитосфер-ными процессами. В бесстолкновительной космической плазме поток солнечного ветра не взаимодействует напрямую с захваченными электронами магнитосферы, и электромагнитные поля играют роль посредника, передающего энергию от частиц низкой энергии небольшой группе частиц высокой энергии. Динамика внешнего радиационного пояса определяется сложным действием нескольких механизмов ускорения, переноса и потерь энергичных частиц. Главная фаза сильной магнитной бури сопровождается быстрым падением потока МэВ-электронов, за которым следует медленное адиабатичсекое восстановление до предбуревого уровня. Однако почти в 50% бурь электронные потоки нарастают на 2-3 порядка, далеко за пределы адиабатического уровня. Усиление потоков релятивистских электронов происходит сначала быстро в сердцевине пояса за несколько часов (L~3-4), а затем медленно (за дни-недели) на больших магнитных оболочках (L>6). Механизм ускорения магнитосферных электронов до релятивистских энергий до сих пор остается нерешенной проблемой космофизики.

Понимание динамики внешнего радиационного пояса представляет интерес не только для академических исследователей, т. к. резкие «ухудшения» космической погоды оказывают негативное влияние на работу космических аппаратов. Наиболее опасным является воздействие энергичных частиц, способных, в зависимости от энер- гии, вызвать сбои в электронике, дифференциальную зарядку внешних и внутренних диэлектриков с последующим пробоем, повреждение панелей солнечных батарей и др. Серьезные аномалии в работе магнитосферных космических аппаратов наблюдались сразу после резкого подъема потока релятивистских магнитосферных электронов, в связи с чем эти электроны даже получили название «электроны-убийцы» (killer electrons). Интересно, что увеличение интенсивности потоков «электронов-убийц» тесно следует за увеличением волновой активности в магнитосфере, характеризуемой «волновым индексом», пропорциональным интегральной спектральной плотности магнитных вариаций в Рс5 диапазоне на наземных станциях [Pilipenko et al., 2017]. Интенсивный рост потоков релятивистских электронов хорошо соответствовал изменениям глобального УНЧ индекса, так что этот индекс гораздо лучше характеризует динамику электронов, чем любой другой геомагнитный индекс. Эта закономерность позволила высказать гипотезу, что именно Рс5 волны ускоряют энергичные электроны до релятивистских энергий на восстановительной фазе магнитных бурь [Mann et al., 2013].

ям

Vd[km/s] □ 8.5L2W[MeV]g(a) Td[min] □ где – питч-угол частицы на экваторе. Из этого соотношения следует, что ~1 мэВ электроны, дрейфующие на оболочке L~6,

----------g(a)   g(a) = 0.7 + 0.3 sin a

LW [MeV]                            ⁽²¹⁾

могут резонансно взаимодействовать с волнами в диапазоне Рс5 (5-10 мин).

Рис. 25. Качественная иллюстрация работы магнитосферного «геосерфотрона», приводящая к резонансному ускорению дрейфующих вокруг Земли энергичных электронов электрическим полем Рс5 пульсаций

Высокая корреляция между мощностью УНЧ вариаций и динамикой электронов в значительной степени также может быть обусловлена пульсациями Pi3 . Время прохождения дрейфующего электрона через мелкомасштабную структуру Pi3 значительно меньше периодичности Pi3 , поэтому их можно считать квазистационарной структурой с интенсивным азимутальным электрическим полем. Наиболее эффективным образом будет резонансно ускоряться группа частиц с такими энергиями, что период прохождения через возмущенную область кратен периоду возмущения, a = m ^ . Ускорение частиц по описанному механизму можно назвать «геосинхротроном». Какой из механизмов ускорения электронов радиационного пояса – радиальная диффузия под действием УНЧ пульсаций или локальное ускорение при взаимодействии с ОНЧ излучением кГц диапазона (хоры), является преобладающим – остается нерешенной проблемой.

УНЧ волны могут приводить не только к ускорению электронов радиационного пояса, но и вызывать их сброс в атмосферу. ЭМИЦ волны диапазона Рс1 могут резонансно рассеивать по питч-углам электроны релятивистских энергий и быть ответственными за опустошение радиационных пояса Земли. ЭМИЦ излучения также ограничивают время жизни энергичных протонов кольцевого тока и вызывают локализованное протонное сияние за счет резонансного воздействия на ~100 кэВ протоны. Однако волновой пакет типичных пульсаций Рс1 имеет малые масштабы в поперечном направлении, поэтому насколько заметным может оказаться его воздействие на радиационный пояс или кольцевой ток в целом – остается невыясненным.

Возмущения геомагнитного поля антропогенного происхождения

Детальное знание морфологии и природы естественных вариаций геомагнитного поля позволяют среди кажущегося хаоса возмущений, просачивающихся на Землю из околоземного пространства через ионосферу, выделить слабые аномальные сигналы (шумы, импульсы, транзиенты), не связанные с источниками космической природы:

• -    Антропогенные возмущения, вызванные взрывами и стартами ракет.

• -    Отклики на метеоявления (ураганы, тайфуны, грозы);

• -    Сейсмо-электромагнитные шумы и импульсы, связанные с процессами в зонах разрушения горной породы во время подготовки землетрясений [ Surkov and Hayakawa, 2014].

Все эти процессы связаны с выделением большого количества энергии и затрагивают все геофизические оболочки (литосферу, атмосферу, ионосферу и магнитосферу) и геофизические поля [ Pokhotelov et al., 1995]. В годы холодной войны именно появление специфических геомагнитных пульсаций диапазона Рс1 оказалось наиболее надежным индикатором для дистанционного обнаружения высотных ядерных взрывов в атмосфере и ионосфере.

В конкретной ситуации могут реализоваться различные механизмы воздействия взрывов и землетрясений на ионосферу и геомагнитное поле. Распространяющиеся от места взрыва или землетрясения сейсмические волны благодаря индукционному эффекту порождают сопутствующий электромагнитный сигнал [ Surkov and Pilipenko, 1997]. Акустическая волна от взрыва или землетрясения, достигающая ионосферных высот, индуцирует токи в проводящем слое ионосферы ( Е -слой). Система ионосферных токов оказывается незамкнутой и порождает продольные токи вдоль силовых линий геомагнитного поля на фронте акустического импульса. Импульс продольного тока может быть зарегистрирован на низкоорбитальном спутнике как всплеск возмущения поперечной компоненты геомагнитного поля. Кроме того, индуцируемые акустической волной взрыва или землетрясения в ионосфере токи возбуждают распространяющиеся вдоль ионосферы МГД волны.

Электромагнитные УНЧ эффекты сопровождают и запуски мощных ракет. Продукты сгорания от факела ракетного двигателя подобно снежному плугу расталкивают плазму в нижних слоях ионосферы и генерируют интенсивные токи и гидромагнитные шумы. Часть этих шумов, с частотами более 1 Гц, захватывается в ионосферный БМЗ волновод и распространяется на значительные расстояния от места старта. Такие возмущения диапазона Рс1 наблюдались на сети индукционных магнитометров после запусков межконтинентальных ракет.

Заключение

УНЧ электромагнитные поля являются эффективным средством для слежения за процессами в различных геофизических средах: магнитосфере, ионосфере, атмосфере и литосфере. Излучения УНЧ диапазона сопровождают все энергетически мощные геофизические процессы и служат одним из методов их диагностики и мониторинга. Исследования нетривиального эффекта резонансной трансформации МГД колебаний привели к созданию надежно обоснованных наземных методов гидро-магнитной диагностики магнитосферы по данным УНЧ волн. УНЧ излучения могут эффективно возбуждаться и при сейсмогенном или антропогенном воздействии на геофизические среды. Геомагнитные УНЧ волны оказываются не только одним из основных средств диагностики околоземного пространства, но и активным фактором воздействия как на околоземную среду, так и на наземные и спутниковые технологические системы. Однако потенциальные возможности УНЧ волн для мониторинга процессов в околоземном пространстве далеко не исчерпаны и, по существу, «гидромагнитная сейсмология» только зарождается. Качественно новый уровень в геофизических исследованиях произойдет при переходе от использования узко специализированных станций (магнитных, сейсмических, ионосферных, метеорологических) к развертыванию единой сети автономных комплексных геофизических станций. Все более дешевыми и доступными становятся устройства хранения данных большой емкости и спутнико- вые системы передачи информации. Это времени за «электромагнитным дыхани-позволит в ближайшее время создать гло- ем» Земли.

бальные системы мониторинга в реальном