Улучшение обнаружения мошенничества с банковскими картами с помощью квантовых вычислений

Обнаружение мошенничества с банковскими картами является важнейшей задачей в современной финансовой экосистеме. Традиционные системы обнаружения мошенничества, которые обычно полагаются на алгоритмы машинного обучения, статистическое обнаружение аномалий или подходы на основе правил, сталкиваются со значительными ограничениями при работе с большими объемами данных транзакций, нелинейными отношениями между различными характеристиками транзакций и всё более сложными методами мошенничества [1]. Традиционным системам всё труднее обнаружить сложные закономерности мошеннического поведения в режиме реального времени, что приводит к ложным срабатываниям (необоснованное оповещение о мошенничестве) либо необнаружению мошенничества.

Квантовые вычисления ( Quantum computing ) с их способностью обрабатывать информацию способами, принципиально отличными от классических систем, предлагают многообещающий путь для решения этих проблем [2]. Квантовая механика делает возможными такие явления, как суперпозиция (superposition) и запутанность (entanglement), которые позволяют квантовым системам исследовать несколько возможностей одновременно и моделировать сложные взаимодействия более эффективно. Используя эти возможности, квантовые вычисления могут обеспечить преобразующий подход к обнаружению мошенничества с банковскими картами.

В статье представлена новая квантовая методология обнаружения мошенничества в транзакциях по банковским картам – Quantum Transaction Flow Analysis (QTFA) . QTFA использует квантовые сети для моделирования потока транзакций и выявления аномалий, которые могут указывать на мошенническую деятельность. Используя квантовую механику для представления сложных взаимосвязей между транзакциями, QTFA предлагает более точную, масштабируемую и работающую в режиме реального времени альтернативу традиционным системам обнаружения мошенничества.

В статье дается всестороннее описание QTFA, ее теоретической основы, математической формулировки. Кроме того, показано, как QTFA можно применять для обнаружения мошенничества в реальном мире, иллюстрируя ее потенциал для повышения эффективности и результативности систем обнаружения мошенничества в финансовом секторе.

Связанные исследования

Обнаружение мошенничества с банковскими картами было тщательно изучено, что привело к разработке многочисленных методов, призванных бороться с меняющейся

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год природой мошеннической деятельности. Классические подходы на основе правил и статистических методов легли в основу механизмов раннего обнаружения. Эти системы полагались на фиксированные пороговые значения и предопределенные правила для выявления аномалий в шаблонах транзакций. Однако они с трудом приспосабливались к динамическим стратегиям, используемым мошенниками, что часто приводило к высоким показателям ложных срабатываний и ограничению масштабируемости. Позднее применение методов машинного обучения стало более распространенным при обнаружении мошенничества; использовались такие алгоритмы, как деревья решений, случайные леса и машины опорных векторов. Эти методы анализируют большие объемы исторических данных транзакций для изучения шаблонов, указывающих на мошенническую деятельность. Кроме того, модели глубокого обучения, включая рекуррентные нейронные сети (RNN) и сверточные нейронные сети (CNN), продемонстрировали особый успех в выявлении временных и пространственных связей в данных транзакций [3]. Несмотря на эти достижения, эти методы сталкиваются с проблемами интерпретируемости и вычислительной эффективности, особенно при применении к несбалансированным наборам данных или крупномасштабным сетям транзакций [4].

Квантовые вычисления стали многообещающей альтернативой для преодоления ограничений классических методов [5]. Недавние исследования посвящены использованию алгоритмов квантового машинного обучения, таких как квантовые машины опорных векторов (QSVM) и квантовые нейронные сети (QNN), для решения проблем масштабируемости и повышения скорости вычислений [6].

В статье предложен инновационный метод Quantum Transaction Flow Analysis (QTFA) в качестве нового решения для обнаружения мошенничества с банковскими картами.

Методология

Методология квантового анализа потока транзакций (Quantum Transaction Flow Analysis – QTFA) предоставляет инновационную структуру для решения растущей проблемы обнаружения мошенничества с банковскими картами путем интеграции принципов квантовых вычислений. QTFA моделирует транзакции как квантовые состояния, позволяя им существовать в суперпозиции законного и мошеннического поведения. Такое представление обеспечивает многомерный анализ, который недостижим с помощью классических систем. Кодируя отдельные транзакции как квантовые состояния и связные транзакции посредством квантовой запутанности, QTFA раскрывает скрытые связи и закономерности, указывающие на мошенническую деятельность. Этот подход динамического моделирования обеспечивает адаптивность к меняющимся тенденциям мошенничества в реальном времени.

Структура использует сеть квантового потока для захвата и анализа взаимозависимо-стей между транзакциями. Узлы в сети представляют отдельные транзакции, в то время как взвешенные ребра (weighted edges) обозначают такие связи, как общие идентификаторы или временная близость. Эти веса помогают расставить приоритеты связей для более глубокого анализа. Вся сеть развивается с течением времени, управляемая унитарными операторами, которые включают ожидаемое поведение, полученное из исторических данных. Эта временная эволюция является ключом к обнаружению сложных схем мошенничества, которые используют уязвимости сети.

Оптимизация играет решающую роль в уточнении структуры сети, где используется алгоритм квантовой аппроксимации оптимизации (Quantum Approximate Optimization

Улучшение обнаружения мошенничества с банковскими картами с помощью квантовых вычислений

Algorithm – QAOA) [7]. Этот гибридный алгоритм итеративно оптимизирует сеть, настраивая параметры, которые минимизируют расхождения между наблюдаемыми и ожидаемыми потоками транзакций. Чередуя квантовые и классические вычислительные слои, QAOA обеспечивает эффективное и точное представление нормального поведения транзакций, позволяя эффективно отмечать отклонения. Наконец, QTFA обнаруживает аномалии с помощью квантовых измерений, сворачивая состояния транзакций в окончательные классификации законных или мошеннических. Этот процесс также учитывает контекстную динамику транзакций, такую как географическое положение или время возникновения, с помощью адаптивных механизмов пороговой обработки. Кроме того, квантовая запутанность еще больше усиливает обнаружение, анализируя корреляции между отмеченными транзакциями, позволяя идентифицировать скоординированные мошеннические схемы. Вместе эти компоненты позиционируют QTFA как преобразующее решение для борьбы с финансовым мошенничеством с беспрецедентной точностью и масштабируемостью.

Имплементация QTFA

Имплементация квантового анализа потока транзакций (QTFA) включает несколько взаимосвязанных этапов, начиная с предварительной обработки данных транзакций, за которыми следует построение квантовой схемы (Quantum circuit) для представления сети потока транзакций. Процесс продолжается применением QAOA (Quantum Approximate Optimization Algorithm) для оптимизации сети и завершается обнаружением аномалий с помощью квантовых измерений.

Предварительная обработка данных

Предварительная обработка данных (Data Preprocessing) транзакций имеет решающее значение для подготовки данных к кодированию в квантовые состояния. Во-первых, необработанные данные проходят тщательную очистку для устранения потенциальных несоответствий, пропущенных значений и шума. Учитывая неоднородную природу наборов данных для обнаружения мошенничества, поступающих из разных источников, таких как платежные системы и платформы электронной коммерции, гармонизация данных имеет решающее значение. Это включает стандартизацию форматов атрибутов с учетом различных масштабов и типов встречающихся данных.

Второй шаг включает нормализацию. Нормализация имеет первостепенное значение для обеспечения того, чтобы каждый атрибут вносил пропорциональный вклад в последующий процесс кодирования квантового состояния. Без нормализации атрибуты с большими масштабами могут непропорционально влиять на квантовое представление, потенциально искажая результаты. Масштабирование всех атрибутов до общего диапазона (например, [0, 1]) позволяет сохранить их относительную важность, совместимость со схемами квантового кодирования. Кроме того, для повышения эффективности применяются методы отбора признаков и снижения размерности, такие как анализ главных компонент (PCA) [8]. Вычислительная сложность снижается за счет выявления и сохранения только наиболее релевантных и информативных атрибутов, что является критическим фактором, учитывая ограничения ресурсов текущего квантового оборудования.

Наконец, предварительно обработанные данные кодируются в квантовое состояние. Амплитудное кодирование отображает атрибуты каждой транзакции на амплиту-

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год ды вектора квантового состояния. Этот подход предлагает компактное и эффективное представление многомерных данных, минимизируя требования к памяти по сравнению с классическими представлениями. Для этой работы используются фреймворки квантового программного обеспечения (Qiskit) для построения этих квантовых состояний на квантовых симуляторах, а затем на реальном квантовом оборудовании.

Построение Quantum Circuit

Quantum circuit (Квантовая схема) образует основу QTFA, представляя сеть потока транзакций в квантовом состоянии. Каждая транзакция отображается на кубит, а отношения между транзакциями, такие как временная близость или сходство в моделях расходов, кодируются с помощью запутывания (entanglement). Первоначально все кубиты помещаются в состояние суперпозиции с использованием Hadamard gates, представленных математически как | ^ 0 ) = H ® ⁿ | 0 ) ® n , где n - количество транзакций, а H обозначает Hadamard gate.

Атрибуты транзакций кодируются в амплитуды квантового состояния с использованием параметризованных вентилей вращения (parameterized rotation gates). Например, вентиль R _y(θ), который вращает состояние кубита на угол θ, определяется как cos ( 0 /2 ) - sin ( 0 / sin ( 0 /2 )    cos ( 0 /2 )

R y ( 0)

Угол θ вычисляется на основе нормализованных атрибутов каждой транзакции. Для моделирования отношений между транзакциями вводится запутанность с использованием controlled-NOT gates . Для транзакций с сильными корреляциями создается запутанное состояние | ^ _entangled ) = 1/^2 (|00 ) + |11 ) ), гарантируя, что состояние одного кубита влияет на другой.

Оптимизация квантового потока с помощью QAOA

Для оптимизации сети потока транзакций и выявления аномалий QTFA использует алгоритм приближенной квантовой оптимизации (QAOA). Этот подход попеременно применяет Cost Hamiltonian ( H _C) и Мixing Hamiltonian ( H _M) для итеративного уточнения квантового состояния. Cost Hamiltonian (стоимостной гамильтониан) кодирует цель минимизации отклонений между наблюдаемыми и ожидаемыми потоками транзакций:

HC ^^(fe fxxpcttd) , ее E где fe – наблюдаемый поток на ребре e; fexpected – ожидаемый поток, полученный из истори- ческих данных.

Мixing Hamiltonian (Смешивающий гамильтониан), HM = ∑i=1nXi, где Xi – оператор Pauli-X, примененный к i-му кубиту, исследует пространство решений. Квантовое состоя- ние развивается посредством чередующихся слоев этих гамильтонианов, выражаемых как: p

I^ p} = П e "H^HM e ^Y ‘H C 1^ 0 ,

= 1

где p – количество слоев; β l , γ l – параметры, оптимизированные с использованием классических методов.

Этот итеративный процесс создает оптимизированное квантовое состояние, которое отражает сеть потока транзакций.

Улучшение обнаружения мошенничества с банковскими картами с помощью квантовых вычислений

График сходимости целевой функции (см. Рисунок 1) демонстрирует, как алгоритм квантовой приближенной оптимизации (QAOA) оптимизирует целевую функцию по итерациям. Он показывает тенденцию к снижению значения цели, отражающую сходимость алгоритма.

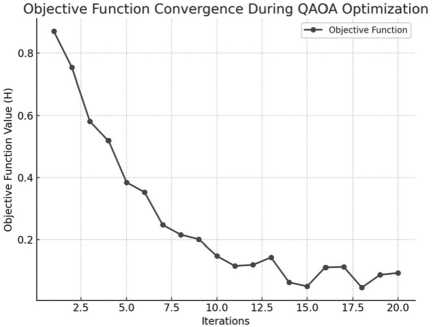
Рисунок 1. График сходимости целевой функции Источник: выполнено автором.

Квантовое измерение и обнаружение аномалий

В рамках QTFA квантовое измерение имеет основополагающее значение для обнаружения аномалий в сети транзакционного потока. Наблюдая квантовое состояние системы, структура сворачивает суперпозицию состояния в определенный результат, что позволяет точно идентифицировать транзакционные шаблоны. Каждая транзакция представлена квантовым состоянием | ψ 〉 , где вероятность мошенничества выводится из квадрата амплитуды мошеннического компонента состояния. Вероятность P (fraud) вычисляется как

P(fraud)= | 〈 fraud | ψ 〉 | ²

Здесь | 〈 fraud | ψ 〉 | представляет собой внутренний продукт между измеренным состоянием и состоянием мошенничества. Аномалии выявляются, когда P(fraud) превышает предопределенный порог θ_fraud, такой, что

P (fraud) > θ_fraud.

Этот порог (threshold) динамически корректируется на основе исторических данных и информации в реальном времени, обеспечивая адаптивность к меняющимся схемам мошенничества. Если пороговое условие выполняется, транзакция помечается как потенциально мошенническая, что позволяет проводить целенаправленное расследование. Постоянно сравнивая измеренные состояния с ожидаемыми нормами, закодированными в исторических данных, QTFA минимизирует ложные срабатывания и поддерживает высокую чувствительность к аномалиям, обеспечивая точное и эффективное обнаружение мошенничества.

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год

Результаты

Экспериментальная установка

Экспериментальная установка включала набор данных, включающий 1 млн транзакций по банковским картам, из которых 1 % был помечен как мошеннический, что отражает реальные дисбалансы в сценариях обнаружения мошенничества. Каждая транзакция характеризовалась такими признаками, как сумма транзакции, категория продавца, географическое местоположение, временная метка и поведение держателя карты и др. Признаки были предварительно обработаны с помощью нормализации и закодированы в квантовые состояния, что позволило представить их в сети потока квантовых транзакций. Эксперименты проводились на гибридной квантово-классической архитектуре. Квантовые вычисления выполнялись с использованием фреймворка Qiskit от IBM Quantum, с использованием 5-кубитного квантового аппаратного бэкэнда и симулятора вектора состояния для оптимизации и выполнения схемы [9]. Симулятор Aer от Qiskit обеспечил надежную среду тестирования, а его интеграция с оборудованием IBM Quantum позволила осуществить потенциальное развертывание на реальных квантовых устройствах. Классические вычисления и сравнения моделей проводились на машине, оснащенной процессором Intel i9, 64 ГБ оперативной памяти и графическим процессором NVIDIA RTX 3080. Для оптимизации потоков транзакций использовался алгоритм приближенной квантовой оптимизации (QAOA), а для обнаружения аномалий применялись квантовые методы измерения.

Полученные результаты

Результаты подхода квантового анализа потока транзакций (QTFA) демонстрируют его замечательную эффективность в повышении обнаружения мошенничества с банковскими картами. QTFA достиг точности (аccuracy) 98 %, что значительно превосходит традиционные модели машинного обучения, такие как случайные леса (92 %) и опорные векторные машины (SVM, 89 %) (см. Рисунок 2). Такой высокий уровень точности подчеркивает способность QTFA улавливать сложные закономерности в транзакционных данных, которые классические методы могут упустить из виду.

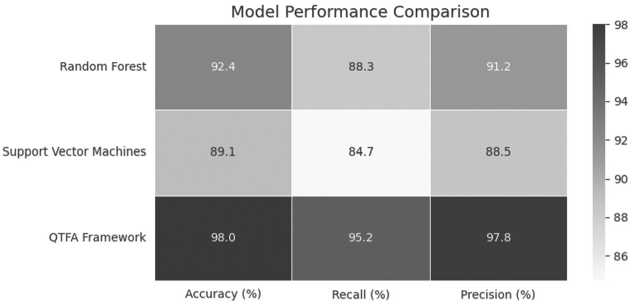
Рисунок 2. Полученные результаты.

Источник: выполнено автором.

Улучшение обнаружения мошенничества с банковскими картами с помощью квантовых вычислений

С точки зрения Precision QTFA достиг 97 %, что значительно выше точности случайных лесов (91 %) и SVM (88 %). Эта метрика отражает способность QTFA минимизировать ложные тревоги за счет точного определения мошеннических транзакций. Кроме того, QTFA достиг Полноты ( Recall ) в 95 %, превзойдя случайные леса (88 %) и SVM (84 %). Это указывает на эффективность QTFA в обнаружении реальных случаев мошенничества, даже в сценариях, где мошенническая деятельность составляет всего 1 % от набора данных. Еще одним важным показателем является уровень ложных срабатываний (False Positive Rate – FPR). QTFA снизил FPR на 10 % по сравнению с базовыми моделями (см. Таблицу). Это снижение подчеркивает его преимущество в сокращении количества законных транзакций, помеченных как мошеннические, минимизируя сбои для настоящих пользователей. Несмотря на свою превосходную точность и правильность, QTFA продемонстрировал более длительное время выполнения на больших наборах данных из-за вычислительных затрат на обработку квантовой схемы. Напротив, случайные леса и SVM, хотя они и быстрее, не смогли сравниться с производительностью обнаружения мошенничества QTFA.

Результаты подчеркивают потенциал QTFA для революции в обнаружении мошенничества путем использования квантовых принципов для выявления тонких аномалий транзакций. Сравнительный анализ, обобщенный в Таблице, дает дополнительную ясность относительно преимуществ QTFA перед традиционными методами. Это сравнение подчеркивает значительные преимущества QTFA по сравнению с классическими подходами, особенно с точки зрения точности, отзыва и общей точности. Хотя QTFA требует больших вычислительных ресурсов, его улучшенные показатели производительности оправдывают его применение, особенно в сценариях, где минимизация ложных срабатываний и обнаружение тонких схем мошенничества имеют первостепенное значение. Выводы, полученные из этих результатов, обеспечивают прочную основу для потенциального внедрения QTFA в реальные системы обнаружения мошенничества.

Таблица

Сравнение по параметрам FPR и Время выполнения моделей

Model	False Positive Rate (%)	Execution Time (s)
Random Forest	10	45
Support Vector Machines	13	40
QTFA Framework	5	150

Источник: составлено автором.

Интеграция QTFA в реальные системы

Интеграция QTFA в реальные системы представляет собой важнейший шаг вперед в области обнаружения мошенничества с банковскими картами. Для обеспечения бесперебойного развертывания QTFA можно внедрить в существующие финансовые инфраструктуры в качестве дополнительного уровня, наряду с классическими моделями обнаружения мошенничества. Процесс начинается с приема данных о транзакциях из различных источников, таких как платежные шлюзы, системы точек продаж и онлайн-платфор-мы. Эти данные проходят предварительную обработку для обеспечения совместимости с требованиями квантовых вычислений, включая кодирование признаков и нормализа-

Вестник Российского нового университета

Серия «Сложные системы: модели, анализ и управление», выпуск 1 за 2025 год цию. После подготовки данные транзакций передаются в гибридную структуру, включающую как квантовые, так и классические компоненты. Квантовый уровень использует QTFA для моделирования потоков транзакций как квантовых состояний, применяя такие принципы, как суперпозиция и запутанность, для обнаружения тонких схем мошенничества. В то же время классический уровень выполняет параллельный анализ для проверки квантовых результатов, обеспечивая надежность и интерпретируемость. Окончательный результат, включающий оценки вероятности мошенничества и отмеченные аномалии, интегрируется в панель управления, доступную пользователю. Эта панель мониторинга предоставляет аналитику в режиме реального времени, позволяя финансовым учреждениям принимать оперативные и обоснованные меры против потенциальных мошеннических действий.

QTFA имеет потенциал революционного обнаружения мошенничества, устраняя критические ограничения классических подходов. Традиционные модели часто дают сбои при столкновении с крупномасштабными наборами данных или высокодинамичными схемами мошенничества. Напротив, способность QTFA обрабатывать огромные объемы данных и исследовать несколько сценариев одновременно обеспечивает большую точность и масштабируемость. Кроме того, квантовые методы оптимизации, такие как алгоритм приближенной квантовой оптимизации (QAOA), повышают способность системы выявлять сложные корреляции и аномалии, которые классические алгоритмы могут упустить из виду. Уменьшая ложные срабатывания и улучшая показатели полноты (recall), QTFA минимизирует эксплуатационные расходы и улучшает пользовательский опыт.

Обсуждение

Экспериментальные результаты подчеркивают эффективность QTFA в улучшении обнаружения мошенничества с банковскими картами. Используя квантовые принципы, такие как суперпозиция и запутанность, QTFA обеспечил комплексное представление сетей транзакций, что позволило обнаружить сложные и скрытые схемы мошенничества. Интеграция QAOA позволила эффективно оптимизировать сеть потока транзакций, способствуя обнаружению аномалий с удивительной точностью. Важнейшим преимуществом QTFA была его способность уменьшать ложные срабатывания, устраняя основное ограничение традиционных моделей [10]. Это улучшение не только улучшает пользовательский опыт, сводя к минимуму сбои для законных владельцев карт, но и снижает операционные расходы для финансовых учреждений. Кроме того, производительность QTFA на несбалансированных наборах данных подчеркивает его адаптивность к реальным сценариям, где мошеннические транзакции составляют небольшую часть от общего объема данных. Однако эксперименты также выявили проблемы. Время выполнения QTFA увеличивалось с размером набора данных, указывая на то, что текущее квантовое оборудование является узким местом для крупномасштабных приложений. Кроме того, необходимость надежного кодирования данных и зависимость от гибридных квантовоклассических архитектур усложняют развертывание. Будущая работа должна быть сосредоточена на преодолении этих проблем путем изучения передового квантового оборудования, эффективных схем кодирования и методов параллельной обработки. Включение динамических возможностей обнаружения мошенничества и анализа в реальном времени еще больше повысит практичность QTFA.

Улучшение обнаружения мошенничества с банковскими картами с помощью квантовых вычислений

Заключение

Метод анализа потока квантовых транзакций (QTFA) представляет собой новаторский подход к обнаружению мошенничества с банковскими картами, используя уникальные преимущества квантовых вычислений. Результаты показывают, что QTFA может достигать превосходной точности и снижать показатели ложноположительных результатов по сравнению с классическими методами, что делает его многообещающим решением для борьбы с современными схемами мошенничества. Интеграция квантовых принципов, таких как суперпозиция и запутанность, позволяет QTFA обнаруживать тонкие и скрытые закономерности в данных транзакций. Используя QAOA для оптимизации потока, метод адаптируется к динамической природе мошеннических действий, предоставляя масштабируемую и надежную структуру для обнаружения мошенничества. В то время как QTFA демонстрирует значительные достижения, ограничения текущего квантового оборудования и сложность гибридных реализаций подчеркивают области для улучшения. Будущие исследования должны отдавать приоритет разработке масштабируемых квантовых архитектур, эффективных методов кодирования данных и механизмов обнаружения мошенничества в реальном времени, чтобы полностью реализовать потенциал QTFA в реальных финансовых системах. Это исследование подчеркивает преобразующее влияние квантовых вычислений на финансовые приложения, прокладывая путь для инноваций в решении проблем современного обнаружения мошенничества.