Улучшение управления в одном классе систем с линейным неограниченным управлением

Введение. Постановка задачи

Различные итерационные методы улучшения управляемых процессов –– обширная область исследований и разработок в теории оптимального управления, нацеленных на эффективное решение практических задач. Исторически развитие этих методов началось одновременно с созданием современной теории оптимального управления.

Метод глобального последовательного улучшения управления был предложен и получил дальнейшее развитие в [1 –4] и ряде других работ. Этот метод обладает рядом преимуществ перед широко применяемыми методами локального улучшения процессов (например, отсутствием настроечных коэффициентов, меньшей зависимостью от начального приближения, реализацией посредством единственной пары прогонок и др.).

В работе рассматривается применение метода глобального улучшения к решению класса задач оптимального управления

• (1)           x = f (t,x)+( -D D ) ux, t e [t o ,t F ],

  Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 09-01-00170-а).

• (2)    x(t o ) = x o ,

• (3)    F № )) ^ min,

где D — диагональная невырожденная n x n матрица с элементами d ¹ ,..., d ⁿ e R ¹ на главной диагонали. Здесь x(t) е R ²ⁿ — непрерывная, кусочно-гладкая фазовая траектория, u(t) е R 1 — кусочнонепрерывное неограниченное управление.

Задача улучшения управления в задаче (1) – (3) состоит в следующем. Пусть задана допустимая пара (x I (t),u I (t)). Требуется найти допустимую пару (x II (t),u ⁿ (t)), для которой справедливо неравенство F (x II (t F )) <  F (x I (t F )). Решая эту задачу итерационно, можно получить улучшающую, в частности, минимизирующую последовательность { x s (t), u s (t) } . Однако, применение численных итерационных методов улучшения (например, метода глобального улучшения Кротова) затрудняют отсутствие ограничений на управление и проблема выбора начального управления u(t). На практике приходится ставить и затем варьировать в многочисленных вычислительных экспериментах принудительное ограничение на управление (например, в виде | u(t) | <  const) и начальное управление.

Особенностью класса задач (1) – (3) является возможность явного преобразования исходной задачи улучшения к задаче улучшения управления для системы меньшей размерности с ограниченным управлением, что позволяет осуществить аналитически или с помощью итерационных методов улучшения управления поиск качественного начального приближения для исходной задачи улучшения.

• 1.    Преобразование к системе с ограниченным управлением

Воспользуемся методом преобразования исходной системы к производной [5, 6], который позволяет свести задачу улучшения начального управления для системы (1) к производной задаче меньшего порядка. Для этого найдем y = n(t,x) = (п1,■■■, П2п-1) — совокупность независимых первых интегралов системы дифференциальных уравнений dx   / 0   D \

— =           x.

dT   \ — D 0

Имеем yi = ni(x) = (xi)2 + (xn+i)2, i = t;^, п+1      1           xj + 1     1         x1     ■    1-------T

У ^+j = d j +1 ^arccos y j +i - d i ^arccos y i , j = 1,n - ¹

Тогда с помощью замены переменных x1 = x1(y, 6) = py1 cos(d10), xn+1 = xn +1(y, 6) = py1 sin^1#), xi = xi(y,6) = pyicos (di(6 + yn+i 1)) ,   6 e [—n,n], xn+i = xn+i(y, 6) = pyisin (di(6 + yn+i-1^ , i = 2, n,

исходная задача (1)–(3) переходит в задачу для производной системы y = g(t,y,6), t e [to,tF], y e R2n-1, 6 e [-n,n],

• ⁽⁴⁾                y(t o ) = n(x(t o )),

^{F (} y ^{( t} F )) = ^min F ^{( x (} y ^{( t} F ^{) ,6 ))} ^ ^min, ee [ -n,n ]

где 6(t) — кусочно-непрерывное управление, g1(t,y, 6) = 2РУ1 (f 1(t,x(y, 6))cos(d16) + fn+1(t,x(y,6))sin(d16)) , gj+1(t, У, 6) = 2Pyj+1 f.f j+1(t, x(y, 6)) cos (dj+1(6 + yn+j)) + +f n+j+1(t, x(y, 6)) sin (dj+1(6 + yn+j)) ), n+j (t   6) = f n+j+1(t, x(y, 6)) cos (dj+1 (6 + yn+j)) - g V,y’ ’              dj^1py+

-f ^j+1 (t, x(y, 6)) sin ( d ^j+1 (6 + y n ^+j ) ) d j ⁺¹ py ^j+1

f ⁿ⁺¹ (t,x(y,6))cos(d ¹ 6) - f ¹ (t,x(y,6))sin(d ¹ 6)    .  ------_r

--=---------------------, i = 1, n — 1.

d 1 py 1

Если присоединить уравнение f n+1(t,x(y,6))cos(d16) — f 1(t,x(y,6))sin(d16)

• ^{(5)     6} =-------------------- ;r"7^ --u,

• 2.    Улучшение управления для квантовых систем

с начальным условием 6(t o ) = 6 o (x o ), то получится представление исходной системы в новых фазовых переменных у ¹ ,..., y ^2n-1 , 6 вместо прежних x ¹ ,..., x ²ⁿ .

Для решения полученной задачи улучшения управления можно воспользоваться методом глобального улучшения [7]. А именно, для начального допустимого процесса (yI(t),9I(t)) найдем

Найдем функцию 9(t,y) согласно формуле

9(t, y) = arg max (^ T g(t, y, 9) + v 0 ) . θ ∈ [ -π,π ] ^y

Замкнув полученной функцией управляемую систему (4) , найдем улучшенный допустимый процесс (y II (t),9 ⁿ (t) . Повторим шаги алгоритма.

Для задачи улучшения (1) – (3) в качестве начального приближения можно выбрать аппроксимацию полученного процесса (y II (t), 9 II (t) с помощью допустимых процессов исходной задачи (1) - (3) [6] . При этом может оказаться весьма полезным ранее отброшенное уравнение (5) , выражающее связь управления u(t) в исходной системе и управления 9(t) в производной системе.

К рассматриваемому классу задач относятся актуальные квантовые системы с управлением [3, 4] . Для них система (1) имеет компактное представление в виде комплексного уравнения, представляющего собой конечномерный аналог основного уравнения квантовой механики (уравнения Шредингера в частных производных)

Ш = 1Нш, где I — мнимая единица, H = H1 + IH2 — комплексный линейный самосопряженный оператор, ш = а + ip — комплексный вектор фазовых переменных, α, β ∈ Rn . Выделяя в этом уравнении вещественную и мнимую часть, получаем систему а = —Н2а — Н1в, в = Н1а - Н2в.

При H 1 = - Pa — иР в , где Pa , Pb — произвольные симметричные матрицы, u(t) е R ¹ , H 2 = 0 эта система имеет вид управляемой гамильтоновой системы

• (6)            cn = ( Pa + иР в )в, в = — ( Pa + иР в )а.

Система (6) имеет динамический инвариант f (ш) = к|ш^2 = как2 + квк2 = аТ а + в T в = const, т. е. все траектрии системы (6), независимо от выбора управления u(t), расположены на сфере с центром в начале координат (для любого допустимого u(t) справедливо k|^(tF)k = k|^(to)^).

Поставим задачу улучшения управления для гамильтоновой системы (6) , обозначив z = (z ¹ , .. ., z ²ⁿ ) = (a ¹ ,. .. , a n , в 1 , ... , в ^п ),

z =

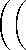
- P A

P A

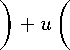
- P B

P B

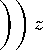
t G [t o , t F ],

z ( t 0 ) = z 0 ,

F o (z(t F )) ^ min.

Так как для симметрической матрицы P B существует невырожденная матрица M , приводящая ее к диагональному виду

M-1PB M = D, то система (7) может быть приведена к системе (1) с помощью ли-

нейного невырожденного преобразования z = Mx =

-~'

M

,—-

M

x .

Тем самым показано, что задача улучшения управления (7) – (9)

эквивалентна задаче улучшения управления (10)

/                          -——' -     -——' \/

0     M-1PAM0

X —x

-M-1PA M 0

~

D

ux

t G [t o ,t F ],

x ( t 0 ) = x 0 ,

• (12)                F (x(t _F )) = F ₀ (Mx(t F )) ^ min,

  или, что тоже самое, эквивалентна задаче улучшения управления

  
  

  (1) - (3) при f (t,x) =

  
  

  -~' -    -~'

  - M ^-1 P A M

  
  

  ,—-       ,—-

  M - 1 P _A M

  e

  
  

  x . Без ограничения

  
  

  общности можем считать, что матрица D невырождена (в противном

  
  

• 3.    Примеры

случае рассматривали бы систему меньшего порядка).

Пример 1. Рассмотрим задачу оптимального управления (10) –

/ 0 0

0 0

0 b b 0

• (12)    при P B = E n , т.е. d i = 1, i = 1,n, P A b G R ¹ .

  0 b b 0

  
  

  0 0 00

  
  

C помощью замены переменных xi = xi(y, 9), i = 1, 2n, предло- женной в п. 2, с учетом справедливости равенств f i(t, x) = bx2n-i+1, f n+i(t, x) = -bxn-i+1,   i = 1, n, рассматриваемая задача оптимального управления переходит в задачу оптимального управления для производной системы (4), где g1 (t,y,9 = 2bpy1yn sin y2n-1, gi+1(t, y, 9) = 2b Vyi+yn- sin(y2n-i-1 - yn+i), i = 1, n - 2, gn(t,y,9) = -2bVyIyn sin y2n-1, n-i                                n gn+i(t, y, 9) = -bWy^+T cos(y2n-i-1 - yn+i) + b^ cos y2n-1, g2n-1(t,y,9) = b Ly^- - Sy1! cos y2n-1. y1      yn

Поскольку выражения для g фактически не зависят от θ , то производная система становится неуправляемой, и исходная задача вырождается в задачу минимизации функции одной переменной

F ( x (W f ),9)) ^ min , ec [ -n,n ]

где y(t) — решение задачи Коши yj = g(y), y(t0) = n(x(t0)), t G [tQ/tF]•

Обозначим 0f = arg min F (x(y(t F ), 0)), тогда исходная задача оп- θ ∈ [ -π,π ]

тимального управления сводится к поиску функции u(t), обеспечивающей существование функции 0(t), которая подчинена системе ра- венств

0(t) = — bJy^cosy 2 ^{n 1} - u(t), t E [t o ,t F ], y ¹ ( t )

0(t o ) = 0 0 = 0 o (x o ), 0(t F ) = 0 f , 0(t) E [ — —,—].

Таких функций u(t) очевидно бесконечно много. Выберем одну из них посредством выбора функции 0(t), а именно, положим

0(t) =

θ - θ

F----0t + tF - t0

θ 0 t F - θ F t 0 t _F - t ₀

Тогда функцию u(t), доставляющую минимум функционалу F(x(tF)), можно взять в виде

/e ^{n (t)}    ~2 п-1 ⁰F ^{— 0} О

u(t) = — b         cos y ¹ .

у e 1 (t)               t F — to

Например, решим задачу оптимального управления при n = 2, b = 1, t0 = 0, x(t0) = (1,1, 0, 0)T, F (x(tF)) = x1(tF)x2(tF) ^ min. В этом случае для определения функции y(t) следует решить задачу Коши y1 = 2 Уy1y2 sin y3, y2 = —2 Уy1 y2 sin y3, y 3=(q|1 - q^)cos y3,

y(0) = (1,1,0) ^T .

Получим y ¹ (t) = 1, y 2 (t) = 1, y 3 (t) = 0. Найдем 0 0 = 0 и 0 _F :

0 _F = arg min F (x(y(t _F ),0)) = θ ∈ [ -π,π ]

= arg min У у ¹ (t F ) cos 0yy ² (t _F ) sin(0 + y ³ (t F )) = θ ∈ [ -π,π ]

arg min cos ² 0 = ± — .

06 [ —n,n ]               2

Положим для определенности 0f = n, тогда функцию u(t), доставляющую минимум функционалу F(x(tF)) равный 0, можно взять в виде

u(t) =

π

2t F

Пример 2. Рассмотрим задачу (10) - (12) при d ¹ = — 1, d i = 1, i =

2, n, т. е. P B =

— 1 0

0       =

, P A

E n- 1

/

0 0

.

.

.

0 b

0   ...   0   b\

0    ...    b0

.      ..       .      .       , b G

.

C помощью замены переменных x i =

женной в п. 2, с учетом справедливости равенств

b ... 00

0 ... 00

x i (y,0), i = 1, 2n, предло-

f i(t, x) = bx2n-i+1, f n+i(t, x) = — bxn-i+1,   i = 1, n, рассматриваемая задача оптимального управления переходит в задачу оптимального управления для производной системы (4), где g1(t,y,0) = 2bVyV sin(20 + y2n-1), gi+1(t,y,y) = 2bVyi+1yn i sin(y2n i 1 — yn+i),   i = 1,n — 2, gn(t, y, 0) = — 2bVy1yn sin(20 + y2n-1), n-i gn+i(t, y, 0) = —bJ — cos(y2n-i-1

— y n + i ) — b^y ! cos(20 + y ^2n-1 ),

g ^2n-1 (t,y,0) = —b

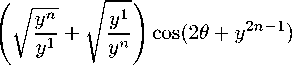
Здесь отброшено уравнение с начальным условием

0 = by yr cos(20 + y2n 1) — u, 0(to) = 00 = 0o(xo), которое может оказаться полезным при восстановлении управления u(t) для исходной задачи оптимального управления по найденному решению задачи оптимального управления для производной системы.

Например, решим задачу улучшения начального управления u I (t) = 0 при n = 3, b = 1, t ₀ = 0, t _F = 0.25,

x(t o ) = (1,1,1,0, 0, 0) T , x . = (0,1,1,1, 0, 0) T ,

F (x(t _F )) = (x(t _F ) — x * ) T (x(t _F ) — x * (t _F )) ^ min, т. е. задачу минимизации расстояния до заданной точки x _∗ . Преобразуем функционал с учетом инварианта рассматриваемой системы:

F (x(t _F )) = x ^T (t _F )x(t _F ) + x T x * — 2x ^T (t _F )x * =6 — 2x ^T (t _F )x * .

Попробуем решить задачу улучшения численно с помощью глобального алгоритма улучшения Кротова [7] двумя различными способами.

Способ 1. Применим алгоритм глобального улучшения непосредственно к исходной задаче, поставив принудительно ограничения на управления, например в виде u(t) е [ - 10; 10], при приближении разрещающей функции ф ⁰ (^х) с помощью полиномов первого порядка.

Способ 2. Применим алгоритм глобального улучшения к производной задаче, соответствующей исходной задаче, y1 = 2 VУ1 У3 sin(29 + y5), t е [0,tF], y2 = 0, 9 е [—п,п], y3 = —2py1y3 sin(29 + y5), y 4 = —1 — qyl cos(29 + y5), y5=- cos(29+y5) (qyi+qy3),

y(0) = (1,1,1,0,0) T ,

F (y(t F )) = min F (x(y(t F ),9)) ^ min, θ ∈ [ -π,π ]

при приближении разрещающей функции ф ⁰ (t, y) с помощью полиномов второго порядка. Начальному управлению u I (t) = 0 здесь соответствует начальное управление 9 I (t) = t. На улучшенном управлении 9 II (t) значение функционала составило F Уу¹¹ (2.5)) = — 2.94465. Далее с помощью ранее отброшенного уравнения

9 = ^У1 cos(29 + у5) — и, а точнее, с помощью его разностного аналога

u(t) = — ^{9(t +} hh ^{— 9 ( t )} + ^cos(29(t) + y « ( _t )).

построим начальное управление uI (t) для итерационной процедуры улучшения в исходной задаче, поставив ограничения на управления, например в виде u(t) е

min u I (t), max u I (t)

(в нашем случае

t ∈ [ t 0 ,t F ]            t ∈ [ t 0 ,t F ]

u(t) е [0; 30]), при приближении разрещающей функции ф0(t,x) с помощью полиномов первого порядка.

Полученные значения функционала на первых девяти итерациях алгоритма представлены в следующей таблице:

Номер итерации	Значение F(x(t F )) (способ 1)	Значение F (x(t F )) (способ 2)
0	5.20076	5.96956
1	0.72426	0.01352
3	0.32999	0.00943
5	0.18185	0.00876
7	0.10929	0.00845
9	0.08214	0.00826

Из таблицы видно, что второй способ решения позволил уже на первой итерации алгортма глобального улучшения получить значение функционала меньшее, чем при первом способе решения, и существенно улучшить значение функционала на последующих итерациях. На рис. 1 представлены графики улучшенного управления (на девятой итерации алгоритма глобального улучшения) при расчете по способу 1 (черная линия) и по способу 2 (красная линия). Соответствующие траектории представлены на рис. 2 и 3 соответственно для способа 1 и способа 2.

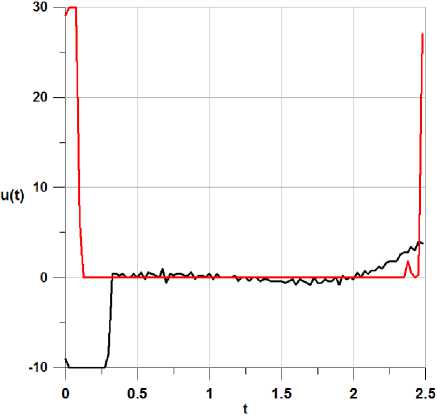
Рис. 1.

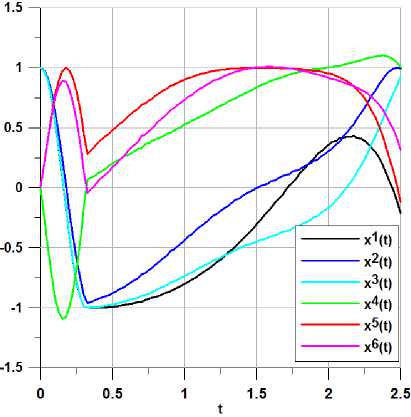
Рис. 2.

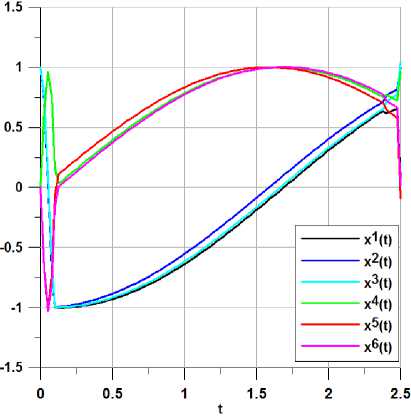
Рис. 3.

Заключение

На основании полученных результатов можно заключить, что предложенный алгоритм, построенный на основе общего метода Кротова глобального улучшения управления, служит хорошим инструментом для численного решения задач улучшения рассматриваемого класса. При этом переход к производной системе обеспечивает высокую эффективность поиска оптимального управления, когда оно не ограничено, либо хорошее приближение к оптимуму в случае ограниченного управления для последующего итерационного улучшения в исходной задаче.