Уменьшение размера фокального пятна при радиальной поляризации с помощью бинарного кольцевого элемента

Узкая кольцевая апертура, блокирующая излучение практически во всей центральной части линзы [1 –3], является простым, хотя и энергетически затратным способом формирования узких протяжённых пучков в фокальной плоскости.

Более сложные способы полноапертурной аподизации функции зрачка как с помощью чисто фазовых, так и амплитудно-фазовых распределений рассмотрены в работах [4–9]. При этом, как правило, уменьшение размеров фокального пятна сопровождается перераспределением энергии из центральной части в боковые лепестки. Данная ситуация вполне согласуется с теорией Toraldo di Francia [10], в соответствии с которой можно получить сколь угодно узкое центральное пятно за счёт роста боковых лепестков, иногда в несколько раз [8, 9] или даже порядков [11] по сравнению с центральным световым пятном.

Наличие существенных боковых лепестков ограничивает применение «суперразрешающих» элементов в изображающих системах и при оптической записи данных, когда приемлемым считается уровень интенсивности в боковых лепестках менее 30 % по отношению к центральному пику [12].

Однако оптимизационные процедуры, позволяющие контролировать рост боковых лепестков, приводят к неизбежному уширению размера центрального пятна [12, 13].

В работе [13] было показано, что внесение радиального фазового скачка на π радиан по среднему радиусу узкой кольцевой апертуры приводит к уменьшению размера центрального пика до FWHM = 0,33 λ , что меньше, чем для простой кольцевой диафрагмы ( FWHM = 0,36 λ ). В этом случае уровень интенсивности боковых лепестков составляет менее 30% от главного пика и они могут быть отфильтрованы [14] или нивелированы при нелинейном взаимодействии света с носителями записи [15].

Уменьшение размера фокального пятна без существенного роста боковых лепестков достигается при введении радиального фазового скачка за счёт деструктивной интерференции двух пучков, формируемых каждым из колец в апертуре [15, 16]. Заметим, что обычно рассматривается полноапертурная аподизация зрачка объектива бинарными радиальными элементами [4, 6 –8, 16 – 19], однако в работе [20] было численно показано, что диафрагмирование центральной части линзы (около 75 % по радиусу) приводит к значительному улучшению результатов.

В данной работе аналитически и численно исследуется влияние размеров кольцевой диафрагмы с внесённым радиальным фазовым скачком на формируемое фокальное пятно в случае радиальной поляризации.

Анализ скалярной и векторной моделей острой фокусировки с использованием интегральных выражений Ричардса–Вулфа [21] выявил различие зависимости размеров фокального пятна от ширины узкой кольцевой диафрагмы. В первом случае предельный размер фокального пятна достигается при бесконечном сужении пропускающего периферийные лучи кольца, которое сопровождается квадратичным относительно ширины кольца падением амплитуды в фокусе. Во втором случае минимальный размер фокального пятна достигается при фиксированной ширине кольцевой диафрагмы. При этом амплитуда в фокусе пропорциональна ширине кольца в степени 3/4.

Численное моделирование показало, что, несмотря на деструктивную интерференцию, при достаточно широкой кольцевой апертуре можно существенно увеличить интенсивность в фокусе, не превышая предел, соответствующий узкой кольцевой апертуре.

1. Анализ уменьшения размера фокального пятна в скалярном случае

Фокусировка ограниченной плоской волны с помощью линзы радиусом R и фокусным расстоянием f описывается преобразованием Фурье–Бесселя, и интенсивность в фокальной плоскости имеет вид:

R k I kp r I

I (P) = "7 J ⁷ o | z I r ^d r f 0 I f J

R [ k p R ⁷ 1 1

P I f

что соответствует формированию в фокальной плоскости линзы картины Эйри.

Формально для получения в фокальной плоскости бесселевого пучка необходимо применить преобразование Фурье–Бесселя для бесконечно узкой кольцевой апертуры:

kR ² ₇ [ k p R | f I f J

Числовая апертура линзы с радиусом R и фокусным расстоянием f определяется из соотношения:

NA_lens = n sin θ = n sin

R arctg _f

которое в параксиальном случае сводится к выражению

nR

NA lens ^≈ f

.

Размер фокального пятна, формируемого в рас-

сматриваемых случаях, характеризуется следующи-

ми величинами.

Радиус центрального пятна при фокусировке с полной апертурой (1) определяется первым нулём функции Бесселя первого порядка ( J 1 ( γ 11 ) = 0, γ 11 = 3,83):

0,38

ρ ring ≈ NA λ .                                   (10)

Как видно из сравнения выражений (5) и (9), внесение кольцевой диафрагмы позволяет уменьшить размер фокального пятна в 1,6 раз.

При этом минимальная оценка для диаметра фокального пятна по уровню полуспада интенсивности:

FWHM m ^ri i ⁿ n ^g = 0,357 λ ,                        (11)

что в 1,44 раза меньше, чем для полноапертурного освещения, а для площади пятна по уровню полуспада интенсивности:

I                   ring 1

HMA ^ring =π⋅ FWHM ^min    = 0,1 λ ² ,         (12)

min               ₂

что соответственно меньше в 2,1 раза.

Заметим, однако, что в (2) не учитывается уменьшение амплитуды в связи с уменьшением освещаемой площади, т.к. значение δ -функции предполагается равным бесконечности.

Рассмотрим кольцо не бесконечно узкое, как в (2), а конечной ширины, составляющей малую долю ∆ от радиуса линзы. В этом случае амплитуда определяется выражением k R    I kr P1

E » ( P ) = 77^exP ^{( ikf} ) J ⁷ d ItI ^{r d r} .          ⁽¹³⁾

f          R (1-Л) I ^f J

С учётом малости ∆ приближённо возьмём интеграл (13), умножив значение подынтегральной функции в средней точке rs =R(1-∆/2)

ρ lens

3,83 λ f ₌ 061 λ f

2 π R    , R

на длину отрезка:

E _∆ ( ρ ) = ikf exp( ikf ) ×

В параксиальном случае

×

R ² ∆ ( 1 -∆ /2 ) J ₀

ρ lens

0,61

λ

NA

I k p R ( 1 -A /2 ) 1

I f J

Минимальная оценка для диаметра фокального пятна по уровню полуспада интенсивности (при NA =1):

kR ² ∆ if

exp( ikf ) J ₀

FWHM _m ^le _i ⁿ _n ^s = 0,515 λ

и для площади пятна по уровню полуспада интенсивности:

HMA m ^le i ⁿ n ^s =π⋅ ( FWHM m ^le i ⁿ n ^s /2 ) ² ≈ 0,21 λ ² .         (8)

При фокусировке с узкой кольцевой диафрагмой (2) радиус фокального пятна определяется первым нулём функции Бесселя нулевого порядка ( J 0 ( γ 01 ) = 0, γ 01 = 2,405):

Мы видим, что в таком приближении размер пятна такой же, как для бесконечно тонкого кольца, однако теперь учитывается уменьшение амплитуды в центре пропорционально уменьшению ширины кольцевой апертуры ∆ . Если в аргументе функции Бесселя не заменять R ( 1 -∆ /2 ) на R , то радиус пятна станет несколько больше.

Теперь рассмотрим уменьшение радиуса пятна путём введения фазового скачка на π радиан по центральному радиусу узкой кольцевой апертуры:

ρ ring

2,4 λ f 2 π R

= 0,38 ^{λ f} . R

τ ( r ) =

В параксиальном случае

, 1, ^r <  R [ 1 ^-A) exp( i n ), r >  R ^[ 1 — ^A

При этом получим распределение в фокусе, соответствующее деструктивной интерференции пучков, формируемых отдельными кольцами:

Et(P) = k           R 'krp)

= — exp(ikf) J T(r)J0 Нт I r dr = f           R (1-Д)        к f )

селя (18) значение корня оказывается на 20 % меньше истинного. Поэтому будем считать более правильным следующее значение:

X f

P ^Jump =1 ^n jump =Л 99^ min    ^x, "-rmin a ^u, r "

[ R ( 1-Д/2)    / А

= —exP ⁽ ikf )    J ^J 0 I "^Т I r d r

lf             R (1-Д)    к f )

^R ( 1- ^Д )

Эта оценка предсказывает уменьшение радиуса по сравнению с полноапертурной линзой в 2,8 раза, а по сравнению с узкой кольцевой апертурой – в 1,7 раза.

Минимальная оценка для диаметра и площади фокального пятна по уровню полуспада интенсивности:

.

R ( 1-Д/2 ) к f )

С учётом результата (14) можно записать:

_ , x Д kR ²

Eт(р) = у—exP(ikf)x

2 if

FWHM mmum’ = 0,26 X , HMA mmuim = 0,0532 X ² .

x

J ₀

kpR (1 - 3Д /4)

-

-

f

kpR (1-Д/4)

f

Чтобы оценить полученный в (17) результат для малых значений p , воспользуемся приближённым выражением для функции Бесселя через ряд Тейлора [22]:

Jv (x ^ 0) ~

x

1 -

x ²

1 f x Y ----- - x

r(v +1) ( 2 )

x ⁴

4(v +1) + 32(v + 1)(v + 2) ... .

Тогда вместо (17) приближённо получаем:

E■ (ph’

x

1 -

Д) kR ²

- I — exP(ikf)x

² ) if

Y L 15 A 13 Д2

3Д + Д

W 8   16

.

Отрицательное значение в нулевой точке означает изменение фазы на п по сравнению с падающим пучком. Первый коэффициент в правой части (19) показывает, что амплитуда в центральном пятне бу-

дет падать пропорционально квадрату ширины кольцевой апертуры. Радиус пятна находится из условия равенства нулю выражения в квадратной скобке и равен:

Р jump

X f

15    13

п R. 3 Д +— Д ² 8     16

.

Так как Д <  1, то наименьший радиус в (20) достигается при Д ^ 0 и равен:

Р=_ a =nf ‘ 0’184 ^f.               (21)

Заметим, что оценка (21) является заниженной, т.к. при квадратичной аппроксимации функции Бес-

Заметим, что в этом случае диаметр фокального пятна по уровню полуспада интенсивности (23) больше, чем радиус до нулевого значения (22). Эта ситуация отличается от той, что мы наблюдали для функций Бесселя первого и нулевого порядка (когда параметр FWHM был меньше радиуса до нуля), и говорит о большей крутизне боковых поверхностей центрального пика.

2. Анализ уменьшения размера фокального пятна при острой фокусировке радиально-поляризованного излучения

Известно, что при острой фокусировке радиально-поляризованного излучения и введении узкой кольцевой апертуры основной вклад в фокальную область вносит продольная электрическая компонента электромагнитного поля [1 –3]. Значительное превалирование одной компоненты над другими со-

ставляющими векторного поля приводит к ситуации, близкой к скалярному режиму. Это позволяет успешно использовать инструменты скалярной теории и достигать близких результатов (как правило, размер фокального пятна при острой фокусировке оказывается больше скалярной оценки из-за вклада в фокальную область различных компонент).

С учётом приведённых выше рассуждений рассмотрим только продольную компоненту при фокусировке радиально-поляризованного излучения. При наличии узкой кольцевой апертуры мы получим следующее выражение [9]:

E ; z ( p ) = J x ² ( 1 - x ² J '' J ₀ ( k p x ) dx =

1-Д

Д ( 1 -Д /2 ) 2

1/4

[1 -(1 -д/2) ]

J ₀ ( k р ( 1 -Д /2 ) ) .

Таким образом, размер фокального пятна, как и в скалярном случае (см. (14)), определяется первым нулём функции Бесселя нулевого порядка. Следова-

тельно, в пределе при уменьшении ширины кольцевой апертуры Д ^ 0 мы получим:

p m ™g = "NA X-^^ p- ng = 0,38 X .

Большего уменьшения размера фокального пятна без существенного роста боковых лепестков можно достичь на основе деструктивной интерференции, введя фазовый скачок на л радиан по центральному радиусу узкой кольцевой апертуры (15). Тогда распределение поля в фокальной плоскости описывается следующим выражением:

E Т ( р ) = J x ² ( 1 - x ² ) '' J 0 ( к р x ) d x - 1-Д

- J x ² ( 1 - x ² )    J 0 ( к р x ) d x .

1-Д/2

Для вычисления интегралов в (27) воспользуемся сначала способом, приведённым в разделе 1, тогда

Д (1 - 3 Д /4) 2       , ,                 Д (1 -Д /4) 2       , ,

E ( р )       ------- J о ( k р ( 1 - ^{3 Д /4} ) ) -— J о ( k Р ( 1 -^{Д 4}

2 | 1 - ( 1 - 3 Д /4 ) 2 I                          2 | 1 - ( 1 -Д /4 ) 2 I

Д ³/⁴ ( 1 - 3 Д /2 )

”       2

3 ( 1 - 3 Д /8 )

1/4

. I ¹

к ² р ² ( 1 - 3 Д /4 ) 2 '

Д ^3/4 ( 1 -Д /2 )

( 1 -Д /8 )

1/4

. I ¹

^{k 2} р ² ( 1 ^{-Д /4} ) ² '

.

Учитывая, что

( 1 ±0 ) ^- “ = 1 + а6+ ^а(( 2 ^- 1) 0 ² +

+ ... + ( + 1) n ^{а ( а- 1)...( а-} n ⁺ 1) 0 n + n !

+ ...,    10| <  1, а> 0,

выражение (28) преобразуется следующим образом:

3/4

E Т ( р ) ”

3 Д /2 )

3 1/4

X

h 3Д

X 1 +

I 32

к ² р ² ( 1 - 3 Д /4 ) ²'

V

При полной апертуре ( А^ 1) выражение (31) предсказывает меньший размер:

р zjump --— 0,75 П” 0,239 ^ .            (33)

Разумеется, оценка (33) является некорректной, т.к. формула (31) была получена в предположении малости Д , однако она указывает на возможность получения лучших результатов для относительно широких кольцевых апертур.

Рассмотрим более точное вычисление интегралов в (27). В частности, отметим, что эти интегралы несобственные, поэтому полученный в (30) результат требует коррекции.

Наиболее простой и приближённый способ коррек-

- ( 1 -Д /2 ) ⁽ 1 + —

V          ! V 32

(

^{1 -}

V

к ²р² ( 1 -Д /4 ) ² )

Далее, пренебрегая в квадратных скобках степе-

нями Д выше первой, получим:

E Т ( р ) ”

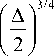
X

X J ( 0,24 + 0,6 Д ) - ^{к р} ( 0,24 + 1,24 Д ) .

Таким образом, в фокусе ( р = 0) будет ненулевая амплитуда. Радиус центрального светового пятна находится из равенства нулю выражения в фигурных скобках и оценивается следующей величиной:

ции в таких случаях сводится к умножению на поправочный коэффициент, аналогично тому, как было описано в работе [23]. В рассматриваемом случае коэффициент равен 4/(3 • 2 ^1/4 ) - 1,12, что приведёт лишь к небольшому увеличению амплитуды центрального пятна, но никак не скажется на оценке его размера.

Более кардинальный способ коррекции состоит в том, чтобы рассматривать не всё подынтегральное выражение в средней точке, а только функцию Бесселя. Тогда вместо (28) запишем:

E ; ( р ) - J 0 ^{( к} р ( 1 ^{- 3 Д /4 ))} _{( Т}-3Д_{77 )} ^X

_ % /0,24 + 0,6Д р” л^ 0,24 + 1,24Д .

Как следует из (31), при уменьшении ширины кольцевой диафрагмы:

р zjump .     .. 0,318 % ,                         (32)

что меньше, чем для кольца без скачка ( р    = 0,38 % ).

Однако из (31) также видно, что размер центрального пятна будет уменьшаться не с уменьшением ширины кольца, а наоборот, с её ростом, т.к. коэффициент при Д в знаменателе больше.

x _- 1 x ² (1 - x ²)’" -⁴⁴ (1 - x ² Г

- J₀(k р (1 -Д/4))----¹---- X

^0V            "( 1 -Д /4 )

2 2/, 2?/4 8/,    2V/4

^{X -} 3 x ^{( 1 -} x ) ^- 21 ^{( 1 -} x )

1-Д/2

1-Д

1-Д/2

Далее, сохраняя члены, содержащие Д вплоть до второй степени, получаем:

E z ( р ) ”-Д ^3/4 7 0,213 + 0,386 Д- 1,139 Д ² )-

7 2 2                                                     1

4- ( 0,213 + 0,734 Д- 2,175 Д ² ) .

Из выражения (35) получаем более точную, чем (31) оценку для радиуса фокального пятна:

λ

^Р z , jump п

0,213 + 0,386 A- 1,139 A ²

0,213 + 0,734 A- 2,175 A ² ’

который имеет минимум при A m = 0,168 .

Таким образом, минимальный радиус центрального светового пятна оценивается следующим значением:

Р zJump ( A m ) = 0,301 % ,                           (37)

что несколько меньше оценки (32).

3. Численные результаты

Оценки, приведённые в предыдущем разделе, являются приближёнными, но они позволяют анализировать зависимость размеров и интенсивности фокального пятна от ширины кольцевой апертуры. В данном разделе выполнено численное моделирование острой фокусировки радиально-поляризованного пучка с использованием интегральных выражений Ричардса-Вулфа [21].

На рис. 1 показана зависимость диаметра фокального пятна по уровню полуспада полной интенсивности ( FWHM) от ширины кольцевой диафрагмы ( A ) при отсутствии и наличии радиального фазового скачка (15). Точечная горизонтальная линия соответствует скалярному пределу для линзы ( FWHM=0,51 % ), а сплошная толстая - скалярному пределу для бесконечно узкого кольца ( FWHM =0,36 % ).

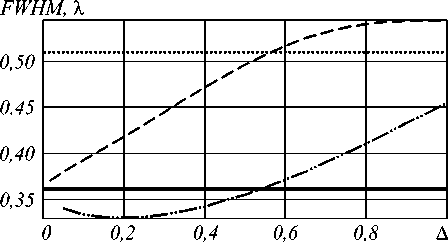
Рис. 1. Зависимость диаметра фокального пятна по уровню полуспада интенсивности (FWHM) от ширины кольцевой диафрагмы ( ∆ ) при отсутствии (пунктирная линия) и наличии (штрихпунктирная линия) радиального фазового скачка

Как видно из рис. 1, при использовании простой кольцевой диафрагмы для преодоления скалярного предела линзы (в общей интенсивности учтены все компоненты электрического поля) необходимо блокировать центральную часть линзы радиусом 0,43 R ( A = 0,57), что составляет около 20 % площади линзы. При этом результаты, соответствующие бесконечно узкой диафрагме ( FWHM =0,36 % ), не достигаются даже при очень малой ширине (при A = 0,01 FWHM =0,367 % ).

В случае наличия радиального фазового с качка (15) для преодоления скалярного предела линзы нет необходимости блокировать какую-либо часть линзы. Блокировка же центральных лучей на ра- диусе 0,46 R (A = 0,54, закрывается также около 20 % площади) позволяет получить фокальное пятно менее скалярного предела для бесконечно узкого кольца.

Заметим, что минимальный размер FWHM= 0,329 % достигается при ширине кольцевой апертуры A _m = 0,2 (рис. 1). Эта величина оказалась примерно в 1,2 раза больше размера, полученного в предыдущем разделе и использованного для оценки (37).

На рис. 2 показана зависимость приведённой интенсивности фокального пятна от ширины кольцевой диафрагмы ( A ) при отсутствии и наличии радиального фазового скачка. Вертикальные точечные линии соответствуют ширине кольцевой диафрагмы, при которой формируется фокальное пятно с FWHM = 0,38 % : для простой кольцевой диафрагмы

A =0,06, а при наличии фазового скачка A =0,65. Видно, что интенсивность в фокальном пятне в случае введения фазового скачка при более широкой коль-

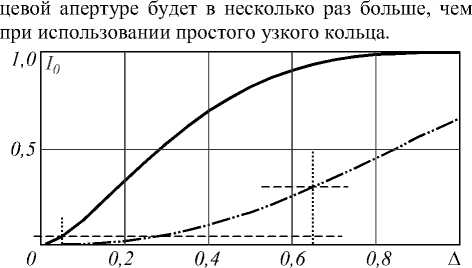
Рис. 2. Зависимость приведённой интенсивности фокального пятна от ширины кольцевой диафрагмы ( ∆ ) при отсутствии (сплошная толстая линия) и наличии (штрихпунктирная линия) радиального фазового скачка

В табл. 1 приведены результаты численного моделирования острой фокусировки ( R =100 % , у =101 % ) радиально-поляризованного пучка при наличии узкой кольцевой диафрагмы и фазового скачка (15): A - ширина кольцевой щели, 1 0 - значение общей интенсивности в фокусе, А - отношение общей интенсивности в первом боковом лепестке к общей интенсивности в центральном световом пятне, FWHM - диаметр центрального пятна по уровню полуспада в общей интенсивности, FWHM Z - диаметр центрального пятна по уровню полуспада в интенсивности продольной компоненты.

Как видно из приведённых в табл. 1 результатов, максимальное сужение центрального фокального пятна ( FWHM = 0,329 % , см. вторую строку в табл. 1) происходит без неприемлемого р оста боковых лепестков ( А < 0,3), но при существенной потере энергии в центральном пятне - интенсивность I ₀ в 2 раза меньше по сравнению с узкой кольцевой диафрагмой (первая строка табл. 1). По продольному распределению видно , что уменьшение пятна происходит за счёт деструктивной интерференции пучков, прошедших через различные кольца в апертур е.

Таблица 1. Результаты численного моделирования

Пропускающая функция

Продольное распределение интенсивности (негативное изображение), 3% x 6%

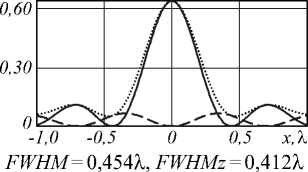
Поперечное распределение интенсивности в фокусе (негатив), 3 X x 3 X

Сечение для интенсивности компонент в фокусе (пунктирная линия – поперечные, сплошная линия – продольная, точечная линия – общая)

О 20 40 60 80 R ring, A = 0,05

I 0 = 0,044

S =0,162

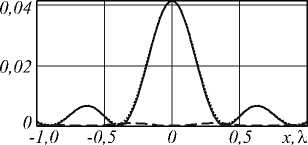
FWHM =0,378 % , FWHMz = 0,372 %

I 0 =0,02

S =0,279

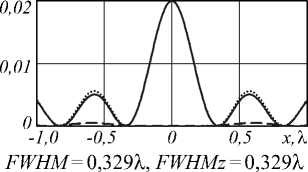
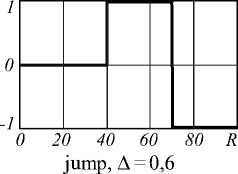
I 0 =0,25

S =0,351

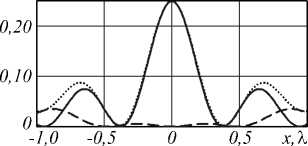
FWHM =0,371 % , FWHMz = 0,363 %

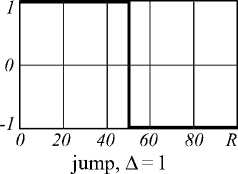
I 0 = 0,656

S =0,171

Однако за счёт увеличения ширины диафрагмы можно значительно повысить энергию в центральном пятне, не увеличивая размер пятна, который формируется узким кольцом. В частности, при A =0,6 (третья строка табл. 1) размер пятна немного меньше ( FWHM = 0,371 % ), а интенсивность почти в 6 раз выше по сравнению с узкой кольцевой диафрагмой. Недостатком является некоторый рост боковых лепестков ( S = 0,35).

Если рассматривать полную апертуру ( A = 1, четвёртая строка табл. 1), то наблюдается не только увеличение интенсивности в фокусе, но и спад боковых лепестков. При этом размер фокального пятна ( FWHM = 0,454 % ) не превышает скалярный предел, соответствующий картине Эйри.

Заключение

Анализ скалярной и векторной моделей острой фокусировки выявил различие зависимости размеров фокального пятна от ширины узкой кольцевой диафрагмы.

При описании фокусировки в скалярном случае преобразованием Фурье минимальный размер фо- кального пятна достигается при бесконечном сужении периферийной кольцевой апертуры, которое сопровождается квадратичным относительно ширины кольца падением амплитуды в фокусе.

В векторной модели острой фокусировки (в приближении Дебая) радиально-поляризованного пучка минимальный размер фокального пятна достигается при фиксированной ширине кольцевой диафрагмы, составляющей 20% от радиуса полной апертуры. При этом амплитуда в фокусе пропорциональна ширине кольца в степени 3/4.

Аналитически и численно показано, что за счёт деструктивной интерференции, создаваемой кольцами с различной фазой внутри кольцевой апертуры, можно преодолеть скалярный предел, соответствующий функции Бесселя нулевого порядка ( FWHM =0,36 % ). Уменьшение размера фокального пятна ( FWHM =0,33 % ) сопровождается уменьшением интенсивности в фокусе и небольшим ростом боковых лепестков, которые, однако, не превышают 30 % интенсивности центрального пика.

Численно показано, что внесение радиального фазового скачка на π радиан по среднему радиусу апертуры обеспечивает преодоление скалярного предела (картина Эйри, FWHM =0,51 λ ) даже для полноапертурной линзы. Блокировка же центральных лучей на радиусе 0,46 R (закрывается около 20% площади) позволяет получить фокальное пятно, размер которого менее скалярного предела, соответствующего функции Бесселя нулевого порядка. При этом интенсивность в фокусе почти в 6 раз больше, чем при использовании обычной узкой кольцевой апертуры, но наблюдается некоторый рост боковых лепестков, интенсивность которых составляет 35 % от центрального пика.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы» (Государственный контракт No 07.514.11.4055), а также грантов РФФИ 10-07-00109-а, 10-07-00438-а, гранта Президента РФ поддержки ведущих научных школ НШ-4128.2012.9.