Уменьшение вычислительных затрат при идентификации местоположения фрагментов на больших изображениях

В последние годы продолжается расширение области применения систем извлечения информации, использующих пространственные апертуры датчиков сигналов. Такие системы используют для дистанционного исследования Земли, в медицине, навигации, радиолокации, при обеспечении государственной безопасности и в других областях. Исходной информацией в них являются динамические изображения, при обработке которых одной из проблем является поиск по эталону, идентификация и определения параметров местоположения фрагментов изображений. При этом эталонный и искомый фрагменты могут иметь существенные взаимные геометрические и яркостные деформации.

Известные методы оценивания местоположения фрагмента основаны на четырех подходах:

• -    сопоставление изображения и фрагмента [1-2], при котором выделяют некоторое множество ярко выраженных признаков (точки или их группы, контуры, углы, перекрестья и т.п., при этом на исследуемых изображениях требуются наличие и стабильность выбранных признаков) и устанавливают соответствие между признаками;

• -    пространственно-временная фильтрация [3], при которой для поиска фрагмента параметры фильтрации подстраиваются по пространственным частотам (при этом используется информация, содержащаяся во всем фрагменте, поэтому

метод малочувствителен к локальным пространственным деформациям);

• -    морфологический анализ [4], использующий понятие формы объекта как инварианта заданного класса преобразований изображений;

• -    анализ оптического потока [5-6], при кото-ромисследуетсявекторноеполескоростейдвиже-ния точек яркостей сцены или их характеристик (например, таких как контрастность, градиент, энтропия и т.д.), причем яркость изображения, как правило, считается неизменной во времени.

К методам, использующим оптический поток, можно отнести и методы, основанные на оценке градиента целевой функции (ЦФ), среди которых для изображений больших размеров наиболее перспективной представляется идентификация и определение местоположения фрагмента на базе псевдоградиентных процедур [7]:

• a, = a_t__A -X₍PPQ),

где a – искомый вектор параметров местоположения фрагмента; X_t – матрица усиления; P_t – псевдоградиент ЦФ Q , характеризующий качество оценивания. При ограниченности вычислительных ресурсов и незначительных яркостных искажениях между опорным и искомым фрагментами в качестве ЦФ целесообразно выбирать средний квадрат разности яркостей искомого и опорного фрагментов, а при яркостных искажениях, близких к линейным, – коэффициент корреляции [8].

При нахождении псевдоградиента Pt (6) для повышения быстродействия процедур используют локальные выборки t 1 ^ jt a I небольшого объема, где z-^¹ – фрагмент Z^f , z_]t =zU,a_t_p – отсчеты непрерывного изображения Z , полученного из исследуемого изображения Z .

Постановка задачи

Псевдоградиентные процедуры рекуррентны, сочетают хорошие точностные характеристики с высоким быстродействием, применимы к обработке изображений с плавно меняющейся неоднородностью. Формируемые ими оценки параметров устойчивы к импульсным помехам и сходятся к оптимальным значениям при довольно слабых условиях [9].Однако в практических задачах из-за ограниченности вычислительных ресурсов требуемая точность оценивания параметров a достигается не на всем исследуемом изображении, а лишь в некоторой подобласти, ограниченной рабочим диапазоном процедуры [10].

Это приводит к необходимости разбиения изображения на N подобластей, соответствующих рабочему диапазону. Процедуру, работающую в подобласти, которой принадлежит искомый фрагмент, будем называть V-процедурой (от veritas – истинная). Процедуры, работающие в других подобластях, будем называть Р-процедурами (от pseudo – ложная). В результате работы все х процедур формируется N векторов a^J = \,N , оценок параметров местоположения фрагмента и возникает задача определения среди них с требуемой доверительной вероятностью подобласти, в которой достигается экстремум ЦФ.

Принцип управления множеством процедур

При решении задач поиска и идентификации фрагментов число подобластей может достигать нескольких тысяч [11]. Столько же будет и процедур. Если все процедуры выполнят одинаковое число итераций, обеспечивающее необходимую точность оценивания, то это потребует больших вычислительных затрат. Для сокращения объема вычислений может быть использован следующий принцип структурной оптимизации (управления множеством процедур) [12].

На каждом шаге алгоритма приоритет выполнения очередной итерации предоставляется процедуре, имеющей наименьшее значение некоторой функции штрафа ул . При этом под «шагом алгоритма» понимается совокупность операций, включающая: выполнение процедурой с минимальным штрафом очередной итерации, нахождение нового значения штрафа и определение процедуры с наименьшим штрафом.

Сложность состоит в том, что при этом требуется сравнение штрафов процедур, выполнивших разное число итераций. Исследование требований к ул , обеспечивающих такую возможность, показало, что при использовании ЦФ, подлежащей минимизации, такому условию удовлетворяет функция

• V^ = ^4^^ ,

7=1

где Qmin ^ inf { Q j } – величина, меньшая нижней г ран ицы множества t'/’,;^!,^ оценок ЦФ; i-\,N . Если же ЦФ подлежит максимизации, то

dr^Q^-pl,

7=1

где 5max ^SUp{9y,}.

Плотность распределения вероятности функции штрафа

Функция штрафа ул зависит от способа формирования локальной выборки Z _t . Причем в процессе сходимости оценок параметров местоположения фрагмента к оптимальным значениям вероятностные свойства ул изменяются. Поэтому для анализа и оптимизации ул желательно знать ее плотность распределения вероятностей (ПРВ) w,(^) на каждой итерации. При этом в качестве меры соответствия отсчетов I Z'- } £ Z и ! ^7/}^ ^ ' входящих в локальную выборку, целесообразно использовать коэффициент корреляции ρ, который является одномерной характеристикой, не зависящей от способа интерполяции изображения Z и числа оцениваемых параметров. Тогда ПРВ приращения Δ ψ , штрафа на каждой t -ой итерации:

Wt (А ул) = Jw, (А ул/pXp^dp, где w,W/p) – условная ПРВ приращения; w(ρ) – ПРВ коэффициента корреляции. Заметим, что для Р-процедур ПРВ w,Wlp = ^ не зависит от номера итерации. Тогда ПРВ на t-ой итерации w, (y/) = Jw,_, (у/ - А ул, )w(A tp^dN ip .

Для V-процедур по мере сходимости вектора оценок ex к истинным значениям ρ увеличивается, поэтому w,W/p) зависит от номера итерации. Соответственно,

^WI ^ ⁼ J J^w'-1 ^ -^V>, (Аул/ pMP^dApdp •

С использованием приведенных соотношений несложно получить выражения для расчета ПРВ ψ для таких часто используемых ЦФ, как средний квадрат разности и коэффициент корреляции [10].

Вероятность ошибочного выбора фрагмента

Если априорно неизвестно наличие искомого фрагмента на исследуемом изображении, то возникает задача проверки гипотезы, что среди. N исследуемых подобластей нет подобласти, содержащей фрагмент. Для ее решения предлагается использовать статистический критерий: если за М = М_kr шагов алгоритма ни одна из N процедур не достигла Т_м -ой итерации, то среди исследуемых подобластей подобласть фрагмента отсутствует. Выбор величин Т_м и М_kr позволяет обеспечить нужные вероятности ошибок первого (P ⁽¹⁾ ) и второго (Р ⁽²⁾ ) рода. Вероятности Р ⁽¹⁾ и P ⁽²⁾ можно найти по дискретным распределениям P_Vt и Р_Рt , числа итераций для V- и Р-про-цедур, где Р_V(Р)t – вероятность того, что за М_kr шагов алгоритма V(Р)-процедура выполнила t итераций при разбиении иссле дуем ого изображения на N подобластей; ^ — h Т_м . Несложно показать, что

^PdOr ~ /^ГЛ/О^ЗО ^Pd'i/C^))^^   ^^Pd'); ’

О                                              '=1

где ^ДраЛЧ^) — J^jj/^Cx)^ – функция распре-

О деления ψ на t-ой итерации Р(V)-процедуры;

^WTM ^ ) ^— W₍T_A/ (^ )(1 Fр_ТМ (у/ ))   +

+ ™V™4v^-FVTMW) -

– ПРВ штрафа на Т_м -ой итерации, <"м^ – ПРВ минимального из ( N – l)-гo значений штрафов Р-процедур на Т_м и M_kr итерации. Тогда для заданных Т_м и M_kr

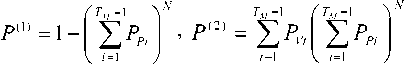
Другой важной характеристикой является вероятность P_er ошибочного выбора фрагмента. При наличии на изображении искомого фрагмента и предположении о независимости штрафов Р-процедур для верхней границы P_er получаем

P„w = jw_IT Vv )(1 - (1 - F_PT ^ ))^л'"' ^dy •

Для примера был проведен расчет вероятности пропуска фрагмента для случая, когда пара- метрами его местоположения являлись координаты центра фрагмента и угол поворота между эталонным и найденным фрагментами. Для 400 итерации оценивания при начальных рассогласованиях положения центра фрагмента в 5 шагов сетки отсчетов и угла поворота в 10 град. при N = 2 вероятность Реr\V составила менее 3·10-3, при N= 50 - PerW < 2 • 10"2, при N= 1 000 - PerW < 10"1.

Вычислительные затраты

Для анализа вычислительных затрат структурно оптимизированных процедур поиска найдены ди ск ретные распределения вероятностей ^рД, t-VT, числа итераций, выполненных процедурами для ситуаций наличия

Р, = Jwr(^)(l - Fp.^dy - Рр, и отсутствия

Pt="\<4VYX-FPlW-^LPp, О                                                          i на изображении искомого фрагмента, где W, (у/) – ПРВ штрафа на Т -ой итерации.

Использование структурной оптимизации позволяет существенно сократить вычислительные затраты. При этом выигрыш в быстродействии растет с увеличением размеров исследуемого изображения. Так, для изображений с гауссовской корреляционной функцией при 1000 итерациях оценивания выигрыш по сравнению со случаем, когда все процедуры достигают порогового числа итераций, составляет: при N = 50 – 1,6 раза; N = 200 – 2,5 раза; при N = 1000 – 5,3 раза.

Заключение

Разработанные алгоритмы поиска по эталону, идентификации и определения параметров местоположения фрагментов изображений могут найти применение при решении различных задач автоматизированной обработки изображений: обнаружения аномалий на последовательности космических снимков, «склейки» аэрофотоснимков, идентификации дактилоскопических отпечатков и радужной оболочки, отслеживании траектории подвижных объектов, идентификации лиц, номеров автотранспорта, при решении задач государственной безопасности и других. Несомненным достоинством предложенных алгоритмов является возможность вероятностного анализа достоверности получаемых результатов.