Унифицированное представление данных для генетических алгоритмов

Эффективность работы элементов биологических систем вызывает пристальный интерес к использованиюпринциповбиологическойэволю-ции для задач оптимизации систем, практически важных для самых различных областей [1].

По сравнению с обычными оптимизационными методами методы эволюционно-генетических вычислений (ЭГВ) имеют следующие особенности: параллельный поиск, случайные мутации и рекомбинации уже найденных хороших решений. Они хорошо подходят как простой эвристический метод оптимизации многомерных, плохо определенных функций.

Наибольшее распространение из ЭГВ получили генетические алгоритмы (ГА) [2]. ГА – это компьютерная модель эволюции популяции искусственных «особей». Каждая особь характеризуется своей хромосомой Sk, хромосома ин- терпретируется как «геном» особи и определяет приспособленность особи f(Sk); k = 1 ... n; n – численность популяции. Хромосома есть цепочка символов Sk = (Sk1, Sk2 ... SkN), N – длина цепочки. Символы интерпретируются как «гены» особи, расположенные в хромосоме Sk. Задача алгоритма состоит в максимизации функции f(Sk).

Эволюция состоит из последовательности поколений. Для каждого поколения отбираются особи с большими значениями приспособленности. Хромосомы отобранных особей рекомбинируются и подвергаются мутации. Формально, схема ГА может быть представлена следующим образом (популяция t -го поколения обозначается как { S_k ( t )}):

А0. Создать случайную начальную популяцию { S_k (0)}.

А1. Вычислить приспособленность f ( S_k ) каждой особи S_k популяции { S_k ( t )}.

А2. Производя отбор особей S_k в соответствии с их приспособленностями f ( S_k ) и применяя генетические операторы к отобранным особям, сформировать популяцию следующего поколения { S_k ( t + 1)}.

А3. Повторить шаги А1, А2 для t = 0; 1; 2 ... до тех пор, пока не выполнится условие окончания эволюционного поиска.

Имеется ряд конкретных вариантов ГА, которые отличаются по схемам отбора, рекомбинаций, по форме представления хромосом и т.д. Как метод оптимизации, ГА обладает внутренним параллелизмом: разные частные существенные комбинации генов отыскиваются параллельным образом, одновременно для всех комбинаций.

Каким образом случайный обмен и изменение подстрок совместно со смещенным, но все равно случайным методом селекции строк, полученных этими операциями, может обеспечить эффективный поиск? Дело в том, что следует рассматривать не строки в целом, а способ сохранения внутри строк отображений аллелей. Отображения аллелей называются шаблонами (в ряде источников [1] – шимами), они – просто строки, но с дополнительным отличительным признаком «#», который разрешен в каждой позиции. Это – групповой символ, означающий «не имеет значения», например, шаблонами для задачи представления <3,2,2> являются # # #, # # 0, # 1 #, 2 # #, # 0 0 , 0 # 1 и 2 1 0.

Шаблоны определены двумя величинами. Порядок шаблона – число определенных в нем аллелей (то есть, сколько символов отлично от #). Разрешение (длина разрешения) – расстояние между первой и последней определенной аллелью. Данные величины применяются для определения того, как шаблон поведет себя при рекомбинации: порядок определяет, насколько вероятно шаблон будет разрушен при мутации: большее количество аллелей означает большую вероятность мутации одной из них; разрешение определяет, с какой вероятностью шаблон может быть разрушен кроссовером: чем ни больше размер шаблона, тем больше вероятность того, что кроссовер произойдет в шаблоне. Случай кроссовера усложняется тем, что разрушение шаблона зависит от свойств взаимодействующих строк, например, если шаблон присутствует в обеих строках, кроссовер не может его разрушить.

При обработке шаблонов, если шаблон будет иметь тенденцию образовываться в строках с характеристиками выше средних, то вследствие более частого отбора этих строк и шаблоны будут отбираться чаще. Строки сами по себе часто разрушаются рекомбинацией, но с шаблонами, особенно короткими или низкого порядка, такое происходит существенно реже. Так, если шаблон возникает в «хороших» строках популяции, ГА произведет новую популяцию с большим количеством строк, содержащих такой шаблон, что и требуется. Если шаблон будет появляться на «хороших» строках и данное обстоятельство будет закреплено в популяции, то весьма вероятно, что полученные свойства будут объединены с другими интересующими нас свойствами, определяемыми другими шаблонами, что позволит сформировать строки с очень высокими значениями функции пригодности.

Такие аргументы могут быть ослаблены высоким уровнем взаимодействия между строками. Пусть шаблон H имеет тенденцию появляться на строках с неудачным набором свойств. Эти строки отбираются реже и присутствие шаблона в популяции падает, пока не исчезает совсем. Это плохо, поскольку комбинация H с шаблоном H' является частью оптимальной строки. Высокая степень взаимодействия между этими двумя шаблонами, таким образом, ведет к заключению для управляющей части ГА, что шаблон H не является ценным. Такое менее вероятно при коротком шаблоне или шаблоне низкого порядка. Хорошая комбинация H и H' может возникнуть при инициализации популяции или вследствие рекомбинации прежде, чем эти части строк будут потеряны. Если шаблоны будут более длинными или будут иметь более высокий порядок, то они с меньшей вероятностью появятся вместе при инициализации или вследствие рекомбинации, а с большей вероятностью будут разбиты рекомбинацией. Таким образом, если комбинирование действительно происходит, то его вероятность фактически управляет поведением популяции, поскольку последнее определяется соотношением селекции, усиливающей шаблоны, и рекомбинацией, их ослабляющими.

Неявный параллелизм, ключевые шаблоны и унифицированные преобразования

При обработке строк происходит также неявная обработка шаблонов. Смысл термина обработка в том, что шаблоны с характеристиками выше средних в следующем поколении будут встречаться чаще, с характеристиками ниже средних – реже. Игнорируя шаблоны, которые, вероятно, будут разрушены при рекомбинации, для каждых n обработанных строк (популяций размера n ) число обработанных шаблонов по оценке составляет О ( n ³ ) [5].

Рассмотрим, как обработка множества ключевых шаблонов может привести к свободной обработке всех других шаблонов. В качестве примера возьмем простейшую проблему представления <2>. Если известны средние оценки пригодности популяции, наблюдаемая пригодность шаблона 1 и удельный вес шаблона 1 в популяции, тогда мы можем вычислить ожидаемый удельный вес шаблона 1 в следующем поколении. Это вычисление – основа обработки шаблона, которую ГА делает неявно. Поскольку популяция содержит только 0 и 1, пропорции 1 определяет пропорции 0. Существенным является то, что обработка шаблона 1 – также обработка шаблона 0. Мы не можем обработать один, не имея в качестве побочного эффекта обработки другого. В примере имелся один ключевой шаблон, который мог быть либо 0, либо 1. Если количество элементов гена увеличить до c, то ключевых шаблонов станет c – 1; единственный оставшийся шаблон будет обработан неявно.

Рассмотрим представление <2,2>. Для однобитового аргумента при обработке 1# и #1 шаблоны 0# и #0 обрабатывались как побочные эффекты. Однако ни один из двухбитовых шаблонов не будет обработан как побочный эффект. Например, если мы знаем, что есть точно одно появление каждого из однобитовых шаблонов, мы не можем знать, содержатся ли в популяции 00,11 или 01,10. Если же мы обрабатываем также 11, тогда все остальные двухбитовые шаблоны обрабатываются неявно. Причина проста: если мы знаем, сколько имеется значений 11, тогда значения 1# , не связанные с 11, могут появиться только в 10. Точно так же оставшееся значение #1 может появиться только в 01, и остальная часть популяции должна быть представлена значениями 00. Для этого представления ключевыми шаблонами являются 1#, #1 и 11.

Может быть доказано, что, если есть n_S – 1 строк, то для того, чтобы все оставшиеся были обработаны как побочный эффект, должны быть обработаны n_S – 1 ключевых шаблонов (при рассмотрении удельного веса строк в совокупности используется n_S – 1 ключевой шаблон, поскольку шаблон ###...# всегда имеет удельный вес 1 и для упрощения игнорируется). Если мы рассматрива-емобработкувтерминахизменениянаблюдаемых оценок пригодности, тогда шаблон ###...# будет с наибольшей вероятностью обработан (потому что его оценка – средняя оценка всей популяции, и мы должны использовать n _S ключевых шаблонов). Эта форма более общая и применяется как основа унифицированного преобразования.

Применение ключевых шаблонов означает, что мы получили поддающееся трактовке представление об обработке шаблонов, поскольку можно ограничиться рассмотрением ключевых шаблонов; остальные ситуации обрабатываются автоматически как побочный эффект, поэтому необходим метод, позволяющий обеспечить рас- смотрение разных аспектов ГА (оценка пригодности, удельный вес в популяции и т.д.) с точки зрения различных ключевых шаблонов.

Двоичное и недвоичное представление

Двоичное кодирование или представление задачи для ГА традиционно означает, что решение задачи представляется в виде двоичных строк фиксированной длины. Недвоичное кодирование предполагает представление задачи строками фиксированной длины, содержащих аллели из дискретных генов, из которых все или часть не являются двоичными. Таким образом двоичное представление не является подмножеством недвоичного.

Термин «недвоичное кодирование» не является точным и применяется для того, чтобы подчеркнуть отличие данного представления от представления двоичных генов. Для точной характеристики вводится термин «обобщенное», или «унифицированное представление», оно применяется для описания генов, являющихся конечными множествами величин строк фиксированной длины и задач, основанных на представлении таких генов.

В пользу двоичного кодирования существуют два основных довода: 1 – количество шаблонов и 2 – охват аллели. Анализ показывает, что эти обстоятельства не обеспечивают безусловного преимущества во всех случаях.

Двоичное представление использует больше шаблонов, чем эквивалентное недвоичное. Например, для представления <4> используется 5 шаблонов (0; 1; 2; 3; #), в то время как представление <2,2> с тем же самым числом строк использует 9 шаблонов (00; 01; 10; 11; 0#; 1#; #0; #1; ##). Поскольку ГА обрабатывает шаблоны, то чем больше шаблонов, тем больше информации имеет ГА и тем лучше он будет функционировать.

Под ожидаемым охватом аллели понимается оценка удельного веса всех возможных аллелей в случайной популяции [1]. В основе лежит предположение, что чем ни выше значение характеристики гена, тем меньше можно ожидать, что все аллели гена будут воспроизведены в случайной популяции. Для двоичного кодирования строки разумно предположить, что все полезные аллели присутствуют в случайной начальной популяции, и высокий ожидаемый охват не обеспечивает нужного уровня обобщения для кодирующих структур повышенной сложности. Аналогичные результаты в работе [4] утверждают, что для мелких популяций вполне удовлетворительны двоичные строки, но в общих случаях популяции должны быть достаточно большими и аллели при этом должны быть определены не двоичным, а q-арным алфавитом.

Итак, двоичное кодирование дает больше шаблонов, чем недвоичное, однако поскольку эти шаблоны могут содержать информацию, препятствующую эффективной работе ГА, особых преимуществ это не дает. Недвоичное представление дает меньше шаблонов, но более высокого порядка.

Наконец, недвоичное представление аллелей может оказаться полезным при возрастании числа мутаций. Четверичная аллель действует как закрепленный двухбитовый шаблон за исключением того, что он занимает один локус вместо двух, а это означает, что шаблон будет меньше подвергаться мутации. Такой механизм компенсации возрастающего уровня мутации улучшает работоспособность ГА для недвоичного кодирования.

Альтернативная интерпретация шаблонов подразумевает, что лучшим кодированием задачи в целом является единственный ген, размер которого соответствует пространству поиска. Подобное кодирование превращает ГА в разновидность реализации алгоритма случайного поиска, управляемого мутацией.

Альтернативная интерпретация шаблонов является основным аргументом для применения недвоичного представления. С этой точки зрения символ # означает не «без различия», а «0 или 1». Такой подход ничего не меняет для двоичного представления, но для недвоичного вносит радикальные изменения. В качестве примера рассмотрим триарный ген {0; 1; 2}. Вместо единственного символа «без разницы» теперь для различных подмножеств будет задано множество «мелкомодульных» символов безразличия: #01 – позиция, где в строке могут появиться 0 или 1; #02 – соответственно 0 или 2, аналогично #12 и, наконец, вместо традиционного # используется #012. Для строк длины t и всех генов порядка c* при традиционной интерпретации имеем ( c * + l) t шаблонов, альтернативная интерпретация дает (2 c * – l) t и простой анализ показывает, что недвоичная кодировка дает для одинакового числа строк намного больше шаблонов.

Завершая сравнительное рассмотрение двоичного и недвоичного представлений, можно придти к выводу, что нет явных причин предпочесть один способ кодирования другому. Поэтому для обеспечения единой основы представления можно предложить введение единого унифицирован-

ного способа кодирования задачи для реализации ее средствами ГА.

Базовые понятия теории унифицированного представления

Введем основные понятия теории унифицированного (обобщенного) представления ГА. Они включают произведение Кронекера – базовую матричную операцию, обеспечивающую связь между структурой матриц, представляющих интерес для кодирования, и строками унифицированного представления; r -матрицы – матрицы, которые могут быть индексированы не числами, а строками, и k -матрицы, структура которых тесно связана с унифицированным представлением.

Произведение Кронекера (прямое или тензорное произведение, ПК) применяется для построения матрицы из двух меньшего размера путем использования правой матрицы в качестве «строительного блока» и масштабирования ее элементами левой матрицы

A⊗B=

A 11 B

A 2,1 B

A 1,2 B

^A 2 2 ^B

A ↓B

¹ n A

A ↓B

2 n _A

A

n

2 ^B

A → B n A ²

A _→↓ n _A n _A

B

где A - матрица n ^ x n A , B - матрица n ^ x n B , A ® B = n ^ n" ^ x n A n B . Из определения произведения Кронекера следует, что применив индексирование от 0, а не от 1, имеем:

(A®B) ^ ,.t , = AHB. , .

in _B ^→ +i ,in _B + j        ^{i , j} i ,J

Представлением задачи или просто представлением назовем вектор c целых чисел, такой, что ∀ _i c _i ≥ 2 . Размер представления задачи – произведение его элементов ∏ = 1.

Элементы представления задачи – характеристики генов. Они определяют число допустимых символов в каждом локусе строки, то есть характеристику гена в этом локусе. Далее считаем множество G i = {0;1;2... c i - 1} геном для локуса i и таким образом представление задачи становится эквивалентно набору строк.

ПК можно применить для формирования строк и представлений, используя операцию конкатенации <> :

Для любых представлений c , c ′:

П(с <> c') = ПсПС.

При дальнейшем рассмотрении желательно иметь возможность индексировать матрицы не числами, а строками. Для этой цели с матрицей должно быть связано представление задачи, которое точно определяет, какие строки могут быть использованы в качестве индекса матрицы. Такая пара «матрица – представление» называется r -матрицей.

Определение 1. r -матрицей назовем двойку <  M, c >, где M – матрица размером n × n и представление задачи c размера n , называемое основным или базовым представлением.

Определение 2. r -вектор – это двойка < ν, c >, включающая вектор v, вида n х 1 или 1 х n , и базовое представление задачи с размера n .

Для определения способа индексации строк или столбцов r -матрицы ( r -вектора) с помощью отдельных строк применяется функция отображения строк в числа

Значение r -матрицы ( M, c ), индексированной строками s и t , определяется как

^{( М} , С ) s t = M idx ( s , c ), idx ( t , c ) ■

Определим idx ( ). Для преобразования строки в число упорядочим все строки и положение строки в упорядоченной последовательности даст уникальное значение. Самым очевидным способом упорядочения строк является их упорядочение по числовому значению аллелей, начиная с крайних правых локусов по возрастанию значений. Например, строки двух триадных генов G = {0; 1; 2} упорядочиваются как 00; 01; 02; 10; 11; 12; 20; 21; 22.

Определение 3.

idx^^ = 0, idx(s* :: s, c* :: c) = s*Пс + idx(s, c).

Это определение дает возможность проводить декомпозицию векторов. Нам потребуется разделять вектора в выбранных точках и следующая теорема, приводимая без доказательства, обеспечит такие действия.

Теорема 1.

idx(s <>  s' , c <>  c' ) = idx(s, c ) nc' + idx(s c' ) .

К r-матрицам точно так же, как и к обычным матрицам, могут быть применены матричные операторы. Единственным отличием является необходимость рассмотрения базового представления. Для большинства операций базовые представления операндов и результат идентичны. Это приводит к следующему определению, расширя- ющему матричные операции O до применения к r-матрицам:

Определение 4. Если O – матричная операция, которая для операндов размера n х n , 1 х n , или n х 1 возвращает матрицы размера n х n , 1 х n , n х 1, то такая операция определена для r -матриц / r -векторов как:

O (( M i , C ),( M 2 , C ),...,( M m , С )) =

= ( O ( M 1 , M 2 ,..M m ), c ) ■

Данное определение дает r -матричный эквивалент операций для умножения матрицы на матрицу, матрицы на вектор, матрицы на число, транспонирование, инверсии, извлечение строк/ колонок.

Данное определение не распространяется на ПК, поскольку последнее изменяет базовое представление.

Определение 5. ПК для r -матрицы определим как ( M , c ) ® ( M ', c' ) = ( M ® M’,c <>  c' ).

Можно увидеть, что результат всегда будет r-матрицей, поскольку по определению ПК, M ® M' дадут матрицу ПсПСхПсПС и, размер c <>  С равен ПсПС .

ПК и функция idx ( ) дают интересные зависимости, как это показано в теореме 2.

Теорема 2. Если R и R′ являются r -матрицами, то ( R ® R' )s<>s-,tot- = RstRs^t -, где строки должны быть элементами базовых представлений r -матриц, которые они индексируют.

Доказательство. Пусть n – размер R ′.

(R ® R'\_s<>s'd<>l' ⁼ (^ ® ^')/A'(A<>5'),/*(/<>/') (определение           idx^)               =

= (^ ® R')n idxks^idx_W,n idxWidxvn (теорема 1) ^— Ridx^s^Jdx^R idx^s'\idxVt'^ ^s,?^ s’t' (определение idx()\

Большинство матриц в данной работе индексируются строками и также являются построенными с помощью ПК. Два этих подхода объединяются в концепции k -матриц.

Определение 6. k -матрица, K – это r -матрица с базовым представлением Cc 1 ; c ₂ ... cl) , где K = ® l = 1 K и каждое KK , называемое матрицей-ядром, является r -матрицей с базовым представлением c_i

В большинстве случаев с k-матрицами можно работать, не прибегая к idx(). Элемент k-матрицы может быть вычислен из определенных элементов ее матриц-ядер. Индексирование матриц-ядер так же эффективно, как и обычных матриц, поскольку из определения idx() и индексации (M, 0), = Ms,t.

Теорема 3. Если К является k-матрицей, s и t – строки из ее базовых представлений, то ci

K s,t = ∏ K S i ,t i .

i

Доказательство. Последовательно применить теорему 2 к определению K , данному выше.

Теорема 4. Если O является оператором r -матрицы, таким, что O (® i R i ) = ® . O . ( R . ) , r -матрицы транспарентны каждому O _i и K есть k. . -матрица, то O ( K ) является k -матрицей.

Доказательство.     O (K) = O (®(M i , (c i )))

^{= 0} OW’c^c^ (свойство O ) = ® ( O i ( M i ),(c i) ) (транспарентность). Последняя стр ⁱ ока повторяет определение Κ -матрицы, следовательно, теорема доказана.

Следствием этой теоремы является,что если K и K′ – матрицы с однотипным базовым представлением, то K – 1, KT , и K•K′ также будут k -матрицами.

Ниже рассмотрим два преобразования – преобразование объединения – инкрементной комбинации (ICT) и преобразование обобщенного разбиения – MPT. Они являются методами изменения «перспективы» рассмотрения изменением рассматриваемых множеств ключевых шаблонов. В общем случае для изменения перспективы требуется на что-то смотреть, что-то рассматривать, например, мы можем рассматривать оценку пригодности или пропорции изменения популяции, либо же некоторую комбинацию этих двух элементов. Для абстрагирования от таких деталей мы можем предположить, что имеется некоторая величина, связанная с каждой строкой, которую мы будем называть значением строки.С точки зрения шаблонов нас будет интересовать значение шаблона, которое является величиной значения строк в строках шаблонов.

Одним способом изменить перспективу рассмотрения является переход от значений строк к значениям шаблонов ключевого шаблона. Это можно осуществить следующим образом: матрица,пре-образующая значения строк в значения ключевых шаблонов, не содержащих нулей, являются k -матрицами с матрицами-ядрами следующего вида:

1/ c *

^K  =

1/ c *    ...   1/ c *

1      ...     0

0       0     ...     1

Однако вместо рассмотрения абсолютных значений шаблонов можно рассматривать отно- сительные комбинации. Шаблон #12# является комбинацией шаблонов #1## и ##2#. Первым приближением было бы вычислить значение шаблона #12# как z(#1##)+z(##2#). Естественно, между этими двумя одноаллельными шаблонами могут наблюдаться взаимные воздействия. Относительное значение шаблона #12# – это дополнительная величина, которую нужно добавить к указанному первому приближению, чтобы получить действительное значение шаблона #12#, таким образом использование относительных величин уменьшает уровень взаимодействия между двумя одноаллельными шаблонами.

Значения одноаллельных шаблонов берутся относительно значения ####, так действительное значение шаблона #12# будет e #### + e #i## + e ##2# + e #i2# , где e s — относительное значение шаблона, которое можно назвать коэффициентом разбиения.

Обобщение двоичных коэффициентов. Коэффициенты разбиения дают возможность вычислить значения строки или шаблона по вкладу их аллелей и являются формой относительного значения шаблона для отдельных множеств ключевых шаблонов. Для коэффициентов разбиения множество ключевых шаблонов – все шаблоны, не содержащие нулей.

Коэффициенты удобно рассматривать как «вклад» отдельных аллелей (или как преимущество от обладания отдельными аллелями).

Например, z_n = e ## + e i# + e #i + e_n, где e ## -среднее значение всех строк, e i# - дополнительное значение, которое в среднем строка дает при наличии 1 в первой аллели, e #i - соответственно, во второй. Любой или любые из этих коэффициентов могут быть отрицательными и в этом случае наличие 1 в соответствующей позиции уменьшает значение строки. e ii - дополнительное значение, которое дает комбинация единиц помимо индивидуальных вкладов отдельных единиц. При таком подходе значение целого не будет совпадать со значением составляющих его частей.

В двоичном случае налицо симметрия. Если строка не содержит в локусе 1, она должна содержать 0, то есть вклад, который строка будет иметь от наличия 0, к примеру, в первом локусе, равен потерям от отсутствия там 1, то есть e i# и z(10#) = e ### + e i## - e #i# - e ii# .

В недвоичном случае такая симметрия нарушается. Мы должны явно указать, какую аллель следует использовать или подразумевать при отсутствии других. Мы можем предположить, что подразумеваемой аллелью является 0, поскольку такой выбор объединяет выбор ключевых шаблонов (так как такой шаблон не содержит нулей). Используя такие значения для коэффициентов мы можем записать уравнения, связывающие коэффициенты разбиения и значения строк для задачи, представленной геном с характеристикой 4:

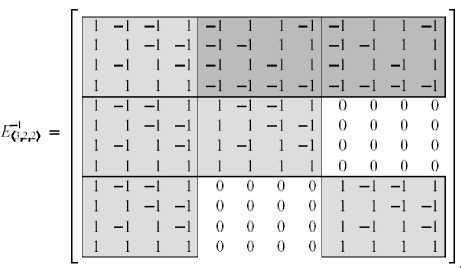
zo= e#       — ei — 62 — 63;

z1= e#+ e z2= e#+ e z3= e#+ e

где e -3 – вклады 1-3, а вклад 0 является вкладом ситуации отсутствия 1-3.

Обозначим матрицу обратного преобразования как E ^-1 и, следуя подходу, изложенному ранее для r -матриц, свяжем ее с базовым представлением задачи. В качестве примера возьмем уравнения:

Для отображения структуры использовано выделение фоном. На «верхнем уровне матрица состоит из 3 типов одинаковых блоков: все нули, блок со светло-серым фоном и блок с темно-серым фоном. Последний является полностью аналогичным блоку со светло-серым фоном, но у всех элементов изменен знак. Можно записать:

B

B

z0

z1

z2

z3

z < 4 >

⎡1

⎢⎢1

⎢1

⎣1

=E

E

' <3,2,2>

B

B

-

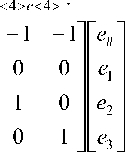
B0

B

что с точкизренияструктуры очень близкок Е < 1 >

Аналогично проанализируем структуру блока В:

Каждая строка матрицы преобразования соответствует вычислению значения строки базового преобразования:

Любая матрица E,C, >  для одного генома будет представлять матрицу размером с * х с * с 1 в первой столбце (поскольку каждое вычисление требует коэффициента «среднего значения»), 1 вдоль главной диагонали (для единственного коэффициента она должна быть добавлена к … и –1 в верхнем ряду со второй позиции (вычитая коэффициенты для подразумеваемой аллели). Аналогично

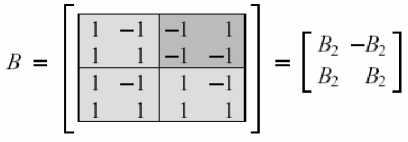
что, с точки зрения структуры, подобно Ej > .

Иными словами, крайний левый ген (характеристика 3) управляет глобальной структурой матрицы, используя Е < 1 > как шаблон, в котором размещены структуры низкого уровня. Второй

ген управляет промежуточными структурами, используя как шаблон Е <\> , и крайний правый

ген управляет локальной структурой, используя

E

'<2> •

ПК строит матрицы точно так же. Используя

его, можно записать:

E

-1

< c * >

-

I

c _* -1

где I_n – единичная матрица n×n .

От рассмотрения ситуации с одним геном перейдем далее. Начнем с рассмотрения E < 1 2 ₂ > и, анализируя ее структуру, выведем общую формулу для E;_c > .

- I           77-1       77-1       77-1

E<3,2,2> = E<3> ^ E<2> ^ E<2> или в общем случае

e <<1, m, n > = e < ® e ;m > ® e ;П > •

Сравнивая это равенство с определением k -матрицы, легко увидеть, что E ^-1 является k -матрицей.

Матрица преобразования Уолша состоит из ортогональных векторов – столбцов равной дли-

ны и их собственных инверсий. Однако в общем случае ни преобразование инкрементного объединения, ни преобразование унифицированного разбиения не имеют ортогональных столбцов и поэтому мы должны ввести прямое и обратное преобразование явно.

Матрица унифицированного преобразования разбиения E c – это k -матрица, получаемая из матриц-ядер следующей формы:

⎡ 1 1 1 ... 1 ⎤ ⎢⎥ _⎢- 1 c _* - 1 - 1 ... - 1 _⎥

E ,c., = -- 1 c . - 1 ... - 1 .

^{c *} ⎢^⎢ : : : : : ⎥^⎥ ⎣- 1 - 1 - 1 ... c _* - 1 ⎥⎦

Такая матрица-ядро подсчитывает коэффициенты для единого гена. Можно неформально рассмотреть этот процесс. Первая строка суммирует все величины и делит на c *. число этих величин. Эта величина – коэффициент «средней величины» - e # . Все остальные строки являются отрицанием первой строки и содержат единственную дополнительную величину … . Она соответствует переопределению Z i = e # + e i , что дает e i = z i - e # .

Недвоичное преобразование разбиения, рассмотренное выше,является полностью достаточным для перехода от строкового представления к представлению, основанному на шаблонах. Кроме того,коэффициенты разбиения имеют более явное значение, чем коэффициенты Уолша или коэффициенты IC-преобразования [4]. В случае единственного гена инверсией матрицы IC является преобразование V J c¹ > , которое преобразует коэффициенты IC в значения строк Е^ >  со всеми отрицательными элементами,кроме элементов в первом столбце

< c * >

-1

Ic. -1

Здесь отражается различие в знаках между коэффициентами инкрементного объединения и унифицированного разбиения.Отметим,что инверсия этой матрицы,матрица IC-преобразования,имеет вид:

⎡1      1          1      ...      1

⎢⎥

⎢ 1   1 - c*     - 1     ...      1

V = -1            1 - c* ...     1

c* ⎢⎢:            :                  :             :             :

⎣1      1          1      ...   1 -c*

Аналогично преобразованию разбиения, формируем матрицы преобразования в общем виде с помощью операции ⊗:

V = v® v®...® v  v 1 = K-1 ® K-1 ® ®v^ Г c        y         x-/*“        •

Данная запись обобщает преобразование Уолша [4]. Являясь обобщением преобразования Уолша, IC-преобразование особенно интересно для исследования ГА. Преобразование Уолша ограничено двоичным представлением, IC-преобразование может быть применено с любым обобщенным (унифицированным) представлением. При использовании IC, в отличие от коэффициентов Уолша, теоретические результаты применимы к более широкому кругу представлений.

Заключение

Рассмотрены два родственных недвоичных преобразования – унифицированное преобразование разбиения, инкрементное преобразование объединения и их инверсии. IC-преобразование является обобщением двоично-ориентированного преобразования Уолша и упрощает обобщение ряда существующих теорий ГА для унифицированного представления. Матрицы IC-преобразования (и его инверсий) симметричны, в отличие от матриц унифицированного разбиения.

Преобразованиеобобщенногоразбиениявычисля-ет исключительно коэффициенты разбиения,необхо-димые для понимания свойств строк анализируемого шаблона,игнорируя избыточные подразумеваемые коэффициенты.Данное определение преобразования унифицированного представления дает возможность его применения в быстром преобразовании.