Универсальное уравнение времени перелета между двумя точками центрального поля тяготения

В работах [1] , [2] и [3] приведены различные варианты универсальных уравнений для расчета времени перелета между двумя точками центрального поля тяготения по эллиптическим, параболическим и гиперболическим орбитам. На возможность разработки единого уравнения для всех типов орбит указывалось также в [4] . При этом в [4] и [2] упоминалась необходимость в таких уравнениях смены знака большой полуоси и использования мнимых величин при расчетах времени перелета по гиперболическим траекториям по уравнению для эллиптических орбит.

Разработанные в теории орбитальных годографов [5] обобщенное уравнение перелета и уравнения связей углов, определяющих условия перелета, позволили найти принципиально новый подход к решению задачи определения времени перелета между двумя точками

Работа выполнена при финансовой поддержке проекта РФФИ № 12–07– 00205–а «Разработка новых способов решения задач управления движениями космических аппаратов на всех этапах полетов и оперативного отображения получаемых результатов на основе методов годографов и когнитивной графики».

○c М. Н. Бурдаев, 2012

○c ФГБУ «Научно-исследовательский испытательный Центр подготовки космонавтов имени Ю. А. Гагарина», 2012

○c Программные системы: теория и приложения, 2012

центрального поля тяготения и к отысканию нового универсального уравнения для расчета времени перелета по эллиптическим и гиперболическим орбитам. Один из вариантов такого уравнения для эллиптических орбит был опубликован в [6] . Несколько соотношений, полученных в [6] в процессе вывода основного уравнения, являются общими для всех типов орбит. Далее предлагается применить подход, использованный в [6] , для вывода уравнения времени перелета по гиперболическим орбитам.

Вывод универсального уравнения времени перелета между двумя точками центрального поля тяготения

Уравнение Ламберта для гиперболических орбит имеет вид lai

(1)       In - tM =—— [е (sh Hn - sh Нм ) - Hn + Нм ],

V^

где a — большая полуось гиперболической траектории перелета, е — эксцентриситет траектории перелета, Н — аналогичные эксцентрическим аномалиям эллиптических орбит величины.

В уравнении (1) и далее индексом "M" отмечены параметры орбиты в начальной точке перелета, индексом "N" — в его конечной точке.

Величина большой полуоси гиперболической траектории перелета вычисляется по формуле

_ тм a =2 - км ’ где тм —радиус-вектор начальной точки перелета, а обобщенный параметр км представлен уравнением годографа начальных скоростей перелета [4, 5]:

,  =     1 + ctg ² ^м   t А?

м ctg Фм - ctgA^M g 2 ’ фм —угол между тм и вектором начальной скорости перелета, А? — угол между тм и радиусом-вектором tn конечной точки перелета, Афм —угол между тм и направлением из точки М на точку N.

Величина угла Аф _м определяется из уравнения, приведенного в работе [5] :

cos А? — — ctg ^{А ф}м = ---. . - ™

.

sin Ат

Значения Н вычисляются по формуле

Н = 2 arth

Используя это соотношение, вычисляем разность Hn — Нм :

Hn — Нм = 2

е — 1   ^N е ■ I ' g 2

е — 1

е + 1

, #м\1

tg 2

= 2 arth f

( tg фм ctg ^

1) е sin д _м

)•

Решив совместно уравнения конических сечений для граничных точек М и N перелета и выполнив некоторые преобразования, получим соотношение е sin дм =

tg ^

1 - tg ф м ctg Афм •

Подставив его в (4) , находим:

Н И        ( ^ - ^{1 (1} - tg ^фм ctg ^Аф)

HN — Нм =2 arth ---7-  --~     --- у    (tg фм ctg ^^ — 1)

А»\ ctg ₂

= 2 arth ^И- \

- 1 (ctg фм - ctg Афм) ctg ^ - ctg фм

Ад\ ctg—).

Чтобы вычислить гиперболический синус sh Н, представим вели- чину Н в новом виде. Для ского тангенса:

этого используем формулу гиперболиче-

^{th Н}

н   _ е 2 — е

н е 2 + е

н

н

Решим это уравнение

относительно

е ^н — 1

⁼ е^н + 1 • е ^н :

е ^н

1 + th Н

1 -

th ^н •

Возьмем логарифм от этого выражения и подставим в него величину th Н :

1+th н

= ln

= ln

Н = ln      2

1 — th Н

Подставим полученные выражения для ен и Н в уравнение ги- перболического синуса:

sh Н =

е ^н

е

,-н

1 + th н

1 - th Н

1 - th Н

1 + th Н

)

2 th Н

1 - th ^{2 н}

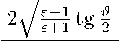
. 2 6

1 +1 tg^:

2Ve ² — 1 tg 2 cos ² 2

(e + 1) cos ² 6 — (e — 1) sin ² 6

V e ² — 1 sin 1

e ( cos ² 2 — sin ² 6 ) + cos ² 2 + sin ² 6

Ve ² — 1 sin 1

1 + e cos 1

V e ² — 1 e sin 1 e (1 + e cos 1)

¹ ve ²

e

1ctg Ф,

откуда следует e sh Н = Ve2 — 1 ctg ф

и

• (6)       e sh H _N — e sh Нм = V e ² — 1 (ctg - _N — ctg фм ) .

Величина ctg -n определяется из соотношения [ ] :

ctg -n — ctg фм =

(^м+0(

Д1

ctg 2

ctg -фм^

Д1

^2ctg^ .

С этой подстановкой соотношение (6) принимает вид

• (7)    e (sh H _N — sh Н _м ) = Ve ² — 1 x

  x

  
  

  [(™ ^{+ 1}X^ct8T ^{— ctg фм}) ^{—     Д}-

  
  

Подставляя (2) , (3) , (5) и (7) в (1) , получаем

(8) t n — tM = ~X= v^

______ гм

(1+ctg ² ф м )tg ^ ctg ^ M - ctg Дф м

X

x | V ^{2 - 1} [ (^ +1) (ctg ^ ^{- ctg фм}) ^{- 2} ctg ^] ^-

- ’«th (v^      t   ^)} •

Границы фм , разделяющие диапазоны углов фм для эллиптических и гиперболических траекторий перелетов, определяются из уравнения (3) для условия км = 2. Решив его относительно фм , получаем

" Д^ I гм (    _2 Д^ \ фМ 1,2 = arcctg

■ ^TN (1 + ctg т)

Углы ф _м соответствуют параболическим траекториям перелетов.

Между двумя значениями фМ решений этого уравнения заключен диапазон величин углов фм для эллиптических траекторий перелетов. Меньшие значения углов фм свойственны гиперболическим траекториям, не приходящим в заданную конечную точку N перелета. Большие значения углов фм соответствуют гиперболическим траекториям, по которым перелеты в заданную конечную точку возможны.

Максимальное значение угла фм для гиперболических траекторий теоретически равно величине угла Дфм ■ Этому случаю при конечных значениях величин начальных радиусов гм перелетов соответствуют бесконечные величины км и начальных скоростей перелетов, что противоречит действующим законам физики. Поэтому максимальный возможный угол фм для перелетов по гиперболическим траекториям ограничен максимальной предельной скоростью перелета, равной скорости света.

В статье [6] приведено в сокращенном виде аналогичное уравнение времени перелета для эллиптических орбит: используя формулы

(7), (10), (12), (13), (17) и (18) статьи [6], это уравнение можно пред ставить в виде

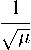
______ тм ______

2 _— (1+ctg ² Фм ) tg ^ ctg ^ M - ctg Д ф м

- И м MXхм X] —

_(ТМ⁺¹ ) ( ^ctg ^r ^{— ctg} ) ^{— 2ctg}ir ]} ■

Сопоставление уравнений (8) и (9) обнаруживает, что они, как и указывалось в [2, 4] , различаются знаками больших полуосей и выражения (1 — е ² ) , а также присутствием функции arctg в формуле для эллиптических орбит и функции arth в формуле для орбит гиперболических.

Необходимость смены знаков в выражениях для большой полуоси, для разности (1 — е ² ) под корнями в правой части уравнений (8) и (9) и смены знака правой части уравнений при переходе от расчетов для эллиптических орбит к расчетам для гипербол легко устраняется введением операции вычисления модуля для указанных элементов уравнений. После этого различие между уравнениями (8) и (9) остается только в обратных функциях в их правых частях.

Величина эксцентриситета е траектории перелета вычисляется для обоих уравнений по единой формуле, приведенной в работе [7] :

Е=\М+

км (км ^{— 2)}

1 + ctg2 фм ’ откуда

Vi e ² — 1 | =

^к М ^{( к} м ^{— 2)} 1 + ctg ² фм

.

В итоге универсальная формула получает вид

(10) t _N — t _M =

tm

V^

(1+ctg ² ф м )tg ^2 ^ ctg ф м - ctg Д ф м

— 2

X | , 1 72| ( (TM + i) (ctg ^ _ ctg ^^) _ 2^ctg ^ _

A^l ) ctg 2

— 2 ar

( ctg А   /Й---21 ctg ^M — ctg A^M

(-                ctg ^2^ — ctg ^M где в символе обратной функции в правой части уравнения верхнее сочетание букв выбирается для эллиптических орбит, нижнее –– для гиперболических орбит.

При выполнении расчетов на современных электронных вычислительных машинах в универсальном уравнении действует для эллиптических орбит условие проверки и коррекции алгоритма расчетов, отмеченное в статье [6] : если при вычислениях появляется величина En — Em , меньшая нуля, то в правую часть уравнений (8) - (10) следует добавить 2тт. В уравнениях (8) и (9) знак этой разности определяется и совпадает со знаком разности ctg ^2^ — ctg ^м.

Заключение

Материал статьи является продолжением исследований, начатых автором в работе [6] . Полученные результаты используются в ФГБУ «Научно-исследовательский испытательный Центр подготовки космонавтов имени Ю. А. Гагарина» для обучения космонавтов теории перелетов.