Универсальный программно-аппаратный комплекс для анализа спектров электрических и оптических сигналов

Объектом проведенного исследования являются алгоритмы обобщенного линейного спектрального анализа электрических и оптических сигналов. Цель работы – разработка аппаратной и программной частей устройства, предназначенного для спектрального анализа электрических и оптических сигналов.

В процессе работы проводилось предварительное моделирование алгоритмов спектрального анализа на языке Matlab, затем программы и подпрограммы переводились на язык С++ с целью ускорения вычислений, что необходимо для обработки электрических и оптических сигналов в реальном масштабе времени.

Были реализованы алгоритмы и программы вычисления следующих видов линейных спектров:

– классический Фурье-спектр с различными окнами – прямоугольное, модифицированное окно Ханна, треугольное окно Барлетта, Кайзера [1];

• –    спектр сигнала в базисе Уолша (базисные функции упорядочены как по Уолшу, так и по Адамару) [2; 3];

• –    спектр сигнала в базисе Хаара [2];

  – спектр сигнала в модифицированном ортогонализированном базисе функций типа «Мексиканская шляпа» (Mexican Hat) [4]; обычный базис такого вида не является ортогональным, что существенно усложняет процедуру цифрового спектрального анализа; поэтому базис был предварительно ортогонализирован с помощью процедуры Грама – Шмидта [5].

В результате исследования впервые был создан макет устройства спектрального анализа электрических и оптических сигналов, предназначенный для научных исследований и для использования в учебном процессе обучающихся радиотехническим специальностям. Опишем вкратце особенности программной реализации алгоритмов спектрального анализа.

Особенности программной реализации Фурье-анализа

Аппаратная часть анализатора, которая подробнее будет описана ниже, предполагает, что каждый сигнал, поступающий на вход двухканального АЦП, представляет собой действительную и мнимую части комплексного сигнала. Сигналы звукового диапазона поступают на вход устройства непосредственно в виде двух отдельных сигналов, а высокочастотные сигналы радиочастотного и оптического диапазонов преобразуются в комплексный сигнал с помощью квадратурного расщепителя, который для оптических сигналов чаще называется оптическим гибридом.

При этом при вычислении Фурье-спектра этих независимых сигналов для ускорения процедуры применен следующий подход: входные последовательности отсчетов сигналов x ( к ) и y ( к ) считаются, соответственно, действительной и мнимой частями комплексного сигнала z ( к ) = = x ( к ) + iy ( к ) .

После вычисления отсчетов спектра с применением одной процедуры быстрого преобразования Фурье (БПФ) этого сигнала Z ( m ) = = Z x ( m ) + i Z y ( m ) из этой функции можно получить действительные и мнимые части спектров сигналов S_x ( m ) , S y ( m ) и U x ( m ) , U y ( m ) с помощью простых выражений:

Sx (m ) = [ Zx (m) + Zx (N - m +1)] /2; (1) Sy (m) = [Zy (m)- Zy (N - m +1)]/2; (2) Ux (m) = [Zy (m) + Zy (N - m +1)]/2; (3)

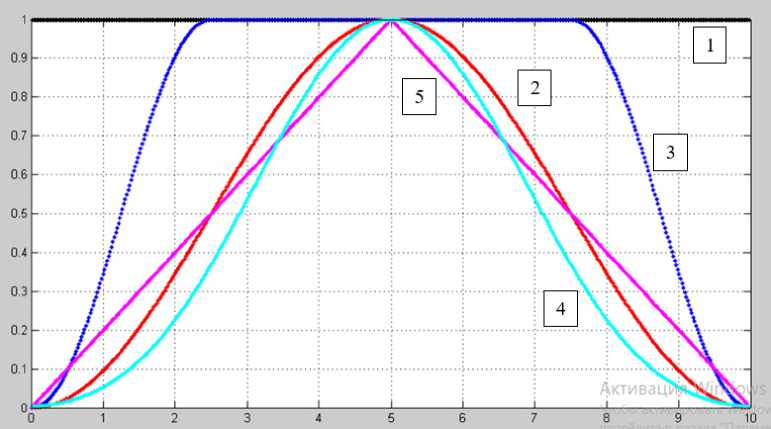
Рисунок 1. Графики окон, используемых при Фурье-анализе: 1 – прямоугольное; 2 – окно Ханна («hanning»); 3 – модифицированное окно Ханна; 4 – окно Кайзера; 5 – треугольное окно Барлетта

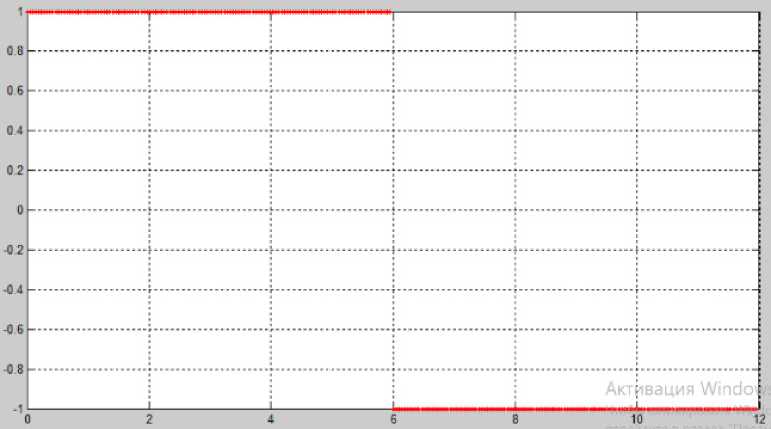
Рисунок 2. Базисная функция Уолша (Walsh) (1)

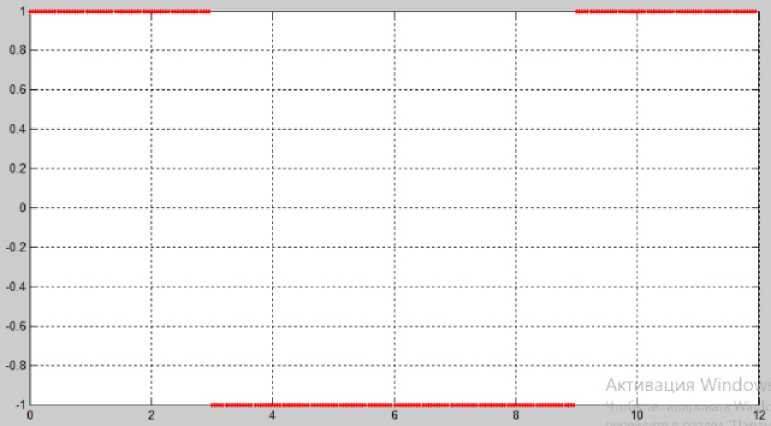
Рисунок 3. Базисная функция Уолша (Walsh) (2)

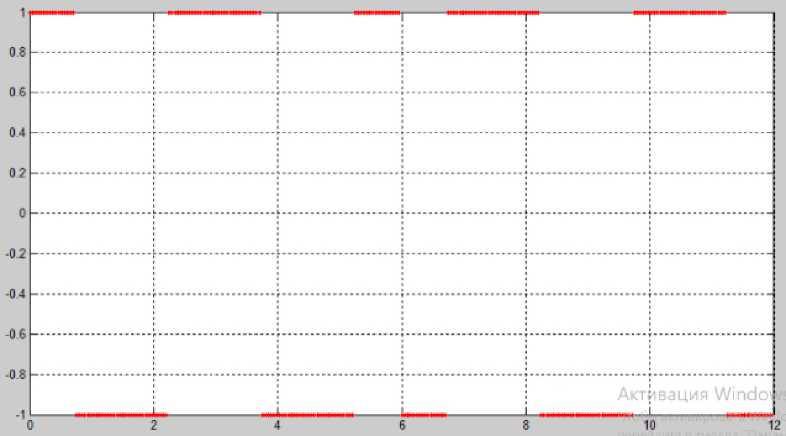
Рисунок 4. Базисная функция Уолша (Walsh) (9)

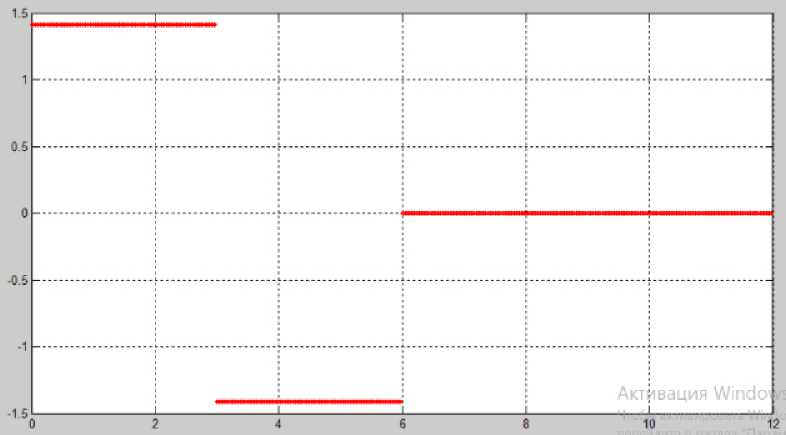
Рисунок 5. Базисная функция Хаара (HAAR) (2)

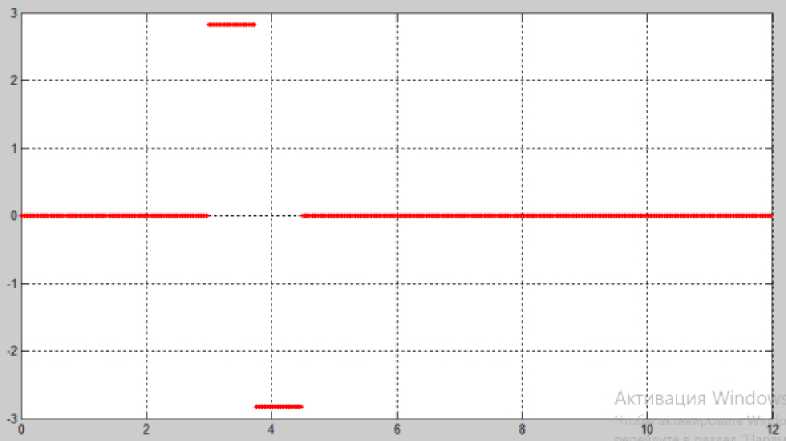
Рисунок 6. Базисная функция Хаара (HAAR) (10) «Infokommunikacionnye tehnologii» 2022, vol. 20, no. 1, pp. 90–102

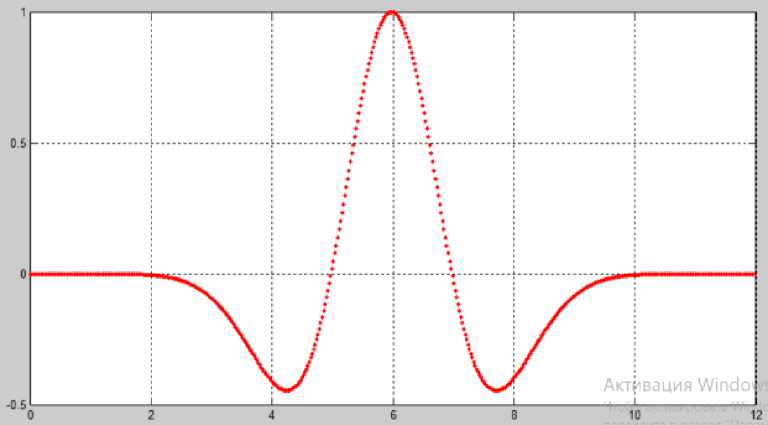
Рисунок 7. График материнского вейвлета «Мексиканская шляпа»

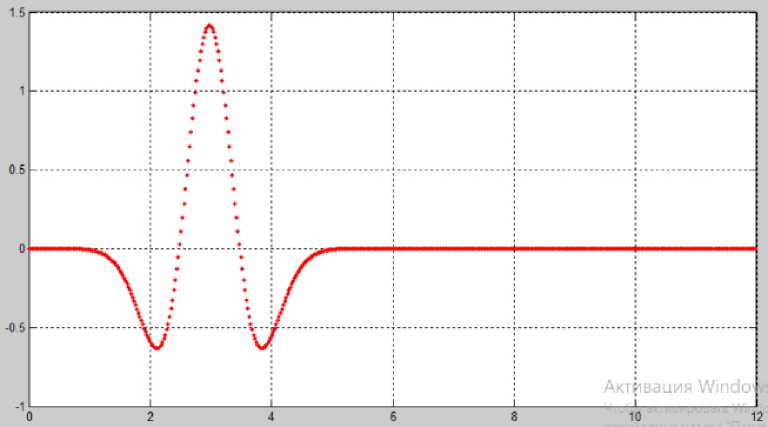
Рисунок 8. График дочернего вейвлета «Мексиканская шляпа» (MHAT) (2)

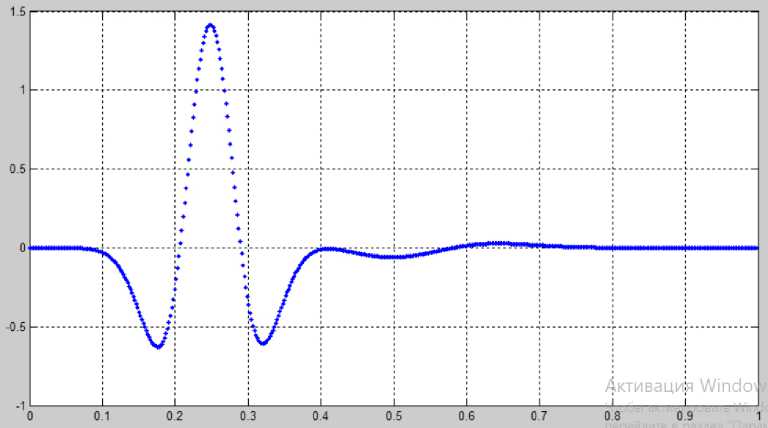
Рисунок 9. График дочернего вейвлета «Мексиканская шляпа» (MHAT) (2) после ортогонализации с помощью процедуры Грама – Шмидта

Uy (m) = -[Zx (m) - Zx (N - m +1)]/2.   (4)

Графики окон, используемых при Фурье-анализе, представлены на рисунке 1.

При формировании окна Кайзера

I 0

W k ( n ) =

P 1

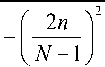
1 0 ( P )

выбран параметр p = 8 и применен известный рекуррентный алгоритм вычисления модифицированной функции Бесселя 1 ₀ ( x ) [1]:

to

10 (x)=1+E k =1

( x / 2) k

k

Особенности программной реализации алгоритмов обобщенного спектрального анализа

Базисы Уолша и Хаара являются классическими [2; 3]. Некоторые из базисных функций пред- ставлены на рисунках:

Вейвлет-базис функций типа «Мексиканская шляпа» (Mexican Hat), так же как и другой вейвлет-базис [4], формируется путем задания так называемого материнского вейвлета V(t), а остальные базисные функции, т. е. дочерние вейвлеты, формируются путем его временного сжатия, сдвига по времени и изменения амплитуды в соответствии с выражением:

1    (t—

Vs Ttt) = -=V| —I.          (7)

⁵ , T

V o V ° )

Материнский вейвлет типа «Мексиканская шляпа» (Mexican Hat) определяется как вторая производная от гауссовской функции x     d2

V(t) =   ,   exP dt2

t ²

—

t ²

= (1 - 1 ² ) exp

График этого материнского вейвлета приведен на рисунке 7.

Как было отмечено выше, обычные базисные функции типа «Мексиканская шляпа» не являются ортогональными (а только линейно независимыми), что существенно усложняет процедуру цифрового спектрального анализа, поэтому базис был предварительно ортогонализирован с помощью процедуры Грама – Шмидта [5]. Преобразование исходных базисных функций V i в ортогональные Ф i производится в соответствии с алгоритмом:

Ф1 =V,;

m - 1 V Ф

Ф m =V m-X} / ,„. k) Ф k, m = 2,3... N. (9) n=1 (Ф k , Ф k )

Указанная процедура немного изменяет вид базисных функций. Эти изменения очень слабо влияют на результат спектрального анализа, но при этом существенно упрощается и ускоряется процедура спектрального анализа. Для примера на рисунке 9 приведен график предыдущего дочернего вейвлета после ортогонализации с помощью процедуры (9). Очевидно, что форма этих базисных функций отличается незначительно.

Реализация цифрового программноаппаратного комплекса для обобщенного анализа спектров электрических и оптических сигналов

Аппаратная часть анализатора состоит из трех основных блоков: низкочастотный, высокочастотный, процессор управления. Принципиальные схемы блоков представлены на рисунках 10–12 соответственно, внешний вид устройства – на рисунке 13, спектры сигналов – на рисунках 14 и 15.

Низкочастотный блок состоит из двух аналоговых каналов с полосой пропускания 20 кГц каждый и одного канала синхронизации. В каждый аналоговый канал входят входные цепи, предназначенные для выделения переменной составляющей входного сигнала на элементах R1–R6, C1–C2, защиты от перенапряжения на элементах VD1–VD4, согласования высокого входного сопротивления схемы с последующими каскадами схемы на IC1 NE5532, фильтрации помех питающих напряжений на элементах R7–R8, C3–C4. После прохождения входных цепей сигнал поступает на управляемый аттенюатор/уси-литель на IC2 PGA2311, позволяющий регулировать входной сигнал в пределах –95,5…+31,5 dB с шагом 0,5 dB независимо в каждом канале по цифровому управляющему каналу. На элементах R9–R11, C5–C7 собрана схема фильтрации помех питающих напряжений. Далее нормированный входной сигнал поступает на фильтры низких частот на элементах R12–R17, C8–C13, IC2 NE5532 для ограничения полосы входного сигнала значением 20 КГц. На элементах R18–R19, C14–C15 собрана схема фильтрации помех питающих напряжений. Канал синхронизации предназначен для согласования управляющего сигнала и аналоговых сигналов во временной области и собран на элементах R31, R101, R102, C24, U1 74LVC1G04.

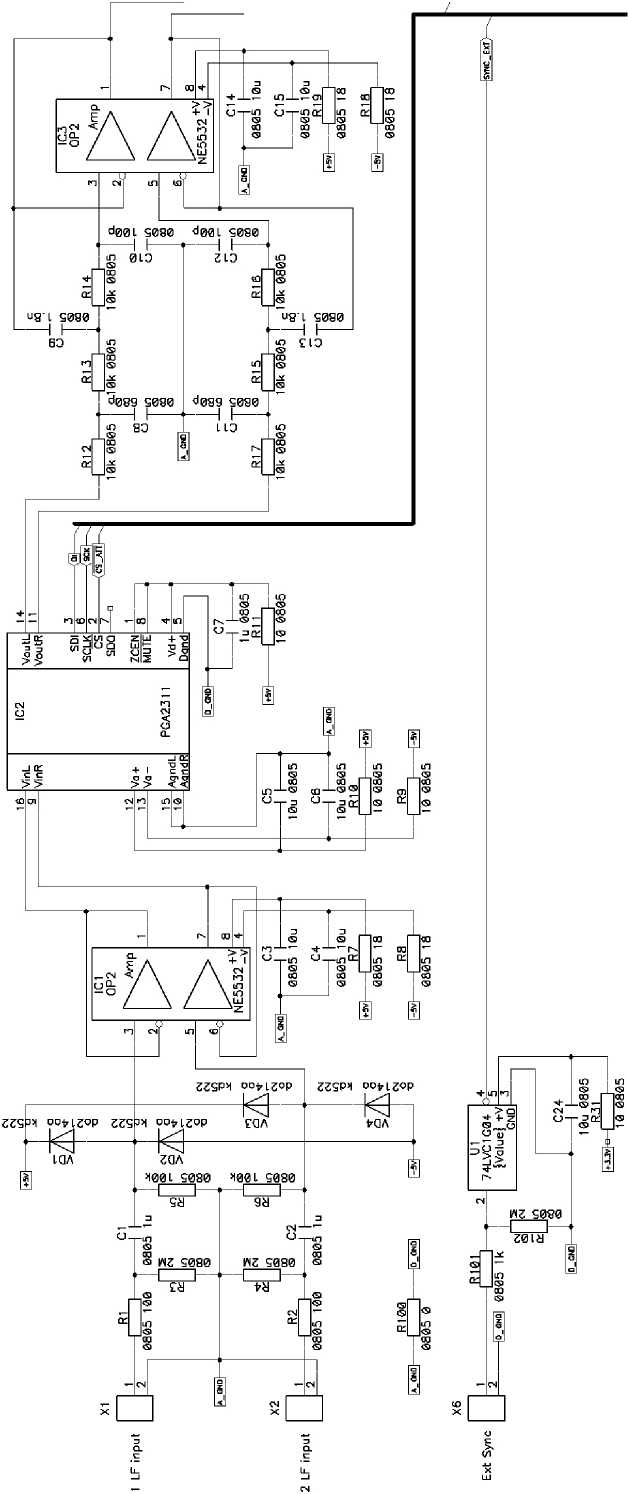
Рисунок 10. Принципиальная схема НЧ-блока с опорным генератором на частоту 500 МГц (для ВЧ-блока)

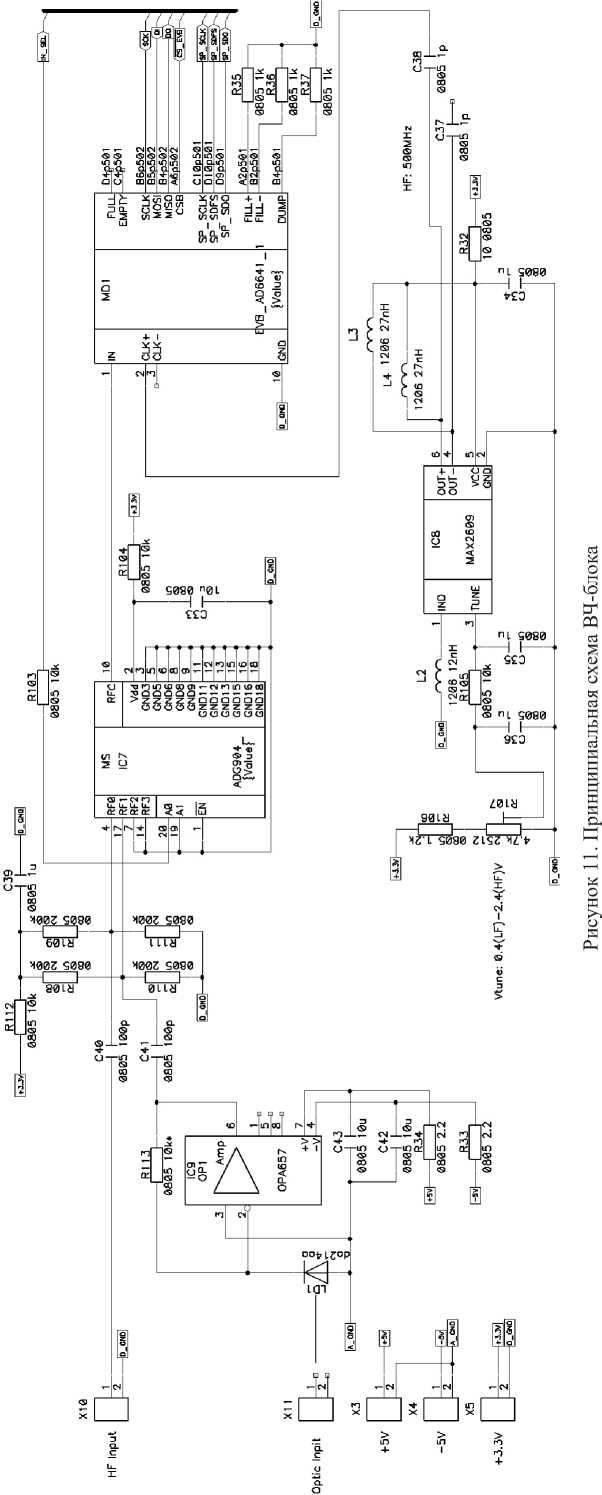
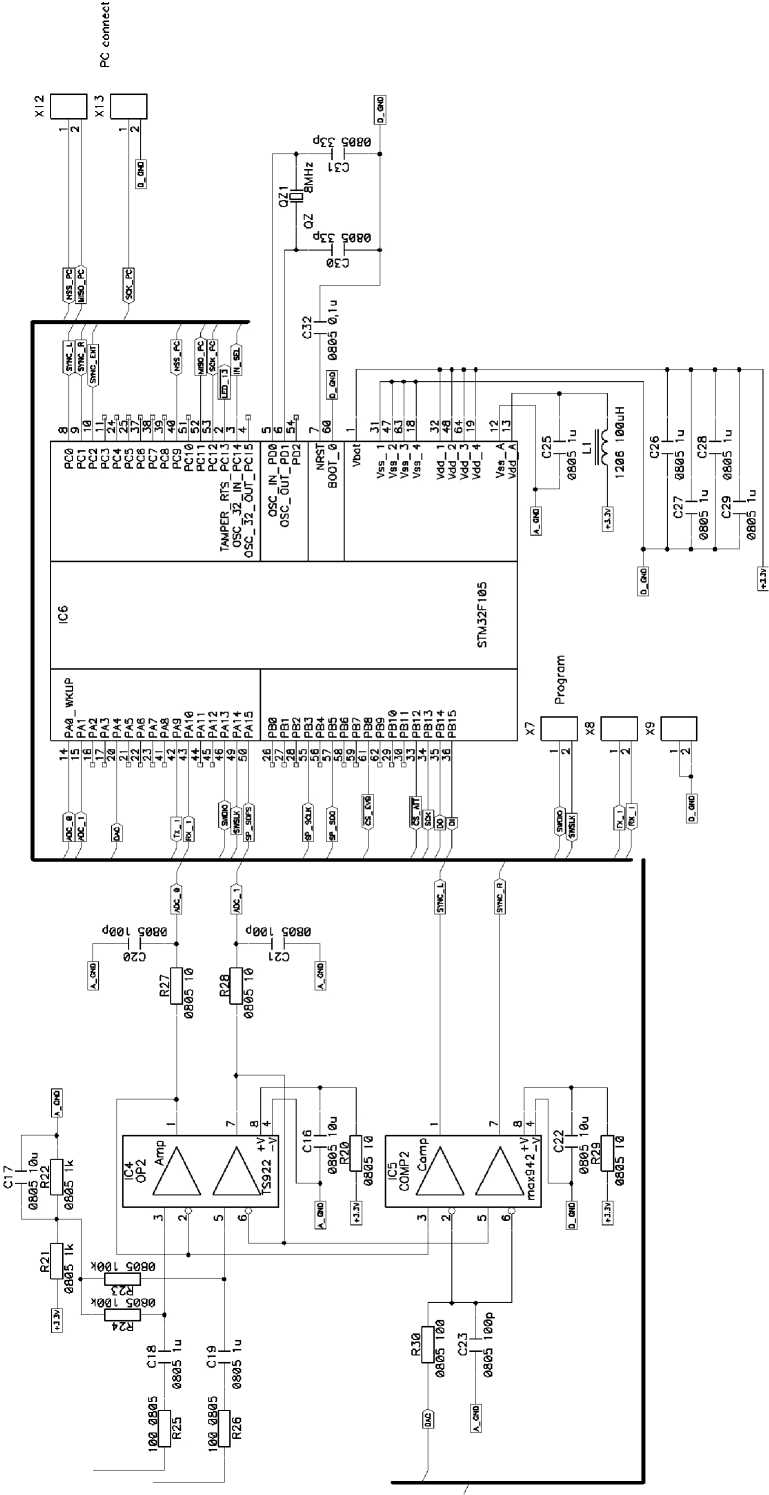
Рисунок 12. Принципиальная схема центрального процессорного устройства (ЦПУ) и блока сопряжения с микрокомпьютером

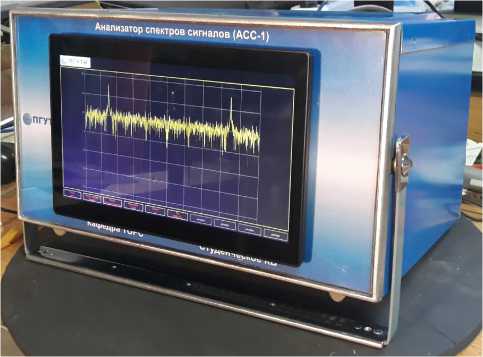
Рисунок 13. Общий вид анализатора спектра

Высокочастотный блок состоит из РЧ-канала и канала оптического диапазона, ВЧ коммутатора, АЦП, генератора тактового сигнала АЦП. В РЧ-канал входят элементы для выделения переменной составляющей сигнала C40 и установки смещения для коммутатора с целью увеличения динамического диапазона анализируемого сигнала R109, R111. Канал оптического диапазона предназначен для преобразования оптического сигнала в ВЧ-сигнал для последующего анализа и собран на элементах LD1, R13, R108, R110, C41, IC9 OPA657. На элементах R33, R34, R112, C39, C42, C43 получена схема фильтрации помех питающих напряжений. ВЧ-коммутатор предназначен для выбора либо РЧ-канала, либо канала оптического диапазона для анализа. ВЧ-коммутатор создан на R103, IC7 ADG904. На элементах R104, C33 собрана схема фильтрации помех питающих напряжений. АЦП предназначен для аналогоцифрового преобразования входных сигналов в цифровые отсчеты анализируемого сигнала. АЦП разработан на модуле AD6641 Eval Board с частотой дискретизации 500 МГц, разрядностью 12 бит и буфером в 16 тысяч отсчетов. Модуль управляется по цифровому управляющему каналу. Генератор тактового сигнала АЦП предназначен для формирования сигнала дискретизации с частотой 500МГц, собран на R105-R107, C35-C36, L3, L4, IC2 MAX2609. На элементах R32, C34 создана схема фильтрации помех питающих напряжений.

Процессор управления предназначен для управления процессами записи входных анализируемых сигналов. Низкочастотные сигналы подаются на схему смещения уровня входного сигнала для согласования уровней АЦП на элементах R21-R28, C18-C21, IC2 TS922. Далее низкочастотные сигналы подаются на выводы 14,15 АЦП в микросхеме IC6 STM32F105, где преоб-

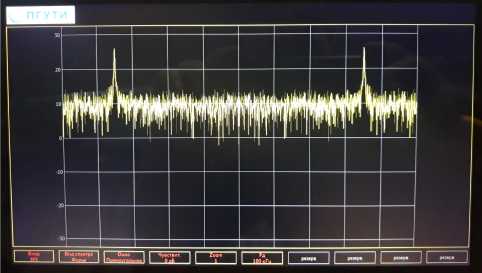
Рисунок 14. Амплитудный спектр по Фурье бигармонического сигнала на экране анализатора

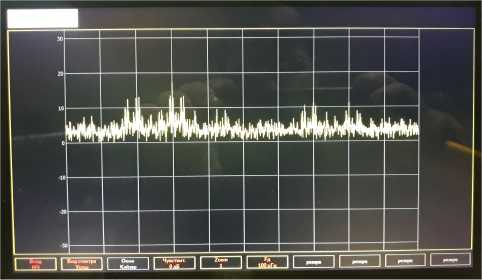
Рисунок 15. Спектр Уолша бигармонического сигнала на экране анализатора разуются в 12-битные отсчеты и записываются во внутреннюю память. Низкочастотные сигналы подаются на компаратор синхронизации на IC5 MAX942, где сравниваются с напряжением установки, которая формируется на выводе 20 IC6. Сформированные сигналы синхронизации каналов поступают на выводы 8, 9 IC6. Сигнал внешней синхронизации – на вывод 10 IC6. Сигналы управления аттенюатором/усилителем снимаются с выводов 33–36 IC6. Сигналы управления модуля AD6641 Eval Board – с выводов 50, 55, 57, 61 IC6. Сигналы управления коммутатором снимаются с вывода 3 IC6. Для передачи данных из IC6 на внешние устройства используется канал передачи данных на выводах 40, 52, 53. Для обмена командами c внешними устройствами используются выводы 42, 43 IC6. Микросхема IC6 тактируется кварцевым резонатором QZ1 с частотой 8 МГц. На элементах R20, R29, C16, C22, C25–C29, L1 собрана схема фильтрации помех питающих напряжений. Блоки питаются напряжениями +3,3В, +5В, –5В.

Заключение

В заключении хотелось бы отметить, что реализованный и описанный программно-аппаратный комплекс, предназначенный для изучения различных спектров сигналов, является достаточно гибким в смысле расширения его функциональных возможностей и параметров. Совершенствование его возможностей на аппаратном уровне заключается в расширении не только частотных и динамических диапазонов исследуемых спектров электрических и оптических сигналов в смысле Фурье-анализа, но и его функциональных возможностей. Добавление номенклатуры программ анализатора позволит не только расширить число исследуемых линейных спектров, но и реализовать анализ практически любых характеристик сигналов, как детерминированных, так и случайных, например исследование корреляционной и ковариационной функций [6], энергетического спектра, кепстров [7], а также нелинейных спектров задач для уравнений Кортевега – де Фриза [8; 9], нелинейного уравнения Шрёдингера [10; 11], уравнения sin-Гордона [8], модифицированного уравнения Шрёдингера (уравнения Габитова – Турицы-на) [11], Бюргерса [8] и многих других.