Unsupervised color texture segmentation based on multi-scale region-level Markov random field models

Acknowledgments : This work was financially supported by the Key Technology Projects of Henan province of China under Grant 15210241004, Supported by Program for Changjiang Scholars and Innovative Research Team in University, the Key Technology Projects of Henan Educational Department of China under Grant 16A520036, the Key Technology Projects of Henan Educational Department of China under Grant 16B520001,the National Natural Science Foundation of China under Grant 41001251, Anyang science and technology plan project: Researches on Road Extraction Algorithm based on MRF for High Resolution Remote Sensing Image, and the Research and Cultivation Fund Project of Anyang Normal University under Grant AYNU-KP-B08.

In the past decades, fuzzy clustering algorithms have been widely used in image segmentation. because they have robust characteristics for ambiguity and are able to retain more original image information than hard or crisp segmentation methods.Besides, they requires experts with adequate domain knowledge to determinate the number of clusters before clustering, which greatly limits their application.

The Markov random field models (MRF) have a perfect theoretical basis and can easily describe the spatial information of the image. So, they have a wide application in the field of image segmentation [7]. In the Bayesian framework, the MRF model based on pixels can integrate spatial interaction between pixels into the tagged verdict through the form of a priori probability, which can obtain better regional segmentation results. However, in the segmentation of texture images, especially macro texture images, it is difficult to accurately describe the characteristics of different textures through the spatial relationship between pixels. So, a larger scope of spatial interactions should be used to obtain accurate segmentation results. S. P. Chatzis and T. A. Varvarigou explored the spatial coherency modeling capacities of the hidden

Markov random field (HMRF) model in the fuzzy clustering procedure and proposed the HMRF-FCM algorithm [8]. We extended this method into a multi-scale version by capturing and utilizing the multi-scale spatial constrains [9] and enhanced its accuracy of selecting local information by incorporating region-level information into the fuzzy clustering [10]. The region-level MRF (RMRF) [11] models introduce the interregional interaction into the image segmentation, which will make full use of the larger scope of the image space information. However, the RMRF model on a single scale does not take into account the non-stationary characteristics of the image itself, which will seriously affect its stability.

In this study, we present a multi-scale RMRF modelin wavelet domain (MsRMRF), On the basis of wavelet decomposition for the compensation of the inability of image non-stationary characterization the MsRMRF makes full use of the regional spatial interaction between different scales to get the exact texture description.

The reminder of this paper is organized as follows: in Section 2, we provide a brief review of the region-level markov random field model. In Section 3, we introduce our algorithm based on multi-scale region-level Markov random field models. The experimental results of the proposed approach are given in Section 4. Finally, Conclusions are drawn in Section 5.

• 2.    Region-level Markov random field model

Suppose S = {1, 2, ..., N } represents pixel index assemblage of pending image Y . Y₅ ( 5 e S ) represents the B dimensional pixel color vector on the position s . In the initial segmentation, there are M different regions corresponding to the image Y . These regions and their spatial relationships can be described by the Region Adjacency Graph (RAG). Suppose that RAG is recorded as G = { V , E }. In this set, V represents the set of vertices, and E represents the set of edges. Each vertex v e V represents an area in the initial segmentation, which connects region v 1 and region v 2 , and their spatial interactions are represented by the edges e 1,2 e E . A regional set of adjacent relations forms a neighborhood system n = { n _v I v e V} at a regional level. n _v represents a set of regions that have side connections with the region v . Suppose that the image Y is divided into K categories, and all the pixels of the same region are the same tagged symbol as the region, then the segmentation result X can be represented as a RMRF tagged field: X = { X_v | v e V }, X_v = { X₅ 1 5 e V }(1 < X_v < K) represents the category markers of region v . Meanwhile, it also represents the category markers of all the pixels in region v .

In the Bayesian framework, the segmentation model [12] based on RMRF can be expressed as:

X = argmax x { P ( X ) P ( YX ) } , (1)

P ( Y | X ) is regional class conditional probability and P ( X ) is regional priori probability.

Assuming that every class is subject to Gauss segmentation and the class condition is independent, then P ( Y | X ) can be expressed as:

P ( YX ) = П v. P ( Y -I ^X - ) •                   (2)

P ( Y_v | X_v ) the class conditional probability of the region v , can be expressed as:

ц _X . and S _X . represent the mean vector and covariance matrix of class X v respectively. Gaussian distribution P ( Y_s | X 5 ; ц x_v . S x_v ) can be expressed as:

P ( Y|X ; ц x .

^E ' ' ) = ( 2 - )"p x - Г ^X

⁽ Y - ^ц X v ) ' E x¹. ⁽ Y - ^ц X v )

x exp 1 -

.

A priori model P ( X ) can be expressed by the Gibbs distribution:

P ( X ) = 1exp { - U ( X )/ T } .                   (5)

Z = E x exp {—U (X) !T} is a normalization constant, and

^U ( ^X ) = X„ .„ £ , .„е ( v . v ' )

is an energy function. In this paperwe only consider the interaction between two adjacent regions, so Q ( v , v' ) is defined as:

Q ( v , v ‘ ) =

= ( 1- 5 ( X v , X v - ) )

a v      b v , v

IЦ v -Ц v 'I b v

a_v , b_v and ц _v represent the area, edge length and color mean vector of the region v respectively. b v , v' is the common boundary length of region v and v' . 5 ( X_v , X_v ), which is the delta function, can be expressed as:

5( X , X_v ) = J ^{1, Xv} = ^Xv ' ^,                         (7)

^{( v}’ ^v ) [ 0, X v * X v - .

The formula (1) is equivalent to the formula (8):

X = argmin x { - log ( P ( X ) ) - log ( P ( Y|X ) ) } .    (8)

The corresponding energy function E can be expressed as the sum of the marked field energy function E X =–log( P ( X )) and the characteristic field energy function E Y =–log( P ( Y | X )):

E = E_x + E Y .

The minimum energy segmentation result is the optimal segmentation result. The following formula can be achieved by putting formula (2) and (5) into formula (8):

E =

Z veV { Z v e V [ ( Y s - Ц a ) ' Z X ( Y s

-Ц X v ) + log ( ^Z X v |) ]^Z s e v ^+Z v 'en ,

( 1 -5 ( X v , X v- ) )

a v       b v , v ’

I Ц v — Ц v 'I bv

The minimization of the energy function can be solved by the optimization algorithm, such as the Iterative Conditional Modes [13], the Expectation Maximization (EM) [14], the Gibbs [15] sampling and the Graph Cut (GC) [16].

Though image segmentation based on RMRF model can take into account the large range of spatial information through a priori probability function at the region level, the model only describes the statistical characteristics of the image on a single spatial resolution scale, which is obviously incompatible with the non-stationary characteristics of the image, and needs to be improved.

• 3.    Multi-scale Region-level Markov Random Field Model

In order to improve the RMRF segmentation model, we put forward a multi-scale RMRF model (MsRMRF) in wavelet domain. Suppose the image Y is decomposed into D scale, and the corresponding wavelet coefficient is expressed as W ={ w ^d |1 <  d <  D }. w d = { w d | s e S^d } represents the image of the wavelet coefficients vector on the scale d . S ^d is the pixel position index set on the scale d . The wavelet coefficients vector on each scale can be expressed as:

wd =

_ f[ w d ( LL ), w d ( LH ), w d ( HL ), w d ( HH ) ] ' , d = D , (11) [[ w d ( LH ) , w d ( HL ) , w d ( HH ) ]' , d * D .

If the scale corresponding to the original image is recorded as d =0, that is to say w ⁰= Y , then there are multi-resolution data with ( D + 1) scales altogether. Assuming that the RAG obtained by the initial segmentation on the scale d is expressed as G ^d = { V ^d , E ^d }, the corresponding neighborhood system is expressed as n d ={ n d I v e V^d }, and then the segmentation results on each scale can be expressed as a RMRF tagged field on the scale: X d = { X d | v e V^d }. X d represents the common marks of the pixel set { s | s e V^d }on the scale d . The tagged field on all scales consists of a multi-scale tagged set X ^ms ={ X^d | d =1, 2, ..., D }.

In the Bayesian framework, segmentation model based on MsRMRF can be expressed as:

X^ms = argmax _X m { P ( W^X^ms ) P ( X^ms ) } . (12)

P ( W | X ^ms ) represents multi-scale class conditional probability, and P ( X ^ms ) represents multi-scale priori probabilities.

If the class condition is independent, then the P ( W | X ^ms ) can be expressed as:

P ( W I X " ) = П D =0 П v , V d P ( w i\ X i ) . (13) w_v^d represents a set of wavelet coefficient vectors corresponding to region v on the scale d . If it obeys the

Gauss distribution, the regional conditional probability density P ( w v ^d | X v ^d ) can be calculated by the following formula:

P ( w d I X d ; v e V d ) =

= П s e v ^P ( w d | ^X vd ^; ^ X v , ^Z X d ) .

If the segmentation results of high resolution scale are affected only by the segmentation results of adjacent low resolution scale, then the multi-scale priori probability P ( X ^ms ) can be expressed as:

P ( X^ms ) = P ( X^D ) П Dd’_o P ( X ^d\ X^{d + 1} ) .            (15)

It’s hard to get a complete expression of P ( X ^d | X ^{d +1}), so we describe the dependencies between scales by using X ^{d +1} to provide initial tags for X ^d . The image segmentation algorithm based on MsRMRF model can be decomposed into the combination of RMRF segmentation for each scale, and can transfer the correlation between scales through tagged results of the scales. On the minimum resolution scale, we use the pixel level ICM algorithm to obtain the segmentation results. On other scales, the segmentation results are obtained by the minimum energy function expressed by the formula (16).

E d = Z veV { Z s e v [ ( w d —Ц X d )' Z X d ( Y s —Ц X d ) +

⁺ log (| ^Z X d |)] ^{+                                       (16)}

+ Z

v 'en d

(1 -s c X v , X d- ))

a v b v , v' IЦ v -Ц v 'I b v

In this paper, the Mean Shift (MS) algorithm is used to obtain the initial region of each scale. The segmentation process is shown in Figure 1. The specific segmentation algorithm is as follows:

Step 1 : Input image Y , set the class number K and wavelet decomposition scale D , MS segmentation of the minimum area ar , space bandwidth h_s and range bandwidth h_b .

Step 2 : Carry out D scale wavelet transform for image Y , obtain the initial region of the scale based on the low frequency component w ( LL ) on each scale, set up RGA and calculate the area a v , the edge length b v , and the color mean ц _v of each region.

Step 3 : Execute pixel level ICM segmentation on scale d = D , and obtain the segmentation results X^D .

Step 4 : Let d = d + 1. If d <0, the algorithm operation stops. Then output the segmentation results on the scale d + 1 as the final result; otherwise, turn to step 5.

Step 5 : Project the segmentation results on the scale d + 1 to the current scale X ^{d + 1}, and use the voting method to get the segmentation tags in each region of the current scale.

Step 6 : Adopt the ICM algorithm optimal formula (16) to obtain the segmentation results X ^d . Turn to step 4.

• 4.    Experimental analysis

In order to verify the effectiveness of the algorithm, a combination of color texture images and two remote sensing images are used in this paper. And the algorithm proposed in this paper has been compared with the methods in ICM, MRMRF [17] and literature [18]. ICM is a classic single scale MRF segmentation algorithm, MRMRF is a multi-scale segmentation algorithm in wavelet domain, and the method in literature [18] is a single scale RMRF segmentation algorithm. In the experiment, both MRMRF algorithm and the algorithm proposed in this paper use 3-scale haar wavelet transform.

The algorithm proposed in this paper is compared with that of MRMRF, which is used to verify the ability of the wavelet domain MsRMRF segmentation algorithm proposed in this paper in accurately describing the texture characteristics by using a wide range of spatial information. Meanwhile, the algorithm proposed in this paper is also comparing with the method in literature [18], which is used to verify the ability of this algorithm in using multi-scale information and in describing the nonstationarity of the image. Besides, the MS algorithm used in this algorithm uses a set of fixed parameters: ar = 10, h s = 6, h b =6.

Input image

Wavelet transform

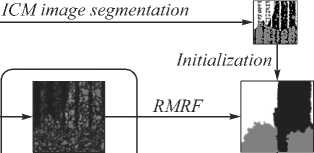
Mean Shift Clustering

Multi-scale image segmentation

Fig. 1. The segmentation process based on the MsRMRF model in the wavelet domain

segmentation results of ICM, the third column is the segmentation results of MRMRF, the fourth column is the segmentation results of literature [18], and the fifth column is the segmentation results of MsRMRF

Synthetic texture images are shown in the first column in Figure 2. (a1), (b1) and (c1) in Figure 2 are obtained by Prague texture segmentation data generator [19]. (d1) in Figure 2 is manually synthesized by using remote sensing image texture. The class numbers of four images are 5, 4, 3 and 4 respectively. The segmentation results of ICM algorithm, the MRMRF algorithm, the method in literature [18] and the algorithm proposed in this paper are shown in the second, third, fourth and fifth columns in Figure 2 respectively. According to the diagram, the results of the ICM algorithm are the worst. It only takes into account the spatial interaction between pixels on a single scale and does not accurately describe the features of the textures. Obviously, the fifth column is better than the third column. The corresponding segmentation results have good regional consistency, and there is no obvious boundary deformation at the same time. Because modeling the spatial information on each scale by using RMRF can describe the characteristics of each texture more accurately. Meanwhile, it can avoid the mixture of texture boundaries. The results of the fifth column in Figure 2 are also significantly better than the results of the fourth column, which shows that the wavelet domain MsRMRF segmentation algorithm proposed in this paper can make full use of the regional interaction information on multi-scale, and has the ability to describe the nonstationarity of the image.

In order to compare the advantages and disadvantages of the segmentation results directly, the segmentation error rate is used to evaluate each segmentation result, and is recorded in Table 1. The segmentation error rate is defined as the ratio of the number of the mis-segmented pixels to the number of the pixels of the image, and the values are between 0~1. The closer to 0, the better the segmentation results are, and vice versa. It’s easy to see from table 1 that the average segmentation error rate of this algorithm is minimal (close to 0.015), which further proves the effectiveness of the algorithm proposed in this paper.

Table 1. Quantitative comparison of segmentation results (%)

	ICM     MRMRF    Literature [18]     MsRMRF
Figure 2(a1) Figure 2(b1) Figure 2(c1) Figure 2(d1) Mean	14.39          9.72               3.47             1.25 37.66         14.36              11.09             3.54 13.91           4.78                6.32              1.07 27.99          0.84               0.93             0.23 23.49          7.43               5.45             1.52

In order to further verify the segmentation performance of the algorithm, we use two remote sensing images, as shown in Figure 3, to carry out a segmentation experiment. (a1) in Figure 3 is a QuickBird remote sensing image. It can be clearly seen from the image that mainly three types of ground objects are included: forest, built-up area and farmland. So the corresponding classification number is 3. (b1) in Figure 3 is a remote sensing image of Spot5. There are four main types of ground objects in the image: built-up area, woodland and two different types of farmland. Therefore, the corresponding classification number is 4. As there is no real object as reference, we only make a qualitative evaluation on the segmentation results of these two remote sensing images. Firstly, the mixed segmentation between different ground object types is serious in the segmentation results of ICM algorithm, and the regional consistency is poor. Secondly, although the MRMRF segmentation algorithm can obtain better regional segmentation results, the mixed segmentation is still serious, and the boundary of the region is deformed obviously. Besides, in the segmentation results of literature [18], the mixed segmentation has been reduced, but the classification error is still more significant. The segmentation results of the algorithm proposed in this paper are obviously superior to the reference algorithm both in regional consistency and boundary smoothness, which further proves that the use of the wavelet regionlevel MsRMRF can better model the texture information and obtain more accurate segmentation results.

(a1)

(b1)

(b5)

(a5)

Fig. 3. The segmentation results of remote sensing image: The first column is the original images, the second column is the segmentation results of ICM, the third column is the segmentation results of MRMRF, the fourth column is the segmentation results of literature [18], and the fifth is column the segmentation results of MsRMRF

• 5.    Conclusion

This paper proposes an image segmentation algorithm based on multi-scale region MRF model in wavelet domain. The algorithm can take into account the wavelet information and regional interaction information at different scales and can take into account the wide range of spatial information. Meanwhile, it makes up for the deficiency of single scale MRF model in describing image non-stationarity. Therefore, it is able to describe the characteristics of different textures more accurately. The segmentation experiment of synthetic texture image and remote sensing image shows that this algorithm can obtain more accurate segmentation results.