Упорядоченная форма квадратичного экспоненциала в алгебре Гейзенберга-Вейля

Чтобы читатель сразу понял тематику предлагаемой статьи и используемые в ней технические приемы, начнем, вопреки обыкновению, с двух известных результатов, получивших свое отражение даже в монографической литературе. Оба. эти результата, оказываются частными случаями доказанной в п. 60 теоремы и иллюстрируют ее возможности.

2.    Процесс Орнстейна—Уленбека

Первый из этих результатов связан с теорией вероятностей.

В своем замечательном учебнике [1] Феллер, выписав обратное уравнение Колмогорова.

дu(t,ж)    1 d2u(t, ж)      дu(t,ж)

dt 2 дж2     рж дж для случайного процесса. Орнстейна—Уленбека, описывающего движение броуновской частицы при воздействии упругой силы, рекомендует сначала произвести в уравнении (1) замену функции

и(1,ж)= u(t,x exp(pt)), (2)

а затем ввести «новое время»:

1 — exp(— 2pt) 2p

В результате этих операций уравнение (1) превращается в стандартное уравнение диффузии, откуда, становится очевидным тот факт, что плотности переходных вероятностей рассматриваемого процесса являются гауссовскими со средним значением ж exp(—pt) и дисперсией т. задаваемой (3).

Разумеется, совсем нетрудно провести предлагаемые выкладки и убедиться в правильности приведенных рекомендаций. Однако, почему именно необходимо производить указанные замены, в учебнике никак не объясняется, что не может не вызвать у критически настроенного читателя чувства, некоторого неудовлетворения.

Покажем, что рекомендуемые Феллером преобразования вытекают из следующих алгебраических соображений. Довольно понятно, что решение u(t, ж) задачи Коши для уравнения (1), удовлетворяющее начальному условию и(0,ж) = /(ж), может быть записано в виде

u(t,ж) = exp{t(D²/2 — pжD)}[f (ж)], (4)

где символом D = d/dж ('здесь и далее) обозначен оператор дифференцирования по ж. а сам символ ж понимается как оператор умножения на ж. Однако, как это легко выводится из доказанного в п. 60 результата, экспоненциальный оператор в (4) допускает следующую факторизацию:

exp{t(D2/2 — pxD)} = exp{—tpxD)} exp{TD2/2},

где т задается соотношением (3).

Экспоненциальные сомножители в (5), как нетрудно в этом убедиться, представляют собой операторы, действующие согласно соотношениям (заметим, что т >  0)

exp{—tpxD)}[/ (x)] = / (x exp(—pt)),                           (6)

и

exp{T (D2/2}[/(x)]

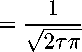
Z~ J ^y2 1

^exp [2Tp^{(x + y)dy}.

3. Гармонический осциллятор

Второй иллюстративный пример связан с квантовой механикой.

В монографии [2] (Теорема 12.63) приводятся пять различных доказательств следующего утверждения.

Теорема. Оператор exp{— tH}, где Н = —D² + x² — 1 - гамильтониан гармонического осциллятора, является ядерным интегральным оператором, ядро которого имеет вид

Qt

где

^Ft^(x.y) = 1 -_exp(_—4t) [|^{(1 — ex}p^(—4t))(x2 + y^{2) — 2x}y^exp^(—2t)j .          (9)

Приведенный результат опять-таки является следствием доказываемой в настоящей работе теоремы, из которой в качестве частного случая вытекает следующее факторизаци-онное тождество:

exp{t(D2 — x2)} = (cosh2t) 1/2 exp [—x~ tanh2t] x

(Ю)

x exp [—xD In cosh 2t] exp

Г D2

tanh 2t

Это тождество вместе с соотношениями (6) и (7) позволяет утверждать, что

exp [t(D2 — x2)]

[/(x)] = (cosh2t)-1/2 exp [— yS| E/ (+Ч-) -

где к = tanh2t, р_к обозначена случайная величина, имеющая нормальное распределение с нулевым средним и дисперсией к, а Е - знак математического ожидания. Это равенство позволяет представить соотношения (8) и (9) приведенной теоремы в более экономном виде, а именно:

exp{—tH}[/(x)] = exp(t)(cosh2t) 1/2 exp

— -к Е/ (—- + p_KA .

2        \ cosh 2t     /

(И)

• 4.    Алгебра Гейзенберга—Вейля

• 5.    Квадратичный экспоненциал

Часто алгеброй Гейзенберга—Вейля [3], а иногда просто алгеброй Вейля, называют кольцо дифференциальных операторов с полиномиальными коэффициентами над фиксированным полем (с нулевой, как правило, характеристикой). Нам удобнее определить этот объект более абстрактно как фактор-алгебру свободной алгебры (над произвольным полем) с тремя образующими а, b и с по идеалу, порожденному тождествами

[a, b] = ab — ba = с, [a, с] = [b, с] = 0.                              (12)

Эти равенства в квантовой физике называют каноническими коммутационными соотношениями. Именно таким коммутационным соотношениям подчиняются как бозонные операторы рождения и уничтожения, так и операторы положения и момента в квантовой механике [2].

Обозначим

Н = aa² + Pab + ^ba + 5b²,                          (13)

где а, 3,7,5 — заданные постоянные, а символы a, b и с подчиняются соотношениям (12). Формальный степенной ряд по формальной переменной t вида д = g(t;a, 3,7,5) = exp(tH),                              (14)

где Н задается (13), будем называть квадратичным экспоненциалом в алгебре Гейзенберга—Вейля. Наша основная цель — найти удобное для использования разложение функции g(t; а, 3,7, 5) переменных a, b, с, подчиняющихся соотношениям (12), на «простые» множители.

• 6.    Факторизация

Нас будет интересовать представление д в виде exp(tH) = exp(^a2) exp(gab) exp(^ba) exp(Өb2) = е1е2езе4,(15)

где ^,g,C и Ө искомые функции аргументов а, 3,7,5, с и t. Чтобы найти эти функции, продифференцируем соотношение (15) по t, снося при этом показатели соответствующих экспонент вправо от них. Это приводит к равенству exp(tH )Н = ^e1a2e2e3 е4 + д' e1e2abe3e4 + С, ' e1e2e3bae4 + Ө' е1е2езе4Ь2.(16)

Удобно переписать соотношение (16) с учетом равенства (15) в виде

Н = £ 'е-1 e-1e-1a2e2e3e4 + g'e-1e-1abe3e4 + ('e^bc^ + Ө'Ь2.(17)

Правую часть равенства (17) можно легко преобразовать, последовательно используя следующие соотношения:

exp(—Tba)a2 exp(Tba) = a2 exp(2тс);

exp(—Tab)a2 exp(Tab) = a2 exp(2тс);

exp(—Tb2)ba exp(Tb2) = ba + 2тсЬ2;(20)

exp(—Tb2)ab exp(Tb2) = ab + 2тсЬ2;(21)

ехр(—тЬ²)а² ехр(тЬ²) = а² + 2тс(аЬ + Ьа) + 4т²с²Ь².

Установим справедливость лишь наиболее сложного равенства (22), поскольку все остальные соотношения доказываются аналогично (только короче). Обозначим временно символом у выраокопие ехр( —тЬ2)а? ехр(тЬ2). Диффщюшщруя у по т. находим, что у' = ехр(—тЬ2)[а2, Ь2] ехр(тЬ2).

Заметим теперь, что из коммутационных соотношений (12) следует равенство [а2, Ь2] = 2с(аЬ + Ьа).

Поэтому использование (20) и (21) приводит к следующей задаче Коши: у' = 2с(аЬ + Ьа + 4тсЬ2), у|т=о = а2, решение которой задается (22). Если с использованием (18) — (22) преобразовать тождество (17), сравнить коэффициенты при а2,аЬ,Ьа и Ь2 и разрешить полученные равенства относительно У, У, С',Ө', то в результате приходим к следующей системе дифференциальных уравнений:

£' = а ехр(—2с(у + ());

У = 3 — 2саӨ;

У = у — 2саӨ;

Ө' = 5 — 2с(3 + у )Ө + 4ас²Ө².

Отметим сразу же, что, как нетрудно убедиться непосредственной проверкой, решение Ө последнего уравнения в (23) имеет вид

Ө 5          sinh ty

y cosh ty + с(3 + у) sinh ty¹

где

y = с V (3 + у )² — 4а5.

Из (23) видно, что остальные искомые функции £,у и £ находятся с помощью последовательного интегрирования правых частей оставшихся уравнений.

Оказывается, что можно найти функции £, у и £ и без использования операции интегрирования. В самом деле, если повторить описанную выше процедуру, приведшую к системе дифференциальных уравнений (23), с той разницей, что при дифференцировании (15) по t сносить показатели соответствующих экспонент влево (а не вправо, как это было) от них, то в результате придем к системе дифференциальных уравнений:

Д = а — 2с(3 + у )£ + 45с²32;

У = 3 — 2с5Д

У = у — 2с5е;

Ө' = 5 ехр(—2с(у + С)).

Сравнение вторых (или третьих) уравнений в (23) и (26) приводит к равенству

5^ = аӨ,

и поэтому

„               sinh ty

^ = а------------у-—7-----, y cosh ty + с(3 + у) sinh ty

где ц задается (25).

Вычитая средние равенства системы (23) (или (26)) одно из другого, убеждаемся, что

7 ^-С = ^{(3 -} 7^)і.

Наконец, соотношения (27) и (25) вместе с равенством а — 2с(3 + 7)£ + 4с25£2 = a exp(—2с(7 + С)),

получаемым приравниванием правых частей первых уравнений в (23) и (26), дают возможность показать, что cosh іц +—7^ sinh іц ц

7 + С = с ln f

Полусумма и полуразность правых частей (28) и(29) определяют искомые функции 7 и С, соответственно.

Подводя итог приведенным рассуждениям, можно утверждать, что справедлива следующая

Теорема. Пусть

Н = aa2 + 3 ab + 7ba + 5b2, где а, 3,7,5 — заданные постоянные, а символы a,b и с подчиняются коммутационным соотношениям

[a, b] = ab — ba = с, [а, с] = [b, с] = 0.

Тогда для формального степенного ряда exp(tH) (по формальной переменной t) справедливо факторизационное тождество exp(tH) = exp(£a2) exp(^ab) exp(Cba) exp(Өb2),

где

£ = a

sinh іц ц cosh іц + с(3 + 7) sinh іц

7 =

^{3 —} 7

^{t +} 2с

ln

cosh іц +

с(3 + 7)

--------- sinh іц , ц

С =

7 - ³

^{і +} 2с

ln

cosh іц +

с(3 + 7)

--------sinh іц ц

Ө = 5

sinh іц ц cosh іц + с(3 + 7) sinh іц

и ц = с V (3 + 7 )2 — 4а5.

7.    Процесс Орнстейна—Уленбека

Чтобы убедиться, что соотношение (5) является простым следствием доказанной теоремы, следует прежде всего заметить, что коммутатором оператора дифференцирования D = d/dx II оператора х умножения на аргумент яв.тшлея тождествепный оператор 1. Поэтому, полагая в теореме a = x,b = D,с = —1 и выбирая параметры квадратичного экспоненциала а = 0,3 = —Р,7 = 0 и 5 = 1/2, после несложных подсчетов находим, что £ = 0,7 = —pt, С = 0 и Ө = т, где т задается соотношением (3), что и приводит к равенству (5). Стоит отметить, что равенства (6) и (7) наряду с (5) позволяют записать решение (4) в виде

n(t,x)=E/(7_Т + х exp(—pt)),                            (30)

где 7t ~ стандартпын винеровский процесс. Е — знак математического ожидания, а т задается соотношением (3).

Представляет также интерес двойственное к (5) представление exp{t(D2/2 — pxD)} = exp{AD2/2} exp{ —tpxD)}, где

exp(2pt) — 1

А = --------- 2p

Этот резулвтат также является следствием доказанной теоремы, посколвку если в ней выбрать а = D, b = x, c = 1. то моментально обшаружтпзается. что £ = А, p = 0, £ = —pt и Ө = 0, поэтому имеет место (31) и (32). Приведенные соображения позволяют представить решение (4) в двойственной по отношению к (30) форме:

n(t, x) = Е/((pA + x) exp(—pt)), где по-прежнему pt ~ стандартный винеровский процесс, Е — знак математического ожидания, а А задается соотношением (32).

8.    Гармонический осциллятор

Покажем, что факторизационное тождество (10) является следствием доказанного нами утверждения. В самом деле, как и в п. 7, полагаем в теореме а = x, b = D, c = —1 и выбираем параметры квадратичного экспоненциала а = — 1,3 = у = 0 и 8 = 1. Легло убедиться, что при таком выборе параметров получаем £ = — 2 tanh2t, p = £ = — 2 lncosh2t и Ө = 2 tanh2t. Следовательно, имеет место представление exp{t(D2 — x2)} = exp

x²       xD

—к   exp —— In coth 2t

x exp [—Dx In cosh 2t] exp

[4 ],

где к = tanh2t. Если в третьем сомножителе равенства. (33) заменить оператор Dx равным ему оператором 1 + xD, то придем с соотношению (10).

Отметим также двойственное к (33) равенство exp{t(D2 — x2)} = exp

D2 Dx к exp     In coth 2t

x exp [xD In cosh 2t] exp

һт ] -

которое получается, если в факторизационной теореме положить а = D, b = x и, следовательно, c = 1. Соотношение (34) в свою очередь приводит к альтернативному представлению ядра, оператора, рассматриваемого в теореме и. 3.

9.    Упорядоченность

Доказанное в п. 6 факторизационное тождество может быть представлено в несколько иной форме, более приспособленной для решения некоторых задач, возникающих в квантовой физике. Заметим прежде всего, что, в силу коммутационных соотношений (12), exp{pab} exp{£ba} = exp{(p + £ )ab} exp{—c£}.

Покажем теперь, что для формального степенного ряда exp{tab} справедливо представ ление

ex

~ а^ Г1 ^:p{tab} = Е Т!

=

—

п=0

exp{—ct} ]n

В самом деле, если искать упорядоченное представление экспоненты, стоящей слева в равенстве (36) в виде

∞

E^{a b} г

—j- [u] , n=0

где p — искомый степенной ряд по формальной переменной t, то дифференцирование этого соотношения по t приводит к равенству ab exp{tab} = pa exp{tab}b.

Остается лишь заметить, что из коммутационных соотношений (12) вытекает равенство exp{rtab}b exp{ — rab} = b exp{ct}.

Следовательно, p' = exp{—ct}, что и доказывает (36).

Удобно представление (36) записывать в виде exp{ta4 = exp (a^ [1 — exp{-=t} П ,

где символы а2 и bi считаются коммутирующими, в любом мономе результирующего выражения символ a2 ставится левее символа bi, и после этого индексы удаляются. Придерживаясь этого соглашения и используя равенство (29), убеждаемся, что exp{(r + С)ab} = exp {a2bi [^(c^-) 1j } ,

где

sinh tu

.

r(t) = coth tp + c(P + у)------ U

Кроме того, ясно, что exp{—c(} = r(t)-i/2exp ^-^ct} .

Приведенные соображения позволяют переформулировать теорему и. 6 в следующем виде.

Теорема. Пусть

Н = аа? + Pab + yba + 5b2, где а,Р,у,5 — заданные постоянные, а символы a,b и c подчиняются коммутационным соотношениям

[a, b] = ab — ba = c, [a, c] = [b, c] = 0.

Тогда для формального степенного ряда exp(tH) (по формальной переменной t) справедливо тождество exp(tH) = r(t) 1/2 exp ha2 + a^bir(t) - + 9b2 + (P y)ct 1, cr(t)                   2

где

sinh tu

(= айд - sinh tp 9 =          , и введены обозначения p = c р (P + у )2 — 4а5, r(t) = coth tp + c(p + у )snh-tu. U

Символы с индексами (т.е. a2 и bi) в правой части приведенного равенства считаются коммутирующими и предполагается, что в любом мономе результирующего выражения символ bi ставится правее символа a2, после чего индексы удаляются.

10.    Сжимающий оператор

Ограничимся лишь одним примером, иллюстрирующим сформулированное утверждение.

Концепция сжатых состояний возникла в квантовой оптике еще в семидесятых годах прошлого века [4] и оказалась весьма полезной в различных разделах квантовой физики (см., например, обзор [5]). Сжимающим оператором называют оператор

S = exp{iX(QP — г/2)},

где Q и P — связанные с гармоническим осциллятором операторы положения и момента соответственно и X — параметр, характеризующий сжатие. Эти операторы удовлетворяют коммутационному соотношению:

[P,Q]= г.

Если выразить оператор S в терминах бозонных операторов рождения А^ и уничтожения А. учитывая, что

Q = 2-1/2(А| +А),     P = г2-1/2(А^ — А), то (39) примет вид

^S = exp ^X^A^{2 —} Д^} .

Поскольку бозонные операторы А и А^ подчиняются коммутационному соотношению

[А, А1] = 1, где 1 означает тождественный оператор, сформулированное в предыдущем пункте утверждение после простых подсчетов приводит к равенству

S = (cothX)-1/2 : exp 1 — ^А² + ¹ " =°^thXАА + ^А²! : .

2           cothX            2

Здесь символ : . : означает нормальную упорядоченность соответствующего выражения, при которой сначала действует оператор уничтожения А и лишь затем оператор рождения А*.

Если символом :.: обозначить антинормальную упорядоченность, когда в любом мономе оператор рождения стоит правее оператора уничтожения, то, как легко убедиться, из теоремы и. 8 вытекает представление tanh X     coth X — 1       tanh X s = (cothX)-1/2 exp{—А2 +   _ АА* - —А'  .