Управление автономным подводным аппаратом хорошо обтекаемой нецилиндрической формы

Автономные подводные аппараты играют огромную роль в проведении современных исследований в самых разных областях знаний, таких как океанология, экология, климатология и многих других. Кроме того, без подводных аппаратов невозможно представить проведение картографических, поисковых, мониторинговых работ. Особенно востребованными являются необитаемые подводные автономные аппараты, которые не требуют присутствия оператора и способны добраться туда, куда человек попасть не может. Перед подобными аппаратами постоянно ставятся новые цели, что требует разработки новых и улучшения существующих методов создания автоматических систем управле- ния. Общие принципы управления подвижными объектами и формирования математических моделей представлены в [15]. Данная статья посвящена формированию автоматического управления для необитаемого аппарата хорошо обтекаемой нецилиндрической формы, представленного на рисунке 1.

Аппарат имеет сплюснутую форму и два тоннельных гребных винта. Подводные аппараты такой формы являются наиболее универсальными, поскольку их форма позволяет достаточно легко навешивать на них разнообразное дополнительное оборудование прямо на месте перед спуском в воду.

Рис. 1. Необитаемый автономный подводный аппарат

Нелинейная математическая модель движения подводного аппарата в горизонтальной плоскости имеет вид [6, 7]:

m

u -

vr + wq - Xg lq + r

2)+ yG(pq - r)+zg (pr+q) = X,

m

v + ur - wp +

xg (pq + r)- yG(p2 + r2)+ zg (qr- p) = Y,

mw - uq + vp + Xg (pr - q) + yG (qr + p) - zg

(p2 + q2

)]=Z.

После линеаризации и перехода от системы обозначения SNAME к обозначениям, принятых в российских исследованиях, получаем следующую математическую модель:

V z = a_nV_z + a^ y + b i S + F,

® y = ^a21^Vz ^{+ a}22 ^ y + ^b2 ^{S +} M,

S = u,y = ф.

ствие; y - выход системы; F и M -внешние силы и моменты.

Рассмотрим математическую модель закона управления, который гарантирует определенную величину угла курса ф _z :

Здесь Vz и My - проекции линейной и угловой скоростей соответственно на оси Oz и Oy системы координат, начало которой расположено в центре масс подводного аппарата; ф - угол курса; S - угол отклонения рулей; u - управляющее воздей- z 1 = a11z1 + a12z2 + b1Sr + g1(ф - z3), z2 = a21z1 + a22z2 + b2Sr + g2(ф - z3),

z3 = z2 + gз(ф - z3),u = P1z 1 + P2z2 + P3z3 + ^(ф - Фz )+ X.

Система уравнений, определяющая фильтрующий элемент % :

/ p = ap + ^(ф - z3 ),

X = p2,где p = ( pi p2 Рз )T.

Коэффициенты gi при этом обеспечивают биномиальное распределение корней характеристического полинома асимптотического наблюдателя с заданным пара- метром Ро = 0.6. Коэффициенты Pj являются коэффициентами скоростного закона управления.

Для скорости хода V = 1.5 м/с здесь коэффициентов: приняты следующие значения постоянных

ап = -0.3321, a12 = 1.6444, b1 = 0.1186;

a21 = 0.0633, a22 =-0.5015, b2 = 0.1141.

Отметим, что указанные коэффициенты скоростных законов получены путем решения соответствующей задачи LQR- u = -0.1828 Vz -1.5545 av - 0.6324

zy

Рассмотрим в качестве заданного движения поворот по курсу на заданный угол pz = 10 ° . На рисунке 2 и 3 представлены графики отклонения рулей и курса в процессе стабилизации аппарата при его движении в повороте по курсовому углу для скорости хода V = 1.5 м/с в линеаризованной модели, а на рисунке 4 и 5 – в не- оптимизации. Ее решение в виде управления по состоянию имеет следующий вид:

p - 0.6310 s r .

линейной модели. Этот процесс обеспечивается приведенными выше законами управления. На рисунке 4 проиллюстрированы перекладки вертикальных рулей. Рисунок 5 показывает график изменения курса p (t) с его выходом на заданный уровень.

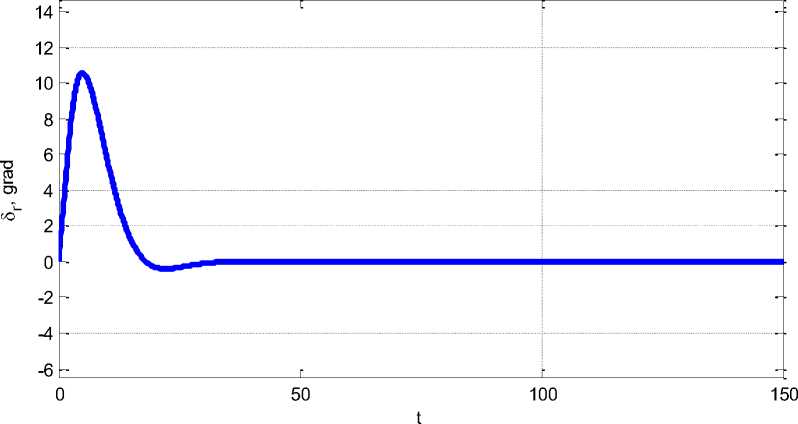
Рис. 2. Отклонение рулей в линейной модели

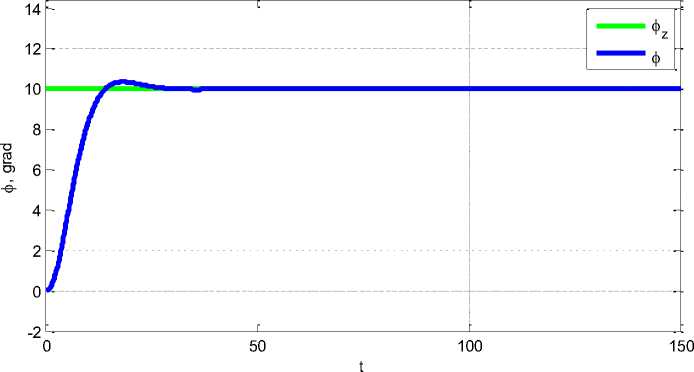
Рис. 3. Изменение курса в линейной модели

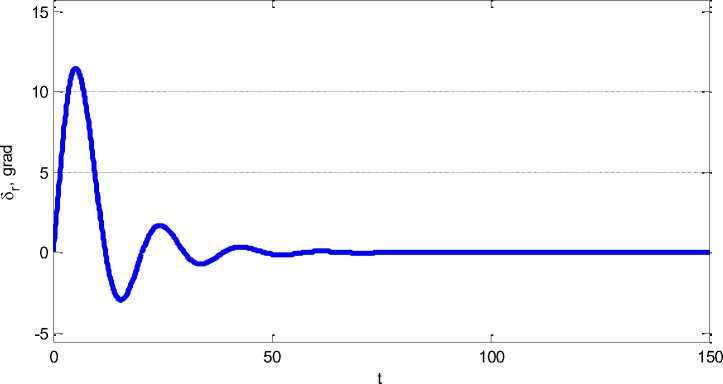
Рис. 4. Отклонение рулей в нелинейной модели

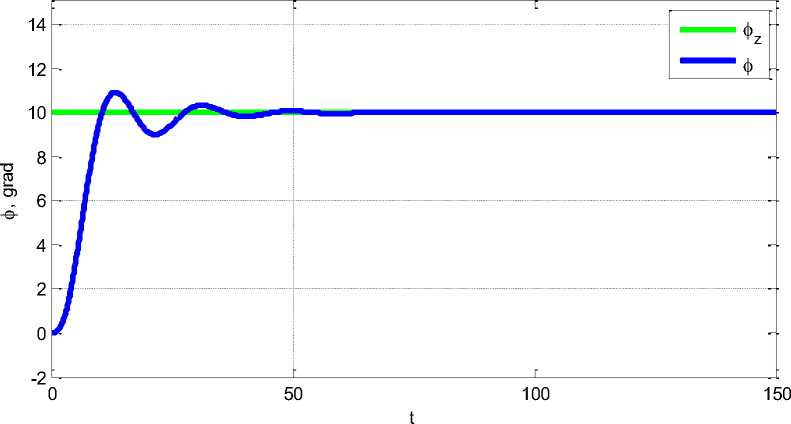
Рис. 5. Изменение курса в нелинейной модели

Из приведенных графиков видно, что на 42-й секунде угловая координата выходит на заданное значение p z = 10 ° и находится в этом положении. При этом управление, сформированное для линейной математической модели, хорошо работает и для нелинейной математической модели.

Таким образом, в данной статье представлена система автоматического управления в горизонтальной плоскости для необитаемого автономного подводного аппарата хорошо обтекаемой нецилиндрической формы. Тестирование сформированной системы управления для линейной и нелинейной математических моделей проведено в среде MATLAB.