Управление безопасностью объекта техносферы на основе закона сохранения целостности объекта

Управление безопасностью объекта техносферы представляет собой сложную комплексную задачу. Любая авария подобного объекта несет за собой определенные угрозы для безопасности человека. Подобные угрозы бывают прямыми, влияющими на здоровье человека. Данные угрозы образуются в связи с формированием негативных факторов после аварий на объекте техносферы, таких как пожа- ры, радиационное заражение и т.п. Также, авария на таком объекте приводит к утрате объектом своего предназначения, что влечет за собой экономические и социальные проблемы. В рамках данной статьи, понятие безопасности объекта техносферы трактуется, как способность объекта выполнить свое предназначение в постоянно изменяющихся условиях. [1]

Данная работа представляет собой инновационный подход к проблеме управления безопасностью объекта техносферы. В настоящее время, безопасность обеспечивается подходом на основе анализа. Этот подход построен на оценке произошедших аварий, сравнении различных объектов и прогнозировании возможных проблем в процессе существования объекта. В отличии, от существующего подхода, метод описанный в данной статье позволяет создавать процесс с заранее установленным показателем безопасности объекта.

Основой управления безопасностью является решение. Создание модели решения это задача лица принимающего решения (ЛПР). Данная модель обязана учитывать базовую закономерность предметной области. Подобной базовой закономерностью является закон сохранения целостности. Для обоснования необходимости выявления условия существования процесса, необходимо применить формальный аксиоматический метод. [2,3]

Закон сохранения целостности объекта (ЗСЦО) – устойчивая повторяющаяся связь свойств объекта и свойств действия при фиксированном предназначении. ЗСЦО проявляется во взаимной трансформации свойств объекта и свойств его действия при фиксированном предназначении. ЛПР, как и любой человек познает и осознает Мир через три базовых свойства Мира – «объективность», «целостность» и «из-менчивость».[4] В соответствии с ЗСЦО каждый процесс должен быть представлен тремя взаимосвязанными компонентами в виде процесса - «объект», «предназначение» и «действие». Эти три компонента располагаются по горизонтали. Также, правильно построенная теория должна иметь три уровня (рис. 1): [2,3]

• 1.    Методологический уровень – определение условий существования процесса управления;

• 2.    Методический уровень – разработка метода, позволяющего обеспечить условия перевода объекта управления из настоящего состояния, в требуемое;

• 3.    Технологический уровень – получение условий реализации процесса перевода объекта управления из настоящего состояния, в требуемое.

При развертывании понятия «Управленческое решение» от практики, необходимо рассмотреть три следующих метода познания (рис. 2): [2,3]

• -    Декомпозиция - научный метод, использующий структуру задачи и позволяющий заменить решение одной большой задачи ре-

• шением серии меньших задач, пусть и взаимосвязанных, но более простых

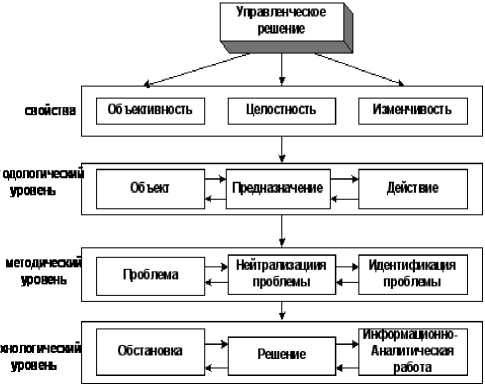
Рисунок 1 – Развертывание понятие «Управленческое решение» от теории

• -    Абстракция (математическая интерпретация) – мысленное отвлечение, обособление от тех или иных сторон, свойств или связей предметов и явлений для выделения существенных их признаков

• -    Агрегирование – процесс объединения элементов в одну систему

Управленческое решение

Декомпозиция

ИнформационноАналитическая

1 Нейтрализация <

1 проблемы

Абстрагирование

р F(A/nn, А/нп ,А/ИП.)

Агрегирование

Рисунок 2 – Развертывание понятия «Управленческое решение» от практики

Таким образом, управленческое решение есть обеспечение субъектом условий реализации предназначения объекта, которым он управляет, в соответствующей обстановке. Обстановка – совокупность факторов и условий, в которых осуществляется деятельность. [2,3]

Из системотехники известно, что возможны два подхода к построению систем – анализ и синтез.[4] При анализном подходе

(решении проблемы выбора) есть набор физических элементов (исходных данных) по которым можно прогнозировать возможный результат деятельности системы. Данный подход имеет существенный недостаток – он не позволяет формировать процессы с заранее заданными свойствами, что особенно необходимо в условиях деятельности аналитической развед-ки.[5] Синтезный подход лишен данного недостатка, так как он моделирует систему в зависимости от конечных характеристик, что позволяет достигнуть заданной цели. [1,6]

• •    Проблемы возникают с частотой зависящей от Δt ПП – среднее время возникновения опасности (проявления проблемы) (рис. 3а)

• •    Для нейтрализации опасности, сотрудник должен быть способен определить ее. Идентификация зависит от Δt ИП – среднее время идентификации опасности (проблемы) (рис. 3b)

• •    После идентификации, сотруднику необходимо принять меры по нейтрализации опасности. Нейтрализация происходит с частотой зависящей от Δt НП (рис. 3с)

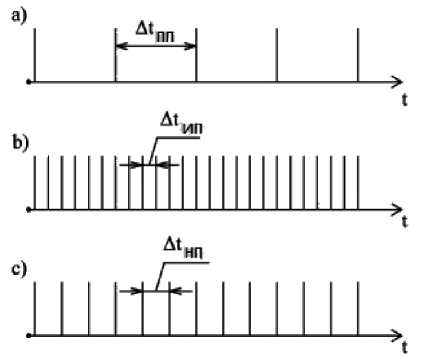
Рисунок 3 - Диаграмма проявления базовых элементов формирования управленческого реше-ния: а) время проявления проблемы; b) время идентификации проблемы; с) время нейтрализации проблемы.

Управление является эффективным, если соблюдается следующее уравнение

• ^А    t ИП ^{+ А} t НП < ^А t ПП . ⁽¹⁾

Исходя из данного уравнения заметно, что время на появление следующей проблемы должно быть больше чем время на идентификацию и нейтрализацию существующей.

Согласно гносеологическому представлению закона сохранения целостности объекта (рис.4), алгоритмами (технологиями) будут являться основные алгоритмы создания сетевой модели. Методами будут являться уравнения описывающие процессы(2-4), а методо- логией будет являться математическая модель управленческого решения (5). [1,6]

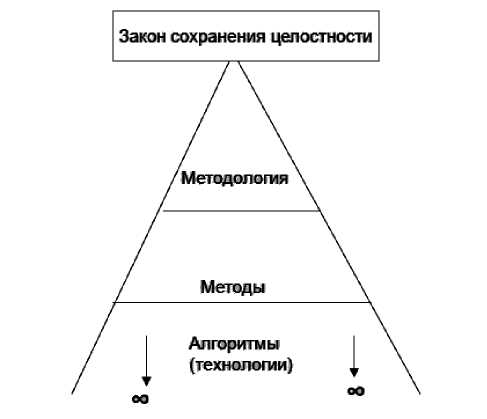
Рисунок 4 - Схема гносеологического представления закона сохранения целостности объекта

При создании модели управленческого решения, рассматриваются три основных процесса:

• -    Процесс образования проблемы для системы аналитической разведки характеризуется ^*

вектором x

А t ПП = f1( x 1’ x 2’-’ xn ) .

• -    Процесс идентификации про-

• ^^

блемы характеризуется вектором y

А t ИП = f 2( У 1’ У 2’-’ Уп ) .

• -    Процесс нейтрализации пробле

мы характеризуется вектором z

А t YП = f 3 (z 1 ’ z 2 ’"’’ zn ) .

Математическая модель управленческого решения принимает вид (5)

P = ( А t ПП ’ А t ИП ’ А t НП )

В данных соотношениях обстановке соответствует характеристика периодичности проявления проблемы в информационной системе Δt ПП , информационно-аналитической работе – периодичность идентификации проблемы в информационной системе Δt ИП , а предназначению – периодичность нейтрализации проблемы Δt НП .

Базовая модель управленческого решения имеет три основных элемента, что показано на рисунке 5. [7]

При трудовой деятельности возникают проблемы со следующей интенсивностью

X = ----

^А t ПП

.

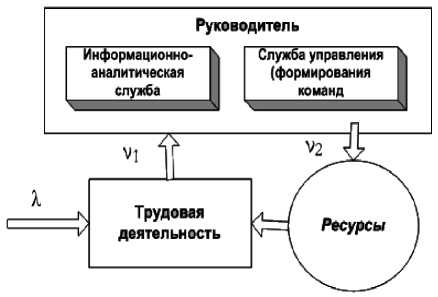
Рисунок 5 – Структурная схема реализации управленческого решения

Данные проблемы идентифицируются информационно-аналитической службой, интенсивность идентификации будет следующей

1 , x

^U 1

.

^ t ИП

Процесс по нейтрализации проблемы будет характеризоваться интенсивностью

^U 2

.

^ t НП

ЛПР может выполнять, в различных сочетаниях, две функции:[2,3,7]

-

-

Идентификация;

Нейтрализация.

Поэтому решение ЛПР имеет четыре базовых состояния:

• -    А 00 – ЛПР не идентифицирует и не нейтрализует;

• -    А 10 – ЛПР идентифицирует и не нейтрализует;

  - А 01

  
  

  ЛПР не идентифицирует но

  
  

  _–

  
  

нейтрализует;

• -    А 11 – ЛПР идентифицирует и нейтрализует.

В соответствии с такой особенностью управленческого решения необходимо ввести вероятности P 00 , P 10 , P 01 , P 11 нахождения нашей системы управления в этих четырех состояниях. [8] Используя данные состояния системы, возможно составить граф состояний процесса формирования управленческого решения (рис.6).

Согласно данному графу возможно определить два основных пути развития ситуации.

Первый путь возможен, когда если проблема нейтрализована, а новая не образовалась

A       U1

^ 00 ^ ^ 10 ^ ^ 01 ^ ^ 00 .

Второй путь заключается в том, что проблемы образуются подряд

A      U1      A z     U2      U1     \A

• ^ 00 ^ ^10 ^ ^01 ^ (^11 ^^10 ^ ^01)^ ^

U1

^ Л 01 ^ Л 00 . ⁽¹⁰⁾

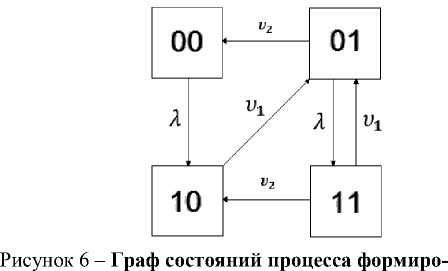
вания управленческого решения

Каждому из состояний А, соответствуют вероятности состоянии P i (t) , которые находятся путем решения системы дифференциальных уравнений (уравнений Колмогорова), имеющих вид, в котором i = 0, 1, ... , n. [9]

dP i ( t )

dt

n

n

= E ^A, ^Pj (t ) - P ( t ) E A ⁽¹¹⁾

j = 1

j = 1

Величина A ji P j (t) называется потоком вероятности перехода из состояния S i в состояние S j , причем интенсивность потоков 2 jj может зависеть от времени или быть постоянной. [10]

Таким образом, система ДУ Колмогорова для нашей ситуации будет иметь следующий вид (12).

f d

I ^P 00 ⁽ t ) =

_I dt

d j —P 01 (t) =

^I dt

d

- P 00 ( t ) ^A + P 01 ( t ) U 2

- P 01 ( t )( A + и 2 ) + P 11 ( t ) u 1 + P 10 ( t ) u 1

I       P 10 ( t ) = ^P 00 ( t ) ^A

I dt

I

I — P 11 ( t ) = P 01 ( t ) A

L dt

^{- P} 10 ⁽ t ^{) u} 1 ^{+ P} 11 ⁽ t ^{) u} ₂

^{- P} 11 ⁽ t ^{)( U} 1 ^{+ U} ₂)

Так как система имеет конечное число состояний А, то сумма вероятностей нахождения системы в любом состоянии равно единице

P ₀₀( t ) + P _w( t ) + P 01 ( t ) + P 11 ( t ) = 1 .   (13)

Если предположить, что мы имеем стационарный процесс, тогда наша исходная система дифференциальных уравнений трансформируется в систему линейных однородных уравнений следующего вида (14):

f- P00 (t)A + P01 (t)U 2

J- P 01 (t)( A + U 2) + P11 (t )u 1 + P10 (t )u 1 = 0

I ^P 00 ( t ) ^A \ P 01 ( t ) A

P10 (t )U 1 + P11 (t )U 2

^P 11 ⁽ t ⁾⁽ U 1 + V J = ⁰

Решением данной линейной алгебраической системы уравнений являются следующие соотношения (15):

I P 00

P ¹⁰

^

p

I 01

^U 1 ^U 2

X ( X + u_x + и_г ) + и_хи_г

Xu ₂( X + u + и_г )

( u 1 + u 2 )[ X ( X + u + u 2 ) + u^ 2 ] (15)

Xu

X ( X + v, + u ₂) + u,u₂

Xu !

^{( U} 1 ^{+ u} 2 ^{)[ X ( X + u} i ^{+ u} 2 ) ^{+ u} i ^u 2^]

Основное уравнение показывает веро- ятность нахождения системы в момент состояния, когда существовавшая проблема решена, а новая еще не наступила (16). Данный показатель является критерием безопасности. [2,3,11]

^u 1 ^u 2

P 00

. (16)

X ( X + u_x + u ₂ ) + u_iu₂

Для решения обратной задачи, необходимо определить следующие интенсивности:

1. блемы

2. проблемы

3. проблемы

интенсивность проявления про-

X =------- ;

^A t ПП

интенсивность идентификации u 1 =--------;

A t ИП интенсивность

нейтрализации

^u 2 = ----

.

^A t НП

Данная модель обеспечения ности объекта техносферы на законе ния целостности объекте учитывает безопас-сохране-условия

существования данного объекта. Использова- ние подхода на основе синтеза позволило сформировать модель управленческого решения, которое позволяет задать требуемый уровень безопасности. Подготовка кадров в области техносферной безопасности способных выработать адекватное решение в процессе управления является важнейшей задачей в существующих условиях развития человечества. [12]