Управление ближнепольной фокусировкой мезоразмерной бинарной фазовой пластинки в поле оптического излучения с круговой поляризацией

В связи с миниатюризацией элементов фотоники при стремлении увеличить разрешение фокусирующих устройств вплоть до субдифракционного, в последние годы отмечается повышение интереса к исследованию дифракционных оптических элементов в виде зонных пластинок Френеля (ЗП) с высокой числовой апертурой NA ~ 1. Такие дифракционные элементы фокусируют падающий свет вблизи своей теневой поверхности в области ближнего оптического поля, где, помимо уходящего излучения, присутствуют также и поверхностные затухающие (эванесцент-ные) волны. Конструктивная интерференция уходящих и эванесцентных волн может привести к формированию сингулярностей оптической фазы и возникновению так называемых суперосцилляций поля [1], что способно уменьшить диаметр фокусного пятна ниже дифракционного предела [2]. Преодоление ди- фракционного предела линз также актуально в оптической литографии [3], оптической микроманипуляции и оптических системах памяти [4, 5]. Отметим, что преодоление трёхмерного дифракционного предела становится возможным для дифракционных элементов, выполненных на криволинейной поверхности [6], однако практическая реализация таких фокусирующих схем усложнена.

Экспериментальные исследования фазовых зонных пластинок на подложке из плавленого кварца с различной числовой апертурой от 0,7 до 0,9, изготовленных с использованием литографии с электроннолучевым сканированием и технологии мокрого хромирования, были описаны в [7]. Для ЗП с числовой апертурой NA =0,7 на длине волны 400 нм измеренное разрешение составило около 300 нм. В [8] получено фокальное пятно шириной 0,33λ (λ – длина волны падающего излучения), а в работе [9] численно показана возможность фокусировки в фокальное пят- но диаметром 0,52λ с помощью простой фазовой ЗП. В [10, 11] численно и экспериментально было показано, что линейно-поляризованное излучение с длиной волны λ =633 нм может быть сфокусировано с помощью френелевской ЗП с субволновым фокусным расстоянием 0,5 мкм. Экспериментально наблюдалось эллиптическое фокусное пятно с наименьшей шириной 0,63λ. В [12, 13] теоретически и экспериментально впервые было показано, что для зонной пластины с высокой числовой апертурой и фокусным расстоянием, меньшим длины волны, достигается разрешение около трети длины волны для линейно-поляризованного излучения, при этом реальный и расчётный (геометрооптический) фокус не совпадают.

Необходимо отметить, что, когда свет фокусируется с помощью ЗП с высокой числовой апертурой, структура и симметрия фокального пятна существенно зависят от состояния поляризации падающей волны [14, 15, 16]. Например, остро сфокусированный пучок с линейной поляризацией создает эллиптическое фокусное пятно [12, 17], а использование радиально-поляризованного света позволяет получить фокальное пятно с размерами меньшими, чем при фокусировке линейно-поляризованного света [18].

Следует отметить, что, поскольку структура периферийной части зонной пластинки с коротким фокусом приближается к виду бинарного аксикона, особенности, указанные выше, справедливы и для акси-конов [19 – 21].

В то же время для ряда практических приложений бывает важно получить в фокальной плоскости осесимметричное распределение интенсивности поля, не зависящее от плоскости поляризации освещающей оптической волны. В этом случае целесообразно использовать излучение с круговой поляризацией, когда в формировании области фокусировки равноправно участвуют обе ортогональные компоненты поля. Но следует учитывать, что, исходя из принципа неопределённости Гейзенберга, можно утверждать, что пространственное разрешение ЗП, облучаемой излучением с круговой поляризацией, всегда ожидается хуже, чем в случае использования линейной или радиальной поляризации. Поэтому разработка методов получения высокого разрешения в случае круговой поляризации представляется актуальным.

Тенденция развития фокусирующих элементов микрофотоники в направлении плоскостной плёночной геометрии (2D-фотоника [22]), востребованных в разнообразных современных схемах оптической мик-рофлюидики и «лаборатория-на-чипе» устройствах [23, 24], выдвигает на первый план исследования по оптимальному конструктивному дизайну плоскостных линзовых метаструктур. Основные требования к таким зонным оптическим концентраторам – это максимально резкий и интенсивный фокус при минимально возможном вертикальном рельефе зон. По причине миниатюрных размеров для этих целей чаще всего используются бинарные зонные пластинки Френеля, которые выполняются в виде системы концентрических канавок прямоугольного сечения, вытравленных в тонкой диэлектрической или металлической плёнке [25, 26].

В настоящей работе представлены результаты численного моделирования бинарных фазовых френелевских ЗП мезоволнового размера и большим апертурным углом ( NA ~ 1) с целью оптимизации их фокусирующих характеристик. В процессе моделирования основное внимание было уделено изучению влияния глубины микрорельефа зон и толщины плёночной подложки на параметры фокуса ЗП. Как удалось установить, наиболее резкая фокусировка оптической волны вблизи ЗП достигается при глубине микрорельефа соседних френелевских зон, изменяющейся в диапазоне от четверти волны до полуволны внутри фазовой ступеньки. Для повышения пространственного разрешения области фокуса предложен оригинальный дизайн перевёрнутой фазовой ЗП с коническим иммерсионным слоем (ИЗП), что позволило реализовать фокусировку света в пятно с полушириной существенно ниже дифракционного предела.

Фокусировка излучения ЗП на базе диэлектрической пластинки

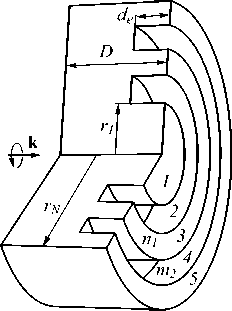
Рассмотрим следующую геометрию задачи (рис. 1 а ). Моделируемая фазовая зонная пластинка Френеля представляет собой диэлектрический цилиндр кругового сечения толщиной D , в котором нарезаны (вытравлены) концентрические канавки прямоугольного профиля глубиной d e . Диэлектрическая матрица считается непоглощающей в оптическом диапазоне волн, её показатель преломления обозначен как n 1 , а сама пластинка находится в воздухе с показателем преломления n 0 = 1. Со стороны подложки ЗП освещается циркулярно поляризованным излучением с плоским волновым фронтом с длиной волны X .

Радиусы зон пластинки Френеля r q вычисляются по известной формуле (см., например, [12, 27]):

r = ^f X + ( q X/ 2 ) ² , q = 1,2, ™ N , (1) что обеспечивает сдвиг фазы волны в п радиан на границах соседних зон. Здесь f d – расчётный фокус ЗП. Для определённости, в дальнейшем будем рассматривать ЗП с большой числовой апертурой NA = n 0 [1+( / d / r_N )²] ¹²~1, состоящей из пяти зон и с f_d = X , в поле монохроматической волны с X = 500 нм. Заметим, что ранее амплитудные и фазовые бинарные ЗП Френеля с фокусным расстоянием меньше длины волны излучения или равной использовались для повышения дифракционной эффективности субволновой фокусировки вплоть до X /3 [6, 12].

Электродинамическая задача о дифракции оптической волны на диэлектрической структуре моделировалась в рамках численного решения волнового уравнения для векторов поля в осесимметричной пространственной геометрии с помощью метода конечных элементов (FEM), реализованного в компьютерном пакете COMSOL Multiphysics (ver. 5.2a). Оптическая волна, освещающая микроструктуру, имела начальную амплитуду 1 В/м и распространялась в направлении волнового вектора k по нормали к плоскости ЗП. Сеточная дискретизация расчётной области производилась FEM-решателем автоматически при заданном максимальном размере треугольного сеточного элемента λ /(25 × n1). Как отмечено выше, ЗП располагалась в воздухе и окружалась системой идеально поглощающих цилиндрических слоёв (PML) для реализации условий свободного излучения на внешних границах расчётного домена.

б)

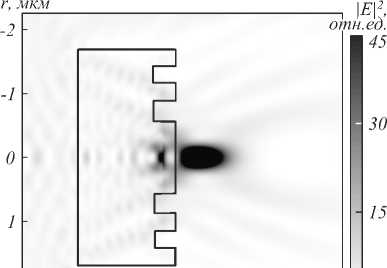
Рис. 1. COMSOL-модель пятизонной фазовой пластинки (пронумерованы красными цифрами) толщиной D, глубиной канавок d e , вырезанных в диэлектрике с показателем преломления n 1 (а); пространственный профиль интенсивности оптического поля |E|² при освещении кварцевой ЗП излучением с круговой поляризацией со стороны подложки (б)

Для примера на рис. 1 б показано двумерное пространственное распределение квадрата нормированного электрического поля | E |² (интенсивности) вблизи 5-зонной фазовой пластинки, изготовленной из плавленого кварца (SiO 2 ) с n 1 = 1,5 и имеющей следующие размерные параметры: D = 1,5 мкм, d e =300 нм, f d = 500 нм, что соответствует числовой апертуре NA = 0,8. Поперечный и продольный профили интенсивности показаны на рис. 2 а и рис. 2 б соответственно.

Как видно, область фокусировки мезоволновой ЗП имеет высокую пиковую интенсивность I m = max{| E | 2 }=45,9 и достаточно компактные пространственные размеры: глубину фокуса DOF = 587 нм, т.е. порядка 1,2 X , и субволновую поперечную полуширину w =301 нм, что составляет ~0,6 X . Реальное фокусное расстояние ЗП f равняется 0,574 нм, т.е. несколько больше расчётного значения f d = X .

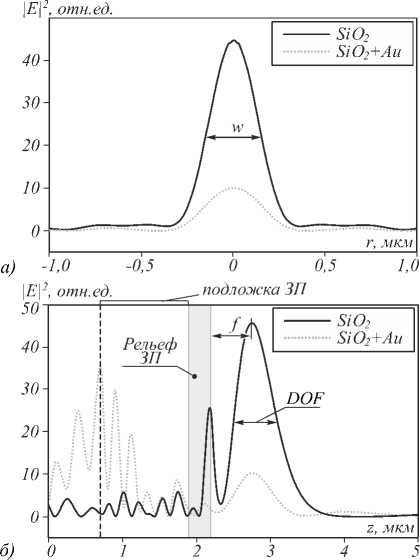
Рис. 2. Поперечный (а) и продольный (б) профили интенсивности оптического поля при освещении фазовой (сплошные кривые) и амплитудной ЗП (пунктирные кривые) циркулярно поляризованным излучением

Этот факт хорошо известен и связан с тем, что для фазовой ЗП характерно не гашение, а утилизация чётных (нечётных) п -смещённых зон. Таким образом, оптическое поле от них приходит в зону фокуса в фазе с полем от нечётных (чётных) зон. Очевидно, оптимальный фазовый сдвиг 5ф соседних зон должен составлять как раз п , что достигается определённым выбором глубины канавки [29]. Тогда, с учётом возможного заполнения канавок буферным материалом, имеем выражение для определения требуемой глубины канавки d_e ^* фазовой ЗП:

d * = X[ 2 ( n i - Re { m 2 } ) ]^{- 1}. (2)

Рассуждая аналогичным образом, получим, что оптимальная фокусировка будет наблюдаться также для всех глубин канавок пластинки c d* =( 2 p -1) d*, где p = 1,2... - целые числа. Следует отметить: несмотря на то, что выражения (1) и (2) получены из геометрооптических соображений и не учитывают волновую природу дифракции света, которая особенно ярко проявляется при масштабах рассеивателей, сравнимых с длиной волны излучения, эти выражения хорошо работают даже для субволновых значений фокусного расстояния [12].

Зависимость параметров области фокуса показана на рис. 3 а , б для ЗП, изготовленной из кристаллического оксида титана (TiO 2 ) и имеющей показатель преломления n 1 = 2,71 на длине волны 500 нм [30]. По оси абсцисс на данном рисунке отложен дополнительный фазовый сдвиг волны Δφ e = π d e d e * соседних зон, возникающий за счёт наличия фазовой ступеньки.

Как видно из рис. 3, выражение (2) достаточно точно предсказывает положение двух главных максимумов в функциональной зависимости I m ( Δφ e ), которые наблюдаются вблизи значений фазового сдвига Δφ e = π и 3 π , и провала при Δφ e =2 π . При этом пиковые значения фокальной интенсивности обеих ЗП примерно в три раза выше аналогичной величины, реализующейся при использовании амплитудной ЗП, когда чётные зоны диэлектрической матрицы TiO 2 закрыты золотым напылением. Значения рассматриваемых параметров фокуса такой амплитудной ЗП отмечены на рисунках штриховыми линиями соответствующих цветов.

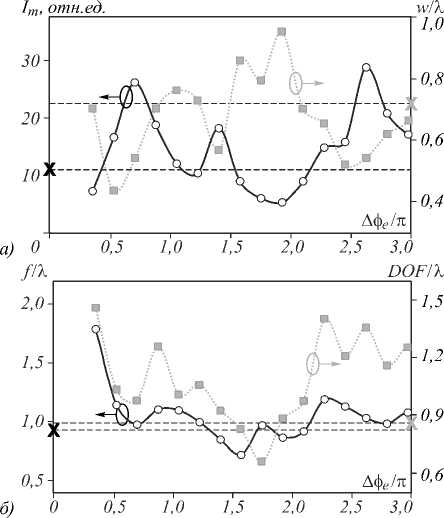
Рис. 3. Зависимость параметров фокуса ЗП от фазового сдвига ступенек Δφ e : пиковая интенсивность I m и поперечная полуширина w (а), фокусное расстояние f и глубина фокуса DOF (б). Штриховыми черными и серыми линиями показаны соответствующие значения для амплитудной ЗП с золотым напылением

Что касается масштабных параметров пятна фокусировки мезоволновых фазовых ЗП, то в целом их поведение с изменением фазового сдвига Δφe укладывается в рамки векторной дифракционной теории субволновых фазовых ЗП, представленной, например, в [27, 31]. Так, поперечный размер фокуса w (рис. 3а) принимает минимальные значения w < λ /2 в области фазовых сдвигов, соответствующих главным максимумам интенсивности, и резко повышается практически до уровня w = λ в диапазоне величин Δφe ≈ 2π, дающих деструктивную интерференцию поля соседних фазовых зон пластинки. Эта величина меньше теоретического предела пространственного разрешения амплитудной ЗП [32], радиусы зон которой рассчитывались в параксиальном приближении (без учёта квадратичного члена в (1)): w*=2πr12IrN , который для рассматриваемой геометрии составляет: w* ≈ 0,6λ.

Кроме того, из рис. 3 б следует, что реально наблюдаемый фокус пластинки f сначала располагается дальше, чем его расчётное значение ƒ d , и становится близким к нему только при Δφ e ≥ π , демонстрируя осцилляции около уровня f = λ . Характер зависимости глубины фокуса DOF, определённого по половинной интенсивности, от фазового сдвига ступенек (рис. 3 б ) повторяет аналогичное поведение фокусного расстояния. Значения DOF варьируют примерно от полутора длин волн до полуволны в рассматриваемом диапазоне изменения глубины канавок пластинки d e .

Важно отметить, что при слишком мелком рельефе ступенек пластинки d e <<  λ /2 n 1 аномальная удалённость и протяжённость фокуса связана не столько с наличием фазовых зон, сколько с ближнепольной фокусировкой оптической волны самой цилиндрической диэлектрической матрицей. Зонная структура начинает «работать» только при Δφ e >  π /2. Немонотонный характер зависимости параметров ЗП от глубины травления указывает на проявление структурных резонансов, которые могут возбуждаться внутри ЗП и модифицировать пространственную структуру ближнего поля рассеяния. Очевидно, что сама цилиндрическая подложка пластинки может быть рассмотрена как мезоразмерная резонансная полость типа плоскопараллельного резонатора Фабри–Перо, который поддерживает множество собственных электромагнитных мод с длинами волн λ j =2 D / j , где j – целые числа.

Действительно, как следует из рис. 4, при изменении толщины подложки D интенсивность в области фокуса демонстрирует эквидистантные экстремумы. Максимумы фокальной интенсивности расположены вблизи значений толщины, кратной λ 1 /2 = λ n 1 /2, а минимумы смещены на четверть волны. Наличие рельефа на поверхности диэлектрической пластинки в виде цилиндрических канавок приводит к усложнению структуры собственных колебаний подложки. Важно, что положение фокуса ЗП f при изменении толщины подложки варьирует достаточно слабо, в пределах 20% около расчётной величины f d , а само фокальное пятно остается субволновым, w ≈ λ /2 .

Фокусировка излучения фазовой ЗП с иммерсионным слоем

Подложка ЗП может быть использована в качестве иммерсионной среды, как и в обычной ближнеполе- вой микроскопии, для повышения пространственного разрешения области фокусировки [33]. Для этого зонную пластинку необходимо развернуть так, чтобы излучением освещалась поверхность с микрорельефом, а фокусировка поля проходила через более плотную среду подложки. Однако, как показано в [34, 35], такая схема фокусировки не приводит к существенным изменениям поперечного размера фокального пятна, а главным образом удлиняет фокальное расстояние f и повышает протяжённость (глубину резкости) фокуса.

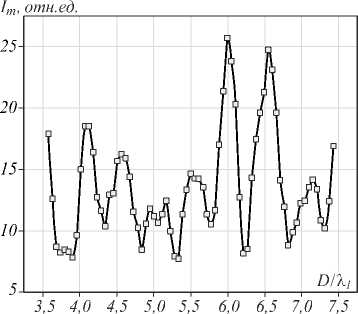
Рис. 4. Интенсивность I m в фокусе фазовой ЗП (TiO 2 , d e = 100 нм) в зависимости от толщины подложки D

Вместе с тем ситуация становится качественно иной, если несколько изменить дизайн ЗП, как показано на рис. 5 а . Здесь в качестве подложки используется усечённый конус, а сам микрорельеф ЗП рассчитывается по заданному фокусному расстоянию f для длины волны падающего излучения с учётом показателя преломления подложки: λ 1 = λ / n 1 . При условии ƒ ≈ D h , где D h – высота конуса, фокус такой иммерсионной ЗП (ИЗП) будет расположен прямо на верхней грани структуры. В данной конфигурации ИЗП эффективно концентрирует как лучи, приходящие на ось симметрии под большим углом дифракции, так и затухающие волны вблизи теневой поверхности ЗП в фокусе.

Это видно на примере расчёта двумерного распределения интенсивности ближнего поля для перевёрнутой кварцевой ИЗП с конической подложкой, показанного на рис. 5 б . При этом формируется два фокуса, дальний из которых расположен на границе «под-ложка–воздух» и имеет наибольшую интенсивность. Сравнение поперечной полуширины фокального пятна w , производимой ИЗП с радиусом навершия R h =980 нм, обычной ЗП и кварцевой сферой с таким же диаметром (3,2 мкм) соответственно, и показано на рис. 6. Эти результаты однозначно указывают на преимущество предлагаемого дизайна ИЗП. Как и ожидалось, размер фокуса ИЗП приблизительно в n 1 раз меньше, чем у стандартной ЗП и составляет суб-дифракционую величину: w ≈ λ / 2,5 .

Свободным параметром рассматриваемой иммерсионной ЗП, позволяющим оптимизировать её свойства, является радиус верхнего основания коническо- го навершия Rh, задающий угол наклона боковой поверхности конуса. Как показывает наше моделирование, его значение ключевым образом влияет на качество фокусировки ЗП. Зависимость интенсивности и полуширины фокуса ИЗП от отношения радиусов верхнего и нижнего оснований навершия ξ = Rh / rN представлена на рис. 6. Видно, что в определённом диапазоне значений данного параметра, примерно от ξ = 0,55 до 0,65 (выделен штриховкой на рисунках), реализуется субдифракционный размер фокального пятна и одновременно высокая фокальная интенсивность.

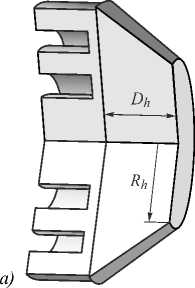
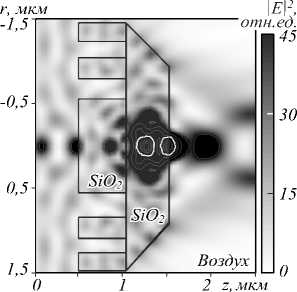
Рис. 5. Конструктивная схема ИЗП с коническим навершием (a); двумерное распределение интенсивности |E|2 поля вблизи кварцевой ИЗП (б). Освещение структуры, как и на рис. 1a, осуществляется слева

Анализ векторного распределения усреднённой по времени плотности потока энергии (вектора Пойн-тинга) P =( c /8 π ) E × H ( E и H – электрический и магнитный вектора поля соответственно; c – скорость света) показал, что существует глобальное движение энергии, которое организуется при определённом наклоне боковой стенки конуса, когда вследствие полного внутреннего отражения внутри навершия формируется резонансная полость. Основные потери энергии из этого специфического резонатора реализуются вблизи оптической оси пластинки, где за счёт встречного взаимодействия проходящего и циркулирующего энергопотоков появляются локальные зоны резкой смены направления движения оптической энергии, где происходит зарождение оптических вихрей. Один из этих вихрей локализован вблизи верхней грани зонной структуры, что способствует суперлокализации поля в области внешнего фокуса [36, 37].

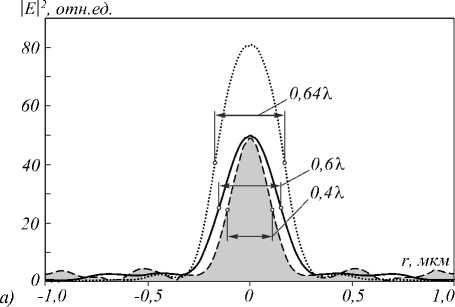
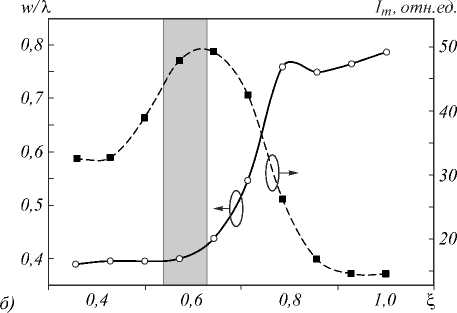
Рис. 6. Сравнение поперечной полуширины фокального пятна w, производимой ИЗП, обычной ЗП и кварцевой сферой с таким же радиусом (r N = 1,6 мкм) (а); полуширина w и интенсивность I m фокуса кварцевой ИЗП в зависимости от относительной ширины навершия ξ (б)

Следует подчеркнуть, что во всех схемах фокусировки с использованием иммерсионного слоя выигрыш по пространственному разрешению растёт пропорционально отношению показателей преломления иммерсионной среды и среды, где реализуется фокусировка поля. Так, в случае, рассмотренном на рис. 6, когда использовалась кварцевая ЗП с кварцевым же «навершием» и n 1 = 1,5, размер фокального пятна получился в полтора раза меньше, чем для «классической» ЗП в воздухе. Если в качестве материала пластинки выбрать оптически более плотный материал, например, кремний (Si) с n 1 = 4,29 на длине волны 500 нм [30] (поглощение излучения можно не учитывать в силу малости суммарной толщины структуры), то можно достичь ещё большей локализации оптического поля.

Действительно, проведённое нами параметрическое исследование позволило определить оптимальную конфигурацию иммерсионной зонной пластинки из кремния с расчётным фокусным расстоянием f d = 500 нм: радиус внешней зоны r N =687 нм, глубина рельефа d e =60 нм, высота иммерсионного кремниевого конуса D h =400 нм. В таком конструктиве ИЗП при реальном фокусном расстоянии f = D h ( NA = 3,7) даёт фокусировку излучения на своей выходной грани в пятно с полушириной w = 0,072 нм, т.е. порядка λ /7. Эта величина меньше дифракционного предела Рэлея с учётом иммерсионной среды [2]:

w * = 0,61 λ / n 1 sin α ≈ λ / 5,84, где α – угол между оптической осью и волновым вектором. При этом существенно, поскольку облучающая волна является циркулярно поляризованной, то фокальное пятно представляет собой круг.

Заключение

Таким образом, с помощью численной FEM-методики проведено моделирование прохождения оптической волны через бинарную фазовую зонную пластинку Френеля с размерами порядка нескольких длин волн излучения и изучена пространственная структура области фокуса. Показано, что глубина травления канавок пластинки, а также толщина подложки существенным образом влияют на интенсивность и масштабные параметры пятна фокусировки. Наилучшая фокусировка реализуется при глубине травления, соответствующей фазовому набегу соседних зон пластинки, в диапазоне от π /2 до π . Существенного улучшения параметров фокуса и сокращения размеров фокального пятна ниже дифракционного предела можно достичь при использовании ЗП в комбинации с иммерсионным слоем в форме усечённого конуса. Отметим, что в силу масштабируемости уравнений Максвелла полученные результаты могут быть расширены на другие диапазоны, в том числе СВЧ и терагерцовый [38].

В то же время заметим, что для ЗП с высокой числовой апертурой эффективность фокусировки излучения может несколько снижаться из-за эффекта геометрического экранирования зон [39].

К возможным сферам практического применения рассмотренного конструктива мезоволновых фазовых ЗП можно отнести устройства оптофлюидики, в которых ЗП используются в качестве рентабельных и компактных средств для направления и передачи света на сенсоры [23], элементы микроскопии и рентген-литографии высокого разрешения [25, 40, 41], прецизионное оптическое манипулирование микро- и нанообъектами [42, 43], металинзы [44], микроскопию [45, 46].

Вклад авторов

Ю.Э. Гейнц – создание COMSOL-модели и написание черновика статьи, Е.К. Панина – численное моделирование, И.В. Минин и О.В. Минин – инициирование работы и идея концепции ИЗП, Ю.Э. Гейнц, И.В. Минин и О.В. Минин – обсуждение результатов, редактирование статьи.

Работа частично выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию ИОА СО РАН в части моделирования мезоволновой ЗП и частично в рамках Программы повышения конкурентоспособности Томского политехнического университета.