Управление деформацией сдвига и ее роль в формировании напряженного и деформированного состояний (НДС)
Автор: Судаков Николай Владимирович
Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy
Рубрика: Обработка металлов давлением. Технологии и машины обработки давлением
Статья в выпуске: 3 т.17, 2017 года.
Бесплатный доступ
На основе единой математической модели обобщены варианты осадки прямоугольной заготовки с различными схемами действия напряжений контактного трения. Методом минимизации невязок при решении переопределенной системы уравнений определены поля напряжений и скоростей. Показана возможность эффективного влияния на НДС путем целенаправленного управления схемой действия контактного трения, что может оказаться полезным при снижении усилия деформации, формировании структуры материала, уплотнении некомпактных материалов и при решении каких-либо других специальных задач. Впервые показано влияние крутящего момента от сил трения при несимметричной осадке на характер напряженного и деформированного состояний в объеме заготовки. При этом, в частности, установлено наличие зон затрудненной деформации и их смещение к краям заготовки по мере увеличения степени несимметрии схемы действия внешнего трения. Показано, что влияние крутящего момента на НДС растет с увеличением коэффициента трения и отношения продольных размеров заготовки к ее высотным размерам. Выполнена сравнительная оценка неоднородности деформации при симметричной и несимметричных вариантах осадки, которая оказалась неоднозначной, а зависящей прежде всего от соотношения размеров заготовки и коэффициента трения. Сделаны рекомендации по использованию метода минимизации невязок при решении переопределенной системы уравнений в задачах по анализу НДС при обработке материалов давлением. Проиллюстрирована его эффективность, сочетающая простоту с достаточно высокой точностью по сравнению с вариационным методом.
Осадка, деформация, напряжения, трение, момент крутящий, сила, симметричная, несимметричная, эпюра, минимизация, невязка, переопределенная, система, уравнения
Короткий адрес: https://sciup.org/147157108
IDR: 147157108 | УДК: 621.771 | DOI: 10.14529/met170312
Текст научной статьи Управление деформацией сдвига и ее роль в формировании напряженного и деформированного состояний (НДС)
Целенаправленное управление напряженно деформированным состоянием в объеме заготовки при обработке давлением является одним из перспективных направлений влияния на энергосиловые параметры процесса и качество изделий. Примером тому может служить процесс прокатка-волочение [1], позволяющий существенно снизить давление при обработке листов в холодном состоянии, процесс прессования с активными силами трения, многообразие способов уплотнения некомпактных материалов, имеющих своей целью повышение плотности и ее однородности по объему. Характер НДС в объеме деформируемого тела определяется граничными условиями, среди которых напряжения контактного трения играют первостепенную роль. Вместе с тем вопросам управления схемой действия напряжений трения и как следствие деформацией сдвига на основе каких-либо технических приемов и теоретического обоснования их эффективности уделяется недостаточное внимание. Настоящая работа ставит своей целью в определенной мере дополнить имеющуюся информацию по затронутой проблеме.
В рамках единой математической модели покажем влияние схемы действия напряжений трения на НДС в объеме тела. Поставленную задачу решим на примере сжатия заготовки из идеально пластичного материала в условиях плоской деформации при различных схемах действия напряжений трения (рис. 1). Напряжения трения представим линейными зависимостями от координаты х :
Т 1 ( x ) : = ЦТ ,
Т 2 ( x ) : = ЦТ s
Y + x ( У- 1 ) b
Y-X (Y- 1 )
где ц - коэффициент трения; т s - сопротивление материала пластической деформации
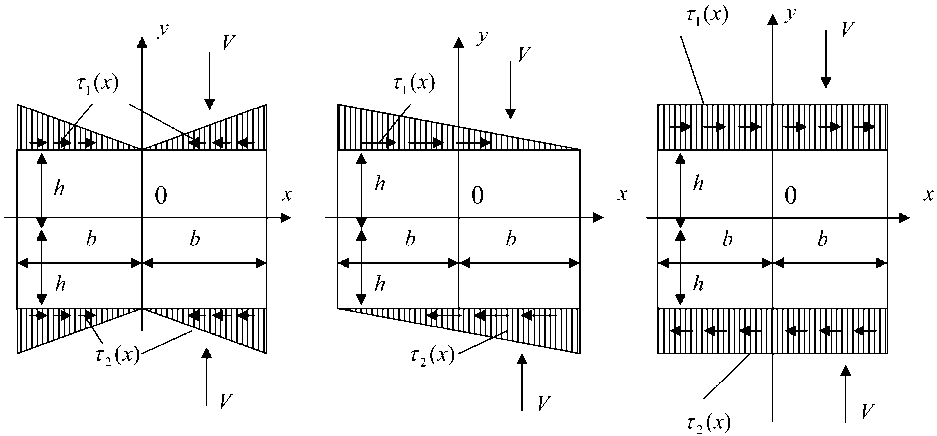
а) б) в)
Рис. 1. Некоторые из возможных вариантов эпюр трения при осадке заготовки прямоугольного сечения: а - симметричная осадка ( у = 0 ); б - несимметричная осадка ( у = 0,5 ); в - предельный случай несимметричной осадки ( у = 1 )
при чистом сдвиге; у - безразмерный коэффициент, определяющий характер эпюры трения.
При у = 0 эпюра соответствует симметричной осадке (рис. 1, а); при у = 0,5 - несимметричной осадке (рис. 1, б); при у = 1 -предельному случаю несимметричной осадки (рис. 1, в), а при 0 <у< 1 - промежуточным вариантам несимметричной осадки. Практическая реализация показанных на рис. 1 вариантов осадки возможна путем использования специальных технических приемов, например, перемещением инструмента не только в вертикальном, но и горизонтальном направлении с определенными скоростями (на рис. 1 не показано).
В основу разработки математической модели положен метод минимизации невязок при решении переопределенной системы уравнений, предложенный в работе [2].
Суть метода состоит в следующем. После выполнения всех формальных процедур, свойственных прямым вариационным методам, предлагаемый метод взамен минимизации соответствующих функционалов варьируемые параметры находит из решения переопределенной системы тех уравнений, которые не были удовлетворены на стадии формирования статически допустимых напряжений и (или) кинематически возможных скоростей. Такими уравнениями могут быть любые из замкнутой системы уравнений МСС, включая граничные условия, условие несжимаемости и другие возможные ограничения.
Касательные напряжения a xy зададим степенным полиномом, ограничившись членами четвертой степени
2 24
a xy = a 1 + а 2 x + a3 xy + a 4 У + a5x +
+ a 6 xy 3 + a 7 x 2 y 2 + a 8 x 3 y + a 9 y 4, (2)
где a i – параметры, подлежащие определению.
При симметричной и несимметричной осадке должны выполняться условия a i+x = a । x j |+y j |-y и a l x = a I x - условия асимметрии. Усло-j |-y j |+y вия асимметрии будет выполняться, если суммарная по х и у степень отдельных членов ряда (2) будет четной (xy, x2 , xy3 и т. д.). По этой причине из ряда (2) исключены члены с нечетной суммарной по х и у степенью. Удовлетворив граничные условия для axy :
a xy|y = h -T 1 ( x ) = 0 и a xy|y =- h -T 2 ( x ) = 0 , (3)
нашли a2, a3, a4, a5, a7, a8. При этом использовали метод неопределенных коэффициентов (группировка членов уравнения по степеням независимой переменной и приравнивание нулю выражений при разных степенях независимой переменной). В результате получили o xy (x, y, al, a6, a9).(4)
Из дифференциальных уравнений равновесия для плоской деформации:
Sc do doxx + dxdy
SoxvSo xy +yy = о dxdy
определили нормальные напряжения o xx и o yy с точностью до неизвестных функций интегрирования f ( y ) и f ( x ) , которые представили отрезками степенных рядов:
f ( у ) = a w + a n у 2 + a 12 у 4 ; (7)
f ( x ) = a13 + a14 x 2 + a15 x 4. (8)
Константу a 7 нашли из условия равенства нулю интегральной суммы продольных напряжений на границах заготовки ( x = b и x =— b ): h
J o xx ( b , у , a 1 , a 6 , a 9 , a 10 , a ll , a 12 ) dy = 0. (9)
-
- h
Константу a 12 определили из условия равенства нулю суммы моментов внешних сил, действующих на заготовку, b
Myy = J o yy i y = h ■xdx ;
— b
b
M т = J t 1( x ) • hdx ,
— b
где Myy – крутящий момент от нормальных напряжений oyy , действующих на контакте с инструментом; Mт - крутящий момент от напряжений трения.
В итоге задача свелась к определению восьми констант ( a 1, a 6, a 9, a 10, a 11, a 13, a 14, a 15 ) при наличии неудовлетворенного условия пластичности:
o xx ( x , y , a 1 , a 6 , a9, a w, a B) —
-
— o yy ( x , y , a 6 , a 13 , a 14 , a 15 ) —
o^ ( x , y , a ,, a 6, a 9 )2
-
— 2 т 1-- xy 2 6 9 = 0. (11)
V t .
Для удобства дальнейших выкладок представим уравнение (11) следующим образом: ^ ( x , y , a 1 , a 6 , a 9 , a 10 , a 11 , a 13 , a 14 , a 15 ) = 0 . (12)
В соответствии с методом, предложенным в работе [2], тело заготовки разбили равномерной прямоугольной сеткой, включающей 25 узлов с конкретными координатами, для которых записали уравнение (12). В результате решалась система из 25 уравнений при восьми неизвестных параметрах. Переопределенная система уравнений приближенно решалась относительно параметров a i с помощью программы, минимизирующей невязки. Такую программу, в частности, реализует встроенная в Mathcad функция Minerr . Ниже предлагается вниманию блок программы, ответственный за минимизацию невязок при решении переопределенной системы уравнений (рис. 2), а также фрагменты результатов

Рис. 2. Фрагмент программы, минимизирующей невязки
расчета, выполненного для условий: h = 50 мм; b = 100мм; µ= 0,4; τ s = 300МПа (рис. 3–6).
При этом левый ряд рисунков характеризует НДС при симметричной осадке ( γ = 0), а правый – при несимметричной осадке ( γ = 1). Для других возможных вариантов несимметричной осадки НДС будет иметь промежуточный характер между представленными на рисунках крайними случаями. На рис. 3 показаны эпюры относительных нормальных напряжений ( σ yy / σ s ) при симметричной осадке ( γ = 0) и несимметричных вариантах осадки. Полученные результаты подтверждают имеющиеся представления о симметричной осадке. Что касается несимметричных вариантов, то в литературе отсутствует информация о полях напряжений, корректно учитывающих специфику процессов. В частности, в известных решениях не учитывается крутящий момент, обусловленный внешними силами трения. Необходимость уравновешивания крутящего момента приводит к несимметричному распределению нормальных напряжений на противоположных контактных поверхностях. Анализ показал, что с увеличением отношения b / h влияние крутящего момента на асимметрию напряженного состояния ослабевает. Следует также заметить, что относительное среднее усилие деформации ( P c / σ s ) при γ = 0, γ = 0,5 и γ = 1 для указанных выше условий расчета соответственно составило: 1,26; 1,18 и 1,02, а при b / h = 8 : 1,75; 1,44 и 1,08. Эти результаты также не противоречат имеющимся представлениям.
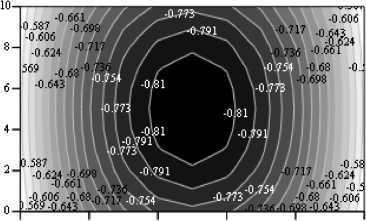
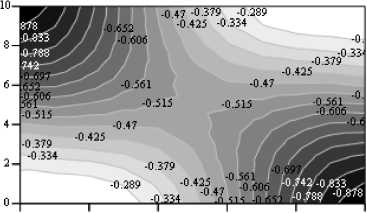
На рис. 4 показаны карты линий уровня относительного значения среднего нормального напряжения ( Kσ = σ / σs ); (здесь σ – среднее нормальное напряжение, а σs = 3 ⋅ τs ). Имеет место изменение неоднородности напряженного состояния по мере увеличения степени не симметрии (увеличение γ от нуля до единицы). Так, при γ = 0 максимальное отклонение K σ от среднего значения составило 22 %, а при γ = 1 – 79 %. Таким образом, для условий расчета ( b / h = 2 ) неравномерность напряженного состояния оказывается не в пользу несимметричной осадки. При увеличении отношения b / h картина меняется в пользу несимметричной осадки, например, при b / h = 10 соответственно имеем 56 и 9,5 %. Это можно объяснить тем, что с увеличением b / h увеличивается плечо крутящего момента нормальных напряжений по сравнению с плечом напряжений трения, что и способствует более эффективному уравновешиванию момента от напряжений трения. Заметим, что математические модели, не учитывающие крутящие моменты, всегда приводили к более однородному напряженному состоянию при несимметричной осадке. Таким образом, влияние схемы действия сил трения (деформации сдвига) на качественную картину напряженного состояния достаточно очевидно.
Поле скоростей при известном напряженном состоянии определили из физических уравнений [3]:
σ = τ ξ xx + σ ;
xx s H
ξ yy
σyy =τs H +σ
σ xy
=τ s
ξ xy H ,
где ξij – компоненты тензора скоростей деформаций сдвига, связанные со скоростями течения ϑi (ϑx,ϑy) известными геометриче- скими уравнениями ξij = 0,5(ϑi, j + ϑj,i) ; Н – интенсивность скоростей деформаций сдвига (H=2 ξ + ξ ).
xx xy
После определения ξij убедились, что условие несжимаемости ( ξ + ξ = 0) выпол-xx yy няется автоматически. Функцию интегрирования f (x) при решении геометрического уравнения относительно скорости ϑy (x, y)
нашли, удовлетворив граничное условие ϑy (x, h) = -V (здесь V – скорость инструмента). Условие ϑy (x, -h) = V выполнилось автоматически. Функцию интегрирования f (y) при решении геометрического уравнения относительно ϑx (x, y) задали отрезком степенного ряда с неизвестными коэффициентами, которые определялись из равенства ξxy - ξxyv = 0, т. е. из равенства ξxy , полученной из физического уравнения, значению ξxyv , полученной из геометрического уравнения на основе заданного поля скоростей. При этом использовали метод минимизации невязок при решении переопределенной системы уравнений.
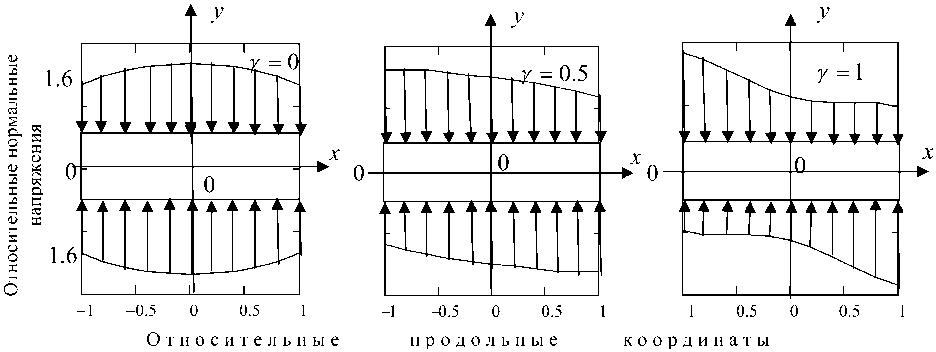
Рис. 3. Эпюры нормальных напряжений на контакте с инструментом
у = О
/ = 1
О 2 4 б 8 10
0 2 4 б 8 10
min(Kc>) = -0.828 mean(Ko) = -0.706 ma^Kcy) = -0.55
min(Ka) = -0.924 mean(Ka) = -0.516 ma^Ka) = -0.243
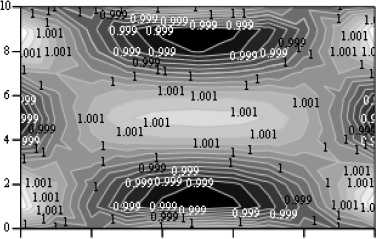
О 2 4 6 8 10
Рис. 4. Карты линий уровня средних нормальных напряжений
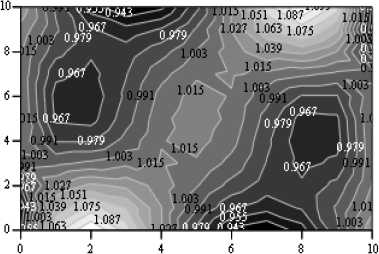
КН min(KH) = 0.998
mcan(KH) = 1 ma^KH) = 1.002
KH min(KH) = 0.931
mean(KH) = 1 ma Рис. 5. Карты линий уровня интенсивностей скоростей деформации сдвига На рис. 5 представлены карты линий уровня относительного значения интенсивности скоростей деформаций сдвига H/H0 (здесь H0 – интенсивность скоростей деформаций сдвига при однородной деформации). Темные участки на рис. 5 показывают наличие зон затрудненной деформации (интенсивность скоростей деформаций сдвига меньше, чем при однородной деформации). По мере увеличения степени не симметрии (увеличение γ) области затрудненной деформации смещаются к краям заготовки (см. рис. 5), а не исчезают Рис. 6. Векторные диаграммы поля скоростей вообще, как это показывают решения, не учитывающие наличие крутящих моментов. Векторные диаграммы полей скоростей на рис. 6 иллюстрируют характер течения металла при симметричной и несимметричной осадке. Заключение 1. На основе единой математической модели обобщены различные варианты несимметричной, включающей симметричную как частный случай, осадки заготовки прямоугольного сечения из идеально пластичного материала для условий плоской деформации. 2. Методом минимизации невязки при решении переопределенной системы уравнений [2] определены поля напряжений и скоростей для возможных вариантов несимметричной осадки. Максимальная ошибка при приближенном удовлетворении условия пластичности составила при у = 0 порядка ±0,2%, при у = 0,5 - ±5%, а при у = 1 -±10%. Можно предположить, что величина ошибки зависит от числа членов ряда уравнения (2), степени переопределения системы уравнений и каких-либо других факторов. Этот вопрос требует изучения. 3. Показано достаточно существенное влияние схемы действия напряжений трения (деформации сдвига) на напряженное и деформированное состояние в объеме заготовки. Практическое значение этого положения состоит в целесообразности целенаправленного управления деформацией сдвига при необходимости, например, снижения усилия деформации, регулирования структуры, уплотнения некомпактных материалов и решения каких-либо других специальных задач. Ранее подобной сложности задача могла быть решена только вариационным методом [3], существенно более трудоемким в реализации. Автор выражает надежду, что метод минимизации невязки при решении переопре- деленной системы уравнений заинтересует определенный круг научных работников и тем самым получит дальнейшее применение и развитие.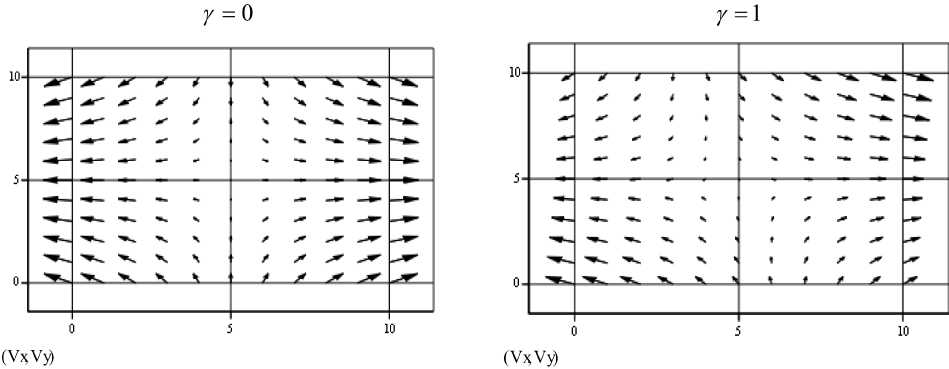
Список литературы Управление деформацией сдвига и ее роль в формировании напряженного и деформированного состояний (НДС)
- Выдрин, В.Н. Принципиальные и теоретические основы нового процесса «прокатка-волочение»/В.Н. Выдрин, Л.М. Агеев//Теория и технология прокатки. -Челябинск: ЧПИ, 1971. -№ 76. -С. 3-21.
- Судаков, Н.В. Дискретно-локальный метод минимизации невязок при приближенном решении уравнений в задачах обработки металлов давлением/Н.В. Судаков//Наука ЮУрГУ: материалы 66-й научной конференции Секции технических наук. -2014. -С. 1669-1675. -http://dspace.susu.ru/xmlui/bitstream/handle/0001.74/4356/18.pdf.
- Колмогоров, В.Л. Механика обработки металлов давлением: учеб. для вузов/В.Л. Колмогоров. -М.: Металлургия, 1986. -688 с.


