Управление динамическими свойствами механических систем, выполненных из smart-материалов на основе пьезоэлектриков

Application of composites materials involving piezoelectric elements in engineering systems offers considerable scope for optimization of their mechanical characteristics. He propose to solve this problem by means of embedding piezoelectric elements into the body of shell to achieve vibration suppression through dissipation of energy in external RLC-citxuib. Complex eigenfrequencies obtained consist of the realpart, which is vibration frequent \. and the imaginary part— damping index. Complex eigenvector contains the vibration mode shape and phase. The approach of piecewise linear normal with the use of kinematic shell iheorv for each layer were used to handle the essentially different physical properties of layers Computations performed for shells of arbitrary spatial geometry showed effectiveness of the proposed method of control of dissipative properties.

Новые технологии в производстве композитов породили такое понятие, как SMART-материалы. Основной особенностью таких материалов является их способность целенаправленно изменять свои свойства в зависимости от внешних условий. Как правило, в состав SMART-композитов входят датчики, фиксирхюшие изменение параметров окружающей среды или термомеханическое состояние конструкции, и активные элементы, так называемые актуаторы, которые в нежном направлении изменяют механические свойства конструкции. Такой тип S.MAR Г-материалов является активным и подразумевает наличие цепей обратной связи и систем управления актуаторами.

Наиболее часто для изготовления SMART-композитов используются пьезоэлектрические материалы. В частности, это объясняется наличием у них прямого и обратного пьезоэффекта, что позволяет использовать пьезоэлементы как в качеове датчиков, так и в качестве актуаторов. В настоящее время наибольшее распространение поточили пьезокерамические материалы на основе титаната бария и цирконата -титаната свинца.

Для решения проблем, связанных с вибрациями конструкций, нами предлагается использовать полуактивные SMART-материалы на базе пьезокерамики, в которых функции датчиков и актуаторов совмещены. Для этого электродированные поверхности пьезоэлементов, расположенных в определенных местах конструкции, соединяются пассивными Я£С-цепями с точкой нулевого потенциала. Принцип гашения вибраций основан на преобразовании механической энергии в электрическою с ее последующем рассеиванием во внешних Л£С-цепях в виде тепла и электромагнитного излучения.

Наибольший эффект от использования полуактивных SMART-материалов достигается при решении задач оптимизации динамических свойств оболочечных элементов конструкций.

Диссипативные свойства конструкции могут быть определены из решения спектральной задачи теории злектровязкоупругости. Для большинства конструкционных материалов спектральная задача теории злектровязкоупругости может быть сформулирована в форме с комплексными динамическими модулями, являющимися аналогами дифференциальных и интегральных операторов в физических соотношениях (работы А.С. Кравчука, В.П. Матвеенко, Е.П. Клигмана, В.В. Болотина. Ю.Н. Новичкова), и комплексными сопротивлениями внешних электрических RLC- цепей.

В этой постановке найденные комплексные собственные значения будут определять частоты собственных колебаний и показатели демпфирования, Комплексные частоты и формы собственных колебаний зависят не только от конструктивных и технологических особенностей оболочечных систем, но и от типа и способа электрического соединения (RLC- параметры) пьезоэлементов конструкции. Целенаправленное изменение этих параметров позволит оптимизировать динамические характеристики (резонансные частоты, формы собственных колебаний и показатели демпфирования) системы

Вариационное уравнение движения тела, обладающего пьезоэлектрическими свойствами

Вариационное уравнение движения тела, состоящего из упругого Д и пьезоэлектрического Ц элементов, может быть получено на основе соотношений линейной теории упругости и квазистатических уравнений Максвелла. В случае изотермического процесса и при отсутствии внешних сил вариационное уравнение может быть записано следующим образом:

|(сг^8Еу.+рм'5гг, ^К+j^av3ey--D'8E,+рм'5и, рК- j ^ocpt/Q = О, (Г)

где ст. е - тензоры напряжений и деформаций; и - вектор перемещений; D. Е -векторы электрической индукции и напряженности электрического поля: р -плотность материала; £1р - поверхность, ограничивающая пьезоэлектрический элемент; q, и <р - поверхностная плотность зарядов и электрический потенциал.

Компоненты тензора деформаций удовлетворят соотношениям Коши

Г/

1 , -\и л-и

). Электрическое поле считается потенциальным, то есть выполняется

условие —г =   Для изотермических процессов в линейных электроупругих средах

Эх'

справедливы следующие физические соотношения:

с'^> = С^уЫЕ_к, - для У,,

(2а)

о^у = С^даЕ_ы -^^кЕ_к

,           _z. 1-дляЕ,,                    (2о>

Dk =$и Eh+e ei где Сик! - тензор упругих констант; ру* и е*' - тензоры пьезоэлектрических и диэлектрических коэффициентов.

Если элемент тела Е, обладает вязкоупругими свойствами, то согласно принципу Вольтерра тензор упругих констант С"^А/ в зависимости (2а) должен быть заменен соответствующим вязкоупругим оператором.

Уравнения электроупругости оболочек с внешними jtZC-цепями

Применение пьезоматериалов для создания оболочечных конструкций требует использования моделей оболочек, учитывающих все компоненты тензоров напряжении и деформаций. Это объясняется тем, что такие материалы, как правило, поляризованные в направлении толщины, проявляют свои пьезоэлектрические свойства при трансверсальном деформировании. Учет всех компонент тензоров напряжении и деформаций может быть осуществлен в рамках шестимодальной теории оболочек Тимошенко.

Обобщая кинематические гипотезы шестимодальной теории Тимошенко, приходим к следующим соотношениям для компонент вектора перемещений и электрического потенциала точки оболочки с Гауссовыми координатами .г" (о - 1.2) и нормальной координатой т3 = г:

«« ^^.г^иДх'^^гЧ’ДЕ,? ).

,                  .                                              (3)

и, (.Г¹ , X" , с) = w(x‘,x²) + £7]Д,Х" ),

(р ^.г1,х2,z)= / (х1,х2) + z Ф ^№,х2 ],

Здесь z/„- перемещения в направлении базисных векторов Гауссовых координат, а, - перемещения в направлении нормали, <р - электрический потенциал в точке: U ч . / - перемещения и потенциал точек поверхности приведения, Y - углы поверена нормали, р - обжатие по толщине оболочки. Ф - изменение потенциала по толщине оболочки.

При получении физических соотношений мы получили обобщенные векторы напряжений и деформаций, которые помимо механических величин содержат и электрические. Введем теперь векторы обобщенных перемещений и нагрузок.

Вариационное уравнение движения пьезоэлектрической оболочки в матричной форме будет иметь следующий вид:

где {«}={«,,«,дн,ф}^Г , [p] = diag(p, p,p,O), Д = ^t'',E зДд , Д = L^¹, - вектор обобщенных деформаций, L - дифференциальный оператор.

Квазигармонические колебания оболочек

Рассмотрим процессы, которые описываются временной функцией где СО - комплексная частота:^, - комплексная амплитуда.

Тогда вариационное уравнение (4) для амплитудных значений компонент состояния примет вид (временной множитель опущен):

((3{е}^Г [dJIe} — СО²8{г/}^Г [pjfwjjc/Q = ]8{«}^Г {с}(7ТК п                                   л

Интеграл по поверхности Q в уравнении (4) определяет электрические граничные условия для пьезоэлектрических участков оболочки.

Рассмотрим случай, когда один из пьезоэлементов с злектродированной поверхностью Q_o соединен с точкой нулевого потенциала проводником сопротивлением R, емкостью С и индуктивностью L. Для математического описания этого типа граничных условий воспользуемся законом Ома для переменного тока:

^-^RI-vLI^UrQ + LQ.              (5)

Здесь (р - потенциал и Q = J qd£l - заряд на электроде; I = Q - ток в проводнике.

«с

Так как мы рассматриваем квазигармонический процесс, то есть ф(/) = <р(]    .

то дифференциальное уравнение (5) можно разрешить относительно Q:

-to2 L-i a-R’

С учетом эквинотенциальности поверхности П. и того, что RLC является внешней цепью, будет выполняться условие

При отсутствии иных поверхностных сил. окончательно уравнение движения примет вид

[с]{_Е}-«У6{₀}^г [р]М)я_г+^МД2М_{= 0}, ' С -го L-z ож

(6*

где о0 - потенциал на злектродированной части пьезоэлемента Q . Уравнение (6)

является однородным и может рассматриваться как вариационная задача на собственные значения.

Конечно - элементная реализация поставленной задачи

Вариационная задача (6) с помощью метода конечных элементов (МКЭ) сводится к алгебраической проблеме собственных значений:

([К]~щ2М + [сН]){^             (7)

где [А']- матрица жесткости. [Л/] - матрица масс. [G] - матрица '’жесткости внешних й£С-цепей.

Условием существования нетривиального решения является

D(®) = det([A] - со2 [Л/] + ^G(co)]j = 0 .

Уравнение (7) существенно отличается от обобщенной проблемы на собственные значения наличием матрицы [б(ю) |, которая содержит нули и элементы

1 вида ---:------;----------.

С - йУ£ - itoR

Для расчета слоистых оболочек использован следующий подход, позволяющий учитывать изменение свойств материала по толщине.

Представим рассматриваемую конструкцию совокупностью п независимых однослойных оболочек. Выберем в качестве единой поверхности приведения (координатной поверхности) внутреннюю поверхность первого слоя S^R . Построим на поверхности <Н конечно-элементную сетку с одинаковой аппроксимацией всех компонент вектора перемещений.

Для каждого А-го слоя вводится свой вектор узловых параметров ^\u- . wk ,Vt,Vc'Хк * Фа IГ = {{^а-}-{^Л >Фа} и определяется соответствующая ем\ матрица жесткости [А*]. Здесь ^Uk\ включает перемещения координатной поверхности и,., ик , wk, а компонента {ЧАД— углы поворота нормали и(т. и^ и обжатие по толщине /д . Преобразуем вектор узловых перемещений нго узла для А-s о слоя к новым компонентам:

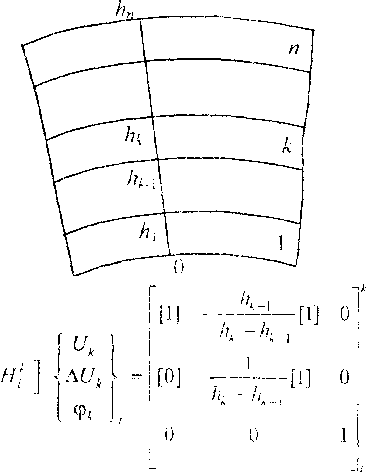
где Сд -- вектор перемещений внутренней поверхности слоя; Д(Л - приращение вектора перемещений в А-м слое; [1] и [0] - единичная и нулевая матрицы соответствующей размерности.

В результате перехода к вектору неизвестных в приращениях матрица жесткости будет определяться следующим образом:

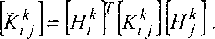
Условием совместности деформации первого и второго слоя является соотношение:

В матричном виде оно приводится ниже. Здесь учтено, что первый слой не обладает пьезоэлектрическими свойствами (узловые переменные: Е/ц AG)), а второй является

пьезоэлектриком (С^ АбА, ф): ' их mj. Г[1]   0   0   01 г 0   [1]   0   0        ' ш, ф АП,    .  . г- Ии [1] 0 о 0    0 [1] 0        2 ф L0 0 0      1 где [7)1 - матрица «склейки» 1-го и 2-го слоев.

Данное уравнение вводит новый вектор узловых параметров {Г'э]. описывающий совместную деформацию двух первых слоев. При этом матрицы жесткости этих слоев объединяются следующим образом:

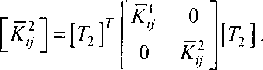
Теперь [А.Т] - матрица жесткости двух первых объединенных слоев. Аналогично вычисляются матрицы жесткости для любого числа слоев. Матрица ’часе слоистой оболочки и векторы узловых нагрузок получаются ио этой же схеме.

Численное исследование и оптимизация динамических свойств конструкции

Для иллюстрации возможностей предложенного подхода был выполнен расчо и проведена оптимизация демпфирующих свойств стальной квадратной пластинки размером 120x120x0,5 мм, защемленной по контуру. Предполагалось найти место расположения пьезоэлемента и величину сопротивления шунтирующего резистора

(емкость и индуктивность отсутствуют) для наилучшего гашения третьей моды колебаний (рис. 1). Пьезоэлемент был выполнен из керамики PZT5 и имел размер 15x15x0,5 мм.

Производился поиск оптимальных областей расположения и величин сопротивления для третьей моды колебаний. График зависимости показателя демпфирования (мнимой части комплексных собственных частот) от места расположения пьезоэлемента на пластинке

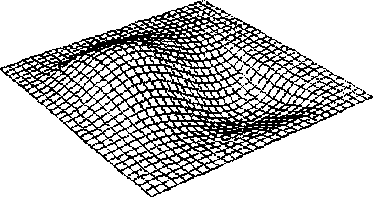
Рис. 1. Третья форма колебаний

пластинки

для третьей моды показан на рис.2. Зависимость показателя демпфирования от величины сопротивления шунтирующего резистора R в случае установки пьезоэлемента в оптимальном месте приведена на рис.З.

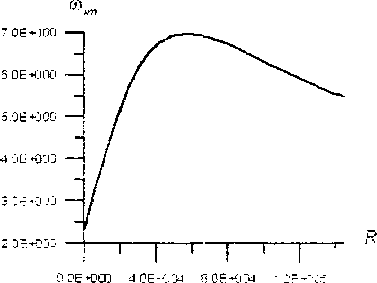
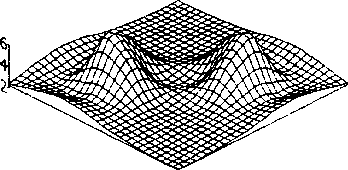
Рис.2. Зависимость показа юля демпфирования от места расположения пьезоэлемента на плас тинке для третьей моды

Рис.З. Зависимость показателя демпфирования от величины шунтирующего сопротивления А'

При расположении пьезоэлемента в оптимальной зоне показатель демпфирования может быт ь увеличен более чем в 2 раза.

Для оценки снижения резонансных амплитуд третьей моды колебании были построены амплитудно-частотные характеристики (АЧХ) различных вариантов пластинки с оптимальным расположением пьезоэлемента при возбуждении колебании сосредоточенной силой F = со^рг), приложенной на поверхности пластинки. Участок

АЧХ в окрестности третьего резонанса показан на рис. 4.

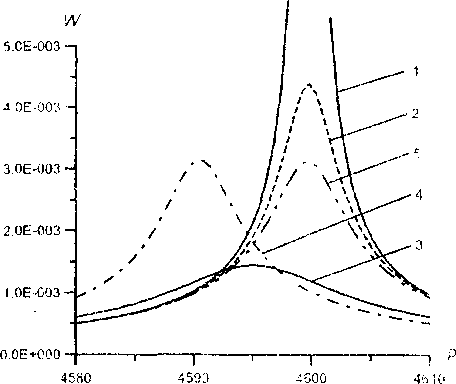
Рис. 4. Амплитудно-частотная характеристика системы с оптимальным демпфированием третьей моды колебаний

Кривые на графике соответствуют следующим вариантам:

• -    1 - колебания упругой пластинки;

• -    2 - колебания пластинки, обладающей вязкоупругими свойствами с тангенсом потерь 8 = 0,001;

• -    3 - колебания пластинки при оптимальном значении сопротивления шунтирующего резистора R=R₀;

• - 4 - колебания пластинки при значении сопротивления шунтирующего

резистора R=R„/10;

• -  5 - колебания пластинки при значении сопротивления шунтирующего

резистора R=10R_o.                                      .

Полученные результаты позволяют сделать вывод о том, что оптимальное значение сопротивления шунтирующего резистора не зависит от места установки пьезоэлемента, а определяется резонансной частотой со, на которую настроен демпфер. При этом выполняется условие равенства сопротивления внешней цепи и емкостного сопротивления пьезоэлемента R_o = l/(toC), где C = E.£₀Sjd - емкость пьезоэлемента; 5 - площадь электродированной поверхности; d - расстояние между электродами: е -относительная диэлектрическая проницаемость пьезокерамики; е₀ - диэлектрическая проницаемость вакуума.

Этот факт хорошо известен в электротехнике и говорит о том, что максимальная отдача энергии реализуется при равенстве внутреннего сопротивления источника и нагрузки.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант РФФИ № 00-01-640).