Управление движением навигационного робота мощностью приводов ведущих колес

В последнее время навигационные роботы получают широкое распространение для работы в особо опасных условиях, в том числе в горной промышленности. Алгоритмы управления ими реализуются, как правило, на основе точных аналитических выражений, которые не требуют интегрирования дифференциальных уравнений и поэтому могут быть использованы при моделировании работы навигационных систем на продолжительных интервалах времени [1, 2]. В данной работе предложен один из возможных вариантов управления роботом через мощности независимых электроприводов колес с использованием описания движения в форме Лагранжа [3, 4].

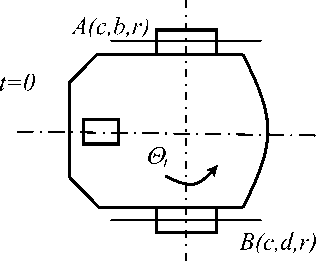
Систему отсчета наблюдателя (рис. 1а) принимаем так, чтобы в исходном состоянии оси ведущих колес робота были ориентированы вдоль оси у, а их пересечения с плоскостями симметрии колес имели координаты А(с, b, r) и В(с, d, r) . Движение робота в пространстве переменных Лагранжа можно рассматривать как наложение трех движений:

• а)    вращательного движения колес относительно собственных осей,

• б)    дополнительного вращения робота относительно оси, проходящей через произвольно выбранный полюс параллельно оси z ,   которое

возникает за счет разности окружных скоростей ведущих колес,

• в)    поступательного движения полюса.

  ^y

  
  

  О

  
  
  
  
  

  a)

  x

  
  
  
  
  

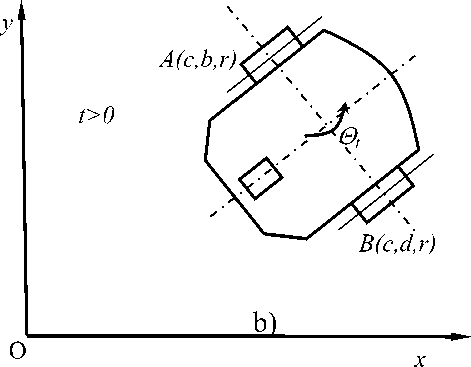
Рис 1 Исходное (a) и текущее (b) положения навигационного робота

С учетом ориентации колес в исходном состоянии, вращение принадлежащих им частиц в плоскости xOz описывают уравнения

• x = c + ( a — c )cos А ф + ( у — r )sin А ф ,

y = β ,                                      (1)

z = r — (a — c)sin Аф + (у — r) cos Аф, где a, в, у - лагранжевы (начальные) координаты рассматриваемой частицы по направлениям осей x, y и z, соответственно.

Разность угловых скоростей ведущих колес приводит к вращению относительно оси, параллельной оси z . В качестве полюса для описания этого вращательного движения можно принять точку А. Тогда уравнения внешнего наложенного движения принимают вид

• x = с + ( a — с )cos Аб — ( в — b )sin Аб ,

y = b + ( a — с )sin А б + ( в — b )cos А б ,                       (2)

z = γ .

Используя принцип суперпозиции, получаем уравнения совмещенного движения для любых частиц колес А и В с начальными координатами ( a , в , у )

• x = с + [( a — c )cos А ф + ( у — r )sin A ф ]cos А б — ( в — b )sin А б ,

y = b + [( a — c )cos А ф + ( у — r )sin A ф ]sin А б + ( в — b )cos А б ,      (3)

z = r — ( a — c )sin А ф + ( у — r )cos А ф .

Для частиц колеса А уравнения (3) за счет β=b принимают более простой вид x = с + [(a — c) cos Аф + (у — r) sin Аф] cos Аб,

У = b + [( a — c )cos А ф + ( у — r )sin A ф ]sin А б ,               (3а)

z = r — ( a — c )sin А ф + ( у — r )cos А ф .

Расстояние от любой частицы колеса В до точки А остается постоянным

( x - с )² + ( y - b )² + ( z - r )² =

{ [( a - c ) cos A ф + ( y - r ) sin A ф ]cos A O - ( в - b ) sin A O } ² +

+ { [( a - c ) cos A ф + ( у - r ) sin A ф ] sin A O + ( в - b ) cos A O } ² +

+ [ - ( a - c )sin A ф + ( y - r )cos A^ ] =

= [( a - c )cos A ф + ( y - r )sin A ф ] ² + ( в - b ) ² + [ - ( a - c )sin A ф + ( y - r )cos A ф ] ² =

= ( a - c )² + ( в - b )² + ( y - r )²

или

( x - a )² + ( y - b )² + ( z - r )² = ( a - a )² + ( в - b )² + ( y - r )² .            (4)

Траектории точек А и В , ассоциируемых с осями колес, после наложения движений «а» и «б», можно найти по приведенным уравнениям с учетом указанных выше значений переменных Лагранжа. Точка А , которая принята в качестве полюса, остается неподвижной и сохраняет координаты (см. ур - ие 3а) х = с, у = b, z = r, а точка B перемещается по окружности (см. ур-ие 3)

x = с - (d -b)sin AO,      y = b + (d -b)cos AO,   z = r(5)

или

(х - с)2 + (у - b)2 = (d - b)2,       z = r.(5а)

Будем считать, что точка А совершает поступательное движение по некоторой плоской кривой х = х(t) ,     y = y(t),     z = r = const ^ z(t) .(6)

Платформа и ось колеса В в этом внешнем движении также перемещаются поступательно в соответствии с уравнениями х = a + uA (t) ,        y = в + vA (t),        z = r = const ^ z(t) .(7)

Особо отметим, что если заданы угловые скорости, тогда компоненты перемещения точки А должны быть получены интегрированием линейных скоростей по времени. Поэтому в дальнейшем сначала находим скорости

⁽ x t ) A = ^ t r ^{cos O} ,      ⁽ y_t ) A = ^ t r sin ⁰ ,                      ⁽⁸⁾

а затем перемещения tt    tt uA (t) =J (xt) Adt = rj^t cos[0( t)]dt ,         vA (t) = J (yt) Adt = rJ^t sin[0( t)] dt .

0                 0                                                0                  0

Для простейших вариантов движения, например, для движения по кругу, интегрирование может быть выполнено в явном виде (см. ниже).

Уравнения совмещенного движения можно записать через компоненты вектора перемещения x = a + u(t) + [c - a + (a - c)cos Aф + (y - r)sin Aф]cos AO - (в - b)sin AO, y = b + v(t) + [c - a + (a - c) cos Aф + (y - r) sin Aф] sin AO + (в - b) cos AO, (10)

z = r - ( a - c )sin A ф + ( y - r )cos A ф .

При одновременном вращении обоих колес кинематические связи сводятся к дифференциальным соотношениям

r ( d ф - d y ) = Ld O  или   d O = ( r I L )( d ф - d ^ ) = ( r / L ) ф - ^ ) dt .

Отсюда находим

• ⁰ , = ( r I L Уф -Wt )    при L = V⁽ x A ^- x B )² + ⁽ У а ^- У в ^{) 2} = 1 b ^- d I •            (11)

Если изменение углов и угловых скоростей колес во времени будет известно, решение сводится к последовательному определению кинематических характеристик вращательного, а затем поступательного движения, мощности, момента и сил на осях ведущих колес

• 0, = r (Ф, - W,),     0,, = r (Ф« - Wtt),    0 = 00 + r (Ф - w),(12)

tt uA(t) = xA - aA = r Jw cos0dt,     vA(t) = Уа — Pa = rJw sin 0dt •(13)

Все последующие соотношения представлены через независимые функции угловых скоростей или углов поворота, которые определяют поведение робота в любой момент времени.

Ниже приведены уравнения для скоростей и ускорений осей колес и центра масс платформы симметричного робота при r_A = r_B = r, а с = 0,5( « а + а в ) , в = 0,5( Д + в ) :

точка А

⁽ x t ) A = W t r ^{cos 0} ,      ⁽ y_t ) A = W t r sin ⁰ ,

⁽ x tt ) A = W tt r ^{cos 0 -} W , ^{0 r sin 0} = W tt r ^cos[ r ⁽ Ф ^- W ^{)] -} r- W t ( Ф ^- W t ) ^sin[ r ⁽ Ф ^- W ^)] ,

⁽ x tt ) A = r 1 W tt ^cos[ r ⁽ Ф -W ^)] - r W t ^{Ф -} W t ) ^sin[ r ⁽ Ф - W ^)] f ,

⁽ У , ) A = W tt r ^{sin 0 +} W t ^O t r ^{cos 0} ,

⁽ У„ ) A = ^r 1 W tt ^sin[ r ⁽ Ф ^- W ^{)] +} r W t ⁽ Ф , ^- W t ) ^cos[ r ⁽ Ф ^- W ^)] f ,

t xA = a + r J wz cos Odt,

t

Уа = P a ^{+ r} J W t ^sin ^ ,

точка В xb = xa - (d - b)sin AO,    yB = yA + (d - b)cos AO,

⁽ x t ) в = ⁽ x t ) A ^{- O} t ⁽ У в ^- У а ) = ⁽ x t ) A ^{- O} t ^{( d -} b ^{)cos 0} ,

⁽ У , ) в = ⁽ У , ) а ^{+ 0} , ^{( х} в ^{- х}а ) = ⁽ у , ) а ^{- 0} , ^{( d -} b ^{)sin 0} ,

( x_tt)_B = ( x_t)_A - 0t ( d - b )cos 0 + 0 /( d - b )sin 0 ,

( У и ) в = ( Уи ) a - 0 _tt ( d - b ) sin 0 - 0 , ( d - b ) cos 0 ,

⁽ xtt ) в = ⁽ xtt ) a ^{- 0} tt ⁽ У в ^- У а ) ^{- 0} ° ^{( х} в ^{- x}a ) ,

⁽ y ,t ) в = ⁽ y ,t ) a ^{+ 0} tt ^{( х} в ^{- x} a ) ^{- 0} t ⁽ Ув ^- У а ) •

Для точки С из простых геометрических соотношений находим

1/ хС = 2( хА + хв ) , (х,)С = 1[(х,) А + (х,)В ] , (хи )С = |[(хи ) А + (хи )В ] ,

1/

У с = -⁽ У а ⁺ У в ) ,

⁽ У, ) c = ^1[( У, ) a ^{+ (} У, ) в ^] , ( у ,, ) c = 1[( у ,, ) a + ( у ,, ) в ] •

Составляющие    кинетической энергии,    характеризующие поступательное (Екп) и вращательное (Екv) движение колес и платформы, а также скорости их изменения (Wkn , WKv) для каждого элемента робота определяют уравнения:

колесо А

( E kn ) a = 0,5 m A ( r ^ t ) ² ,        ( E ) a = 0,5 J a (Y_t ) ²

^{( W} kn ) A = m A ⁽ x t x tt + y_ty_tt ) A = ^0,5 m A r²^ t = m A r'YY „ ,

(W kv ) a = 0,5 J a ( Y ) t = J A ^ t ^ tt ,

(Wk )A = (mAr2 + JA Wtt = JpAYtYtt , колесо В

( E kn ) в = 0,5 m ( x t ² + y_t ² ) в = 0,5 m . [ r Y + ( d - b ) ² 0 ² - 2 r ( d - b>_t0_t ] ,

( E kv ) в = 0,5 J b ( ф , ) ,

(Wkn)В = mB (xtxtt+ У ,У tt)В = Жв {r2YYtt + (d - b)2 0t0tt - 2r(d - b)(0ttYt + 0tYtt)}, или x          2r        d b - bx,         2/, d - bx_

• ^{( W} kn ) в = m_B Y Y ^[ Y tt ^- Y tt ^{(1 +} ——^{)] + m} B ^ t ^{r (1 +}-----⁾⁽² Y tt ^- Y tt ) ,

Lr

(Wkv)в = 0,5Jb(ф2)t = JвФtФtt, платформа С

• ^{( E}kn ) С = ^0,5 m e ⁽ x t ^{2 +} y_t ^{2 )} С = ^(1/8) m e ^{{ [ 2(} x t ) A ^{- O} t ⁽ У в ^- У а ) ] ' ^{+[ 2(} y_t ) A ^{+ 0 ( X}B ^{- X}A )Г ^} ,

(Ekn) с = Л me [4( xt2 + yt2) a - Yfr (d - b) + L Of],       (Ekv ) c = 0,5 JO , x 1       2r1         /1 d - b_   1       2r Д d - bx      ,5 dd - bx,

• ^{( W} kn ) c = T ^m c ^ t ^{r [}T Ф tt ^- ¥ tt ⁽T ⁺ —— ^{)] +} T ^m c ^ t ^{r [ -}Ф tt ⁽T ⁺ ——) ⁺ ^ tt ⁽T ^{+ 2}—— ^)]

2       2        2 L      2           2 L        2      L

,

, 2

, 2

W kv ) C = J⁰⁰ = r ? ( ^ t ^- Y t ^)^^ >tt ^- Y tt ) ^JC = r ? J C ^[ ^ t ⁽ Ф« ^- Y tt ) ^- Y t ⁽ Ф« ^- Y tt ^)] .

При движении по прямой ( ф = Y_t ) выполняются соотношения ⁽W> . ) а = Ж а Г 2 YY,, = ( Wh ) в = т в Г 'ФЯ>„ ,   ⁽ W _tn ) C = Ж с Г ²YY „ = Ж с Г ²ФФ>„,

( W kv ) C = 0 .

^{( W} kv ) A = J A ^^ n = ^(W kv ) B = ^J в Ф t Ф tt , Энергетический баланс

W e = M aY, + М в Ф , = ( W kn + W kv ) A + (W„ + W ., ) B + ( W kn + W kv ) C         (14)

должен выполняться при любом соотношении угловых скоростей

• ^We = ^mA^r2 Y Y tt ^{+ m}B^r2 Ф ^[ Ф_и ^- Y tt ^{(1 +} d^b ^{)] + m}B^r2 Y t ^{(1 +} d^b ⁾⁽² Y tt ^- Ф , t ) ⁺

• 1    _{2 r}1        Д d - b„  1    _{2 r Z}1 d - b,     ,5 dd - b„

+ тЩ_сг Ф [- Ф> - Y ,,(- +----- )] + m/n_rr Yt[-Yt (- +----- ) + Y ,,(- + 2-----)] +

CtttttCttttt r2

⁺ J AYtYtt ⁺ J BYYtt ⁺ "J ^jc ⁽ Y t ^- Y t ⁾⁽ Фп ^- Y tt ) .

Обобщенные силы в виде моментов на приводных валах можно найти по уравнениям

• 2          2/, d - b_x_         _х 1      2т /1 d - b_{x       z}5 dd - b_

^M A = ^m A ^r Y tt ^{+ m} B ^{r (1 +} —— ⁾⁽² Y tt ^- Y tt ) ⁺ T ^m c ^{r [ -} Y tt ⁽T ⁺ ——)⁺ Y tt ⁽T ^{+ 2} ——^{)] +}

L             2         2 L       2     L r ,

+ JAV u ^- "J J C ( Фи -Vtt ) ,

2r             , d ^{— b}M ¹ 2г¹          z¹ , d ^{— b} M r . ^{r 2} r            x

M B = m B r [ ф tt ^- V tt ⁽¹ +      ^)] + “ m c^{r [}- P tt ^- V tt (t +      ^)] + ^Jв Ф tt + "J ^JC ( Ф и ^- V tt

L    2     2        l L          L

Проверку расчета проводим по выполнению баланса (14)

M a V. + M в Ф t = ( W kn + W kv ) A + ( W kn + W kv ) B + ( W kn + W kv ) c .

Расчеты проведены для нескольких вариантов изменения углов поворота и угловых скоростей ведущих колес.

Вариант 1:

,     . -   nt            n ,      nt

Ф = A + A sin — , Ф = — A cos — ,

¹    2 T         2 T_x ¹    2 T

„ ,         nt             n .   nt

V = B_n + B , cos--- , v =-- B . sin---

^{0    1}    2 T          2 T₂   ¹    2 T₂

P tt =

V tt

—

n

A2

V ² T 7

.   nt

A sin —

¹    2 T

2     ²

TT

V ^{2 T}2 7

n t cos---- .

2 T 2

Если углы и угловые скорости изменяются пропорционально, например

V = k p , тогда получаем движение «по кругу» (рис. 2) с соотношениями

V t = ^k P_t ,      V tt = ^к Фи ,

П

Ф = A 0 + A jSm — ,

п ,     n t

Ф = —A cos— , ^Y.   2 T ¹    2 T

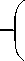
п

2T

A 1

.   nt sin —, 2T

rr     r   r

⁶ t = -⁽ 9 t ^- V t ) = -Ф . ^{(1 - k} ) ,        6 tt = -⁽ 9 tt ^- V tt ) = ^ф^<Ри ^{(1 - k} ) ,

9 = 9 o + - ( ф - V ) = 9 o + - Ф (1 - к ) ,

t

t

u_A ( t ) = x_A - a_A = r j V cos 9 dt = rk j cos

r

— (1 - к^p d p = L

t

t

^va ⁽ . ) = У а ^- P a = ^r j V t ^sin O d = ^rk j ^sin у ^{(1 - k} )> Ф ^d P = ^{- L}

k

1 - k

k

1 - k

^sin -_L^{(1 - k} ) Ф ,

{ ^cos L ^{(1 - k} ) Ф ^- 1 ^ .

При вращении относительно центра масс (рис. 3) моменты и угловые скорости на колесах А и В равны по величине, но противоположны по знаку. Результаты расчетов для более сложных траекторий, а также соотношения моментов на ведущих колесах приведены на рис. 4 и 5.

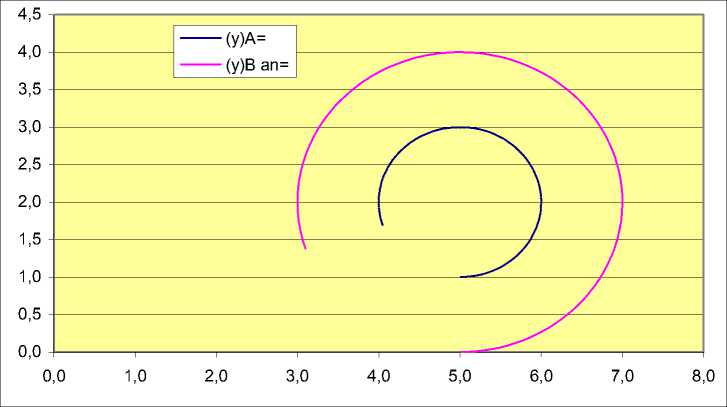
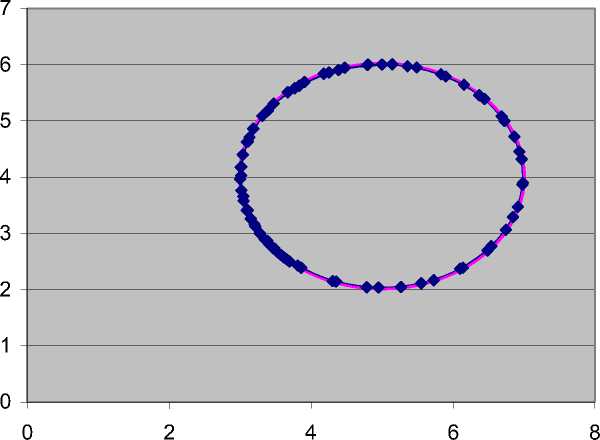
Рис. 2. Движение навигационного робота по кругу

(Y)A= (y)B=

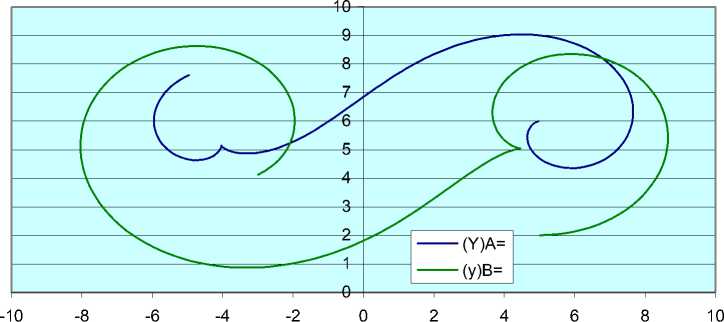
Рис. 3. Вращение навигационного робота относительно центра масс

а)

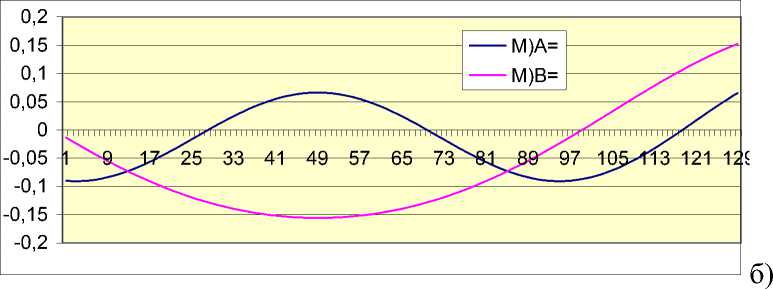
Рис. 4. Движение робота по заданной траектории (а) и соотношения между моментами на ведущих колесах (б)

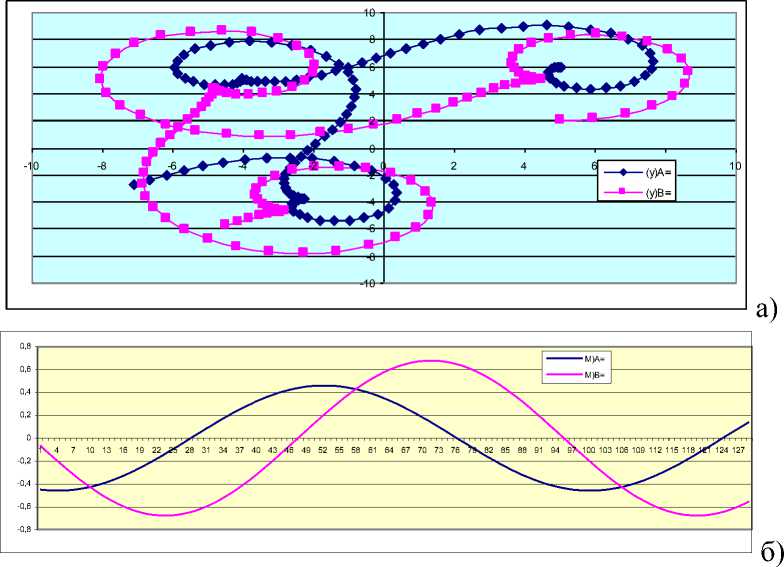
Рис. 5. Траектории точек А и В (а) при соотношении между моментами (б).

Разработанная математическая модель с окончательными зависимостями, записанными через независимые функции угловых скоростей, позволяет определить их по заданной траектории движения робота, а затем найти любые другие кинематические или динамические характеристики, в том числе необходимые для реализации заданного движения мощности, подаваемые на приводы независимых ведущих колес.