Управление формированием рудной базы металлургического предприятия на основе интеграции моделей доменного процесса и разрушения агломерата

В настоящий момент при сравнении полезности рудных материалов, используемых в доменном процессе после их агломерации, как правило, оперируют усредненными эффектами влияния качественных характеристик агломерата на среднюю производительность и расход кокса в доменном процессе [1]. Основными показателями оценки качества агломерата являются индексы: механической холодной прочности TI (Tumble Index согласно ISO 3271); восстановимости RI (Reductive Index согласно ISO 4695); прочности после восстановления RDI (Grounding strength in temperature recovery по ISO 4696 – 1).

На рис. 1 приведены результаты расчетов [2] влияния восстановимости и прочности железорудных материалов на технико-экономические показатели доменной печи №9 «ММК» относительно базового варианта работы печи в 2009 г. Представленные зависимости являются усредненными и не предполагают учета рудной принадлежности материалов, используемых при агломерации.

В работе [3] предложена модель разрушения металлургического агломерата, основанная на комбинированном использовании модели напряженного состояния твердого включения в матрице и модели разрушения на основе закона Риттингера. Определены нагрузки, действующие на куски агломерата в испытательном барабане, и предложен способ адаптации модели – 169 –

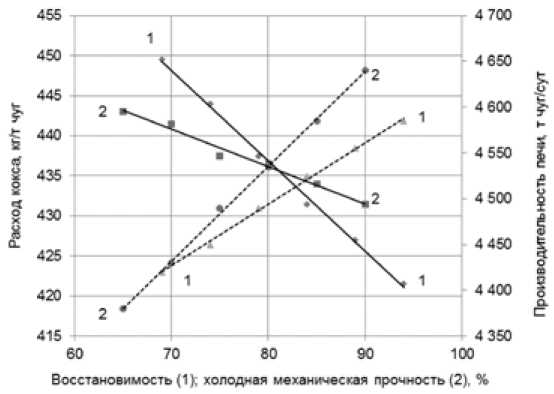
Рис. 1. Рассчитанное в [2] влияние восстановимости (1) и холодной прочности (2) на расход кокса (––) и производительность (- - -) для условий доменной печи №9 ОАО «ММК»

При условии стабильной рудной базы использование усредненных эффектов влияния на эффективность доменного процесса оправданно. В то же время в текущих экономических условиях взаимоотношения с поставщиками рудных материалов могут отличаться нестабильностью [4].

Например, теперь аглофабрики «ММК» получают усредненную смесь из рудных материалов более чем ста различных месторождений и, исходя из ее параметров, выполняют дозирование топлива и известняка, что является основными управляющими воздействиями на качество агломерата. Для уточнения индивидуальных эффектов влияния механической прочности агломератов из различных железорудных материалов на эффективность доменного процесса при формировании рудной базы предприятия необходима интеграция модели разрушения агломерата [3] с моделью доменного процесса.

Интеграция модели разрушения агломератав модель доменного процесса

В доменной печи можно выделить две зоны – косвенного восстановления железа и прямого восстановления. В первой (верхней) зоне большое влияние на перепад давления газов оказывает гранулометрический состав шихты и механическая прочность агломерата. Во второй (нижней) зоне важна горячая прочность компонентов шихты, которая характеризует способ-

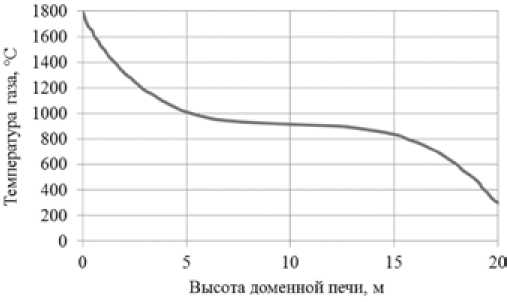
Рис. 2. Принятое допущение о распределении температур по высоте ДП: t =–0,0019 H ⁵ + 0,1085 H ⁴ – – 2,94 H ³ + 41,9 H ² – 299,9 H + 1778, °С

Fig. 2. Accepted assumption concerning the temperature distribution along the blast furnace height: t =–0,0019H5 + 0,1085H4 – 2,94H3 + 41,9H2 – 299,9H + 1778, °С ность материалов сопротивляться нагрузке при высоких температурах. Модель разрушения агломерата [3] ориентирована на верхнюю зону. Поэтому рассмотренный далее расчет учитывает гранулометрический состав в верхней части печи, а для нижней части расчет ведется согласно методике, предложенной в [5].

Модель разрушения [3] определяет статистические вероятностные распределения геометрических и прочностных параметров кусков агломерата, представленных заданным количеством (20 тыс.), разрушение которых по мере движения в шахте доменной печи требуется промоделировать.

Для выполнения приближенных расчетов принято фиксированное распределение температур по высоте доменной печи (ДП) №9 ОАО ММК, изображенное на рис. 2, согласующееся с данными [6, 7]. Принятая высота нижней зоны определяется высотой распара и заплечиков и составляет Hрасп + Hзапл = 5 м, а высота верхней зоны Hш = 15 м при общей рабочей высоте 20 м.

Согласно [8] приняты следующие газодинамические параметры базового режима: избыточное давление дутья 2,5 атм.; избыточное давление на колошнике 1,3 атм.; верхний перепад давления 0,3 атм.; нижний перепад давления 0,9 атм.; общий перепад давления 1,2 атм.; расход горячего дутья 60 м3/с; температура горячего дутья 1200 °С. Согласно [5] зависимость сопротивления слоя шихты в нижней части доменной печи с учетом параметров шихты и дутья для базового варианта доменной плавки выражается уравнением вида низ

низ      ,-,2 ~ 25,

Fд где Аниз – коэффициент потери давления в зоне размягчения, Па∙с2/м6; ΔPниз – нижний перепад давления, Па; Fд – объемный расход горячего дутья, м3/c.

Коэффициент А _низ использовали для упрощенного учета влияния нижней зоны на изменение перепада давления при изменении расхода дутья.

Для описания газодинамических процессов в верхней зоне принято известное уравнение

С. Эгона (S. Ergun) [9]:

w ²

AP = w A

H ^{( 1} - * ш ) T ¹ d_M e Ш 273 ( 1 + P ) ,

где ΔP – перепад давления в слое исследуемого элемента, Па; ψ – коэффициент сопротивления слоя шихты; w – скорость газа через слой шихты, м/с; ρ г – плотность газа (воздуха), кг/м³; ΔH – высота столба (слоя) шихты, м; d _экв.ш – эквивалентный диаметр кусков шихты, м; ε _ш – по-розность шихты, отн. ед.; T – температура газа в исследуемом слое, °С; P – давление газа в исследуемом слое, Па.

Исходя из (2) и ряда работ, где используются схожие выражения [6, 10-12], следует зависимость перепада давления от порозности, эквивалентного диаметра кусков шихты и коэффици- ента сопротивления.

Эквивалентный диаметр может быть рассчитан из ситового состава материалов, по которому определяется свернутый диаметр частиц [10], а порозность – из насыпной и кажущейся плотности материала [13]:

d экв

ⁿ a i

£ di

e = 1 - ^н- = 1 -

У каж

4 m

, nD2^H Y™ каж

где dэкв – эквивалентный диаметр, мм; αi – объемная доля фракции, попавшей в i-ый интервал, отн. ед.; d – середина i-го интервала диаметров кусков, мм; γ , γ – насыпная и кажущаяся н каж плотность материала, кг/м3 (γкаж = 3,34 для агломерата); 4/(π · D2ΔH) – величина, обратная объ ему исследуемого слоя материалов в печи, 1/м3; m – масса материала в объеме слоя, кг.

Порозность агломерата и кокса определяли по зависимостям [11, 13, 14]:

e a = 0,403 • d ОкВ^

_n 0,14

= 0,403 • 1/У ai

, L м d,\

, e _K = 0,222 • d°^2,

где ε – порозность агломерата, отн. ед.; d – эквивалентный диаметр кусков агломерата в а                                                                    экв.а объеме исследуемого элемента, мм; εк – порозность кокса, отн. ед.; dэкв.к – эквивалентный диаметр кусков кокса в объеме исследуемого сегмента, мм.

Очевидно, что при моделировании разрушения материалов в ДП необходимо учитывать разрушение всех компонентов, включая неотъемлемый компонент – кокс, объемная доля которого в шихте значительна. В то же время модель [3] ориентирована на разрушение агломерата. На основании выражения

Mк = MK + O.1441^ Vп°ол24 • «3M-10,                                 (5)

где M ⁰ – исходная массовая доля мелочи в коксе, %; M , M – показатели прочности кокса к                                                                          –10    +25

по ГОСТ 5953-93, %; α 3 – коэффициент учет влияния мелочи, можно найти среднее значение 0

мелочи кокса М _к.ср при ( М _-10= 8,5 % [15, 16]; M _к = 3 %; V _пол = 2014 м³) по высоте верхней зоны доменной печи. Принимая допущение о линейном характере увеличения доли мелочи кокса по высоте шахты, определим долю мелочи в нижней части зоны косвенного восстановления (6), что позволяет рассчитать долю мелочи в любом слое по высоте:

M = 2 • M к.низ             к.ср

-M к.верх,

где M _к.низ – массовая доля мелочи кокса в нижней части зоны косвенного восстановления, %; M к.верх – исходная массовая доля мелочи – 5мм в коксе, %.

Для расчета эквивалентного диаметра кусков кокса в зависимости от доли мелочи выполнили анализ экспериментальных данных работы [15] по распределению крупности кусков кокса на разных ступенях разрушения в барабане Сундгрена (рис. 3 а ), что позволило получить зависимость среднего диаметра кусков кокса от доли мелочи -5мм (рис. 3 б ). Параметры пороз-ности и эквивалентного диаметра окатышей приняты на постоянном уровне.

В доменной печи потоки шихты и газа находятся в противотоке и их встречное движение возможно только при соблюдении определенных условий, одним из которых является ровный сход шихтовых материалов, характеризующийся определенной степенью уравновешивания (СУ) шихты газовым потоком. В работе [5] для расчета СУ предложено выражение

СУ = ^{F г}

F

ш

K ΔP ⋅ S

^ш а γ н

K г Δ P ⋅ S

S ⋅ H а ⋅ γ н^ш

K Δ P г_, ^ш а γ н

где H _a – высота (активного) слоя шихты от уровня воздушных фурм до уровня шихты в печи, м; ш

Δ P – перепад давления газов по высоте активной части, атм.; γ _н – насыпная масса шихты, т/м³;

S – площадь поперечного сечения печи, м²; K _г – параметр адаптации ( ≈ 10).

Наличие информации о размерах кусков материалов в процессе их разрушения позволяет перейти от площади поперечного сечения печи в (7) к эффективной площади (сечения) кусков S Σ в каждом сегменте по высоте верхней части печи:

k ₁      k ₂

S Σ = ∑ ∑ S i , j , S i , j = π ⋅ R i ², j ⋅ N i , j ,                                (8)

i =1 j =1

где S i , j , R i , j , N i , j – эффективная площадь, радиус и число кусков i -й фракции j -го компонента шихты; k ₁, k ₂ – число интервалов размеров кусков и число компонентов шихты.

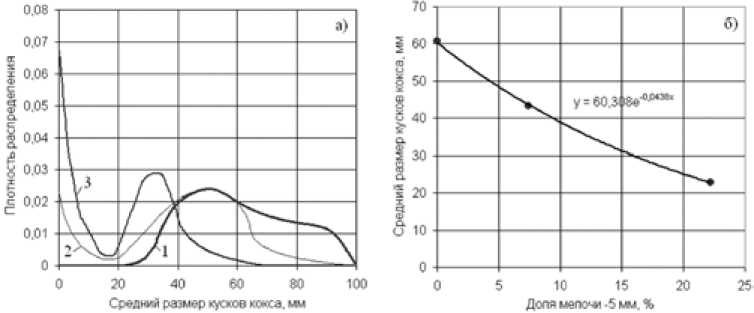
Рис. 3. Распределение крупности кусков кокса на разных ступенях разрушения в барабане Сундгрена (1,2,3 – начало, середина и завершающая стадия испытаний) (а) и рассчитанная зависимость среднего диаметра кусков кокса в зависимости от доли мелочи -5 мм (б)

Fig. 3. а) Distribution of the coke lump size at different fracture stages in a Sundgren drum (1, 2, 3 – beginning, middle and completion test stages); б) calculated dependence of the mean coke lump diameter on the share of smalls – 5 mm

При выполнении настройки модели на базовый режим параметр K _Г упрощенно приняли одинаковым для каждого сегмента по высоте, фракции и компонентам шихты.

Алгоритм расчетов модели газодинамических процессов доменной печи в верхней зоне представлен на рис. 4. На рис. 5 изображена структурная схема взаимодействия параметров блоков модели.

Сложностью используемой схемы расчетов является то, что для первоначального расчета перепадов давления и степеней уравновешивания нет данных о разрушении кусков агломерата и порозности шихты по высоте доменной печи. Поэтому перед началом расчета принимается фиксированная линейная зависимость изменения порозности шихты и эквивалентного диаметра кусков агломерата и кокса по высоте верхней зоны доменной печи.

Расчет перепада давления происходит снизу вверх по слоям. Рассчитываются текущая плотность газового потока ρ gas , его объемный расход F vol.dut и динамическая вязкость μ. По формуле (2) вычисляется перепад давления ∆P в текущем слое высотой ∆H=1м. Для следующего сегмента на высоте давление внизу слоя, с учетом потерь в нижележащем, равно P = P – ∆P, далее производится вычисление перепада давлений с шагом расчета ∆H до верха доменной печи.

Затем рассчитывают степень уравновешивания шихты СУ восходящим потоком газа. При этом слои перебираются напротив сверху вниз для определения силы Q_н давления на материалы текущего слоя верхними слоями, расчета разрушения кусков и определения эквивалентного диаметра кусков агломерата d_экв.а и кокса. Находится новая порозность агломерата ε_а, насыпная плотность агломерата ρ нас.a для каждого слоя и пересчитываются объемные доли компонентов шихты φ_a, φ_k в исследуемом сегменте объемом V_seg.

Расчет повторяется циклически (5-10 циклов) до получения установившегося решения по перепадам давления ∆P по высоте доменной печи и порозности шихты εш.

На рис. 6 показано изменение рассчитанных по модели параметров по высоте верхней части доменной печи №9 ОАО «ММК» для шихты из смеси Соколовского агломерата (49 % по массе), кокса (28 %) и окатышей (23 %) при индексе прочности агломерата TI = 70. Общее среднее значение степени уравновешивания шихты (с учетом СУ нижней зоны) составило 0,56 при коэффициенте K Г = 0,08.

Разработанная модель позволяет оценить влияние принадлежности агломерационного сырья к различным месторождениям на СУ доменного процесса при одинаковом индексе холодной механической прочности. В таблице 1 приведены данные об изменении: СУ; расхода дутья, обеспечивающего СУ = 0,57, стандартное отклонение которого составило 0,96 м3/с, или 1,57 %; производительности и расхода кокса согласно эффектам в [1].

Из данных табл. 1 следует значимое влияние рудной принадлежности агломерационного сырья на производительность доменной печи.

На основе зависимостей настроек модели разрушения агломерата от индекса TI в [3] можно оценить влияние на эффективность доменного процесса изменения механической прочности агломерата в достаточно широком диапазоне. На рис. 7 а видно, что влияние индекса TI на производительность доменной печи неоднозначно и может быть как линейным, так и значимо отличным от линейной зависимости.

На рис. 7 б результаты расчета по изменению производительности доменной печи представлены в форме зависимостей от содержания углерода в агломерационном процессе, полученных – 174 –

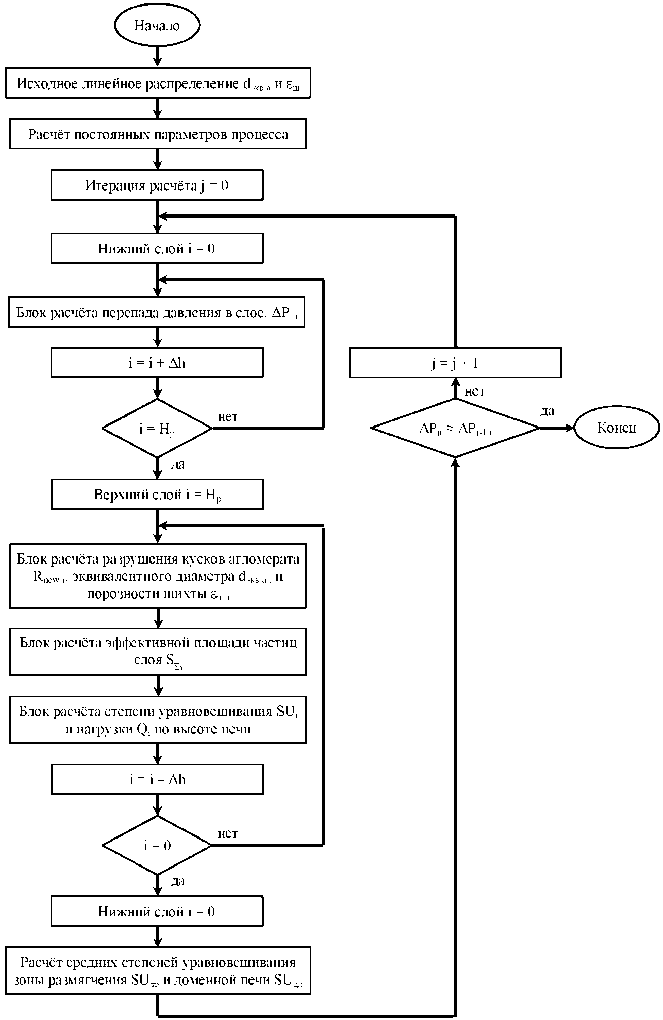
Рис. 4. Алгоритм расчетов модели газодинамических процессов доменной печи в верхней зоне

Fig. 4. Algorithm of model calculations of gas-dynamic processes in the upper zone of the blast furnace

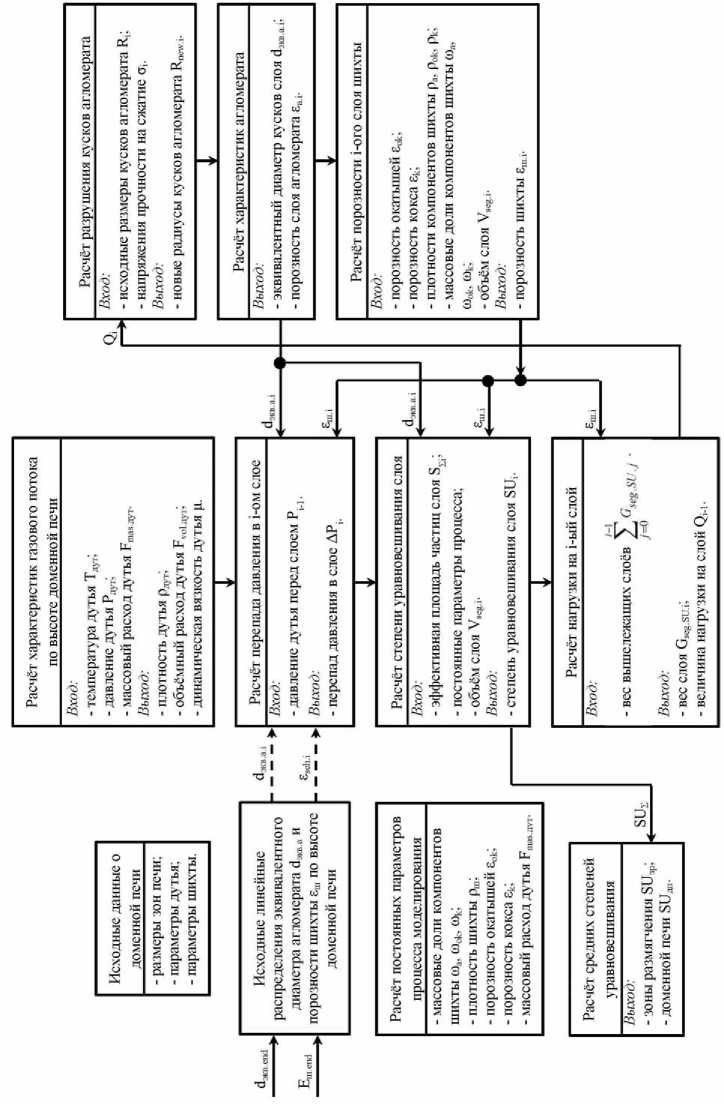
Рис. 5. Структурная схема взаимодействия параметров блоков модели при расчетах

Fig. 5. Structural scheme of the interaction of parameters of model units in calculations

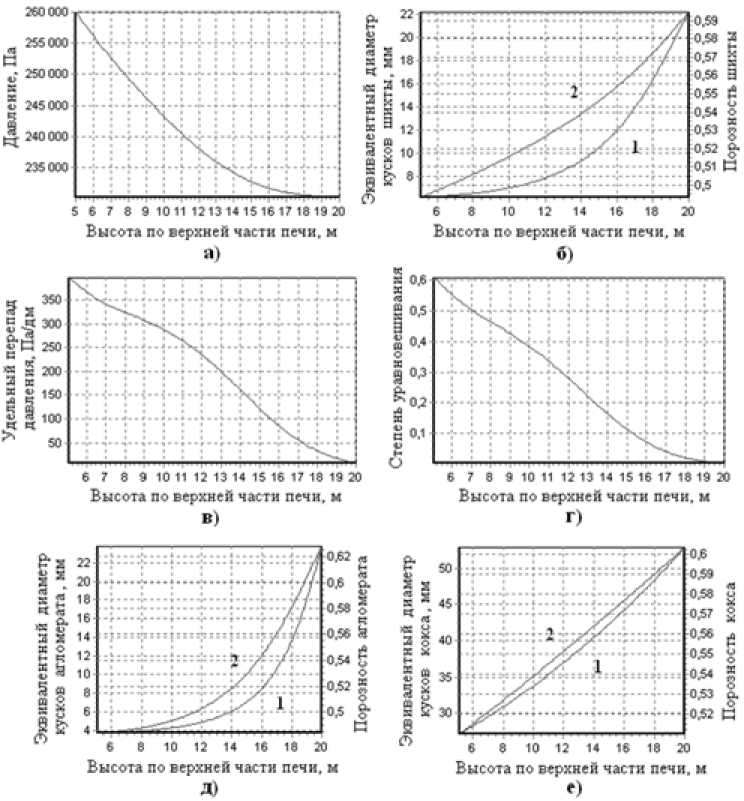
Рис. 6. Изменение рассчитанных по модели параметров по высоте верхней части доменной печи №9 ОАО «ММК» для шихты из смеси Соколовского агломерата (49 % по массе), кокса (28 %) и окатышей (23 %) при индексе прочности агломерата TI = 70: а – давление, Па; б – эквивалентный диаметр кусков шихты, мм; в – удельный перепад давления, Па/дм; г – степень уравновешивания; д-е – эквивалентный диаметр (мм) и порозность агломерата и кокса (1 – диаметр; 2 – порозность)

Fig. 6. Change in parameters calculated as per the model along the height of the upper part of blast furnace No. 9 of OJSC Magnitogorsk Iron & Steel Works for the furnace charge made of mixture of Sokolovskoye agglomerate (49 % by weight), coke (28 %) and pellets (23 %) at agglomerate strength index TI = 70: a) pressure, Pa; б) equivalent diameter of furnace charge lumps, mm; в) specific differential pressure, Pa/dm; г) balance degree; д–е) equivalent diameter (mm) and fractional void volume of the agglomerate and coke (1 – diameter; 2 – fractional void volume)

Таблица 1. Рассчитанное влияние рудной принадлежности агломерационного сырья на показатели доменного процесса при TI = 70 (±0,1)

Table 1. Calculated effect of ore belonging to the agglomeration of feedstock on the values of the blast-furnace process at TI = 70

№	Принадлежность рудных материалов	Основность	СУ	Q д * (м3/с) при СУ = 0,57	Δ П *, %	Δ К *, %
1	Оленегорский концентрат	0,3	0,563	60,40	-0,93	0,044
2		0,75	0,557	60,80	-0,42	0,020
3		1,2	0,558	60,80	-0,42	0,020
4	Высокогорская	0,1	0,524	62,60	1,89	-0,091
5	аглоруда	1,2	0,528	62,41	1,64	-0,079
6	Соколовская	0,1	0,565	60,27	-1,09	0,052
7	аглоруда	1,2	0,560	60,60	-0,67	0,032

Q д , Δ П , Δ К – расход дутья, изменение производительности печи.

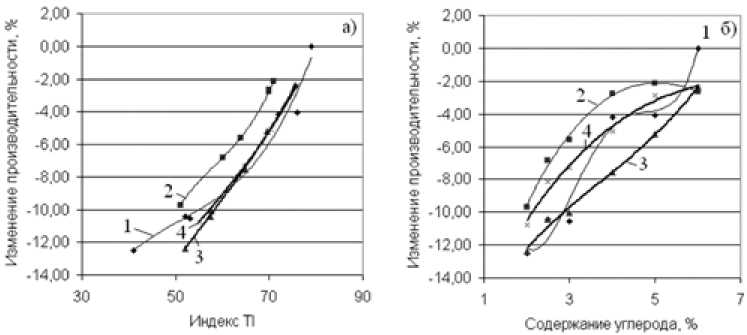
Рис. 7. Рассчитанные зависимости снижения производительности доменной печи от индекса TI (а) и содержания углерода при агломерации (б) по отношению к режиму использования агломерата из Высокогорской руды при TI = 79 для агломератов из: 1 – Высокогорской руды, В = 1,2; 2 – Высокогорской руды, B = 0,1; 3 – Соколовской руды, B = 1,2; 4 – Соколовской руды, B = 0,1

Fig. 7. Calculated dependences of the blast furnace production rate decrease on TI index (a) and carbon content in agglomeration (b) in relation to regime of the agglomerate use from Vysokogorskoye ore at TI = 79 for agglomerates of: 1 – Vysokogorskoye ore, B = 1.2; 2 – Vysokogorskoye ore, B = 0.1; 3 – Sokolovskoye ore, B = 1.2; 4 – Sokolovskoye ore, B = 0.1

с использованием моделей [16, 17]. Из формы зависимостей видно, что при нестабильной сырьевой базе поддержание на постоянном уровне содержания углерода топлива в агломерационной шихте может приводить к значимым колебаниям производительности доменной печи, что снижает стабильность доменного процесса.

Заключение

Основным результатом интеграции моделей доменного процесса и модели разрушения агломерата является возможность решения задач формирования рудной базы предприятия с – 178 – учетом индивидуальной эффективности использования агломератов из различного сырья в доменном процессе, что актуально в условиях непостоянной сырьевой базы.

Из полученных результатов следует относительно слабое влияние непостоянства газодинамических режимов доменной печи на удельный расход кокса в доменном процессе, что объясняется низким значением используемого усредненного коэффициента из работы И.Г. Това-ровского [1], предполагающего изменение удельного расхода кокса 0,2 % на 10 кПа изменения общего перепада давления. Однако нужно учитывать, что рост механической прочности может сопровождаться в отдельных случаях ростом горячей прочности и изменением восстановимости. Учет данных явлений наряду с вероятностными характеристиками распределений показателей качества агломерата позволяет в перспективе повысить эффективность систем управления формированием рудной базы металлургического предприятия и планирования режимов работы доменных печей.