Управление гигантскими всплесками орбитального углового момента структурированных лагерр-гауссовых пучков в среде с общим астигматизмом

Уникальность структурированных вихревых пучков [1 – 14], содержащих множество степеней свободы, заключается не только в их способности переносить огромные массивы данных [1 – 23], в управлении микророботами в оптических пинцетах [24] или в квантовом кодировании сообщений [25], но и в со- противляемости к разрушению своей внутренней структуры при слабых возмущениях, в частности, в турбулентной атмосфере [19–29]. На наш взгляд, такая способность к частичному или полному самовосстановлению структурированных пучков заключается в парадоксальном процессе разрушения единичных пучков Лагерра–Гаусса (ЛГ) под действием несимметричных возмущений. Дело в том, что ЛГ-пучки являются в принципе неустойчивыми структурами из-за их осевой симметрии. Даже слабые несимметричные возмущения способны их превратить в семейство мод Эрмита–Гаусса (ЭГ) [30], число которых равно удвоенному радиальному числу 2n плюс топологический заряд £, т.е. N =2n +£+1. Такое N-кратное вырождение не разрушает структуру исходного ЛГ-пучка до тех пор, пока каждая ЭГ-мода не получает дополнительное независимое фазовое и амплитудное возмущение. Пучок теряет исходную осевую симметрию, но приобретает новые свойства, а именно, каждая ЭГ-мода может переносить независимую информацию, формируя двухпараметрический структурный ЛГ-пучок за счет модуляции амплитуд и фаз собственных ЭГ-мод, как это было показано в наших статьях [31 – 32]. Если в среде достаточно слабые внешние возмущения, не приводящие к возникновению новых мод, то небольшое перераспределение энергии внутри семейства собственных мод не приводит к критическому разрушению структуры сложного пучка.

Фактически формирование структурированного ЛГ-(сЛГ)-пучка из единичной ЛГ-моды связано с разрушением ее осевой симметрии, которое, в свою очередь, выявляет скрытые свойства единичного ЛГ-пучка. Действительно, ЛГ-пучок имеет топологический заряд (ТЗ), равный азимутальному числу £ ЛГ-моды, которое и определяет ее орбитальный угловой момент £ z (ОУМ) [33-35]. Кроме того, радиальное число n не связано с ОУМ и задает только число вырожденных кольцевых дислокаций (темных колец) ЛГ-пучка. Однако возмущение амплитуд и фаз собственных ЭГ-мод в структурированном пучке снимает вырождение по ТЗ в кольцевых дислокациях, которые распадаются на пары оптических вихрей, и изменяют ОУМ структурированного пучка [36–39]. Теперь общее ОУМ пучка формирует 2 n + £ +1 мода [40], а радиальное число n характеризует частоту быстрых осцилляций ОУМ, управляемых амплитудным е и фазовым 9 параметрами структурированного пучка [41]. Однако максимальная амплитуда ОУМ не может превышать величину азимутального числа £ z <  £ в исходном ЛГ-пучке в связи с тем, что новорожденные оптические вихри формируют топологические диполи с равными весами, но разными знаками ТЗ.

Ситуация радикально изменяется, когда структурированный ЛГ-пучок распространяется через среду с простым астигматизмом [42], когда оси астигматической среды ориентированы вдоль осей симметрии структурированного пучка. Симметрия топологических диполей нарушается. В пучке возникают супервсплески ОУМ, максимальная амплитуда которых приблизительно равна половине радиального числа £z« n/2. Тем не менее, при простом астигматизме невозможно задать условия, при которых ОУМ пучка может достигать максимально возможного значения £max _ 2n + £. Потенциальная возможность в расширении области управления как структурой пучка, так и его ОУМ скрывается в еще одной степени свободы, который закладывает в пучок общий астигматизм среды за счет вращения его осей, что позволяет управлять соотношением весов новорожденных оптических вихрей. Таким образом, целью нашей статьи является разработка теории структурированных ЛГ-пучков, постановка эксперимента в средах с общим астигматизмом и выявление эволюции супервсплесков ОУМ с сохранением тонкой структуры сЛГ-пучков, вызванной нарушением их симметрии.

1. Структурные преобразования сЛГ-пучков при общем астигматизме

Задачей этого теоретического параграфа является расчет комплексной амплитуды многопараметрического сЛГ-пучка в среде с общим астигматизмом и анализ его структурных превращений в рамках унитарных преобразований. Начнем с того, что стандартный ЛГ-пучок в базисе ЭГ-мод записывается как

(-1 n 2 n +£

LG n - М = 2Ы " ! Z Я^Р *'- k ''" ‘ ' ( ° ) HG- +—k * ( r ) ,(1)

где P ' ¹ m ' ( • ) – многочлен Якоби,

LG n ,±£ ( r ) = exp ( — r ² ) ( x ± iy ) ^£ L n ( 2 r ² ) , HG n , _m ( r ) = exp ( - r ² ) H n ( V2 x ) H „ ( V2 y )

– комплексные амплитуды ЛГ-и ЭГ-пучков соответственно, r =( x , y ) – безразмерные координаты, нормированные на перетяжку w 0 Гауссова пучка. Ниже мы ограничимся случаем + £ . Каждую ЭГ-моду в (1) можно рассматривать как независимую степень свободы. Чтобы сформировать структурированный пучок, внесем в каждую ЭГ-моду в (1) новую амплитуду е и фазу 9 в соответствии с правилом е _k ( е , 9 ) =1+ е exp ( i k 9 ), так что комплексная амплитуда (1) примет вид структурированного сЛГ-пучка

(-1) n 2 n+£ k sLGn,±£ (r,е, 9)_ 2n+3’ , Z(2i) X 2       n ! k=0

X p n ^{+ £ - k} , n — ^k ) ( ° ) е * ( е , 9 ) HG 2 n +£— * , * ( r ) .

Такой пучок легко сформировать на эксперименте с помощью пространственного модулятора света (SLM) [43–46]. Новое семейство параксиальных структурированных пучков обладает рядом необычных свойств, указанных выше, но что интересно: его комплексную амплитуду (3) можно привести к компактной форме путем длительных преобразований [40] в виде двух стандартных пучков Эрмита–Лагерра–Гаусса (ЭЛГ) [30] с различными управляющими параметрами

(-1)n sLGn ,£ (r, е, 9) = 2+^ { HLGn+£,n (r |Л/4) +         (3)

+ е(-i) n+£ ei(2 n+£)0 HLGn,n+£ (R—^4r |®)}, где © = 9 /2- л /4 - управляющий параметр второго ЭЛГ-пучка,

R

а

cos а sin а

- sin а cos а

a HLG n , m ( • ) -

комплексная амплитуда ЭЛГ-пучка [41]:

HLG _n , m ( r |а ) = 5 i^k cos ⁿ - ^k а sin ^m - ^k ах k =0

х P k⁽ n - ^{k , m} - k ) ( - cos2 а ) HG n + m - k , k ( r ) .

Отсюда следует, что первый член в (3) соотносится с модами ЛГ-в соответствии с преобразованием

HLG n +,. n ( r |п/ 4 ) = ( - 1 ) n 2 ^{n + t} n ! LG „ ., ( r ) , £ >  0.     (5)

Обозначим через ^ и n поперечные координаты пучка в среде с общим астигматизмом, оси которого ориентированы под углом р . Функцию астигматического преобразования среды запишем как

у(р,Р) = (^2 —n2) cos2p + 2^psin2p, (6)

где р = ( ^ , n ). Для комплексной амплитуды (3), записанной в терминах ЭЛГ-пучков, удобно использовать общее астигматическое преобразование в форме Фурье-преобразования [30].

F ' exp ( ib v ( р , Р ) ) sLG n,t ( р , s , 9 ) [ ( r ) =

( — 1 ) n

2 ^{n + t} n !

exp I1

2^1 + b ²     [ 4 ( 1 + b ² ) J

х asLG n ,t ( r , s , 9 , b , P ) , asLG n _{> t} ( r , s , 9 , b , p ) = e ^{i <} < ^{p+n/ 4} ) х

х HLG n+ _t ,n

R -л/4-p ^r 2^1 + b ²

л I            n + £

-to. +s -i х4 I ( )

х е^² n ⁺< ) q e - i z» HLG n , n _{+ <}

f R -у-e r [ 2V1 + b ²

где F ' f ⁽ p y j⁽ r Mv^Lexp ( - i (r, p) ) f ⁽ p ) d ² p

2D Фурье-преобразование, to _— =arctan b , где b - параметр астигматизма. Обозначения углов p , 9 и у раскрыты в формулах А5-А7 в Приложении.

Геометрическая интерпретация ЭЛГ-пучков [30] позволяет представить состояние пучка точкой на сфере единичного радиуса в рамках унитарных преобразований так, что тройка углов ( а , Р , to _- ) характеризует первый и второй члены в (3) и (8), а - задает начальный угол, а углы Р и to _- задают свойства астигматической среды. При распространении через астигматическую среду положение пучка на сфере отслеживает тройка углов ( 9 , p , у ) . Связь между ними позволяет записать комплексную амплитуду в виде выражения (8), а вывод соответствующих выражений

представлен в Приложении А . Возможная геометрическая интерпретация более сложного сЛГ-пучка будет представлена в следующем параграфе.

n=2;t=0        n=2;i=2        n=4;t=3

Рис. 1. Компьютерное моделирование астигматических сЛГ-пучков: (а) интенсивности (инверсия) и (б) фазы для различных квантовых чисел (n; /)

Как мы видим из выражения (8), сЛГ-пучок в астигматической системе характеризуется множеством управляющих параметров, но при проведении эксперимента удобно выбрать часть параметров в виде a = 0, b =1, s =1, изменяя величины квантовых чисел ( n , £ ) и фазовый параметр 9 и угол Р наклона оси астигматизма. Характерные картины интенсивности и фазы представлены на рис. 1 для различных квантовых чисел и угла Р = л /4, в то время как фазовый параметр 9 =0,97 рад выбран в области всплеска ОУМ при простом астигматизме [42].

2. Геометрия астигматических преобразований сЛГ-пучка

Внутренняя симметрия гибридных ЭЛГ-пучков нашла естественное отображение в виде траекторий на поверхности единичной 2D-сферы Пуанкаре в рамках унитарных преобразований [47, 48]. Фактически, такая геометрия подчеркивает внутреннее единство представлений спинового и орбитального углового момента. Эта аналогия находит свое продолжение в интерпретации ЭГ-, ЛГ- и ЭЛГ-мод в виде 2D-осцилляторов в гамильтоновой динамике [49] и представлений в виде лучей на обобщенной сфере Майорана [50].

Однако астигматический сЛГ- (асЛГ)-пучок, содержащий две ЭЛГ-моды с двумя различными управляющими параметрами, теряет свою прежнюю симметрию, а его геометрическое отображение уже требует использования многомерной сферы и, следовательно, теряется простота геометрической интерпретации. С другой стороны, обычный ЭЛГ-пучок характеризуется последовательностью вращений на сфере между начальной и конечной точкой, а промежуточная геометрическая эволюция пучка описывается выражениями (А5)-(А7) для углов 9 ( 9 , Р ) и Р ( 9 , Р ) , как

функций фазового параметра 0 и угла в ориентации осей астигматической среды (цилиндрической линзы). Тогда эволюцию асЛГ-пучка также можно отобразить траекториями на 2D-сфере, не забывая, что такое отображение теряет однозначность. Тем не менее, потеря однозначности восполнится появлением критических точек и траекторий, которые укажут на необходимость детального исследования этих областей. Тогда семейства траекторий для состояний астигматических сЛГ-пучков зададим как

X = sin 2 0 cos ф ,

Y = sin 2 0 sin ф ,                                   (9)

Z = cos 0, так что X2 + Y2 + Z2 =1 для любых углов 0 и р.

На рис. 2 изображены два семейства траекторий, управляемых (а) фазовым параметром 0 при заданных значениях угла Р и (б) углом Р при заданных значениях фазового параметра 0 . Сразу заметим, что эти траектории не отражают эволюцию ОУМ, как это было сделано в статьях [47, 48], но отображают общие свойства астигматических пучков с различными радиальными n и азимутальными £ числами, а также с различными знаками ОУМ. Отчетливо выделяются четыре квадранта, разделенные меридиональными плоскостями (а) XOZ и YOZ , (б) плоскостями, повернутыми на угол п /4 вокруг оси OZ относительно меридиональных плоскостей на рис. 2 а . Все траектории на рис. 2 а,б стягиваются к северному полюсу как для положительных, так и для отрицательных ОУМ при Р^ 0 и 0^ 0. Когда р^±л /2, ± 3 п /2 и 0^±п /2, ± 3 п /2, все траектории стремятся к экватору и к главным меридианам в противоположных квадрантах.

f(P-consl,0)                                     .№,9-cons l)

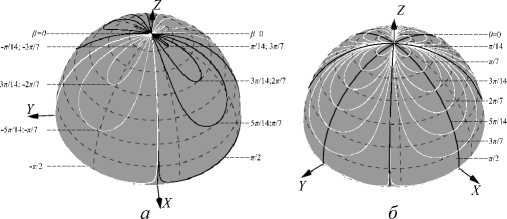
Рис. 2. Теоретически рассчитанные траектории состояний асЛГ-пучка на полусфере единичного радиуса в зависимости от: (а) фазового параметра 0при постоянном угле астигматизма в; (б) угле астигматизма в при постоянном фазовом параметре 0. На полусфере (а) черная кривая соответствует вращению цилиндрической линзы против часовой стрелки, а светлая кривая – по часовой стрелке. На полусфере (б) светлая кривая соответствует изменению угла астигматизма

(- п <  в <  П ), а черные кривые соответствуют главным квадрантам полушарий

Стоит отметить, что вблизи экватора на рис. 2 а траектории слабо зависят от угла р , который задает направление оси астигматизма при изменяющемся

фазовом параметре 0 , но вблизи главных меридианов угол Р меняет знак. Аналогичная ситуация возникает с изменением знака фазового параметра на рис. 2 б . Это указывает на то, что в области этих значений управляющих параметров следует ожидать радикальных изменений в структуре пучков. На первый взгляд кажется, что свойства пучков в соседних квадрантах на рис. 2 а , б должны периодически воспроизводиться.

Однако нарушение исходной симметрии гибридных ЭЛГ-мод может вызвать неожиданные эффекты при вращении астигматической системы по часовой стрелке и против неё как в вырожденной точке северного полюса, так и вблизи главных меридианов, о чем мы поговорим в следующих параграфах.

• 3.    Управление всплесками ОУМ

Расчеты, приведенные в Приложении Б , показывают, что удельный ОУМ многопараметрического пучка после астигматического элемента запишем в виде отношения полного ОУМ к полной интенсивности пучка

£z [ asLG„ .£ ( r , е , 0 , b , р ) ] =

£ ( sin2 a _r -е ² sin 2 a ₂ ) + 2Re [ c * c ₂ • U ]

=       Г+’Ё^+ЁкфГ'сГТ]       , где сГ = е'£(Р+п/4), с2 = е(-i)n+£ ei(2n+£)0e-£Ф;

( n _r, т_Г ) = ( n + £ , n ) ; ( n ₂, m ₂ ) = ( n , n + £ ) ;

a _r =п /4 -го - ; a ₂ =0 ,; го - = arctan b ; у = п /4 -у

U = £ X⁽ „” , ” ^{+ £} ) ( a _r, a ₂, y ) sin2 a _r -- { ( n + £ + r ) X⁽ „” -f^{+ £ )} ( a r , a 2 , y ) + + ( n + 1 ) X n +r " ^{+ £ )} ( a r , a ₂, y ) } cos2 a_b V = X <” ^{, n + £} ) ( a r , a ₂, у ) .

Выясним, какие скрытые свойства асЛГ-пучка с нарушенной симметрией в астигматической среде проявляются при вариации параметров пучка. Действительно, как мы отмечали выше, спектр мод симметричного структурированного пучка сЛГ содержит моды с ± (2 n + £ ) ОУМ. Однако наличие такого широкого спектра мод приводит только к быстрым осцилляциям ОУМ при вариации фазового параметра 0 , в то время как его максимальная величина не может превышать ОУМ £ _z = £ исходного ЛГ-пучка [41]. Ситуация резко изменяется, когда пучок проходит через среду с простым астигматизмом ( Р = 0) и возникают всплески ОУМ, величина которых не превышает половины радиального числа исходной ЛГ-моды £ _z ® n /2 [42], но при £ = 0 ОУМ исчезает ( £ _z = 0).

Детальную картину эволюции ОУМ при вариации параметров 0 и р в асЛГ-пучке иллюстрируют рис. 3

и рис. 4. Нарушение симметрии пучка при общем астигматизме вызывает расщепление вырожденных кольцевых дислокаций и появление новых вихрей, что включает в процесс формирования ОУМ как радиальные, так и азимутальные числа. Результатом этого процесса является появление новых всплесков ОУМ. Мы обнаружили, что амплитуды таких всплесков могут превышать сумму радиального и азимутального числа I™ ^ах >  Пп + /| при ориентации оси астигматизма β = ± π /4. Также наблюдаются мощные всплески ОУМ в окрестности углов β ≈ 0; π , при этом возникает конверсия знака ОУМ при повороте оси астигматизма на угол π /2 относительно исходных углов.

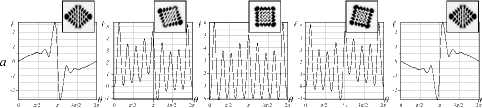
//=0                 ,т/6                 я74                 я/3                 тг/2

Рис. 3. Кривые ОУМ Z z (теория) асЛГ-пучка:

(а) (п = 4; Z=1) и (б) (п = 20; Z=1) в зависимости от фазового параметра θ для различных углов астигматизма β . На выносках представлены распределения интенсивности (эксперимент) для (а) θ ≈ 0,97 π и (б) θ ≈ 0,98 π

Тем не менее, нам пока не удалось найти условия, при которых ОУМ достигает своего потенциально возможного значения I™“ ® |2 п + /| . Мы ожидаем, что более детальные исследования процесса формирования ОУМ на основе разделения чистого вклада от оптических вихрей и за счет разрушения симметрии пучка при астигматизме на основе метода моментов интенсивности [51] позволит приблизить решение этой проблемы. В этом аспекте интерес представляет вопрос возникновения острых всплесков ОУМ в пучках с почти прямоугольной формой картины интенсивности на рис. 4, свойственной безвихревым ЭГ-модам.

• 4.    Эффект следования структуры пучка за осью астигматизма

Как мы отмечали ранее [35], асЛГ-пучки могут распространяться в среде с простым астигматизмом (β =0; π /2) без изменения своей структуры при определенных соотношениях между параметрами пучка и астигматической среды. Однако наши предварительные теоретические и экспериментальные исследования показали отсутствие таких условий для среды с общим астигматизмом (β ≠ 0) – нарушение условия подобия масштабов вдоль осей x и y при фокусировке пучка всегда приводит к разрушению симметрии исходного пучка. Тем не менее, столь жесткое требование к разрушению исходной структуры пучка не распространяется на условия сохранения (или частично- го сохранения) разрушенной структуры пучка при повороте оси астигматизма. Именно эту проблему мы и рассмотрим в этом параграфе. Предпосылки к проявлению такого эффекта следования уже заложены в форме траекторий на сфере на рис. 2. Так, траектории состояний пучка на рис. 2б разделены главными меридианами на четыре квадранта и различаются видом отклика структуры пучка на направление оси астигматизма β. При этом параметр θ(θ,β), ответственный за структуру пучка, почти не изменяется в окрестности фазовых параметров θ = π /4, 3π /4, 5π /4. На эксперименте мы обнаружили, что при определенных значениях параметра θ наблюдается синхронное вращение картины интенсивности вслед за поворотом оси цилиндрической линзы в определенном интервале углов β. Но сразу бросается в глаза, что этот эффект по-разному проявляется при вращении угла β по часовой стрелке и против неё. Это экспериментальное наблюдение заставило нас более пристально вглядеться в физический механизм эффекта.

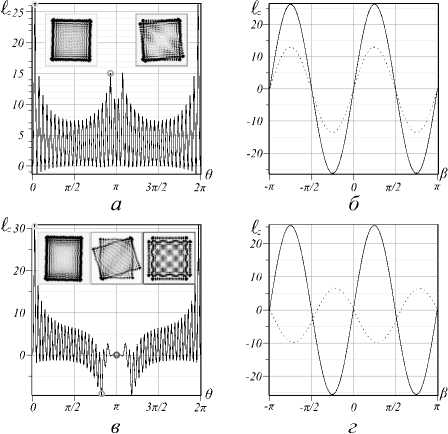
Рис. 4. Кривые ОУМ Z z (теория) асЛГ-пучка: (а, в) в зависимости от фазового параметра θ ; (б,г) в зависимости от параметра астигматизма β ; (а, б) соответствует (п = 20; Z=2) и (в, г) (п = 20; Z=10). Кривая Z z (e) соответствует основным максимумам ОУМ (сплошная кривая) θ = 0,1 π и (пунктирная кривая) θ = π – 0,1. На выносках представлены распределения интенсивности (эксперимент)

При изменении угла β (движение по экватору на рис. 2б) картина интенсивности поворачивается в целом на угол φ, который легко определить из соотношений (8), как ф = arctgY = arctg (tg Ф).

Семейство кривых на рис. 5 соответствует зависимости (13), где угол ф(0,в) задан соотношением (А6) из Приложения А. Мы видим, что светлая кривая для θ = 0,51π имеет почти ступенчатую форму с широкими плато, где положение картины интенсивности не меняется, но затем следует резкий поворот оси картины интенсивности. По мере стремления фазового параметра к θ → π ступенчатая кривая сглаживается (серая кривая), так что в окрестности θ ≈ π наблюдается прямо пропорциональная зависимость φ =– β для черной кривой. Однако зависимости φ (β) на рис. 5 не отражают вида перестройки (или сохранения) структуры картины интенсивности при вращении оси астигматизма. На эксперименте и компьютерном моделировании этот процесс был исследован, а основные результаты представлены на рис. 6.

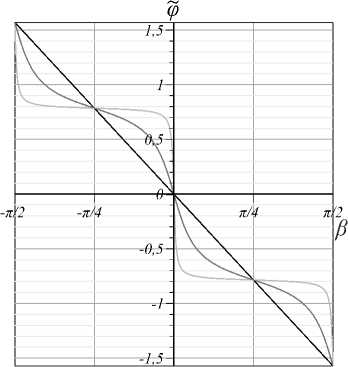
Рис. 5. Теоретическая зависимость угла поворота р ( в ) картины интенсивности на угол β вращения цилиндрической линзы для фазового параметра θ : (светлая кривая) – θ = 0,51 π ; (серая кривая) – θ = 0,6 π ; (черная кривая) – θ = 0,98 π

Наши измерения картины интенсивности и ее структурные перестройки при вращении цилиндрической линзы проводились на экспериментальной установке, подробно описанной в нашей статье [32] (см. рис. 7 в статье [32]). Цилиндрическая линза с фокусным расстоянием f cyl = 15 см крепилась в поворотном устройстве оптического столика, позволяющего устанавливать угол β оси цилиндрической линзы с точностью до четверти углового градуса.

Структурированный ЛГ-пучок формировался на SLM, цифровое обеспечение которого позволяло управлять радиальным п и азимутальным £ числами пучка, его амплитудным ε и фазовым θ параметрами. Картина интенсивности детектировалась в плоскости двойного фокуса z = 2 f cyl цилиндрической линзы с последующей цифровой обработкой.

В верхней части рис. 6 изображены картины интенсивности асЛГ-пучка при заданном направлении β оси астигматизма. Градиент серого на полукруге отображает степень корреляции η структуры пучка относительно исходной картины.

В нижней части полукруга изображен геликоидальный волновой фронт пучка, падающего на ци- линдрическую линзу. Направление закрутки геликоида соответствует знаку ТЗ исходного ЛГ-пучка. Мы обнаружили, что степень сохранения (степень корреляции) структуры пучка при вращении цилиндрической линзы зависит от соотношения между ТЗ пучка и направлением вращения цилиндрической линзы (знаком угла β). Так, если знак угла β совпадает со знаком ТЗ пучка, то структура пучка слабо изменяется в процессе структурного отслеживания оси линзы. В противоположном случае структура пучка быстро разрушается.

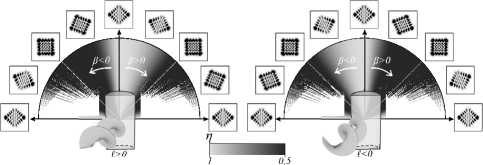
Рис. 6. Моделирование структуры асЛГ-пучка после вращения цилиндрической линзы для (п = 4; I= ± 1). Картина интенсивности (инверсия) повторяет вращение оси цилиндрической линзы для Z>0, в >0 и Z<0, в <0, в то время как при ^>0, в <0 и Z <0, в >0 картина интенсивности быстро изменяется

Мы заинтересовались, как структура пучка будет изменяться при пересечении критической точки для фазового параметра θ =0, π /4, 3 π /4, где наблюдается резкий всплеск ОУМ, в то время как картина интенсивности имеет много общего с картиной интенсивности ЭГ-моды? Ответ на этот вопрос иллюстрирует рис. 7. Первая строка на рис. 7 демонстрирует картины интенсивности асЛГ-пучка для 9 = 0 и £ = 0 при различных направлениях β вращения цилиндрической линзы.

При этом наблюдается четкое отслеживание направления вращения линзы и картины интенсивности без разрушения ее структуры.

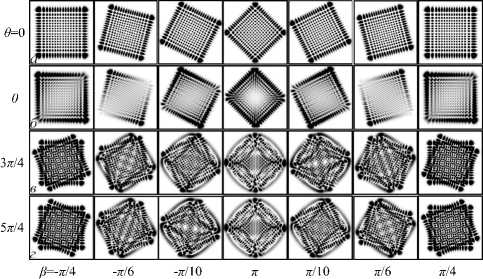
Рис. 7. Компьютерное моделирование интенсивности

(инверсия) асЛГ-пучка для (а, б) (п = 15; 1= 0); (в, г) (п = 15; /= 1) при различных параметрах 9 и в

Однако для ненулевого ТЗ ( / =1) возникает частичное разрушение исходной картины интенсивности для различных знаков ТЗ и β (вторая строка), хотя главные диагонали прямоугольников в картинах интенсивности строго следуют за поворотом цилиндрической линзы.

Ситуация резко изменяется при больших значениях фазового параметра 9 (третья и четвертая строка на рис. 7). Вращение линзы приводит к резкой перестройке картины интенсивности. Особенно ярко это проявляется при смене знака ТЗ пучка (четвертая строка рис. 7). Хотя структура пучка и разрушается при вращении линзы, наблюдается строгая корреляция между картинами при вращении линзы по и против часовой стрелки. В самом деле, сравнение картин интенсивности в третьей и четвертой строках рис. 7 показывает, что их тонкая структура совпадает, если направление вращения цилиндрической линзы изменяется одновременно с изменением знака ОУМ, т.е. произведение ОУМ на знак вращения линзы / _z - sign ( в ) = const должно оставаться неизменным.

Для того чтобы подтвердить или опровергнуть полученные теоретические предсказания, требуется сравнить между собой картины интенсивности для различных фазовых параметров 9 , углов вращения в цилиндрической линзы и / _z ОУМ посредством степени корреляции п , измеренной на эксперименте и представленной на рис. 8.

Кривые для 9 = п на рис. 8 описывают степень корреляции п ( в ) для пучков с нулевым ОУМ ( I _z = 0), они симметрично преобразуют интенсивность при вращении линзы по и против часовой стрелки с ошибкой измерения до 5%. Симметрия кривой П ( в )нарушается для ненулевых значений ОУМ, когда знаки в и / _z могут быть одинаковыми или различными. Важно отметить, что в интервале углов вращения линзы в^е (0, ±п /8) наблюдается эффект следования структуры пучка за осью вращения цилиндрической линзы при выполнении условия / _z - sign ( в ) = const.

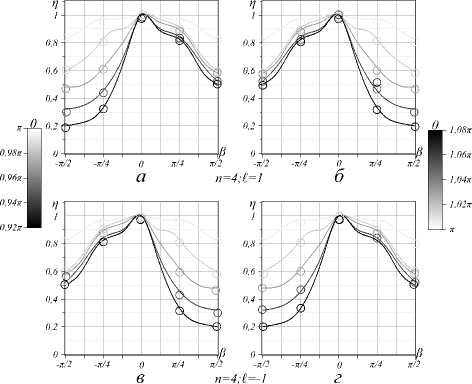
Рис. 8. Кривые степени корреляции (теория) п ( в ) для картин интенсивности в зависимости от угла поворота цилиндрической линзы асЛГ-пучка с положительным и отрицательным ТЗ: (а,б) (п = 4; /= 1) и (в,г) (п = 4; /= -1). Каждая кривая на графике соответствует определённому значению фазового параметра 9 , представленному на рисунке в виде градиента: слева для (а, в), справа для (б, г). Кружки соответствуют экспериментальным точкам.

Выводы

Свойства структурированных ЛГ-пучков в астигматической среде являются ярким примером проявления скрытых свойств стандартных ЛГ- и ЭЛГ-пучков при нарушении их вращательной симметрии. Вращение этих пучков по и против часовой стрелки не изменяет их свойств. Стоит только сложить эти пучки, чтобы получить сЛГ-пучок [40], как свойство вращательной симметрии нарушается и возникают быстрые осцилляции ОУМ, частота которых задается радиальным п числом сЛГ-пучка, в то время как их амплитуда не превышает начального топологического заряда £ (равного азимутальному числу исходной ЛГ-моды). Тем не менее, его спектр мод становится широким, содержащим ОУМ, равный ± (2 п + / ) удвоенному радиальному числу, плюс азимутальное число с противоположными знаками ОУМ.

Мы показали, что в среде с общим астигматизмом ситуация кардинально меняется. Можно выделить две основные особенности. Первой из них является то, что экстремумы ОУМ возникают при угле астигматизма в = п /4 при любых значениях фазового параметра 9 , но их экстремальное значение, превышающее | п + / |, возможно получить только при оптимальных значениях фазового параметра. Второе основное свойство-эффект следования структуры пучка за углом в поворота оси цилиндрической линзы, который проявляется при условии, что произведение ОУМ и знака угла поворота в остается неизменным.

Стоит отметить, что мы рассмотрели только часть из множества скрытых свойств структурированных пучков, утративших вращательную симметрию. Дальнейшие детальные теоретические и экспериментальные исследования заслуживают того, чтобы выявить условия, при которых появляется возможность получить экстремальное ОУМ ± (2 п + / ) путем подавления нежелательных мод.

Работа выполнена при поддержке Российского научного фонда (грант 23-22-00314).