Управление качеством продукции на основе совершенствования методов многомерного статистического контроля процессов

от момента нарушения процесса до момента обнаружения этого нарушения [2].

При контроле многопараметрического процесса многие показатели коррелированны, при этом целесообразно применение многомерных статистических методов. Основные инструменты многомерного контроля – карты Хотеллинга и экспоненциально взвешенных скользящих средних [3].

Применение контрольной карты Хотеллинга предполагает расчет для каждой t- й мгновенной выборки ( t = 1, …, m ) статистики

_T = n(T, -Ц0)TS-1(T, -Ц0),    (1)

где X _t – вектор средних в мгновенных выборках, ц ₀ - вектор целевых средних, 5 -оценка ковариационной матрицы SS. Положение контрольной границы UCL = T kp на заданном уровне значимости при использовании мгновенных выборок определяется формулой:

p ( m - 1)( n - 1) „ ,

T 2=-------------- F 1 -a ⁽ p , mn ^- m ^- p + 1); (2)

kp mn - m - p + 1

где р – количество контролируемых параметров, F _1-a_a( k ₁, k ₂) – квантиль F -распределения Фишера с числами степеней свободы в числителе k ₁, в знаменателе k ₂.

Предположим, что при контроле р показателей многопараметрического процесса Х ₁, Х ₂, …, Х_р имеют место аддитивные постоянные систематические погрешности измерений, заданные вектором С = ( С ₁ С ₂ … С_р )^Т.

Как и для карт Шухарта, эффективность карты Хотеллинга может быть оценена с помощью кривых средней длины серий. Для карты Хотеллинга средняя длина серий вычисляется по формуле:

L ( X ) = —t² -----,       (3)

Tkp

• 1    - J f ( t ; X ) dt

где

^{X 2} = n ⁽ц - ц о ) T !^{- 1} (Ц ^- Ц 0 ) (4) – параметр нецентральности, f(t ;ll ) – плотность нецентрального распределения Хотеллинга.

Обозначим смещение процесса по j -му показателю через Δ _j = µ _j – µ _{0 j} ; тогда с учетом погрешности измерений параметр нецентральности (4) примет вид:

^ 2 = n ( A + C ) T S^{- 1}( A + C ). (5)

Представим систематическую погрешность в виде Сj = сjσj (сj относительная систематическая погрешность по j-му показателю). Задавая различное количество контролируемых параметров, уровни их корреляции, различные объемы выборок n, можно исследовать, как влияют эти факторы на среднюю длину серий L(λ) (3) с учетом соотношения (5) в зависимости от погреш- ностей измерений сj.

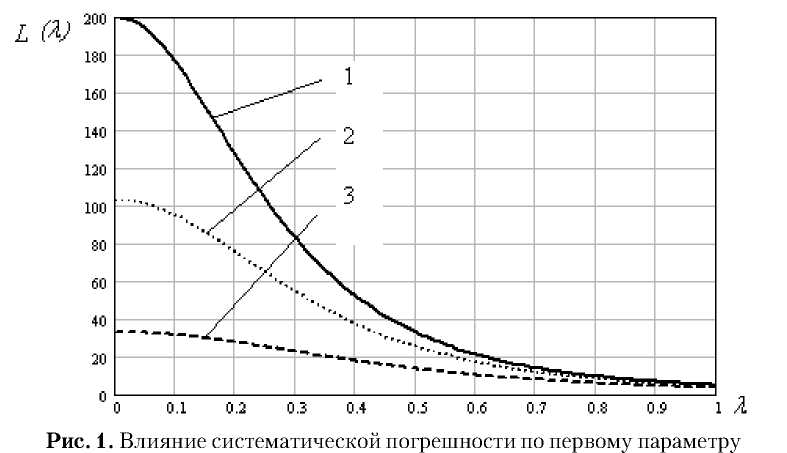
На рис. 1 показаны соответствующие кривые, где принято, что показатели некоррелированны, объем мгновенной выборки n = 5, имеет место систематическая погрешность только по первому показателю (кривая 1 с1 = 0, кривая 2 с1 = 0,25, кривая 3 с1 = 0,5).

Видно, что погрешность наблюдений привела к изменению фактического уровня значимости: если при λ = 0 и отсутствии погрешности с ₁ = 0 возможна в среднем одна ошибка на 200 наблюдений ( L (0) = 200), то при с ₁ = 0,25 L (0) = 103, а при с ₁ = 0,5 L (0) = 33, что недопустимо. Аналогичная картина имеет место при наличии систематических погрешностей по нескольким показателям одновременно [4].

Исследование влияния погрешности измерений на среднюю длину серий в зависимости от объема мгновенной выборки n показало, что уменьшение объема выборки (на рис. 2 с пяти наблюде- ний до одного) существенно ухудшает чувствительность карты как при отсутствии погрешности (что в общем-то очевидно), так и при ее наличии.

на чувствительность карты Хотеллинга

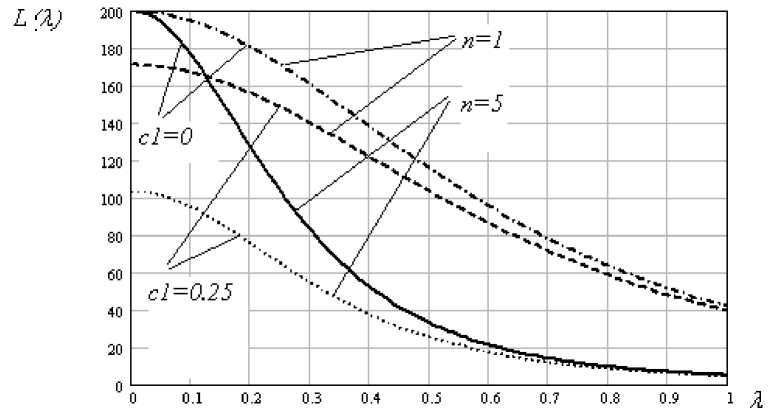
Рис. 2. Влияние систематической погрешности на среднюю длину серий в зависимости от объема мгновенной выборки n

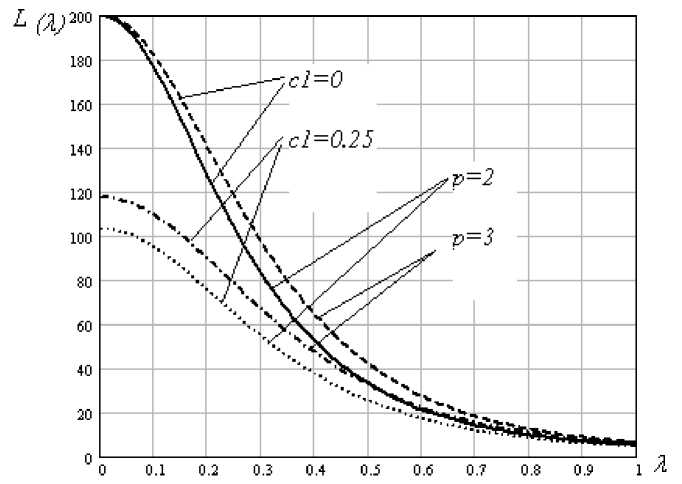
Рис. 3. Влияние систематической погрешности на среднюю длину серий в зависимости от количества контролируемых показателей р

Однако видно, что при индивидуальных наблюдениях ( n = 1) снижение чувствительности карты в зоне λ < 0.3 менее значительно, чем при n = 5. При бо'льших значениях наблюдается обратная картина: при n = 5 и λ > 0.7 кривые с погрешностью измерений и без нее практически совпадают, чего нельзя сказать о кривых для индивидуальных наблюдений.

Влияние погрешности измерений на среднюю длину серий в зависимости от количества контролируемых показателей р иллюстрирует рис. 3: с увеличением количества контролируемых показателей средняя длина серий увеличивается, чувствительность карты Хотеллинга снижается.

Проведенное исследование показало, что наличие систематической погрешности приводит к существенному снижению фактического уровня значимости: вероятность ложной тревоги может возрасти в несколько раз. Отсюда вытекает задача корректировки параметров карты Хотеллинга таким образом, чтобы фактический уровень значимости соответствовал заранее заданному значению α _. Из формулы (3) для расчета средней длины серий при отсутствии смещения среднего уровня процесса L (0) = 1/ α . Используя формулы (3) - (5), необходимо найти такое значение α ₀для расчета положения контрольных границ карты Хотеллинга, которое бы обеспечило заданную вероятность ложной тревоги 1/ α при данном векторе систематических погрешностей. Задача решается численно. Задав диапазон возможных значений α ₀ , используя, например, метод половинного деления, можно найти откорректированное значение уровня значимости.

Теперь предположим, что в процессе измерений имеет место аддитивная случайная погреш- ность, характеризующаяся диагональной матрицей V, элементы которой σvj2 характеризуют случайную погрешность по j-му показателю. Как и ранее, может быть проанализирована эффективность многомерного контроля в зависимости от случайной погрешности измерения в различных условиях.

В качестве примера на рис. 4 показано сравнение эффективности при контроле двух и трех показателей: увеличение числа контролируемых показателей приводит к увеличению средней длины серий как при отсутствии случайной погрешности, так и при ее наличии ( r_j ² = σ _vj ²/ σ ²).

Заметим, что в отличие от систематической погрешности, которая изменяет вероятность ложной тревоги при проведении контроля, случайная погрешность на эту характеристику влияния не оказывает.

Для построения контрольной карты Хотеллинга с учетом систематической и случайной погрешностей вычисляется статистика

T_еt ² = n (( Х _t + С )– µ ₀)^T ( S + V )^-1(( Х _t + С )– µ ₀), (6) при этом положение контрольной границы при использовании для оценивания компонент ковариационной матрицы обучающей выборки определяется формулой:

p ( m - 1)( n - 1)

T 2 = ^F1 -a 0 ⁽ P , mn ^- m ^- P + 1), (7) kp^e mn - m - p + 1

где α ₀ – откорректированное значение уровня значимости.

При мониторинге многопараметрического процесса часто используется карта многомерных экспоненциально взвешенных скользящих средних. Параметр сглаживания и параметр ME_kp , определяющий положение контрольной грани-

L №

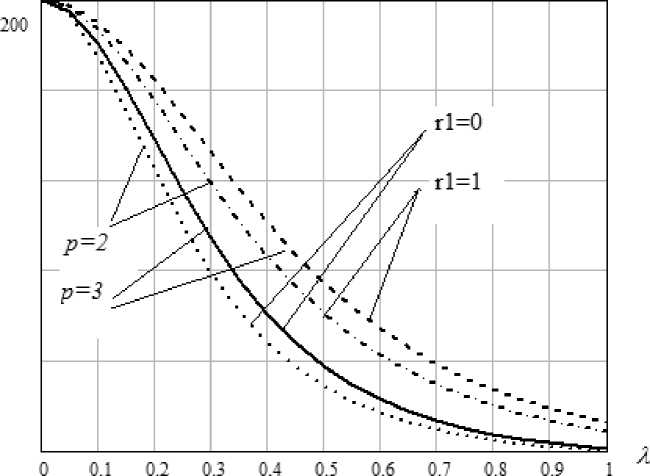
Рис. 4. Зависимость средней длины серий от параметра нецентральности при наличии случайной погрешности при контроле двух и трех показателей качества

цы на карте, а также средняя длина серий карты могут быть определены по результатам статистических испытаний.

Зависимости для расчета многомерных экспоненциально взвешенных скользящих средних с учетом погрешностей измерений примут вид:

Z_еt = (1– k ) Z_{е,t -1}+ k ( Х _t + С – µ ₀), (8) статистика, аналогичная обобщенной статистике Хотеллинга, запишется как

MEеt = Zеt ^T S z е ^-1 Zеt , (9) а оценка ковариационной матрицы Σ _z величин Z_t может быть найдена по формуле

k

5 z е = т—H^{1 —} (1 ^— k ) 2 t ] ( 5 + V) . (10)

• 2    — k

Положение контрольной границы карты экспоненциально взвешенных скользящих средних с учетом погрешностей измерений может быть найдено из регрессионной зависимости

ME_kpе = β ₀ k β^{β 1} p β^{β 2} α ₀ β^{-β 3},         (11)

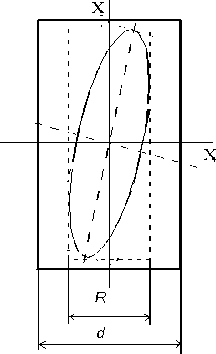
где α ₀ – откорректированный уровень значимости. Контролируемый показатель качества изделия должен находиться в пределах допуска. Для оценки возможности процесса обеспечить выпуск изделия, имеющего показатели качества в пределах допуска, используются индексы воспроизводимости. На рис. 5 показаны возможные состояния двумерного процесса с точки зрения его воспроизводимости, определяющиеся положением и размерами эллипса рассеяния по отношению к прямоугольнику, показывающему границы допуска.

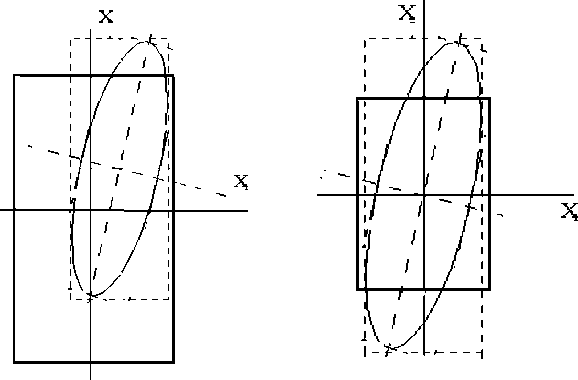
б                         в

Рис. 5. К оценке воспроизводимости многопараметрического процесса:

а – процесс воспроизводим и центрирован; б – процесс нецентрирован; в – процесс невоспроизводим

а

Пусть USL_j и LSL_j – соответственно верхняя и нижняя границы поля допуска для показателя Х_j . Индекс воспроизводимости примет вид:

USL - LSL jj pej ⁼

2j1 TT SI T-2 ,        (12)

j j kpe

n индекс нецентрированности процесса k = 2| j ХД ej USLj -LSLj ,          (13)

где l_j – вектор-столбец из р элементов: нулей во всех строках, кроме j -й, и единицы в j -й строке, T kpe - критическое значение статистики Хотеллинга с учетом откорректированного уровня значимости α ₀, определяющее положение контрольной границы карты (вычисляется по формуле (7)).

Индексы воспроизводимости с учетом нецент-рированности процесса определяются по формуле

С pkej = C pej^ - k^ .       (14)

В качестве примера численного исследования для практического применения разработанных моделей рассмотрена задача о контроле показателей качества клина теплостока.

Для оценки стабильности процесса механической обработки клина теплостока “Redstone” для электронного модуля ЭМ1 в конструктиве “Евро- механика-6U”, предназначенных для работы в герметичных корпусах вычислительной техники специального назначения “Багет” для управления объектами в реальном масштабе времени, контролировались семь показателей – геометрические размеры клина теплостока: Х1 – длина клина 18h12 мм, X2 – угол наклона 45о ± 30', Х3 – высота 7,8–0,2 мм, Х4 – размер 3,9 ± 0,1 мм, Х5 – ширина 7h12 мм, Х6 – размер 3,5 ± 0,1 мм, Х7 – диаметр 5,3h7 мм.

Для предварительного статистического анализа была получена выборка из 50 индивидуальных наблюдений. Анализ данных показал, что значимые корреляции имеют место между показателями Х1 и Х2, Х3 и Х4, Х5 и Х6. Показатель Х7 (диаметр отверстия) не коррелирован ни с одним из других показателей, его контроль проводился с помощью карты Шухарта.

Группы показателей Х1-Х2, Х3-Х4, Х5-Х6 контролировались с использованием трех карт Хотеллинга. Показатель Х2 (угол наклона клина), для которого гипотеза о нормальности распределения отклоняется, был предварительно нормализован с использованием преобразования Джонсона. Систематические и случайные погрешности измерений имеют место по всем семи показателям. Откорректированный уровень значимости составил 0,00395.

Для мониторинга были представлены данные 200 измерений. На рис. 6 показана карта Хотел-

Рисовать в Группу 2

Рисовать в Группу 3

Рисовать с учетом погрешностей

UCL-

UCL = 12,70749

без учета погрешностей

С учетом погрешностей Без учета погрешностей

UCL (с учетом погрешностей)

UCL (без учета погрешностей)

Сохранить расчетные значения Т2

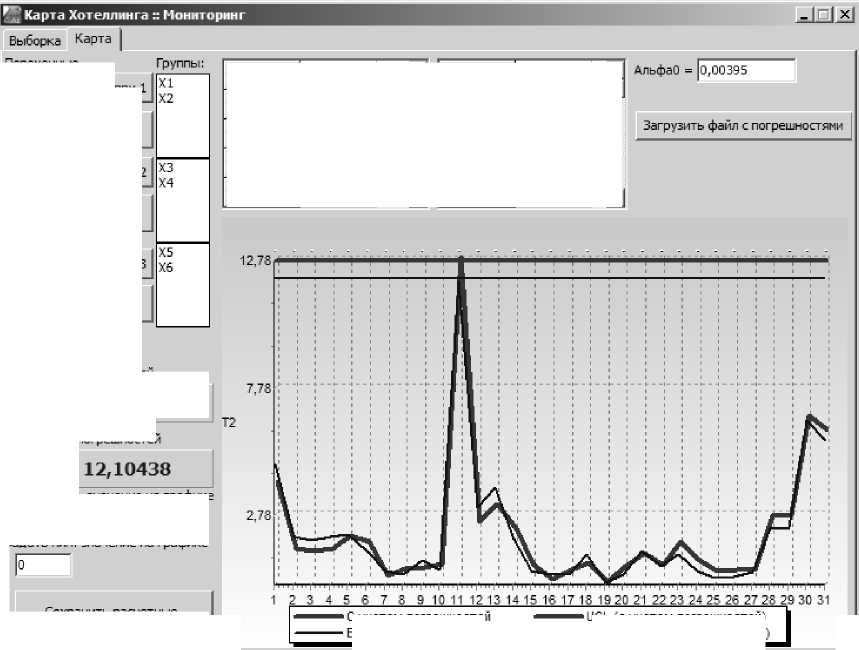
Рис. 6. Карта Хотеллинга при мониторинге процесса обработки клина теплостока: нарушение процесса в 11-ом наблюдении

Переменные

в Группу 1

Задать макс, значение на графике

Задать мин. значение на графике

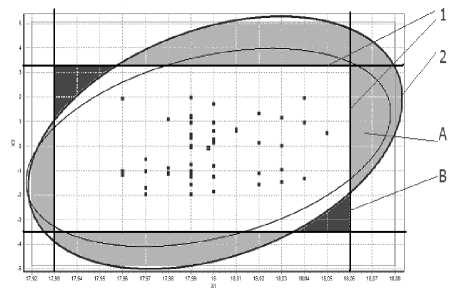
Рис. 7. Сравнение эффективности контроля с учетом погрешностей измерений по картам Шухарта (линии 1) и Хотеллинга (линия 2)

линга для показателей Х1-Х2 при мониторинге процесса (первые 31 измерение), построенная с учетом погрешностей измерений, показавшая нарушение процесса в 11-ом наблюдении.

На рис. 7 проиллюстрировано сравнение рассеяния процесса при контроле с помощью карт Шухарта и Хотеллинга [5]. Здесь Х1 – длина клина, Х2 – нормализованное значение угла наклона. Прямоугольная область, ограниченная линиями 1, соответствует границам карт Шухарта, найденным с учетом погрешностей наблюдений по формулам Х. Миттага: по картам Шухарта точки, лежащие внутри этой области, свидетельствуют о стабильности процесса. Линия 2 показывает эллипс, соответствующий границам карты Хотеллинга (также с учетом систематических и случайных погрешностей). Зона А (светло-серая заливка) – область ложных тревог: карта Шухарта показывает нарушение процесса, но карта Хотеллинга, построенная с учетом кореллирован-ности показателей, свидетельствует об отсутствии нарушений. Зона В (темно-серая заливка), напро- тив, показывает область нарушений процесса, не замеченную картами Шухарта.

Минимальное значение индекса воспроизводимости, найденное по формулам (12) – (14) С_рке = 0,97 имеет показатель Х1 (длина клина), при этом ожидаемый процент несоответствующих единиц продукции равен 0,37%. Без учета погрешностей измерений С_рк = 0,95, процент несоответствующих единиц продукции 0,45%. Доля дефектной продукции за счет учета погрешностей измерений снижается на 22%.

Таким образом, предлагаемая методика многомерного статистического контроля процесса с учетом погрешностей измерений позволяет обеспечить управление качеством выпускаемой продукции путем снижения доли несоответствующих единиц продукции; при этом мониторинг стабильности процесса обеспечивает снижение вероятности ошибок, связанных как с пропуском нарушения в процессе, так и с необоснованной остановкой процесса для регулировки.