Управление космическим роботом при визуальной инспекции состояния геостационарного спутника

ВВЕДЕНИЕ                   ных двигателей (РД) с широтно-импульсной

Информационные спутники на геостационарной орбите (ГСО) имеют потребную длительность службы до 25 лет при наличии технического обслуживания с помощью космических роботов-манипуляторов (КРМ). Статья [1] в этом же выпуске журнала содержат описание системы управления движением (СУД) КРМ для его сближения с целью (геостационарным спутником) от расстояния 5000 м до дальности 50 м, синтезированные алгоритмы наведения и управления, а также результаты анализа динамики СУД при таком сближении. Данная статья продолжает исследования [1] и посвящена проблемам наведения и управления движением КРМ при визуальной инспекции технического состояния цели.

МОДЕЛИ И ПОСТАНОВКА ЗАДАЧИ

В данном режиме в СУД КРМ применяются двигательная установка малой тяги (ДУМТ) на основе восьми термокаталитических реактив-

модуляцией (ШИМ) тяги P m = 0.5 Н каждого РД, силовой гироскопический кластер (СГК) на основе четырёх гиродинов (ГД) с собственным кинетическим моментом (КМ) h g = 30 Нмс и при дальности менее 500 м координаты пространственного движения КРМ относительно цели определяются БИНС, корректируемой сигналами спутников ГЛОНАСС/GPS, и бортовыми оптико-электронными приборами. Для описания движения КРМ применяются геоцентрическая I _е ( O _@ X i Y i Z i ) и солнечно-эклиптическая I s инерциальные системы координат (ИСК), обозначения { • } = col0, [ • ] = line( - ), ( • )^t ,[ -x ] и ° ,~ для векторов, матриц и кватернионов, а также матрицы [ a ] i элементарного поворота вокруг i -ой оси на угол a , i = 1,2,3 = 1 ^ 3 . Используются орбитальные системы координат (ОСК) O_r x ^o y ^o z ^o КРМ с полюсом O_r и цели O _t x_t ^o y_t ^o z_t ^o с полюсом O_t , а также связанная с корпусом КРМ система координат (ССК) O _rxyz . Предполагается, что на борту КРМ имеется телескоп, ось визирования которого параллельна оси O _ry ССК робота, рис. 1 a .

Если считать КРМ твёрдым телом с массой m и тензором инерции J , то упрощённая модель его пространственного движения относительно ИСК в проекции на оси ССК имеет вид

r * + to x r = v ; m ( v * + tox v ) = P ^e + F d ;

Л = Л ° го/2; J to + tox G = Mg + Me + Td.

Здесь кватернион ^Л представляет ориентацию КРМ в ИСК, вектор G = J to + H , где H – вектор КМ СГК; векторы P ^e и M ^e представляют тягу и момент ДУМТ, M ^g = - H * - момент

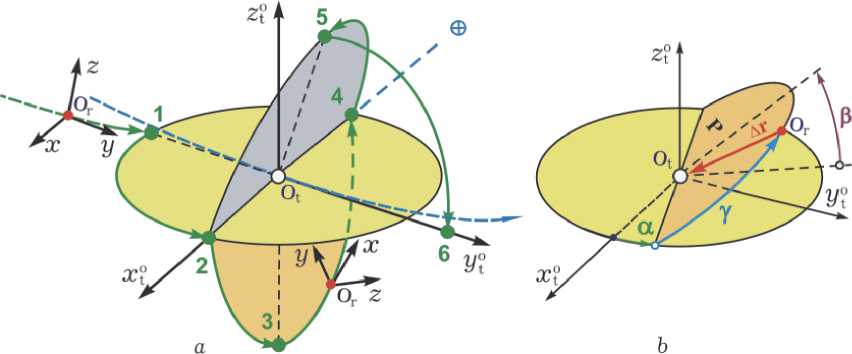
Рис. 1. Схема перелётов КРМ при визуальной инспекции состояния геостационарного спутника

СГК, а F ^d и T ^d - векторы внешних возмущающих сил и моментов и используется символ ( ■ ) * локальной производной по времени.

Расположение цели в ССК робота определяется вектором A r ( t ) = r t ( t ) — r _r ( t ), см. рис. 1 b , а разность их скоростей - вектором A v ( t ) = v _t ( t ) - v r ( t ) . При законе углового наведения робота, заданного кватернионом Л p ( t ) , погрешность ориентации его ССК O_r xyz определяется кватернионом Е = ( e ₀, е ) = Л ^p ° Л при e = { e i } , которому соответствуют матрица ошибки ориентации C ^e = I 3 - 2[ e x ] Q ^ , где Q _e = I 3 e ₀ + [ e x ] , вектор модифицированных параметров Родрига (МПР) о ^е = { о ■ } = е / (1 + e ₀) = е ^etg( ф 74) с ортом e ^e оси Эйлера и углом Ф ^e собственного поворота, а также вектор угловой погрешности 5ф={5ф , }={4 о ; } .

Применяемые дискретные алгоритмы широтно-импульсного управления траекторным движением КРМ и цифрового управления его ориентацией подробно представлены в [1]. В данной статье решаются две задачи: 1) синтез законов наведения КРМ для инспекционного облёта геостационарного спутника с последовательным наблюдением его состояния из шести точек с заданных расстояний, рис. 1 a ; 2) анализ динамики СУД робота при таком облёте.

ЗАКОНЫ НАВЕДЕНИЯ РОБОТА

В ОСК цели траекторные перемещения КРМ между инспекционными наблюдениями спутника удобно задавать плоскостью P, положение которой назначается фиксированными углами а и р на рис. 1 b, и расположением полюса Or КРМ в этой плоскости, которое определяется углом у(t) и модулем 5(t) = Ar(t) вектора s(t) = —Ar(t), см. рис. 1 b. Задача пространственного наведения КРМ состоит в программ- ном расположении sp (t) = —Arp (t) полюса Or КРМ в плоскости P ОСК цели и в программной ориентации оси Ory по орту вектора Arp, когда ось Orz ССК робота направлена по нормали к плоскости перемещения его полюса Or.

Пусть номер j = 1 ^ 5 перелёта (перехода) между точками инспекции соответствует точке завершения предыдущего наблюдения, см. рис. 1 a . При j -ом перелёте КРМ заданной длительности T j вектор его расположения s p ( t ) определяется Углом у p ( t ) в плоскости, заданной углами а j и в j , и расстоянием s j ( t ) от цели. Угол у ^p ( t ) изменяется от начального у pj = у ^p ( t ₁ j ) до конечного у ^p _tj =у ^р ( t ₁ j + T j ) значения, а расстояние s j ( t ) - от начального значения s ^pj = s j ( t ₁ j ) до конечного s fj = s j ( t ₁ j + T j ) . При таком перелёте столбец s ^p _j ( t ) координат центра масс КРМ определяется в ОСК O _tx_t⁰y_t⁰z_t⁰ цели с помощью ортогональной матрицы q , = («мм p ( t )$ .

При краевых условиях pp p p p p

^Y i j ’ ^Y f j ’ ^{Y 1} j = ^{Y 1} j = ⁰ ’ ^{Y f} j = ^{Y f} j = ⁰ ’ pppp p p

• ⁵ i j ’ ^s f j ’ ^s i j ^s i j ’ ⁵ f j ⁵ f j

назначаются сплайны у p ( t ) и s j ( t ) с заданными ограничениями на модули первых и вторых производных по времени, что позволяет по явным соотношениям вычислить векторы программных поступательных перемещений, скоростей и ускорений КРМ относительно ОСК цели.

Эти векторы сначала представляются в ИСК, к ним добавляются соответствующие кинематические параметры движения цели и также по явным соотношениям вычисляются векторы расположения, скорости и ускорения КРМ в ИСК. Наконец, с помощью стандартного кинематического преобразования искомые законы наведения робота в его траекторном движении представляются в ССК Orxyz в виде программных векторов расположения Ar p (t) =-sp (t), скорости Av p = {Avp} и ускорения wp = {wp}. Далее аналогично [1] вычисляются разности между расположениями цели и КРМ Ar(t) = rt (t) — гr (t), их скоростями   Av(t) = vt (t) - vr (t)   и разности p  pp  p  pp

^{A r (} t ⁾ = ^r t ⁽ t ⁾ - ^r r ⁽ t ^{), A V (} t ⁾ = ^V t ⁽ t ⁾ - ^V r ⁽ t ⁾ • а также вектор дискретного рассогласования δ Δ r _s = Δ r _s ^p - Δ r _s между программной разностью A r S = A r p ( t_s ) и измеренной разностью A r s = A r ( t_s ) с периодом T в моменты времени t_s , s e N₀. Аналогичный приём с применением векторных сплайнов используется при синтезе программных изменений кватерниона Л p ( t ) , векторов угловой скорости to ^p = { to ^p } и углового ускорения е ^p = { s p } робота, а также при формировании вектора угловой погрешности δ φ _k .

Пусть на интервале времени t ∈ [14468,24268]с необходимо выполнить инспекцию технического состояния геостационарного спутника на основе наблюдений из шести точек, заданных в окрестности цели. На рис. 2 представлена пространственная программная траектория требуемых перелётов КРМ в ОСК цели, полученная в компьютерной среде MatLab. Временная диаграмма перелётов и наблюдений КРМ приведена на рис. 3, где переходы КРМ между шестью точками наблюдения отмечены синим цветом, а участки наблюдения, где КРМ стабилизируется в ОСК цели, выделены зеленым цветом. В верхней части диаграммы указано текущее время, а в нижней части – длительности наблюдений и перелётов. Здесь длительность j -го перелёта принята одинаковой Tj = 1600 с V j = 1 ^ 5, также как и длительность 300 с (5 минут) наблюдения геостационарного спутника из каждой точки, см. рис. 1 a и 2. Заданные кинематические параметры перелётов КРМ при инспекции состояния спутника приведены в табл. 1.

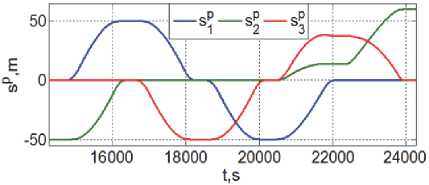
Рис. 4. Программные координаты КРМ в ОСК цели

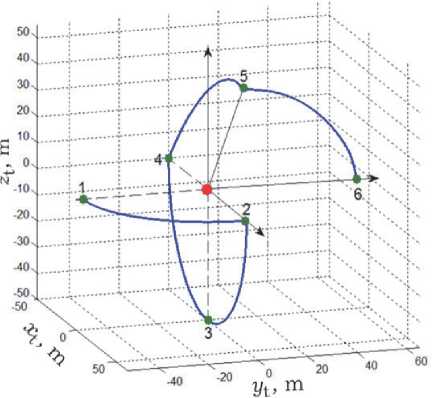
Рис. 2. Траектория перемещения КРМ в ОСК цели

14468       14768          16368       16668          18268

| наблюдение 1 | переход 1-2 ] наблюдение 2 ] переход 2-3

300          1600          300          1600

18268       18568       20168          20468          22066

I наблюдение 3 I переход 3-4 I наблюдение 41 переход 4-5

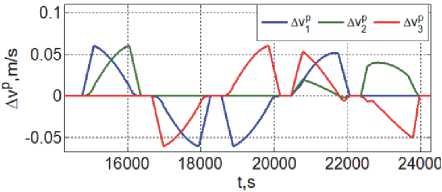
Рис. 5. Скорости КРМ относительно ОСК цели

22068       22368          23968       24268

• ] наблюдение 5[ переход 5-6 I наблюдение 6 I

Рис. 3. Временная диаграмма требуемых перелетов

КРМ и наблюдений состояния спутника

10000   18000   20000   22000   24000

t,S

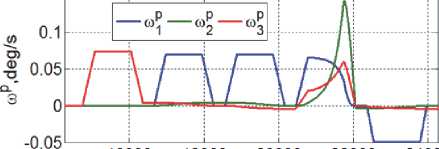
Рис. 6. Программные угловые скорости КРМ

Таблица 1. Параметры перелётов космического робота при инспекции состояния цели

j , #перелета	α j , град	β j , град	Y p -град	Y p - град	sf , м	s f , м
1	0	0	- 90	0	50	50
2	0	- 90	0	90	50	50
3	0	- 90	90	180	50	50
4	0	70	180	90	50	40
5	90	90	70	0	40	60

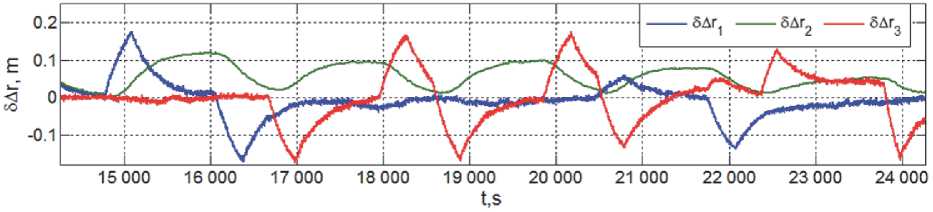
Рис. 7. Погрешности реализации позиционного наведения КРМ при инспекции состояния цели

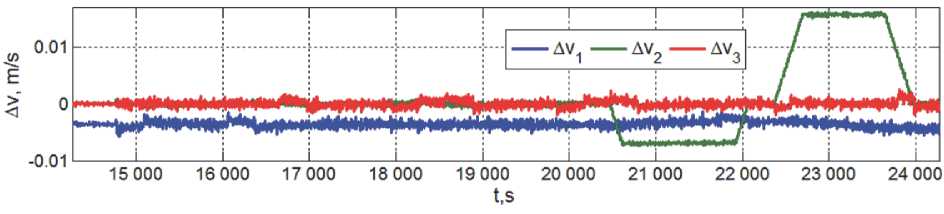
Рис. 8. Погрешности реализации закона наведения КРМ по скорости поступательного движения

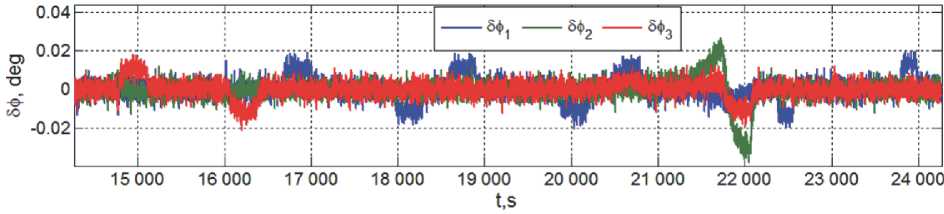
Рис. 9. Погрешности реализации углового наведения КРМ при инспекции состояния цели

На рис. 4 – 6 представлены некоторые результаты автономного расчета на борту КРМ законов его пространственного наведения, полученные по указанным исходным данным. Здесь и далее цветом выделены изменения переменных по рысканию (синий, ось x ), крену (зеленый, ось y ) и тангажу (красный цвет, ось z ).

ДИНАМИКА СИСТЕМЫ УПРАВЛЕНИЯДВИЖЕНИЕМ ПРИ ИНСПЕКЦИИ ЦЕЛИ

При компьютерной имитации нелинейных процессов управления движением робота с массой m = 3000 кг и тензором инерции J = diag(3248, 2348, 3640) кгм² с учетом шумов измерений и внешних возмущений применялись период ШИМ тяги РД в составе ДУМТ T ^e = 4 с при запаздывании T U = 0.25 с и u период цифрового управления ГД в составе СГК T u = 0.25 с. На рис. 7 – 9 представлены некоторые результаты, демонстрирующие показатели точности СУД в процессе визуальной инспекции.

ЗАКЛЮЧЕНИЕ

Кратко представлены методы наведения и управления пространственным движением космического робота в процессе облёта геостационарного спутника при инспекции его состояния, а также численные результаты по эффективности созданных алгоритмов. Здесь следует выделить оригинальный приём параметризации перелётов робота между точками визуальной инспекции, который используется при синтезе законов наведения, и простые робастные алгоритмы управления движением робота, обеспечивающие требуемые показатели позиционной и угловой точности при выполнении инспекции.