Управление микропотоками вещества в канале микрофлюидного чипа с помощью регулируемых тепловых полей

Основными способами управления процессом анализа на микрофлюидном чипе можно считать: 1) выбор топологии (геометрии) микроканала, включая введение специальных смесителей, искривлений, вариаций формы и размеров сечения, многоканальности и т.д.; 2) подбор управляющих напряжений для задания продольного (аксиального) электрического поля; 3) введение микрореакторов, датчиков и организация регистрации продукта, обладающего как большей чувствительностью при детектировании, так и другими физикохимическими характеристиками (подвижностью, коэффициентом диффузии) по сравнению с исходным компонентом; 4) управление состоянием поверхности микроканала (задание величины дзета-потенциала); 5) создание управляемого температурного поля.

Перечисленные выше способы к настоящему времени в разной степени изучены и распространены. В частности, нами были исследованы как экспериментально, так и методами математического моделирования первые два и в меньшей степени — четвертый способ [1-3]. При этом очевидный вывод исследования состоял в том, что усложнение топологии (переменность сечения канала, искривление, ввод промежуточных резервуаров и т.д.), с одной стороны, и модификация алгоритмов формирования управляющих потенциалов, с другой стороны, приводят к удорожанию микрочипа (повышается себестоимость изготовления) и программно-математического обеспечения (ПМО), а также сохраняет требования к высокой квалификации обслуживающего персонала. По аналогичным причинам, практическая реализация способа управления микропотоками пробы с помощью внедренного микрореактора также пред- ставляется затруднительной.

Анализ возможностей применения температурного поля для управления процессом разделения компонентов анализируемой пробы при реализации электрофореза на микрофлюидном чипе является предметом данной работы.

ОСОБЕННОСТИ ОБЪЕКТА ИССЛЕДОВАНИЯ И БАЗОВЫЕ ПОЛОЖЕНИЯ

В работе [2] была промоделирована зависимость центра тяжести и дисперсии пика компонента анализируемой смеси от управляющих параметров разделения смеси: а) напряженности продольного электрического поля — величин управляющих потенциалов (определяющих электрофоретическую и электроосмотическую подвижность); б) физико-химических характеристик анализируемых компонентов (коэффициента диффузии); в) величины дзета-потенциала поверхности канала, определяющего толщину двойного электрического слоя и степень клиновидности конвективного скоростного профиля микропотоков компонентов смеси; г) габаритов микроканала и формы его сечения, поскольку зависимости используют нормированные на ширину микроканала параметры, а время анализа определяется рабочей длиной (длиной до точки детектирования).

Отметим, что выбранная нами ранее топология микрофлюидного чипа, в частности по размерам микроканала, несколько отличается от используемой другими исследователями. В целом, общая геометрическая схема совпадает: длинный тонкий канал с пробой в виде короткой "пробки" [4-6]. При этом исходное распределение вещества в "пробке" аппроксимируется дельта-функцией [5] или, как в [6], либо гауссовым, либо равномерным

(ограниченным длиной) распределением; сечение канала, как правило, круглое, или рассматривается планарная модель. Значительно реже анализируются сечения иной формы [5] (эллиптическое, треугольное или прямоугольное).

В рассматриваемом нами случае речь идет о сечении трапециидальном: средняя полуширина порядка 20-70 мкм, глубина 10-20 мкм (но не превышающая полуширины) и менее, угол наклона стенок 45-60 град. В [5] параметры сечения достаточно близки: глубина прямоугольного канала 20 мкм, ширина 200 мкм, длина — несколько сантиметров. Только в [7] размер канала и исследуемый режим весьма схожи с нашими (ширина канала 50 мкм, средняя скорость конвективного движения около 1 мм/с).

Предлагаемые в большинстве работ теоретические предпосылки (уравнение Навье—Стокса, система уравнений Пуассона—Больцмана для распределения электрического потенциала по сечению микроканала, гипотеза ламинарности конвективного потока) не вызывают несогласия и приняты как базовые и в нашей работе. Исключение составляет гипотеза параболического скоростного профиля аксиальной (маршевой) составляющей конвективной скорости. Ее применяют не только в случае ввода вещества давлением [7, 9], но и при электрокинетическом вводе пробы [5, 6, 8-10], а также для достаточно сложного случая параболического потока после смешивания [11], что представляется малообоснованным, несмотря на весьма широкое ее признание.

Следовательно, при анализе явлений мы основываемся на базовых теоретических предпосылках, большинство из которых получили к настоящему времени практически всеобщее признание среди специалистов по микрофлюидике. Вместе с тем некоторые из них не только носят дискуссионный характер, но и практически опровергнуты нами ранее [2]. К последним относится гипотеза о форме конвективного скоростного профиля.

До недавнего времени в литературе практически отсутствовал количественный анализ влияния температурного поля и состояния поверхности канала на процессы конвективно-диффузионного массопереноса в микроканале чипа при констатации на качественном уровне значимости указанных эффектов. Например, в работе [4] обсуждено влияние джоулева тепла на дисперсию пробы и приведены оценки коэффициентов теплопроводности и теплоемкости материалов, из которых часто изготавливаются чипы (ПДМС, ПММА, ПК, стекло), а также рассмотрено распределение температуры по сечению широкого микроканала ( h = 500 мкм). В лекциях [5] влияние температуры исследовано только с позиций изменения коэффициента динамической вязкости.

В последнее время появились работы [12-15], в которых экспериментально и методом численного моделирования изучены закономерности формирования продольных и поперечных тепловых полей и их влияние на процессы конвективнодиффузионного массопереноса. Тем самым независимо от нас рассмотрены предпосылки для осуществления способа температурного управления процессом разделения смесей при реализации электрофореза в микрочипе.

СПОСОБ ТЕМПЕРАТУРНОГО УПРАВЛЕНИЯ МАССОПЕРЕНОСОМ В МИКРОКАНАЛЕ ЧИПА

Влияние температуры на процесс разделения компонентов смеси может быть описано в рамках общей схемы: 1) изменение толщины двойного электрического слоя (через диэлектрическую проницаемость и саму величину температуры в уравнении Пуассона—Больцмана) ^ 2) изменение клиновидности конвективного скоростного профиля и одновременно изменение коэффициента диффузии всех компонентов смеси ^ 3) изменение интегральных параметров (центра тяжести, дисперсии, асимметрии и т.д.) аналитических пиков.

Толщина двойного электрического слоя к определяется на основе системы уравнений Пуассона—Больцмана [15] равенством k = 2 CN а ZV e e

] e 0 e (T ) к _b T ’

в которое входят характеристики вещества и буфера ( С — концентрация буфера, Zv — валентность частиц), универсальные постоянные ( е — заряд электрона, N j — число Авогадро, к _b — постоянная Больцмана, e 0 — универсальная электрическая константа) и, наконец, характеристики, определяемые тепловым полем ( Т — абсолютная температура, е ( Т) — температурно зависимая величина диэлектрической проницаемости буфера).

Важная особенность, позволяющая без осложнений реализовать указанную схему "чисто температурного управления" процессом разделения компонентов смеси, состоит в том, что в определенных условиях (малости дзета-потенциалов) состояние поверхности микроканала не оказывает влияния на форму скоростного профиля (т.е. "отключается" действие четвертого способа управления — модификацией поверхности). Для этого необходимо выполнение условий корректности линейных аппроксимаций всех уравнений системы Пуассона—Больцмана, в частности в = = ( F £ ₀)/( RT ) <<  1, где F и R — постоянная Фарадея и универсальная газовая постоянная.

Например, при концентрации буфера ( С ₀)

10 ^–5 М, полуширине канала ( h ) 35 мкм, комнатной температуре ( Т =295 К), е =80 критическая (максимальная) величина дзета-потенциала составляет около 27 мВ. (Меньшие величины входят в своеобразную зону нечувствительности, и их варьирование не меняет клиновидности скоростного профиля .) Заметим, что, не изменяя степени кли-новидности профиля m , варьирование величины дзета-потенциала приводит к изменению конвективного профиля в целом, меняя величину средней скорости.

В этом случае, уравнение для скоростного профиля (линейная аппроксимация двух уравнений из системы Пуассона—Больцмана: для распределения потенциала и конвективной скорости по сечению микроканала) примет вид

U ( z ) =

2 Е ^ ее о сЬ( Я ) (   ch( X z ) )

П (   ch(A) J

где в явном виде X = Fh^C ₀ /( ее ₀ RT ) при напряженности продольного электрического поля Е и коэффициенте динамической вязкости п .

Аппроксимация этого профиля степенным

U(Z ) = U max (1 - Z m ),              (3)

что желательно для оценивания моментов аналитических пиков [2], проводится в соответствии с несколькими из возможных критериев оптимизации, связанных с "близостью" двух профилей скорости (2) и (3). При этом степень клиновидно-сти профиля m связана только с параметром X , не зависящим от величины дзета-потенциала, но существенно зависящим от температуры!

Критерий 1

Равенство средней по сечению скорости или равенство интегральной характеристики профиля — толщины вытеснения, определяемой как

5 * = U mx J ( U max - U ( Z ))d z . 0

В нашем случае при равенстве средних скоро- 11

стей имеем J (1 - ch( X z )/ch( X ))d z = J (1 - z^m )d z , 00

что дает оценку m 1 = X / th( X ) - 1. Поскольку при достаточно больших X th ^ 1, то m 1 ~ X - 1.

Толщина вытеснения по приведенной выше формуле для двух указанных профилей (2) и (3) X 1 дает аналогичное равенство----=----.

th( X ) m + 1

Критерий 2

Минимум среднеквадратичного отклонения двух профилей друг от друга.

Минимизация осуществляется по параметру клиновидности профиля m , на основании необходимого условия экстремума

|Г Л ^ ) J t ch( X )

- z^m 1 z^m ln( z )d z = 0. J

Первое слагаемое легко интегрируется после представления гиперболического косинуса рядом Маклорена. Тогда параметр клиновидности вычисляется из уравнения для суммы ряда

У       X² k       =   ch( X )

k ^0 (2 k )!( m + 2 k + 1) ² " (2 m + 1) ² "

Для не слишком больших значений X ряд сходится очень быстро, и достаточно рассматривать несколько первых членов. Данная оценка ( m 2 ) будет несколько отличаться от предыдущей.

Табл. 1. Оценки параметра клиновидности, рассчитанные по различным методикам

X	m 1	m 2	m 3
3	2.0149	2.2253	1.1856
3.5	2.5063	2.7543	1.7691
4	3.0027	3.2677	2.3076
4.5	3.5011	3.7725	2.8348
5	4.0005	4.2732	3.3560
6	5.0000	5.2703	4.3870
7	6.0000	6.2668	5.4077

Критерий 3

Определение параметра клиновидности исходя из равенства другой интегральной характеристики скоростного профиля — толщины потери импульса, определяемой как

5 ** = U max - 2 J U ( ^)(U max - U ( Z))dz .

Для указанных профилей равенство этой харак-

теристики приведет к уравнению

m

сти конвективного скоростного профиля. Так, полагая величину параметра X , соответствующего температуре 280 К, за единицу, получим относительное его увеличение при температуре 345 К на 4.5 %. Таким образом, эффективность управления скоростным профилем с помощью варьирования стационарной температуры в микроканале не будет очень велика. С другой стороны, неконтролируемые (некомпенсированные) колебания температуры в пределах 5–10 К, очевидно, окажут еще меньшее влияние на вариацию скоростного профиля.

1 )

1 (th( X )

. При

A = -

= A,

^ X     ch ² ( X )

решении квадратного уравнения выбирается больший положительный корень.

( m + 1)(2 m + 1)

ВЛИЯНИЕ ВЕЛИЧИНЫ ЭЛЕКТРИЧЕСКОГО ПОЛЯ НА НАГРЕВ ВЕЩЕСТВА В КАНАЛЕ

Динамика трех оценок параметра клиновидно-сти профиля для различных микроканалов (разных

величин X ) представлена в табл. 1.

Оценки существенно отличаются друг от друга, но линейно связаны между собой. Выборочные коэффициенты корреляции между столбцами таблицы будут более 0.9998.

Варьирование величины температуры в малых

В работе [15] выполнено экспериментальное исследование и численное моделирование процесса нагрева микроканала при действии продольного и поперечного электрических полей как источника тепла. При моделировании учитывалась роль кон-

пределах приводит к изменению произведения 5 (T ) = е ( T)T , толщины двойного электрического слоя и клиновидности скоростного профиля. Изменение величины этого произведения с ростом температуры иллюстрируется графиком (рис. 1).

Несмотря на то что диапазон изменения 5 не очень велик, это изменение может быть учтено и использовано. То есть при нагревании в указанных пределах будет происходить незначительное утолщение двойного электрического слоя и произойдет соответствующее изменение клиновидно-

вективного переноса вещества, температуропроводности внутри канала и через его стенку, а также эффекты температурного изменения теплоемкости буфера, коэффициента температуропроводности, динамической вязкости и т.д. В первом приближении полагаем, что тепловое действие электрического поля зависит от характеристик буфера, поскольку теплоемкость последнего существенно больше теплоемкости стенок.

На основании приведенных в работе графиков можно оценить эффективность "чистого" нагрева,

исключив теплоперенос внутри микроканала и уход тепла через его стенки. Тогда нагрев описывается дифференциальным уравнением

p C — = X (T ) CE • E , где р — плотность буфера, d t

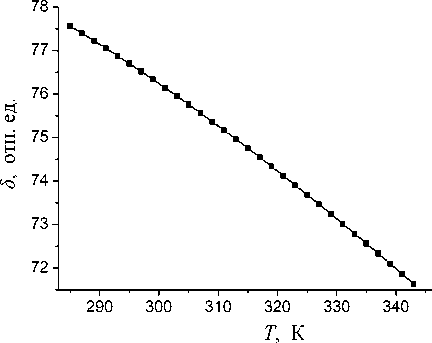
Рис. 1. Температурная зависимость 5 ( T )

С р — удельная теплоемкость буфера (принимаются равными параметрам воды), С — концентрация

буфера, Х ( Т) — молярная проводимость, E — вектор напряженности электрического поля.

Воспользовавшись исходными данными работы [15], проанализируем так называемый "чистый" нагрев, т. е. изменение температуры, вызванное исключительно тепловым действием электрического поля. Скалярный квадрат вектора напряженности электрического поля есть E 1² + E 22 , где Е 1 —

заданная величина напряженности продольного электрического поля, Е ₂ — оцениваемая величина напряженности поперечного электрического поля. Можно утверждать, что E ₂ <  Z 0 / r , где Z 0 — величина дзета-потенциала на поверхности канала, r — радиус канала (потенциал на осевой линии будет меньше, чем на стенке, в пределе — близок к нулю).

Табл. 2. Расчет температуры в канале (эксперимент из [15] и оценка "чистого" нагрева)

В.» с	Е 1 , кВ/м ζ 0 , мВ r , мкм Е 2max , кВ/м	10 50 50 1	15 50 50 1	75 50 10 5
i-Q S 5 рц м	∆ Т чист. , К	0.24	0.55	13.67
	∆ Т эксп. , К	9	28	32
	% эффект.	2.7	2.0	42.7

Результаты расчета влияния "чистого" нагрева представлены в табл. 2. Из приведенных результатов следует очевидный вывод о малости эффекта "чистого" нагрева по сравнению с теплопереносом (как конвекцией, так и теплопроводностью) в случае малых напряженностей электрического поля (до 150 В/см). Таким образом, при медленном анализе (при малых величинах напряженности, главным образом, продольного электрического поля) в первую очередь необходим расчет параметров теплообмена. Заметим, что нами [1–3] использовался режим именно малых напряженностей.

ЗАКЛЮЧЕНИЕ

Таким образом, в рамках описанной выше общей схемы возможна реализация пятого (термического) способа управления микропотоками. Дальнейшая задача исследования будет связана с определением примерных режимов анализа и с созданием и проверкой алгоритмов температурного управления микропотоками на экспериментальных установках.

Можно выделить три стадии (три алгоритма) управления микропотоками при анализе смесей в микроканалах МФАС, упорядоченных по возрастанию сложности их реализации:

Алгоритм 1. Варьирование величины постоянной во всем канале температуры Т , для чего принимаются меры термостатирования микроканала. Сам выбор осуществляется при оптимизации разделения нескольких пиков компонентов. Компоненты смеси, геометрия канала, объем пробы полагаются при этом известными. Как модификация этого алгоритма возможно включение нескольких микрогабаритных нагревателей, позволяющих формировать продольные градиенты теплового поля.

Алгоритм 2. Задаются начальная температура и граничные условия на стенках канала (теплоем- кость, температуропроводность и т.д.). В процессе анализа температура изменяется естественным путем (вследствие теплового действия продольного управляющего электрического поля). Очевидно большее число степеней свободы по сравнению с предыдущим алгоритмом. В качестве модификации данного алгоритма можно рассмотреть циклическое управление температурой, например с помощью скачкообразного его изменения через заданные промежутки времени при использовании естественного нагрева микроканала.

Алгоритм 3. Задание продольного градиента температуры для оптимального управления процессом разделения компонентов. Модификацией этого алгоритма может быть следящая система управления температурой, которая "отслеживает" прохождение быстрых компонентов, характеризующихся более узкими пиками, и меняющая температуру (скоростной профиль, коэффициент диффузии и, следовательно, закон формирования пика более медленных компонентов) с целью сужения пика и достижения лучшего разрешения пиков. Этот алгоритм наиболее сложен в программной и технической реализации, и его возможное внедрение представляется актуальной задачей на перспективу.