Управление мощным лазерным излучением дифракционными элементами нулевого порядка дифракции

Фазовые дифракционные оптические элементы (ДОЭ) не поглощают оптическое излучение, а перераспределяют его по дифракционным порядкам. Это делает их особенно удобными для управления излучением мощных лазеров. В дифракционной оптике обычно в качестве выходного, используется первый или более высокие порядки дифракции, которые распространяются под углом к оптической оси. Нулевой порядок дифракции распространяется без углового отклонения, не имеет ограничения по дифракционной эффективности, что аналогично распространению света через обычные оптические элементы. ДОЭ работающие в нулевом порядке дифракции относительно мало изучены, а их применение ограничено, в основном, цветными фильтрами [1], защитными знаками для кредитных карт [2], поляризаторами [3] и управлением коэффициентом преломления оптического материала [4]. Физические свойства дифракционных решеток нулевого порядка использованы так же в биологии, например, как антиотражающие покрытия глаз некоторых насекомых или цветные узоры на крыльях бабочек. Одно из последних практических применений ДОЭ нулевого порядка - дифракционные фильтры с переменным пропусканием [5,6]. Такие фильтры являются дифракционными аналогами классических нейтральных фильтров переменной плотности и обладают рядом уникальных свойств. Одно из них -возможность регулировки лазерного излучения очень большой мощности. Вопросы, связанные с практическим созданием таких дифракционных фильтров и особенностям их характеристик рассмотрены в настоящей работе.

2.    Дифракционные фильтры.

Световой поток проходя дифракционную решетку (ДР) с прямоугольной формой штрихов разлагается в угловой спектр на ряд дифракционных порядков (рис.1) . Нулевой порядок с интенсивностью 1_ОШ не изменяет направления распространения, а боковые дифракционные порядки с интенсивностью 7* распространяются под углами а_к = кХ/Т к оптической оси, где к - номер дифракционного порядка, Т'-период штрихов решетки, X- длина волны оптического излучения.

В скалярном приближении (Т »Х) интенсивность излучения в нулевом (к=0) порядке дифракции 1_О и фаза У волнового фронта на выходе из одномерной ДР (рис. 1а) описывается выражениями [6]:

Io = MO^l-Q^ 2tQ(l-Q)cos(q>)], (la)

Y = arctg [tQ sin

I, = U(Q*t2+(l-Q2)2+ St^d-Q2)^)!,     (16)

Т = arctg [tQ² sin(p/(l-Q²+tQ²cos ф) ], где (p и t - соответственно, фазовый сдвиг и амплитудный коэффициент пропускания штрихов решетки, d - ширина штриха, Q =d/T - скважность одномерной или двумерной решеток. Фазовый сдвиг определяется глубиной h штрихов решетки : ф=И(п-1)2л/Х где п - коэффициент преломления материала

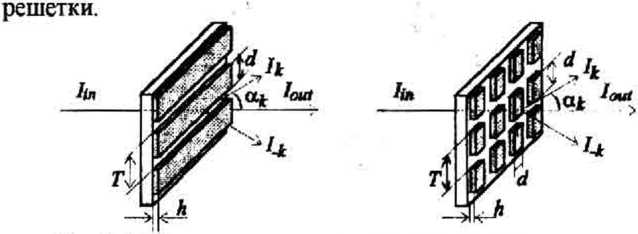
Рис 1 Дифракция света на одномерной (а) и двумерной дифракционных решетках (б)

Из выражений (1) следует, что распределение интенсивности и фазы выходного излучения зависит от геометрических параметров штрихов решетки и длины волны света X. Таким образом, изменяя эти параметры вдоль одной из координат решетки, например х, можно управлять величиной выходного излучения в нулевом порядке дифракции. На этом эффекте и основана работа предлагаемых фильтров. Нулевой порадок дифракции не изменяет направления распространения, не имеет ограничений по дифракционной эффективности (при d=0, 1„ = 1_т ) и поэтому используется как выходной. Коэффициент пропускания дифракционного фильтра

т](х) = Цх)/1ш(х) (2) определяется долей света уходящего за счег дифракции из выходного пучка. Используемая в светофильтре ДР может быть как амплитудная, так и фазовая.

На рис. 2 показаны два варианта выполнения дифракционных фильтров на основе круговых ДР. Фильтр с угловым изменением пропускания (Рис.2а) представляет собой круговую ДР (аксикон) с постоянным периодом по радиусу и скважностью Q^) меняющейся в зависимости от угла поворота. Фильтр с круговым растром ячеек квадратной формы с изменяющейся по углу площадью, показан на рис. 26. Такой фильтр имеет больший динамический диапазон, но также и большее число дифракционных порядков на выходе. Возможен вариант выполнения углового фильтра с радиальными штрихами (типа "звезды Симменса"). Однако период такой решетки будет меняться от центра к периферии, приводя к изменению утла дифракции а, а это не всегда удобно.

Если штрихи ДР непрозрачные (f=OA то из выражения (1) следует, что коэффициент пропускания фильтра зависит только от изменения скважности штрихов решетки вдоль выбранной координаты. Дтя амплитудной одномерной и двумерной ДР коэффициенты пропускания определяется формулами:

П(х,у)= (1-Q(x,y)12 (За)

Л(х.у)= [1-Q2(x,y)j2

Пропускание таких фильтров не зависит от длины волны.

Рис 2 Варианты выполнения дифракционных фильтров на основе «фуговых ДР

Фазовая решетка не поглощает излучение (1=1), а перераспределяет его по дифракционным порядкам Это позволяет придать светофильтру на основе фазовой решетки новые свойства, отсутствующие у классических аналогов - возможность управления (регулирования) очень больших мощностей оптического излучения, например мощных технологических лазеров.

В фазовой решетке штрихи выполнены в виде рельефных углублений в поверхностном слое пластины. Форма рельефа может быть как прямоугольная, так и синусоидальная. Технически проще изготовить фазовую решетку с прямоугольным профилем штрихов, имеющих глубину' h. Коэффициент пропускания светофильтров на основе фазовой одномерной и дву мерной ДР зависит от скважности Q и фазового сдвига у вносимого штрихами и определяется выражениями:

П = Q2 +(1-Q)2+2Q(1-Q)cos(q>), (4а)

7] = Q4+(l-Q2)2+ 2Q2(I-Q2)cos(

Штрихи фазовой решетки выполнены в виде прямоугольных углублений с глубиной, лежащей в диапазоне от h=0 до h=(A/2)/(n-l) для светофильтра работающего на пропускание и до h^'4 дтя светофильтра работающего на отражение.

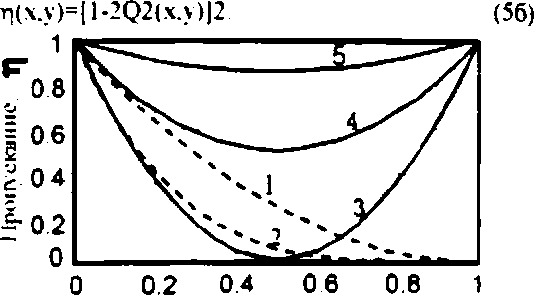
На рис.З показаны зависимости коэффициента пропускания г, дифракционных светофильтров нулевого порядка от величины скважности Q. Коэффициент пропускания амплитудного фильтра плавно изменяется от z; 1 до п 0 при изменении скважности от 0 до 1. Пропускание фазового фильтра (рис. 2а) имеет минимум при О-0.5 для всех значений глубины штрихов решетки (кривые 3-5). Видно, что при рл (кривая 3) диапазон изменения пропускания светофильтра наиболее широкий: от 7=-/ (полное пропускание) при Q=0 до z, 0 (отсутствие пропускания) при Q=0.5. Выражения для коэффициентов пропускания светофильтров на основе од номерной и, соответственно, дву мерной фазовых ДР имеют вид

П(х) = |l-2Q(x)|2.

(5а)

Скважность. Q

Рис 3. Зависимости функции пропускания дифракционных фильтров на основе амплитудных (кривые 1,2) и фазовых (кривые 3, 4, S) решеток от скважности решеток

Дтя получения заданной функции r^x.y^/fx.y) изменения коэффициента пропускания светофильтра в зависимости от координаты х (или утла поворота «Я*, ширина штрихов d решетки кру гового фильтра (рис. 26) должна меняться по следующему закону:

d = T^

1-У7(0) т

где т =/ для амплитудного и т 2 для фазового фильтра Для регулировки лазерного излучения наиболее предпочтительной является линейная зависимость коэффициента пропускания светофильтра от утла поворота fO) -.9.

• 3.    Оптическая система и характеристики дифракционных фильтров

В отличии от классических аналогов (светофильтры с поглощающим слоем переменной толщины), на выходе дифракционного фильтра имеется много дифракционных порядков, которые необходимо экранировать.

Оптическая схема. На рис. 4 приведена схема включения дифракционного фильтра для регулировки излучения мощного лазера. Диафрагма с отверстием для пропускания излучения нулевого порядка и блокирования нерабочих порядков располагается на расстоянии / > D/af. где D - диаметр светового пучка. Если диаметр лазерного пучка 5 мм, период дифракционной структуры фильтра 8 мкм, то для регулировки излучения с длиной волны 1.06 мкм, минимальное расстояние до диафрагмы будет около 40 мм. Для регулировки излучения мощного лазера, между фильтром и диафрагмой необходимо устанавливать поглотитель излучения (в зависимости от мощности - это радиатор с воздушным или водяным охлаждением). Один из дифракционных порядков может быть использован для контроля мощности оптического излучения. Дтя этого в него вносит- ся фотоприемник. Дифракционный фильтр выполняется (для диапазона длин волн 0.25 - 1.06 pin) в виде круглой кварцевой пластине, которая крепится к оси шагового двигателя Быстродействие системы регулировки определяется скоростью вращения шагового привода и составляет 0.05-0.1 сек

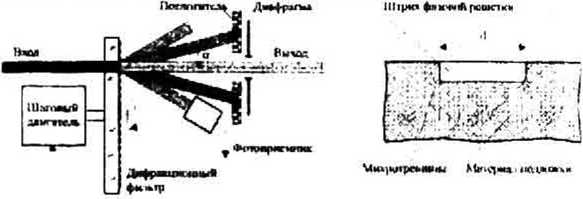
Рис. 4. Схема включения дифракционного фильтра для регулировки излучения мощного лазера (а) и возможное место развития микротрещин (6) под действием импульсного излучения

Дифракционный фильтр нулевого порядка позволяет осуществлять регулировку мощности излучения для непрерывных и энергии импульсов для импульсных .лазеров. Предельная мощность пропускаемого непрерывного излучения определяется в основном материалом подложки и качеством выполнения рельефа дифракционной структуры и превышает 1 кВт/см² в течении длительного времени. Стойкость дифракционного фильтра при многократном воздействии импульсов с большими энергиями (в особенности, режим гигантских импульсов) определяется качеством дифракционной структуры При многократном импульсном нагреве и остывании краев рельефной стру ктуры возможно образование микротрещнн и дальнейшее быстрое разрушение фильтра. Этот эффект отсутствует при регулировке непрерывного излучения.

Динамический диапазон. Динамический диа пазон D^ Г]^ Т]т1П регулировки пропускания определяется для амплитудного фильтра (см. рис.26, выражение (36)) минимально выполнимыми размерами штрихов d^ и периодом их повторения Т:

(^-(г-^/г)2,

а для фазового дифракционного фильтра (46) так же точностью выполнения границ штрихов £ и фазового сдвига ф\

D = d^yC_-£™^^

*  d'^-dW+ld^-d^^v^

где d₀ = —= - £ . Если Т = 10 мкм, £ - 0.1 мкм и d_mm

= 1 мкм, то D_a » 100 и D_Ph ” ЮОО.

4.    Изготовление и испытания дифракционных фильтров

Дифракционные фильтры представляют собой бинарные амплитудные или фазовые структуры. Их изготовление производится по стандартной технологии бинарной оптики:

изготовление фотошаблона - оригинала;

контактное копирование:

формирование рельефной структуры (для фазового фильтра).

Наиболее критическими операциями являются изготовление фотошаблона и копирование. Это связано с тем, что площадь фильтра может быть достаточно большой (сотни смЭ, а минимальные размеры структуры фильтра видимого и УФ диапазонов составляют 0.5-1 мкм.

Фотошаблоны круговых дифракционных фильтров (рис.1) предпочтительно изготавливать с помощью круговых лазерных записывающих систем (КЛЗС), работающих в полярной системе координат [7]. Высокая лучевая стойкость может быть достигнута только при изготовлении фильтров на подложках из кварца.

Рис. 5. Фрагменты хромовых фотошаблонов дифракционных фильтров: с линейными штрихами (а), круговой решеткой (б) и двумерным растром (в)

На рис.5 приведены фрагменты .хромовых фотошаблонов различных фильтров изготовленных с помощью КЛЗС. На рис.5а приведен пример записи линейной решетки с постоянным периодом (Г = 6 мкм) и шириной линии изменяющихся от 1 до 5 мкм (а). Линейная решетка изготовлена на КЛЗС по термохимической технологии. Хорошо видны искажения прямых линий вызванные круговым сканированием записывающей системы. Круговые решетки записываются со значительно более высоким качеством. На рис. 56 показан фрагмент кругового фильтра (рис. 1а) в области изменения градации пропускания. Хорошо видна дискретность s перемещения записывающего лазерного луча (размер записывающего пятна - 0.8 мкм), которая составляла 5=0.2 мкм. Дискретность записи приводит к скачкообразному изменению коэффициента пропускания фильтра. Так. например, для фазового фильтра при 7- 10 мкм, г/=2мкм, 5=0.2 мкм, дискретность изменения пропускания составит А?) =0.05. Однако из-за достаточно большого размера апертуры входного пучка, эта дискретизация усредняется и не сказывается на изменении интенсивности выходного пучка. На рис. 5в показан фрагмент поверхности амплитудного дифракционного фильтра. На рисунке показана область изменения пропускания от q = 0.05 до q = 0.1.

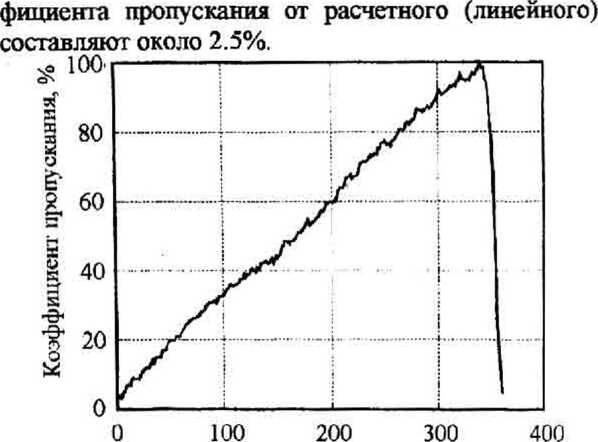
Измерение коэффициента пропускания экспериментальных образцов амплитудных фильтров производилось по схеме рис.4а. В качестве источника излучения использовался He-Ne лазер, а фотоприемник устанавливался в выходной пучок нулевого порядка. Измерение величины прошедшего излучения осуществлялось при повороте фильтра через каждые 1.8° (200 шагов на оборот). Зависимость коэффициента пропускания 7 одного из образцов амплитудного фильтра от угла поворота а приведена на рис.6. Динамический диапазон этого образца фильтра составлял />=20. Закон изменения пропускания фильтра от угла поворота - был задан линейный. Видно, что максимальные отличия коэф-

Угол поворота, i-рад

Рис 6 Зависимость коэффициента пропускания кругового амплитудного фильтра от угла поворота.

Диаметр фильтра - 50 мм, размеры области решетки 20-46 мм, период дифракционной структуры - 8 мкм

Фазовые дифракционные фильтры изготавливались ионным травлением кварцевой подложки. В качестве защитной маски использовался хромовый рисунок, который переносился методом контактной фотолитографии с фотошаблона - оригинала. Особое внимание уделялось уменьшению рассеяния света на травленой поверхности. На рис. 7 приведены типичные микрофотографии фрагментов поверхности фазовой дифракционной решетки с периодом около 16 мкм и глубиной 1 мкм. Условия травления следующие: газ - аргон, давление - 1 Па, напряжение - 700В. время травления - 60 мин.

Одна из важнейших характеристик дифракционного фильтра является его лучевая стойкость. Лучевая стойкость исследуемых фильтров проверялась с помощью схемы приведенной на рис. 8а. Излучение мощного лазера направлялось на исследуемый образец фильтра. Для увеличения плотности энергии, использовалась длиннофокусная линза. В этуг же точку под небольшим углом направлялось излучение контрольного маломощного лазера. На выходе фильтра измерялась величина излучения контрольного лазера, которая зависела от степени разрушения поверхности мощным лазером.

Образцы амплитудных и фазовых фильтров исследовались на стойкость к импульсному излучению (Х=1.06 мкм) большой мощности. На рис. 86 показаны зависимости изменения пропускания амплитудного (кривые 1, 2) и фазового (кривая 3) фильтров (кварцевая подложка) под действием последовательности импульсов длительностью 15 нс и энергией, соответственно, 0.05, 0.024 и 10 Дж/см2 Видно, что поверхность фильтров с хромовым покры тием (толщина около 800 нм), начинает разрушаться при достаточно низких энергиях импульсов. Изменений в пропускании фазового фильтра, выполнен-ного на кварцевой подложке, в диапазоне энергий до 10 Дж/см2 не обнаружено. Изменения поверхности фильтра так же не обнаружено.

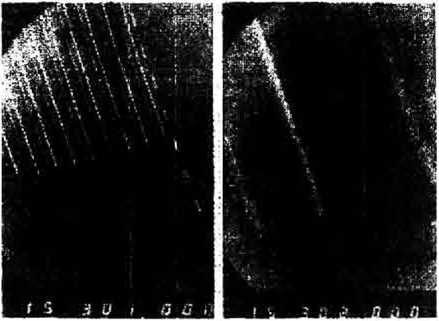
Рис. 7. Микрофотографии (SEM) фрагментов Поверхности фазовой решетки (период 16 мкм) при различном увеличении

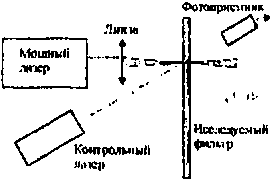
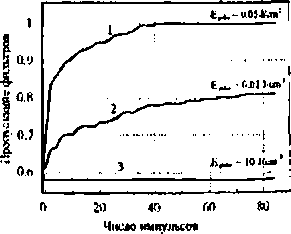
Рис. 8. Схема (а) измерения лучевой стойкости дифракционных фильтров и зависимость (6) изменения пропускания фильтров от числа импульсов мощного лазера

5.    Выводы

Работающие в нулевом порядке круговые дифракционные фильтры позволяют регулировать мощность проходящего сквозь них лазерного излучения в большом динамическом диапазоне. Регулировка обеспечивается путем вращения фильтра. Область применения фильтров - регулировка излучения мощных непрерывных и импульсных лазеров.

Основные преимущества дифракционных фильтров по сравнению с классическим аналогами: - регулировки излучения очень большой мощности; - любая заданная зависимость коэффициента пропускания от угла поворота;

• -    простота технологии изготовления - контактное копирование и ионное травление;

• -    нечувствительность к поляризации входного излучения.

В работе продемонстрирована возможность создания дифракционных фильтров с линейной зависимостью коэффициента пропускания от угла поворота и высокой лучевой стойкостью.