Управление нагрузкой на сети ЭВМ распознаванием и моделированием трафика

При анализе результатов моделирования реальных сетей часто приходится сталкиваться с большим разбросом параметров моделирования и реальных параметров сетей. При анализе сложных сетевых структур в большинстве случаев применяют классический подход с использованием пуассоновских потоков заявок и экспоненциальное распределение времени обработки заявки. Однако в большинстве случаев сложных высоконагруженных сетей такой подход дает лишь очень приближенный результат. Поэтому для повышения точности моделирования сетей необходимо определять не только первые несколько моментов распределения интервалов поступления и обслуживания, но и сам закон распределения этих величин. В высоконагруженных сегментах, особенно в серверных пулах, закон распределения времени поступления заявки неэкспоненциальный [5]. Кроме того, он может изменяться в зависимости от времени суток, ситуации в других доменах сети (в случае динамической маршрутизации) и т.д. В данной работе также подтверждается неэкспоненциальность распределения трафика.

Постановка задачи и пути ее решения

В случае анализа сложных сетей с логическим и физическим сегментированием, в которых присутствуют неоднородные потоки трафика, сервера, маршрутизаторы и маршрутизирующие коммутаторы, необходима декомпозиция на простые сегменты. При этом каждый сегмент должен содержать не более одного нелинейного устройства (маршрутизатора или интеллектуального коммутатора). Все остальные сегменты сети будут для данного сегмента внешним трафиком. После такой сегментации сети уже можно анализировать каждый сегмент в отдельности (сверху вниз), а потом от простейших сегментов перейти к анализу всей сети (снизу вверх). Схема одного сегмента представлена на рис. 1.

Данный сегмент является простейшей единицей в сложной сегментированной сети. Он может не иметь сервера или брандмауэра, однако в нем всегда должны быть рабочие станции и коммутатор.

Маршрутизатор

Рабочая станция

Рабочая станция

Рис. 1. Схема одного сегмента сети

Рабочая стан

Сервер

чая станция

Рабочая станция

Рабочая станция

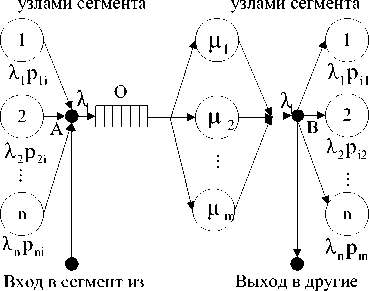
Представим этотсегмент в виде «простейшей» сети СМО. Получится схема, показанная на рисунке 2. Для каждого узла сети можно построить подобную схему. Здесь точка А называется точкой композиции (мультиплексирования) потоков, а точка В – точкой декомпозиции (демультиплексирования). В этих точках по закону равновесия потоков              .

i вх i вых

Генерация пакетов

Приём пакетов

сегменты других сегментов

Рис. 2. Структура i -го узла сегмента сети

Исходная сеть сегментируется по следующему критерию.Если в центре сети стоит управляемый коммутатор второго или третьего уровня, то все узлы, подключенные к одному порту, будут находиться в одном сегменте. Если же в сети используется маршрутизатор и несколько подсетей, то все сегменты из одной подсети впоследствии требуется объединить в один сегмент более высокого уровня

Для расчета характеристик одного сегмента воспользуемся результатами [1-2].При этом наиболее важную роль будет играть согласованность коэффициентов двумерного диффузионного процесса a ₁ , a ₂ , b ₁ , b ₂ и матрицы Р – вероятностей передач заявок реальным данным сети [1].Эти коэффициенты процесса можно легко выразить через среднее и дисперсию реальных времен поступления и обработки пакетов. Однако необходимо учитывать, что в реальной сети среднее время между поступлениями пакетов будет функцией времени, каждый узел имеет циклическое распределение нагрузки на сеть в течение суток. В нерабочее время большинство узлов генерируют только фоновый широковещательный трафик, а в рабочее время существует зависимость от продолжительности рабочего дня.

Реальные измерения нагрузки на сеть

На рис. 3 показано поведение выборочного среднего количества пакетов в минуту для офисного работника, использующего сеть, в обычный день на протяжении с 9:00 до 21:00. Как видно из графика, существует 2 пика активности, один провал (обед) и наблюдается четкая закономерность в остальные периоды. В ночное время трафик данного узла будет колебаться около нуля.

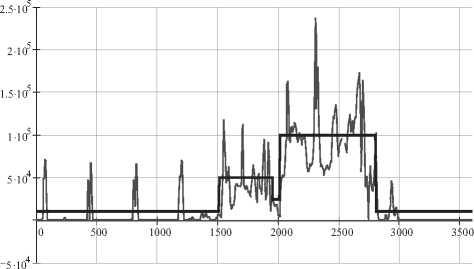
Рис. 3. Трафик узла офисного работника

Данное поведение является характерным для этого вида узлов и для упрощения расчетов может быть разбито на четыре неравные зоны:

1 зона – нерабочее время (вечер,ночь,раннее утро).В это время офисная работа в большинстве своем не ведется,трафик минимален.Пики трафика свидетельствуют об обновлении антивирусных программ и операционных систем (рис.4).Трафик распределен по закону гамма- распределения.

2зона – до обеда.Трафик постепенно растет,к обеду принимает величину первого пика (распределение нормальное - рис. 5).

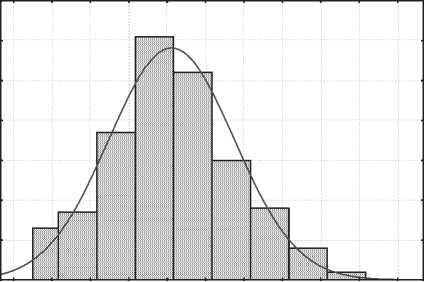
• 3    зона – обед. Трафик заметно снижается,дости-гая своего минимума за рабочий период.На данном графике он не очень продолжителен (распределение гамма - рис.6).

• 4    зона – вторая половина рабочего дня.Трафик на-растает,достигая к 4-5 часам дня своего максимума. Функция распределения – гамма (рис.7).В это время сеть испытывает самые большие нагрузки.Все дневные отчеты,все операции с бумагами,электронными хранилищами должны быть завершены до конца рабочего дня,что предполагает одновременное обращение к центральным серверам многих подсистем.

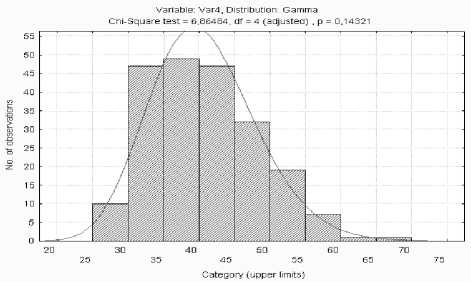
Рис. 4. Гистограмма распределения в зоне 1

Variable: Var2, Distribution: Normal

Chi-Square test = 5,83206, df = 5 (adjusted) , p = 0,32290

-1200     0     1200    2400    3600    4800    6000    7200    8400    9600   10800

Category (upper limits)

Рис. 5. Гистограмма распределения в зоне 2

Variable: Var2, Distribution: Gamma

Chi-Square test = 5,35280, df = 5 (adjusted) , p = 0,37436

| 40

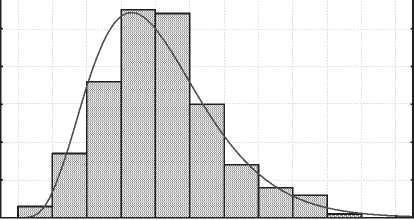
0     1000   2000   3000   4000   5000   6000   7000   8000   9000  10000 11000

Category (upper limits)

Рис. 6. Гистограмма распределения в зоне 3

Variable: Var2, Distribution: Gamma

Kolmogorov-Smirnov d = 0,08097, p < 0,01 Chi-Square test = 7,75294, df = 4 (adjusted) , p = 0,10106

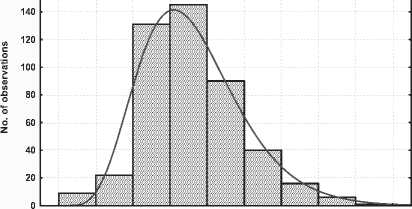
0,0000        4888,8889      9777,7778      14666,6667     19555,5556

2444,4444      7333,3333      12222,2222     17111,1111     22000,0000

Category (upper limits)

Рис. 7. Гистограмма распределения в зоне 4

Съем данных о трафике производился с помощью протокола SNMPс отдельного порта коммутатора, к которому подключена рабочая станция. Трафик серверов и коммутаторов будет являться результатом агрегирования трафика отдельных рабочих станций (в данном сегменте – 54 станции).

Разделение трафика на зоны значительно упрощает вычисление средних значений и дисперсий времени между пакетами, необходимых для расчета характеристик сегмента..

Пример параметров распределений трафика за день представлен в таблице 1.

Таблица 1. Параметры распределения трафика

Зона	Распределение	Параметры
1	Гамма	α = 5,33 β = 234
2	Нормальное	m = 4101 σ = 60
3	Гамма	α = 6,41 β = 679
4	Гамма	α = 6,88 β = 1289

По этой таблице легко можно вычислить средние значения и дисперсии распределения времени между пакетами.

Моделирование сети

Моделирование сети ставит перед собой задачу изучить характеристики модельной сети, прогнать различные режимы работы, дать нагрузку на какие-либо ее части. Все это обычно предшествует созданию сети (чистая модель) либо ее модернизации. В реальной сети соединения непосредственно между конечными пользователями – явление не такое уж и частое. В большинстве своем пользователи обращаются к серверам. Это подтверждается проведенным исследованием сети Оренбургского госунивер-ситета (ОГУ) и ООО «Энергосбыт».

Исследования проводились путем сбора статистики со всех коммутаторов, которые это позволяли (в случае ООО «Энергосбыт» это 100% коммутаторов), и анализировались направления потоков трафика с помощью снифферов и технологии «Man-In-Middle Switching Environment».

Результат анализа потоков за 3 месяца в ОГУ показан в таблице 2.

Все основные потоки трафика курсируют или через центральный коммутатор, или в пределах одного сегмента, ограниченного портом центрального коммутатора. Весь трафик между разрозненными пользователями не превышает 6,5%, причем 5,1% из них – это широковещательный трафик. 64% всего трафика проходит через центральный коммутатор (к серверам), 35% трафика локализируется в пределах сегментов кафедр.

График загрузки сетевых каналов крайне неравномерен, однако закономерности все же присутствуют. Аппроксимированный по принципу наименьших квадратов в среде Mathcad график загрузки центрального коммутатора за день на сегменте показан на рис. 8. По оси Х показаны секунды, по Y – загрузка коммутатора в пакетах/с.

Таблица 2. Структура трафика сети ОГУ

C3 R ^ & к r H	r к Ei M cd Ph R СУ m	r Ph 2 «1 ;S « Ц IO l=5 C	^ s & s m ^ R § О 4 c	Ю LO О
HTTP	От прокси-сервера к клиентам	10	11	29 308,91
	Запросы клиентов к прокси-серверу	0,04	0,03	117,24
	От локального вебсервера к клиентам	1,2	1,0	3 517,07
FTP	Запросы к локальному файл-серверу	7,2	7,0	21 102,41
	От файл-сервера к клиентам	13,8	13,4	40 446,29
	Запросы к серверам кафедр	2,5	2,6	7 327,23
	От серверов кафедр к клиентам	10,1	10,1	29 602,00
SMB	От файл-сервера к клиентам	10,3	10,8	30 188,18
	От сервера кафедры ПОВТ к клиентам	5,9	5,6	17 292,26
	От сервера кафедры ВТ к клиентам	7,8	7,8	22 860,95
	От сервера кафедры ПИ к клиентам	8,9	8,4	26 084,93
E MAIL	От клиентов к серверу	5,6	5,0	16 412,99
	От сервера к клиентам	7,2	7,0	21 102,41
Netbios	Широковещательный	5,1	5,8	14 947,54
TCP- Oracle	От сервера к клиентам	2,1	2,0	6 154,87
TCP-Print	От клиентов к принт-серверу	0,5	0,2	1 465,45
TCP- Other	Между клиентами	1,1	1,8	3 223,98
UDP- Other	Между клиентами	0,2	0,3	586,18
Other	Между клиентами	0,1	0,12	293,09
		99,64	99,95	300123223

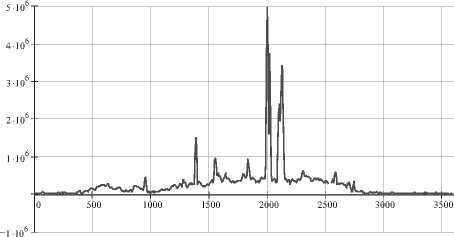
Рис. 8. График дневной загрузки центрального коммутатора

Ночью загрузка близка к нулевой – в сегменте работает только сервер. Утром скачкообразно загрузка повышается при включении всех компьютеров, вечером работу начинают вечерники. Естественно, функция распределения такого трафика не относится к тривиальным.

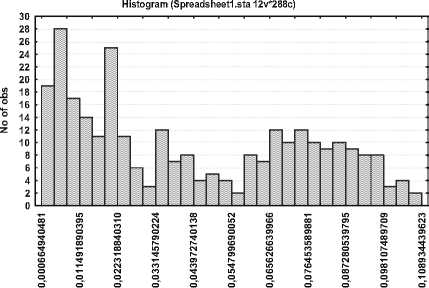
Var10

Рис. 9. Гистограмма распределения количества пакетов на коммутаторе

На рис.9 показана гистограмма загрузки коммута-тора.Как видно,закон распределения здесь комбини-рованный.Как моделировать такое распределение?

Разобьем весь интервал на несколько зон.Затем определим законы распределений на каждом из интервалов по аналогии с вышесказанным.

На каждом интервале необходимо определить форму распределения: сам закон и его первые два момента.Для этого выберем наиболее подходящий закон распределения (по виду)и проверим его согласованность по критериям Колмогорова и Пирсона, детализируя трафик на участках.

Детализация трафика (гистограмма)показана на рис.10.Она практически совпадает с результатами, полученными выше в п.3.Для автоматического определения закона распределения пакет «Статистика» в полной мере не подходит,так как за один раз тестируется только одна выборка.

Поэтому для частого распознавания законов распределений авторами разработаны алгоритм и программа тестирования результатов замеров трафика.

XAri able: XAr1, Distribution: Gamma

Chi-Square test =19,86056, df = 1 (adjusted) , p = 0,11169

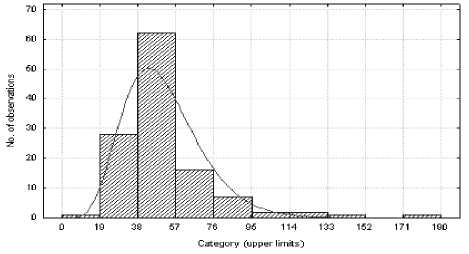
Рис. 10. Детализация трафика на одном из участков

Те исследователи, кто неоднократно в своей практике пытался идентифицировать закон распределения, связанный с конкретной выборкой, убедились, что достаточно часто используемый критерий согласия не дает оснований отвергать целый ряд законов распределений. Способность критерия различать близкие альтернативные гипотезы определяется его мощностью. Именно недостаточная мощность критерия не позволяет принимать окончательное решение.

Идентификация закона распределения происходит по следующему алгоритму:

– ограничение множества «подходящих» распределений;

– определение для каждого закона распределения из данного множества оценок неизвестных параметров и проверка гипотез о согласии полученного закона распределения с исходными данными;

– выбор того закона распределения, согласие с которым наиболее вероятно [4].

Основным методом оценивания параметров распределений, заложенным в системе, является метод максимального правдоподобия. Оценки параметров распределений находятся в результате максимизации функции правдоподобия по частично группированной выборке. Эта функция имеет вид:

L(o) = Пp(xi»®), где P^’ ®) — n вероятность того, что случайная величина Х примет значение xi, n – количество интервалов дискретизации гистограммы; Q - множество допустимых значений.

Проверка гипотезы о согласии осуществляется по ряду критериев: отношения правдоподобия X2 Пирсона, Колмогорова - Смирнова и др. Решение о степени соответствия выборки с законом распределения принимается по их совокупности. При проверке гипотез о согласии проверяется гипотеза вида H o : f (x, 0) = f (x, 0 ).

В принятой практике статистического анализа проверка осуществляется по следующей схеме. Для выбранного критерия вычисляется оценка S* как некоторой функции от выборки и закона распределения f (x,0). Далее сравнивают полученное значение статистики S* с критическим для данного уровня значимости S_α . Нулевую гипотезу отвергают, если S* >  S_α .

Например, статистика критерия согласия X Пирсона при истинной гипотезе Ho в пределе подчиняется X — распределению с числом степеней свободы k – 1, если по выборке не оценивались параметры, и с k – m – 1 , если по ней оценивались параметры закона распределения.

Для непараметрических критериев Колмогорова-Смирнова предельные распределения статистик известны только для ситуации полностью определенных законов распределения f(x, 0).

Для примера возьмем сначала гамма-распределение, так как известно, что данные взяты из сетей связи. Плотность распределения

- α α - 1 - x /β xe

f ( ^{x )} = <

г ( а )

1 0,

x >  0;

x <  0,

тогда числовые характеристики (математическое ожидание и дисперсия): M ( X ) = ав, d ( X ) = ав 2.

В результате получаем теоретическое распределение, показанное на рис. 11.

triable: Xtirfl, Distribution: Gamma

Kolmogorov-Smirnov d = 0,18433, Chi-Square test = 16,13193, df = 8 (adjusted), p = 0,14053

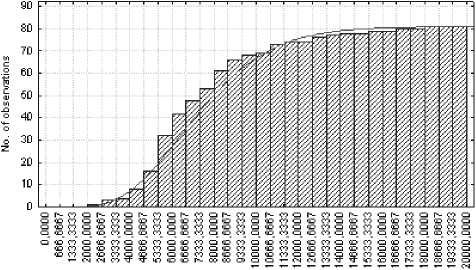
Category (upper limits)

Рис. 11. Теоретическое и эмпирическое распределения

На данном рисунке параметр Scale гамма-распределения (α) в пакете «Statistica 6» равняется 4240,53, параметр Shape (β) = 1,8236.

Вычисленные по приведенной ниже методике соответствующие параметры равны 4280 и 1,8245 соответственно, что показывает практическое совпадение результатов.

Полученная вероятность p = 0,14 позволяет согласиться с тем, что гипотезу о гамма-распределении можно принимать. После проверки по одному критерию следует проверка по другому критерию, например по критерию χ ² Пирсона.

После сравнения вероятностей по всем критериям принимается решение о соответствии закона распределения. Все эти данные (параметры законов распределения, вид закона) необходимы для точного анализа сети и моделирования процессов в ней [1-2].

Поприведеннымвышеалгоритмамбыласозда-на программная система с библиотекой распределений на кроссплатформенном языке FreePascal, и она прошла апробацию в реальных условиях на сервере биллинга. Апробация показала высокую эффективность данного подхода при анализе больших массивов данных о трафике.

Воспользуемся детализированными данными о трафике ОГУ для анализа производительности и загрузки оборудования. Для удобства возьмем центральный коммутатор и самых крупных (по активности) клиентов. После анализа характеристик трафика в каждом узле сегмента определяем коэффициенты вариации времени между пакетами и интенсивность их поступления. Однако, зная закон распределения, необходимо делать поправки при определении первых двух моментов для корректировки недостаточной длины выборки. После определения всех характеристик и матрицы вероятностей производим расчет. Результаты для fTP трафика показаны в таблице 3.

Таблица 3. Расчет характеристик сети

kJ м Л о К	5	kJ § ср Н с 5 kJ kJ со Л	§ и " со О	2 kJ Д 1) СО	kJ ^ S S и о	РЭ 09 О ° и § У ° ® ® о
1	Файл- сервер	0,62	0,58	3	1,6	9,6
2	Email	0,58	0,4	3	1,3	7,6
3	Proxy	0,73	0,7	5	2,8	2
4	Сервер ПОВТ	0,37	0,43	4	0,55	1,8
5	Сервер ПИ	0,43	0,39	3	0,73	3
6	Сервер ВТ	0,35	0,33	2	0,5	1,6
7	Oracle	0,4	0,42	7	0,63	2,2
8	Роутер	0,93	0,87	4	14	13

Заключение

• 1.    Таким образом, результаты моделирования, приведенные в таблице 3, получены путем идентификации реального трафика сети и оцен-

  Таблица 4. Зависимость среднего времени ожидания заявок W в узле от ρ, С μ , C λ

  		W
  ρ	С μ С λ	0,1	0,5	1,0	2,0	5,0
  0,1	0,1	0,005	0,015	0,046	0,175	1,106
  	0,5	0,101	0,104	0,109	0,195	1,205
  	1,0	0,112	0,117	0,149	0,252	0,318
  	2,0	0,117	0,220	0,334	0,713	2,601
  	5,0	2,211	2,939	3,306	4,862	9,764
  0,3	0,1	0,007	0,046	0,132	0,531	4,820
  	0,5	0,049	0,066	0,169	0,731	5,080
  	1,0	0,114	0,173	0,348	1,015	5,538
  	2,0	0,726	0,816	1,133	2,080	6,990
  	5,0	12,072	13,536	13,556	14,202	19,472
  0,5	0,1	0,011	0,068	0,342	1,689	11,857
  	0,5	0,068	0,152	0,475	1,892	12,214
  	1,0	0,339	0,482	0,890	2,428	12,867
  	2,0	2,406	2,408	2,822	4,529	15,291
  	5,0	21,897	21,842	22,265	24,070	34,889
  0,7	0,1	0,021	0,205	0,977	4,352	28,373
  	0,5	0,206	0,456	1,288	4,699	28,927
  	1,0	1,084	1,359	2,264	5,760	30,066
  	2,0	5,701	5,881	6,748	10,192	34,520
  	5,0	38,942	39,133	40,072	43,943	68,701
  0,9	0,1	0,071	1,126	4,386	17,665	111,022
  	0,5	1,218	2,250	5,540	18,813	112,570
  	1,0	4,716	5,789	9,107	22,402	116,088
  	2,0	19,150	20,151	23,569	36,947	130,341
  	5,0	122,476	123,449	126,918	140,740	235,218

  
  

• 2.    После оценки характеристик распределения трафика, для быстрого прогнозирования задержек в узлах сети, а затем и других характеристик сети можно бы было воспользоваться также готовыми результатами [1-2]. Имеется в виду таблица 4 значений среднего времени ожидания, полученная для широкого диапазона изменения коэффициентов вариаций распределений времен поступления и обслуживания. Учитывая тот факт, что основные характеристики сети являются производными от времени ожидания, их значения можно получить по этой таблице путем интерполирования.

• 3.    Разработанная библиотека охватывает класс, состоящий из 26 непрерывных законов распределений случайных величин, наиболее часто используемых в приложениях. Эти виды распределений: экспоненциальный, нормальный, Рэлея, Максвелла, Парето, Эрланга, Лапласа, нормальный, логарифмически нормальные (ln и lg), Коши, Вейбулла, двойной показательный, гамма-распределение и др.

• 4.    В результате исследований были изучены методы автоматического распознавания зако-

• нов распределений случайной величины,при-менения на практике данного метода. Результаты расчета проверены пакетом «Statistica 6» и обладают высокой достоверностью. Точность моделирования сетей с использованием метода двумерной диффузионной аппроксимации повышается благодаря корректировке моментов в соответствии с законами распределений.

ки характеристик его распределения. Эти оценки явились исходными данными для применения методики [1-2] к анализу компьютерных сетей. Фактические результаты по загрузке здесь получены путем измерения трафика сети. Такое совпадение результатов моделирования и измерений можно считать вполне приемлемым.