Управление ориентацией и разгрузка накопленного кинетического момента инерционных исполнительных органов космического аппарата на высокоэллиптической орбите

В работе рассматривается движение космического аппарата (КА) с инерционными исполнительными органами (ИИО) на высокоэллиптической орбите (ВЭО). Для таких орбит характерно деление на два участка: рабочий (в окрестности апогея) и дежурный (в окрестности перигея). Далее в работе речь будет идти о дежурном участке, на котором осуществляются вспомогательные динамические операции. Одной из таких операций является разгрузка накопленного на ИИО кинетического момента. При насыщении системы ИИО КА применяют различные способы разгрузки накопленного кинетического момента. Обычно управление центром масс КА и разгрузка ИИО автоматических КА производится с использованием ракетных двигателей малой тяги, в т. ч. электроракетных [1]. Естественно, наиболее предпочтительными способами управления кинетическим моментом ИИО являются безрасходные способы, использующие моменты малых сил, действующих на КА [2–4].

Целью данной работы является решение задачи управления ориентацией и разгрузки кинетического момента КА с ИИО на ВЭО по всем трем каналам управления с использованием гравитационного момента и с применением алгоритма точного размещения полюсов.

математическая модель ка

Для вывода уравнений, описывающих динамику углового движения КА, введем две системы координат:

• •    орбитальная система координат (ОСК), начало которой совпадает с центром масс КА, ось OY _ОСК направлена вдоль радиуса-вектора, OX _ОСК лежит в плоскости кеплеровой орбиты и составляет с вектором линейной скорости острый угол, OZ _ОСК дополняет систему до правой. Рабочая орбита и оси ОСК, а также два участка, на которые делится орбита: рабочий и дежурный, представлены на рис. 1.

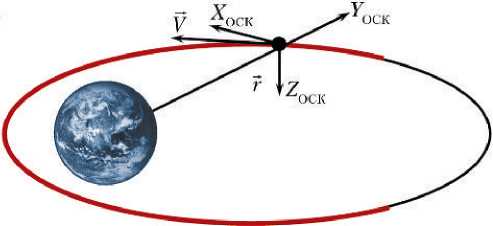
Рис. 1. Рабочая орбита и оси орбитальной системы координат: — — дежурный участок; — — рабочий участок

• •    связанная с КА система координат (ССК) c началом в центр масс КА. Для упрощения математических выкладок оси ССК совпадают по направлению с главными центральными осями инерции КА.

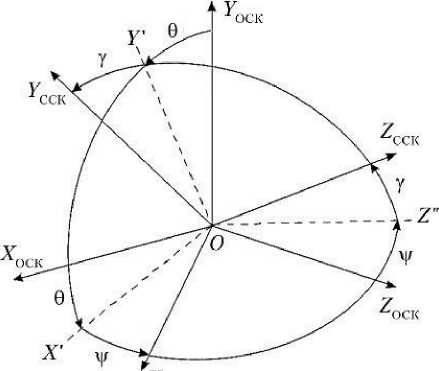
Для перехода от ОСК к ССК необходимо выполнить три последовательных вращения (рис. 2). Первое вокруг начального положения оси OZ _ССК ( OZ _ОСК) — тангажный разворот на угол θ, второе вокруг промежуточного положения оси OY _ССК ( OY ') — разворот по каналу рыскания на угол ψ и вокруг конечного положения оси OX _ССК — разворот по крену на угол γ.

V сск

Рис. 2. Взаимное положение осей орбитальной и связанной систем координат

Ниже представлены уравнения, описывающие движение КА около центра масс.

• 1.    Кинематические соотношения в кватернионной форме [5]:

• 2.    Динамические уравнения углового движения КА, несущего вращающиеся массы, при воздействии гравитационного момента [6]:

2ЛССК = Лсск° (со , ) — (со ) ° Лсск (1 , (1)

где — кватернион разворота от ОСК к ориентации, требуемой для разгрузки; — абсолютная угловая скорость в проекции на ССК; — орбитальная угловая скорость в проекции на ОСК.

J ω_абс + ω_абс × J ω_абс+ h + ω_абс × h = M grav , (2) где J — тензор инер ц ии КА; h — вектор кинетического момента ИИО; M_grav — гравитационный момент.

Далее:

• •    проецируем уравнение (2) на оси ССК;

• •    предполагаем малыми углы крена и рыскания, а также производные по времени от углов крена, рыскания и тангажа;

• •    применяем теорему об изменении кинетического момента отдельно к корпусу КА и отдельно к вращающимся элементам конструкции;

• •    производим замену переменных ω₀, ω₀, r на переменные и параметры кеплеровой орбиты (эксцентриситетом, истинной, эксцентрической и средней аномалией);

• •    линеаризуем полученную систему уравнений около углового положения (0, 0, θ₀).

Таким образом, линеаризованные уравнения углового движения КА при наличии ИИО для эллиптических орбит при учете действия гравитационного момента в случае применения теоремы об изменении кинетического момента [7] в соответствии с работами [8, 9] имеют вид:

..

γ

..

ψ

J – J yy zz

J xx

G r3 (

+ G [2ES r 3

v

G e co sν) + r 3₃

у-З| ^Jyy J

V J x

л

² θ₀ γ

s

Jxx + Jyy – Jzz os xx

9 о + 9с

G . r ^G ₃ ( 1 + e c o sν)ψ

I v J ’

2         xx

J – J xx zz

Jyy

G r3 (

e co sν)

G _{3 r} 3

² θ₀ ψ

+s

J + J – J _n xx yy zz

Jyy

G r 3 (

+ e co sν) ^. γ

( J J

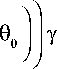
u У

Jyy

G                  xx zz

2es v + 31-------- -s   0n+ 9c r                   J I 2

• V            ^v yyy ^{2 v}

hi + G^( e° v)h„ = uT, x r 3

.G h   JG1 1 + ecijsv hi = u , y V r3 V' x y

..             J J u z

T= ’

G yy xx           3 G yy xx

• 9-    3^^- — --- cos20„+-^—ч -- у --- sin20„  2 ^- e sinv

3                           0           3                           03

r       Jzz                      r       Jzzr

.

hz = uz где Jxx, Jyy, Jzz — главные центральные моменты инерции КА; hx, hy, hz — проекции кинетического момента ИyИОz на оси связанного базиса; ux, uy, uz — моменты реакции в подшипниках маховиков, через которые осуществляются как управляющее воздействие на корпус КА с целью поддержания его ориентации, так и разгрузка накопленного кинетического момента ИИО; γ, ψ, θ — углы отклонения связанного базиса от орбитального по крену, рысканию и тангажу, соответственно; ϑ — малый угол отклонения от углового положения (0, 0, θ0) в канале тангажа, ϑ = θ – θ0; r — радиус-вектор центра масс спутника относительно центра Земли; ν — истинная аномалия; е — эксцентриситет орбиты; G = μM; μ — гравитационная постоянная; M — масса Земли.

Из этих уравнений видно, что пространственное угловое движение КА разделяется на два: плоское движение в канале тангажа и неразделяющееся движение по каналам крена и рыскания.

При переходе в пространство состояний с вектором состояния x перепишем систему (3) таким образом, чтобы элементами матрицы М_i в соответствующем канале управления являлись элементы, не относящиеся к этому каналу. Тогда система уравнений (3) распадется на три системы вида:

x. = A . x i + B i u. + M i , i = x, y, z (4)

A = i

( ⁰

a . 21

к

x =

I

a x 21

a y 21

^mx 21

G + r 3

( J J J

к

(

2 e si nv к

^my 21

G r ³

к

J xx         7

G .

— (1 - e o jsv )v +

J – J

3 J ²² ! 1_{S1 n29} 0   .

к ^xx   7 к ²

θ0 ψ ;

G

J+ J – J

J^xx J yy J^zz G                . .

-----J------- \^ ⁽ e^{C V)Y}

V       yyy        7

(

2 e si nv + 3

V

Г J — J ) xx zz

J

V yy 7

1-si i:2Oo

ϑ c

2θ0 γ ;

G

J – J yy xx m221^271 —J--- sin(200)  2r^ esiIW;

zz

m

x 31

(1 + e cosv) h y ;

m , = (-^( l + e cosv) h ; m = 0. y 31        r 3                     x    z 31

построение законов управления

В пространстве состояний задача ставится следующим образом. Для линейной динамической системы со многими входами и выходами x = Ax + Bu,

T i...

" h

0 hld к 7

J – J yy zz

J

V x xx 7

J – J xx zz

J

V yy 7

a z 21

0 )

^B i

M = г

^mi 21 ^mi 31 0

J

J zz

>

GG

— ( 1 + e o?sv ) - 3 — cos²0

Г 3                      r 3

G               G . ^

—7 (1 + e cosv) + 3   si n²0_n

Г 3 '                      r ³        и

J – J 3 G yy xx

r 3

V

J zz   7

cos(2 60);

где x — n-мерный вектор, u — r-мерный вектор входа, матрица B(n×r) имеет полный ранг по столбцам, а множество собственных значений матрицы А равно eig(А) = {Xi е С: det(XIn - A) = = 0, i = 1 ,..., n}, требуется найти такой закон управления с обратной связью u = Kx, где K — матрица регуляторов по состоянию, чтобы множество собственных значений матрицы замкнутой системы лежало в левой полуплоскости комплексной плоскости.

В данном случае мы имеем:

x -A.x. + В u + M., i = x, y, 2:, i i i i i i и = к. x.

В канале тангажа система (5) имеет вид: x- A 2 _Z + B ₂ K) x_z + M z .

Рассмотрим случай, когда свободный член в уравнении для канала тангажа равен нулю: m_{z 21} = 0,

3 G (Jyy^-              „ G „

------- sin(20 ) 2 — e sinv = 0.

2 r ³ J               ⁰ r ³

zz

Тогда

A - -arcsin

°' 2

4       J zz

--e =i nv при

3 ' Jy J J    )

условии sinν ≤

3 ( J_yy– J_xx )

4     J_zze

Далее будем рассматривать участок траектории в окрестности перигея, где выполняется условие

4 J

--esinv

3 <  J yy J

< 1.

Для каналов крена и рыскания законы

управления ориентацией и разгрузкой в соответствии с работой [10] имеют вид:

ui = K i x. + [ K i ! - E r ]

A i   B i

N _i   0

M

-0 "З^ , y , (7)

где E _r — единичная матрица, а N _i = (1 1 1 1).

Таким образом, системы уравнений для каналов крена, рыскания и тангажа на участке

траектории, где выполняется условие (6), имеют вид:

x ^. i = ( A _i + B _i K _i ) x _i , i = x , y , z, (8) где К KvK-K^K 4 ).

Для обеспечения асимптотической устойчивости линейной динамической системы с постоянными коэффициентами необходимо и достаточно, чтобы спектр собственных значений замкнутой системы лежал в левой полуплоскости комплексной плоскости. В данной работе матрицы A _i систем управлений имеют периодические коэффициенты, а матрицы замкнутых систем A _i + B _i K _i являются матрицами с переменными коэффициентами. В этом случае для обеспечения устойчивости решений систем (8) в работе применялась теорема об асимптотической устойчивости линейной системы с переменными коэффициентами [11].

Для того чтобы применить эту теорему к системам (8), перепишем матрицу системы для каждого канала управления в виде суммы двух матриц: с постоянными A _пост и переменными коэффициентами C _i ( t ):

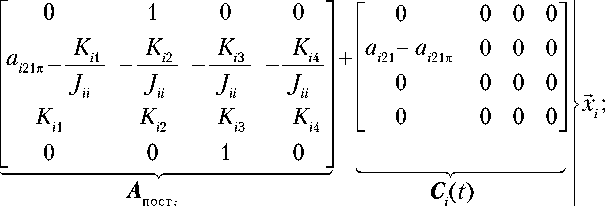
ββ

β i 3

K - J a^ + в 1 + „   ; K - j e n + ^i- ; K i1 ii    i21π       i1      a               i2 ii    i0      a               i3

i 21 π                                  i 21 π

β _{i 2}

a- 2i n ' ^{K 4}

a^

i 21 π

в i о = -( f о + f i + f 2 + f 3 );

в i 1 = f 0 f 1 + f 0 f 2 + f 0 f 3 + f 1 f 2 + f 1 f з + f 2 f i 3 ;

в i 2 = -( f 0 f 1 f 2 + f 0 f 1 f 3 + f 0 f 2 f 3 + f 1 f 2 f з ); в i 3 = f 0 f 1 f 2 f 3 *

Здесь K_ij — элементы матрицы регуляторов по состоянию в соответствующем канале управления, вычисленные по формулам метода точного размещения полюсов [12], суть которого заключается в том, чтобы заменить спектр значений замкнутой системы на желаемый спектр; f_j — в соответствии с методом точного размещения полюсов, собственные числа матрицы A _пост (корни характеристического полинома); в _{i 0}, P i 1 , в i ₂, в i ₃ определяются по формулам, которые выражают коэффициенты многочлена через его корни (формулы Виета); a_{i 21π} — значение элемента а. ₂₁ в перигее (при v = 0°); i = x , y , z ; j = 1, 2, 3, 4.

Из доказательства теоремы вытекает сле- дующий критерий:

4 c 1 i < min Re f^ ’ где c1i — константа, ограничивающая норму матрицы Ci(t) и зависящая только от Aпост ; i = x, y, z. i

В качестве эталонного многочлена, расположение корней которого и является желаемым при замыкании системы с постоянной матрицей A _пост , выбирался полином Баттерворта четвертого порядка, т. е.

min Re f..

ij

/ A π

Таким образом, для соответствующего канала управления р₀ i — радиус полуокружности в левой полуплоскости с центром в начале координат, на которой лежат корни эталонного многочлена, определяется из условия:

4 c

Р оГ

1 i

sin

π

Определим значение константы c _{1 z} для канала тангажа.

Под нормой матрицы C _i ( t ) понимается следующее:

II Ci' s 'll

a z 21    a z 21 π

—

a z 21

a_{z 21}π ;

I a z 21     a z 21 n

3G r 3 π

c 1 z

3 G r ³

II

3 G

2 —

π

cos(20O)

J yy – J xx J zz

G ( J y ^— J xx

⁶ r 3

n k

Jzz

| ;

где r _п — радиус-вектор центра масс КА относительно центра Земли в перигее.

Тогда

ρ_{0 z} >

π1111 "8

G r 3 π

(J yy

^- J x

I J z  V

Действуя аналогичным образом, получим оценки радиусов р₀ x и р₀ y для каналов крена и рыскания, соответственно:

ρ 0 x ^>

8(4 + e )

< J - J ^ ^G yy zz

π sin 8

3 J

π xx

результаты моделирования

Математическое моделирование проводилось в среде MATLAB при следующих условиях:

• •    начальные значения по кинетическому моменту по всем трем каналам управления принимались равными 10 Нмс;

• •    моделирование проводилось на участке орбиты, где значение истинной аномалии удовлетворяло условию (6);

• •    значения радиусов полуокружностей, на которых лежат собственные значения постоянных матриц А _пост для соответствующих каналов управления, выбирались, исходя из ограничений (9–11).

• •    значения углов отклонения ССК от ОСК по каналам крена и рыскания не превышали 20°, так как система уравнений (3) была получена в предположении малости этих углов. В то же время на угол отклонения в канале тангажа 6 это ограничение не накладывалось.

Численным методом определялось значение радиуса окружности по каждому каналу управления, исходя из ограничений (9–11), соответственно. Из всех возможных вариантов значения радиуса окружности в соответствующем канале управления выбиралось такое, при котором приращение кинетического момента было максимально при соблюдении ограничений в 20° на величину углов отклонения ССК от ОСК по каналам крена и рыскания.

Поиск управления по всем трем каналам осуществлялся с использованием выражения (7), в котором в качестве элементов матрицы М в каналах крена и рыскания брались элементы этих матриц на предыдущем вычислительном шаге. Моделирование объекта управления осуществлялось с использованием динамических уравнений Эйлера (2) и кинематических соотношений в кватернионной форме (1).

Ниже представлены графические результаты моделирования. На рис. 3–5 для каналов крена, рыскания и тангажа представлено по два графика, на верхних — изменение угла отклонения в соответствующем канале в градусах, на нижних — изменение кинетического момента в Нмс по соответствующей оси.

Из рис. 3–5 видно, что кинетический момент КА на участке орбиты в окрестности перигея разгружается, причем по каналам крена и тангажа кинетический момент разгружается полностью. При этом углы отклонения ССК от ОСК по каналам крена и рыскания не превышают 20°.

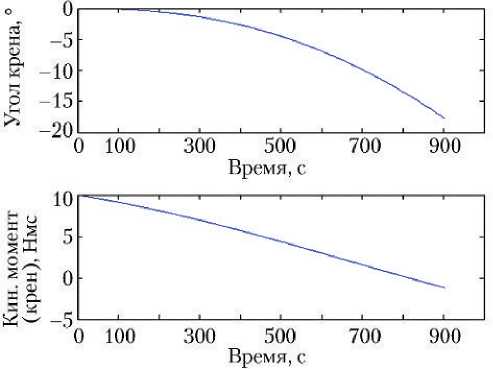
Рис. 3. Изменение кинетического момента инерционных исполнительных органов и угол отклонения в канале крена

орбите. Получены численные решения задачи управления ориентацией и разгрузкой кинетического момента КА на высокоэллиптической орбите по всем трем каналам на участке орбиты в окрестности перигея.