Управление отоплением зданий при низкотемпературных режимах теплоснабжения

Проблемам регулирования нагрузки систем теплоснабжения, построению графиков отпуска теплоты посвящено достаточно много работ [1–8]. Получены весьма важные и интересные для теории и практики результаты. Вместе с тем имеются и нерешенные вопросы, в частности, известна следующая подлежащая решению задача.

Энергоснабжающие организации, часто заметно снижая температуру теплоносителя в подающих магистралях тепловых сетей и нарушая, тем самым графики качественного регулирования отпуска теплоты [1–5], требуют от потребителей 100%-ной оплаты услуг теплоснабжения. Обосновывается последнее тем, что потребное количество теплоты якобы доставляется «расходом», однако при этом, как правило, не разъясняется, как и каким образом конкретно решается эта задача. В связи с этим весьма актуальным является вопрос о том, как следует изменять расход теплоносителя при существенном снижении его температуры с тем, чтобы задача теплоснабжения решалась должным образом, причем с помощью имеющегося оборудования. В данной работе рассматривается решение этой задачи.

Первый вариант решения задачи. Пусть требуется найти такой расход теплоносителя, при котором поток теплоты у потребителя (количество теплоты, переносимое через поперечное сечение теплопровода в единицу времени) будет одним и тем же, как при температуре теплоносителя t, так и при его температуре (t + At).

Нетрудно видеть, что для этого должно выполняться следующее соотношение:

G • t = (G + AG) • (t + At) ,                      (1)

где G - массовый расход теплоносителя, а AG -его приращение. Поэтому новый расход должен вычисляться по формуле

(G + A G) = G ^ t = G¹---

(t + A t)     (1 +A t/t)

.

Далее заметим, что из соотношения (2) следу-AG ет, что относительное изменение расхода и обуславливающее его относительное изменение At к температуры теплоносителя будут связаны уравнением

Δ G      Δ t/t

---=-- .

G     (1 +Δ t/t)

Анализируя знаменатель формулы (3), несложно заметить, что при отрицательном значении Δt

(температура теплоносителя снижается) его предельное значение будет равно –1, это когда температура теплоносителя якобы будет снижена до 0 °С и Δt=-t . Поэтому предельное значение относительного изменения расхода будет равно ΔG lim = ∞ , т. е. расход теплоносителя должен t →-1

быть увеличен до ∞ . Конечно, в реальных условиях температура теплоносителя может быть снижена только до определенного зависящего от технологических условий значения.

На рис. 1 приведен график зависимости (3) в процентном исчислении.

Как видно из рис. 1, при увеличении температуры теплоносителя его расход должен быть снижен, в частности, при 100%-ном увеличении – на 50 %. Наоборот, при уменьшении температуры прямой воды ее расход необходимо повышать. При этом следует иметь в виду, что новый расход (G + ΔG) в общем случае является функцией тем пературы наружного воздуха t Н , так как температура теплоносителя t в формуле (2) зависит от t Н , т. е. численное значение t определяется известным образом по температурным графикам теплоснабжения [1–5]. Поэтому в общем случае при разных температурах наружного воздуха t Н потребуется разное приращение расхода теплоноси- теля ΔG . Только если   = const во всем диапазо- t не изменения наружных температур, то будет и ΔG = const , если, конечно, при этом в исходном режиме применялось качественное регулирование отпуска теплоты, т. е. расход теплоносителя в любом случае был постоянным.

Второй вариант решения задачи. Постановка первого варианта задачи достаточно идеализирована, в частности, не учитывается существующее на практике ограничение на температуру обратной воды, например, всем известно, что недопустимо замерзание теплоносителя в теплопроводе. Поэтому решим ту же задачу, но только при условии, что температура обратной воды t ОБР = const при любом режиме теплоснабжения и равна при этом своему минимально допустимому значению. Такое требование, как известно, способствует повышению экономичности работы систем теплоснабжения. В этом случае должно вы- полняться следующее соотношение:

G(t-tОБР) =(G +ΔG) ⋅(t+Δt -tОБР) .      (4)

В связи с этим новый расход должен вычисляться по формуле

(G +Δ G) = G ⋅

1 - t_ОБР /t (1 +Δ t/t - t_ОБР /t) ^.

Нетрудно видеть, что в данном случае должно быть (tОБР - t)≤ Δt≤0 , поэтому предельное значе- ние Δt равно (tОБР - t) . Вследствие этого из формулы (5), в частности, следует, что при Δt→ (tОБР - t) (G +ΔG)→ ∞ , данный результат согласуется с простыми физическими соображениями. В самом деле, в этом предельном случае температура воды как в подающем, так и в обратном теплопроводах должна быть практически од-

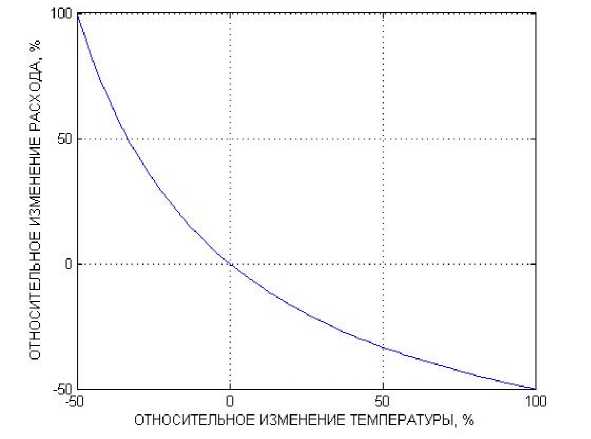
Рис. 1. Зависимость относительного изменения расхода теплоносителя от относительного изменения его температуры

ной и той же и равной t ОБР = const, т. е. съем теп- лоты с теплоносителя стремится к нулю, а поэтому его расход должен стремиться к да .

Из (5) следует, что формула для относитель-

AG г       _ ного изменения расхода будет иметь вид

AG =      - A1 /1

"g = (1 +A 1/1 - 1_ОБР /1) .

График данной зависимости для t = 150 ° C и

1_ОБР = 30 ° C приведен на рис. 2.

Из рис. 1, 2 видно, что при прочих равных условиях ограничение на температуру обратной воды приводит к необходимости увеличения расхода теплоносителя на большую величину, чем при отсутствии такого ограничения.

Третий вариант решения задачи. При управлении отоплением зданий в первую очередь важно, чтобы теплообменное оборудование потребителя «сняло» с теплоносителя нужное по погоде количество теплоты. Только при таком условии в здании будет поддерживаться требуемая температура внутреннего воздуха. Поэтому выясним, как должен изменяться расход теплоносителя в данной постановке, при этом систему отопления потребителя, как это уже принято, будем представлять эквивалентным отопительным прибором [4, 5, 9–11].

Таким образом, будем искать для новой температуры теплоносителя (t + At) новый расход

(G + AG), исходя из следующего соотношения [4,

• 5,    12]:

kF(1- 1в) =   kF(1+A1 - 1в)

1 + kF / (2cG) 1 + kF /[2c(G + A G)] ’

где t_В – температура внутреннего воздуха объекта теплоснабжения, kF – произведение коэффициента теплопередачи на площадь поверхности теплообмена эквивалентного отопительного прибора [4, 5, 9–11], c – удельная теплоемкость теплоносителя.

Соотношение (7) означает, что тепловой поток эквивалентного отопительного прибора как при прежнем расходе теплоносителя и при прежней его температуре, так и при новом расходе теплоносителя и при новой его температуре должен быть одним и тем же.

Выполнив некоторые преобразования, получим, что

• (G + A G) =        kW -Js)------ .      (8)

2c A 1 + kF(t + A 1 - 1_B)/G

При этом формула для относительного изме-AG нения расхода будет иметь вид

A G =      -A 1/1 - (kF) / (2cG) -A 1 /1

G =A 1/1 + (kF) / (2cG) ■ (1 + A 1/1 - t_B /1) ^. ( )

Формула (8) указывает, каким должен быть новый расход теплоносителя (G + AG) при снижении его температуры t на величину A t.

По условию физической реализуемости из соотношения (7) следует, что поскольку при низкотемпературном теплоснабжении A t <  0, то должно быть A G >  0 . Числитель формулы (9) величина положительная, поэтому ее знаменатель тоже должен быть положительной величиной, т. е.

At/t + (kF)/(2cG) ■ (1 + At/t - tB/t) > 0.    (10)

Отсюда получаем, что при снижении темпе-

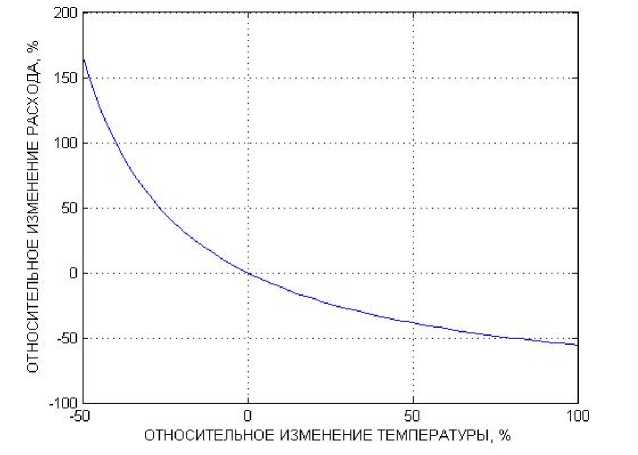
Рис. 2. Зависимость относительного изменения расхода теплоносителя от относительного изменения его температуры при постоянной температуре обратной воды

ратуры теплоносителя величина At должна удов- летворять следующему неравенству [12]:

At >-    (t-^)    .                  (11)

[ 1 + (2cG)/(kF) ]

Таким образом, потребное количество теплоты можно «снять» с теплоносителя только в том случае, если выполняется неравенство (11). При этом отметим, что если At будет равно величине, указанной в правой части неравенства (11), то функция (9) будет иметь разрыв 2-го рода, по-

AG             А           (t — t )

скольку-->^ при At^-        В + 0.

G                     [ 1 + (2cG)/(kF) ]

Слева от точки разрыва формулами (8) и (9) по условию физической реализуемости пользоваться нельзя.

На рис. 3 приведен график зависимости, указанной формулой (9), для t = 150 ° C, t_B = 18 ° C и (kF)/(2cG) = 0,1938. В этом случае должно быть A t >- 21,43 ° С.

Как видно из рис. 3, снижение температуры теплоносителя в данном случае требует весьма существенного увеличения его расхода, так, например, при снижении температуры всего лишь на 10 ° C расход теплоносителя должен быть увеличен более, чем на 87 % . Только в этом случае потребитель с его теплоиспользующим оборудованием получит должное количество теплоты.

Если обозначить температуру обратной воды для первого режима теплоснабжения как tОБР 1 , а для второго режима как tОБР2 , то нетрудно видеть, что должно выполняться следующее соотношение:

^G ' ^(t - ¹ ОБР1 ⁾ = ^{(G + A G)} • ^{(t + A t} - ¹ ОБР2 ⁾ . ⁽¹²⁾

Из данной формулы следует, что

⁽t + ^A t ^- 1₀ Бр2 ) = — —• ⁽t ^- 1₀ Бр1 ).         ⁽13)

G + AG

G

Так как в данном случае ------ < 1, то из со-

G + AG отношения (13) вытекает, что (t + At - 1ОБР2) < (t - 1ОБР1), т. е. уменьшение температуры теплоносителя обуславливает как увеличение его расхода, так и снижение разности температур прямой и обратной воды.

Из формулы (12) следует, что

^БР2 = ^{(t + At) -} Т; 77Г" ^{(t -} t OBP1 )-        ⁽¹⁴⁾

G + AG

Поэтому

^БР1 ^БР2 =

AG

• ⁽¹ ОБР1 ^- 0^{-A t} . G + A G

Так как (1_ОБР1 -1) < 0 и A t <  0 при низкотемпературном теплоснабжении, то из (15) следует, что (1_ОБР1 - 1_ОБР2) может быть как больше, так и меньше ноля, т. е. температура обратной воды во втором – низкотемпературном режиме может быть как больше, так и меньше температуры обратной воды в первом (базовом) режиме теплоснабжения.

Известно, что мощность теплообменного оборудования (тепловой поток) абонента можно описать и следующей формулой [4, 5, 9–11]:

kF(t _ОБР1 –t _В )     kF(t _ОБР2–t_В)

W=       =          .

АБ 1– kF/(2cG) 1–kF/[2c(G+ΔG)]

Причем также известно, что в рабочем диапазоне (kF) / (2cG) <1, поэтому оба знаменателя в соотношении (16) положительны, следовательно (учитывая, что WАБ > 0), в обоих режимах

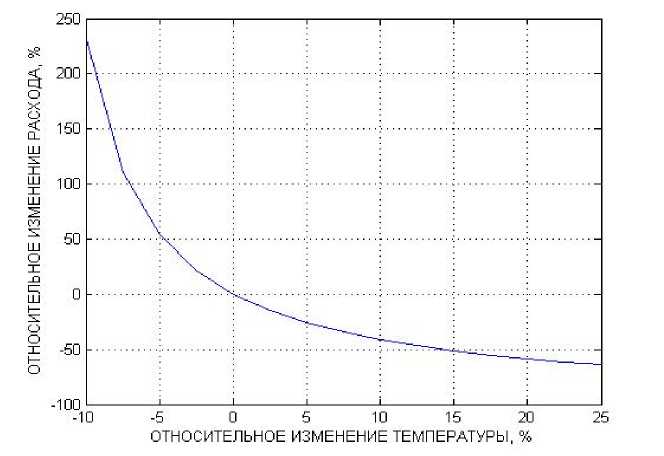
Рис. 3. Зависимость относительного изменения расхода теплоносителя от относительного изменения его температуры при учете характеристик теплообменного оборудования потребителя

tОБР1 > tB и tОБР2 > tB , что согласуется с простыми физическими рассуждениями, а поэтому подтверждает справедливость и физическую реализуемость вышеприведенных результатов.

Четвертый вариант решения задачи. Неравенство (11) определяет предельное значение A t, при котором с теплоносителя расходом еще можно «снять» требуемое количество теплоты. Это значение невелико, например, при t = 150 °C , t_B=18°C и (kF)/(2cG) = 0,1938 должно быть Δt>–21,43 °С . Практика, как правило, допускает возможность некоторого ухудшения качества теплоснабжения [13–15], т. е. некоторого уменьшения количества доставляемой теплоты по сравнению с тем, что требуется по погоде. Понятно, что это вызывает некоторое снижение температуры внутреннего воздуха зданий. Поэтому будем считать, что при низкотемпературном теплоснабжении потребляемая теплота может составлять определенную долю ф от теплоты базового режима, понятно, что 0 <ф< 1.

В связи с этим будем искать новый расход (G + AG) для новой температуры теплоносителя (t + At) , исходя из следующего соотношения:

. kF(t - 1 в ) =    kF(t +A t - 1 в )        ₍₁7)

^ф 1 + kF/(2cG) 1 + kF/[2c(G + A G)]’   ¹ ’

Выполнив некоторые преобразования, получим, что

(G + AG) =

______________фkF(t- tB)_____________ kF                              . (18)

2c[(1 + ^) ■ (t + A t - t B ) -Ф- (t - t B )]

2cG

При этом величина A t должна удовлетворять следующему неравенству:

(t - t B ) ■ [1 + (2сG)/(kF) ■ (1 -Ф)] [ 1 + (2сG)/(kF) ]

Сравнивая неравенства (11) и (19), заключаем, что предельное значение A t увеличилось, в частности, для t = 150 °C , t_В = 18 °C , (kF) / (2cG) = 0,1938 и ф= 0,8 должно быть Δt>–43,55°С.

В данном случае в правой и левой частях уравнения (17) использовалось одно и то же значение tВ . Таким образом, в данном варианте решения задачи теплоснабжения считалось, что некоторое снижение температуры внутреннего воздуха, которое будет иметь место, мало влияет на получаемый ответ. В самом деле, вряд ли можно ожидать, что величина (t+At - tB) изменится достаточно существенно из-за уменьшения tВ [14]. Более того, необходимо иметь в виду, что из-за снижения tВ действительное значение этой величины будет несколько больше принимаемого в формуле (17) значения, поэтому фактическая теплоотдача системы отопления тоже будет чуть выше, чем это предполагается при решении задачи.

Тем не менее, если решать данный вариант задачи достаточно скрупулезно, то можно определить, что новую – сниженную температуру внутреннего воздуха tВН можно вычислить по уравнению tH = t +ф. kF(t- tB) ■ '

^{B H Ф} 1 + kF/(2cG) q V V,

где qV – усредненная удельная тепловая характеристика зданий района, V – их общий объем, t Н – температура наружного воздуха. Новый расход при этом следует вычислять по уравнению

(G + aG) = фkF(t- tB)

kF                         kF

^{2c[(1 +} ytt) ■ ^{(t +A t -} t H ) ^{-ф (t -} t B ) ■ ⁽¹⁺— ,;)]

2cG                    qVV

. (21)

Таким образом, подчеркнем, что допустимый диапазон снижения температуры теплоносителя, при котором потребителю в точности доставляется требуемое по погоде количество теплоты ( t базового режима является функцией температуры наружного воздуха t _H), весьма ограничен. Если A t снижается на большую величину, то имеет место снижение качества теплоснабжения – потребителю может быть доставлено только меньшее количество теплоты.

Кроме того, заметим также, что эквивалентным отопительным прибором допустимо представлять не только отдельное здание, но и целый микрорайон теплоснабжения [14].

Выводы

Приведены решения четырех вариантов задачи управления расходом теплоносителя при снижении его температуры в подающей магистрали. Установлено, что допустимый диапазон снижения температуры теплоносителя, при котором потребителю в точности доставляется требуемое по погоде количество теплоты, достаточно ограничен. Показано, что этот диапазон зависит от температуры наружного воздуха, так как температура теплоносителя в базовом режиме зависит от этой величины. Если температура снижается на большую величину, то имеет место уменьшение качества теплоснабжения, потребителю может быть доставлено только меньшее количество теплоты – доля от теплоты базового режима.