Управление отжигом стальных рулонов в колпаковых печах

Системы автоматизации колпаковых печей, широко применяемых в металлургической отрасли для термообработки металла, характеризуются довольно продолжительной историей своего развития, однако есть еще много задач, требующих улучшения своего решения [1–8]. Поэтому проблема совершенствования таких систем является, безусловно, актуальной. Здесь к месту следует отметить, что даже относительно небольшой успех в решении задач контроля и управления процессом термообработки в силу достаточно больших масштабов производства приводит к существенной экономии топлива или электроэнергии, к повышению производительности и качества готовой продукции [1–8].

Как известно [5], системы управления температурным режимом колпаковых печей, определяющие в значительной мере эффективность функционирования печей и качество термической обработки металла, в своем развитии прошли несколько ступеней (этапов). Как правило, выделяются следующие основные ступени развития [9–11]:

• 1)    ручное управление (в том числе дистанционное управление исполнительными механизмами);

• 2)    применение обычных систем автоматического регулирования (САР) температуры, причем, как правило, двухпозиционных;

• 3)    системы программного управления;

• 4)    системы управления с обратной связью по температуре садки.

Дополнительно можно отметить адаптивную систему стабилизации температуры колпаковой термопары в период нагрева и стендовой термопары в период выдержки, внедренную в свое время на ПАО «Новолипецкий металлургический комбинат» [12–14].

Системы ручного управления

Системы ручного управления обеспечивали требуемый нагрев металла в той мере, в какой это позволяли опыт и интуиция обслуживающего персонала. Адаптация к изменяющимся условиям работы печей осуществлялась редко и в очень ограниченном объеме [11]. Здесь использовалось дистанционное управление исполнительными механизмами и устройствами, при этом контролировалась степень открытия регулирующих органов на газопроводах топливных печей (по дистанционным указателям положения) или напряжение на нагревателях электрических печей сопротивления.

Системы автоматическогорегулирования

Внедрение САР температуры следует считать шагом вперед по сравнению с системами ручного управления, так как регуляторы автоматически вычисляли расход топлива или электроэнергии, требуемый для обеспечения заданной температуры в представительной точке системы «печь – садка».

В настоящее время колпаковые печи в большинстве случаев оснащены САР двухпозиционного типа. Качество регулирования двухпозиционными САР следует признать достаточно низким, это отрицательно сказывается на качестве готовой продукции. Так, по данным работы [14] точность стабилизации температуры греющей среды двухпозиционными САР составляет на этапе нагрева ± 25 °C, а на этапе выдержки ± 100 °C, точность стабилизации температуры защитного газа ± 8 °C. Кроме того, автоколебательный режим работы применяемых САР снижает срок службы электрических нагревателей или исполнительных механизмов топливных пе- чей, а также и огнеупорной кладки вследствие большого количества теплосмен. Поэтому целесообразны разработка и внедрение более эффективных САР. Именно по этой причине была разработана и внедрена адаптивная система [12–14], которая обеспечила точность стабилизации температуры греющей среды на уровне ± 12 °C на протяжении всего отжига, точность стабилизации температуры защитного газа при этом составила ± 3 °C.

Для колпаковых электропечей сопротивления с двумя зонными нагревателями может быть рекомендована САР непрерывного типа , предложенная в работах [15, 16]. Здесь необходимо решать задачу управления двумя нагревателями по сигналам от трех термопар: двух зонных колпаковых и одной стендовой [15, 16]. Точность поддержания температур при этом существенно повышается, исключаются частые теплосмены зон печи и не допускается перегрев зон колпака и садки.

Здесь следует иметь в виду следующее [16]. Если в двухзонных (многозонных) колпаковых печах регулируется только температура зон (термопары установлены в зонах печи), то наблюдается низкая точность регулирования температуры отжигаемого металла. Объясняется это тем, что между температурой зон и температурой металла не существует однозначной зависимости – температура металла (садки) помимо температуры зон зависит еще и от массы и габаритов садки, радиальной и аксиальной теплопроводности рулонов и т. д.

Устройство [16] содержит ПИ-регуляторы (пропорционально-интегральные регуляторы) температуры отдельных зон печи и ПИ-регулятор температуры стендовой термопары (отжигаемого металла). В системе управления сравниваются выходные сигналы каждого из зонных регуляторов с выходом регулятора температуры металла и на соответствующий зонный нагреватель (его пропорциональный исполнительный элемент) пропускается только меньший из двух сигналов. Тем самым обеспечивается повышение точности поддержания нужной температуры металла и исключаются перегревы элементов печи.

В работе [6], к сожалению, регулируется только температура зон двухзонной колпаковой печи. Тем не менее все-таки можно утверждать, что разделение электрических нагревателей или газовых горелок печи на несколько зон положительно сказывается как на точности поддержания температурного режима, так и на качестве готовой продукции, а также и продолжительности службы конструктивных элементов печей.

Недостатки систем управления первого и второго типов известны и практически те же, что и в случае нагревательных печей [17, 18]. Однако при этом в случае колпаковых печей, как правило, нет необходимости в согласовании их производительности с ритмом работы какого-либо другого технологического оборудования. Это существенно упрощает задачу управления печами.

Автоматические системы программного управления отжигом

При оснащении колпаковых печей системами управления первого и второго типов реализация многоступенчатой технологии термообработки осуществляется вручную обслуживающим персоналом. Системы программного управления предназначены для автоматической реализации сложной многоступенчатой технологии термообработки и этим выгодно отличаются от систем первого и второго типов [6, 7]. При этом к месту следует заметить, что в случае применения развитых систем программного управления, реализованных на базе современных микропроцессорных средств, может быть получено значительное увеличение производительности без снижения качества термообработки металла. Дело в том, что анализ технологической документации на отжиг показал [15], что продолжительности периодов нагрева и выдержки, а также времени охлаждения металла на стенде заданы в виде ступенчатых функций массы садки, т. е. для любого значения массы садки, принадлежащего определенному интервалу, продолжительность периода термообработки будет одна и та же. Вместе с тем очевидно, что длительность этих стадий должна изменяться непрерывно при изменении массы садки. Ступенчатая аппроксимация этих зависимостей, используемая на практике, обусловлена физическими возможностями технологического персонала, реализацией многоступенчатой технологии отжига вручную. Автоматическая реализация технологического процесса позволит перейти к реализации продолжительности периодов нагрева, выдержки и охлаждения в виде непрерывных функций массы садки , что повышает производительность печей, например, для условий

ОАО «Магнитогорский калибровочный завод» (МКЗ) производительность в свое время была повышена до 6 %, по этой причине наблюдалось и снижение расхода электроэнергии на отжиг. Увеличение производительности объясняется тем, что при составлении технологических инструкций на отжиг без программных систем управления аппроксимация непрерывной зависимости производится «описанной» ступенчатой фигурой (функцией) , «…задается с запасом в расчете на наиболее неблагоприятные условия протекания процесса» [19].

Системы управления с обратной связью по температуре садки

Так же, как и в случае нагревательных печей, наиболее перспективными являются системы управления, реализующие принцип обратной связи по температуре садки [17, 18]. В противном случае отжиг ведут, практически не контролируя температурное поле садки, а о завершении периодов (стадий) термообработки судят по их временной длительности, причем необходимое время нагрева и выдержки металла определяют эмпирически в процессе отработки технологии и фиксируют его в технологической инструкции.

Недостатками такого способа управления являются либо низкое качество термообработки металла, либо неоправданно заниженная (с точки зрения обеспечения заданного качества термообработки) производительность печей, если реально необходимое время термообработки данной садки в данной печи отличается от заданного в технологической инструкции.

Отмеченные недостатки обусловлены тем, что с течением времени изменяются теплотехнические характеристики печей, а теплофизические свойства термообрабатываемых садок не являются постоянными, т. е. вследствие того, что в теплотехническом отношении каждая система «печь – садка» представляет собой сугубо индивидуальный объект. Поэтому время полного цикла термообработки и ее отдельных периодов, реально необходимые для достижения заданного качества термообработки металла, будут изменяться, эти величины будут либо больше, либо меньше значений, указанных в технологической инструкции.

Если время термообработки данной садки, реально необходимое для достижения за- данного качества металла, будет больше установленного технологической инструкцией, то процесс закончится при повышенном перепаде температур в садке, а следовательно, при низком качестве отжига металла. В противном случае длительность цикла термообработки будет неоправданно большой и, как следствие, низка производительность печей.

Данные недостатки устраняются с помощью систем управления с обратной связью по температуре металла, определяемой по адаптивным математическим моделям, так как инструментальный контроль температуры возможен лишь в ограниченном числе точек, доставляет достаточно серьезные трудности и не всегда целесообразен. Так, например, в колпаковых печах ПАО «Магнитогорский металлургический комбинат» (ММК) температура металла измеряется двумя термопарами: верхняя термопара закладывается за 5–6-й наружные витки верхнего рулона стопы, а рабочий спай нижней термопары прижимается к торцу нижнего рулона [20]. Температура продуктов сгорания между колпаком и муфелем контролируется с помощью зональной термопары. Следует отметить, что используются и другие точки контроля температурного режима печей [9, 21, 22].

Вполне понятно, что в системах управления с обратной связью по температуре отжигаемого металла предъявляются особые требования к математическим моделям процесса, к точности и надежности расчетов на их основе, в целом к алгоритмическому обеспечению систем. Как отмечено в [23], математические модели являются в настоящее время основным элементом «ноу-хау» при автоматизации.

К математическим моделям, являющимся ядром алгоритмического обеспечения систем управления с обратной связью по температуре металла, предъявляются следующие требования [17, 18]. Во-первых, математические модели должны обеспечить хорошую точность расчета температурного поля отжигаемых рулонов, так как от этого зависит величина эффекта от применения систем. Во-вторых, системы управления должны работать в реальном масштабе времени, т. е. длительность цикла расчетов в УВМ должна быть достаточно малой и должна удовлетворять требованиям к качеству процесса управления (быстродействие расчетов). В-третьих, математические модели должны быть «привязаны» к штатным или разумным средствам измерения параметров процесса нагрева. Последнее относится как к средствам измерения, сигналы которых используются при расчете температурного поля металла, так и к средствам, необходимым для идентификации (настройки) моделей на реальный процесс.

Точность и быстродействие расчетов прямо связаны со структурой математической модели процесса нагрева, структура модели определяет также и необходимые средства измерения параметров процесса нагрева, поэтому выбор структуры модели является наиболее важным.

Обычно в контуре управления печами применяются упрощенные модели нагрева металла, которые не всегда полностью настраиваются на реальный процесс в течение текущего отжига [24–31]. Так, по данным работы [24] за рубежом есть примеры использования в контуре управления простой математической модели, связывающей температуру греющей среды с температурой экстремальной точки садки. Применяются также и простые экспоненциальные и регрессионные модели [24, 26, 32–34]. Модели, учитывающие в достаточной мере механизмы теплофизических явлений при отжиге, требующие выполнения большого объема вычислений, обычно не используются в контуре управления отжигом, такие модели применяются либо для настройки алгоритмов контроля и управления, осуществляемой вне контура управления, либо для разработки технологических инструкций.

Как правило, в процедурах адаптации моделей используются экспериментальные данные по термообработке предыдущих садок или же задача параметрической идентификации моделей решается по данным специально подготовленных экспериментальных отжигов [6, 24–31]. Поэтому целесообразна разработка способов идентификации моделей процесса термообработки, реализуемых полностью по информации, получаемой только в процессе текущего отжига. Здесь может быть рекомендован способ [5, 15, 17, 35], требующий измерения в процессе текущего отжига температуры металла в трех различных по радиусу точках основания нижнего рулона с помощью так называемых прижимных термопар. Такое расширение существующих систем контроля температурного режима колпаковых печей является достаточно приемлемым.

Алгоритм температурного контроля в процессе выдержки

Как известно [17] в регулярном тепловом режиме температура любой точки тела произвольной формы удовлетворяет уравнению t (Mi ,т) = tп + A • U (Mi )• exp (-ц-т), (1) где t (Mi, т) - температура в точке Mi в момент времени τ , tп – температура рабочего пространства печи, при которой осуществляется выдержка металла, U (Mi) - функция координат точки Mi , A – постоянная, не зависящая ни от координат, ни от времени, она определяется из начального температурного поля перед выдержкой, ц - некоторый постоянный коэффициент. Заметим также, что U (Mi) и ц зависят от теплотехнических характеристик системы «греющая среда – металл», а величины A и ц имеют одинаковое значение для любой точки тела [17].

Используя уравнение (1), с помощью несложных выкладок для произвольных точек M ₁ , M ₂ , M ₃ можно получить следующее соотношение:

t п - 1 ( M 1 , т ) = и ( M 1 )

t ( M 2 , т ) - 1 ( M 3 , т ) и ( M 2 ) - и ( M 3 ) ^.

Отсюда следует, что отношение разности температуры рабочего пространства и температуры некоторой точки M ₁ к разности температур каких-либо других точек M ₂ и M ₃ является постоянной во времени величиной, не зависящей также и от температурного поля тела в начале периода выдержки. Зависит это отношение, как это отмечено выше, от теплотехнических характеристик системы «греющая среда – металл» и от координат используемых точек. Поэтому, измерив одну из этих разностей, по соотношению (2) можно определить и другую.

В качестве точки M ₁ следует выбирать такую точку на поверхности, для которой наиболее просто измерить температуру. Координаты точек M ₂ и M ₃ при контроле наибольшего перепада должны соответствовать координатам точек с максимальной и минимальной температурами тела. При этом очень часто M 1 = M 2 , т. е. наиболее просто измерить температуру точки, лежащей на поверхности, которая к тому же является и точкой с максимальной температурой. В этом случае формулу (2) можно переписать в виде:

t П - 1 ( M 1 , т )    =      и ( M 1 )

t ( M 1 , т ) - 1 ( M 3 , т ) U ( M 1 ) - U ( M 3 ) .

Интересующий нас максимальный перепад температуры по сечению A t max = t ( M 1 , т ) - 1 ( M ₃, т ) будет равен

^A t m^aX = [ ¹ — UM)    t п — t ^{( M} 1 ’    .                                                    ⁽⁴⁾

К месту заметим, что данный метод контроля достаточно широко апробирован для случая нагрева слябов в методических печах стана «2500» ПАО ММК [17, 18].

Настройка алгоритма контроля

Понятно, что точка M 3 (точка с самой низкой температурой металла) находится внутри нижнего рулона, поэтому в процессе обычного отжига измерить температуру в этой точке и напрямую оценить завершение этапа выдержки не представляется возможным (или целесообразным). Из-за этого необходимо по более удобным для измерения температуры точкам определить необходимое количество величин A • U (Mi) и ц и по ним вычислить те плохо определяемые рас- четным путем параметры системы «греющая среда – металл», от которых зависит числовое значение U (M3).

Как это следует из [21], для случая отжига стальных рулонов в колпаковых печах уравнение (1) будет иметь следующий конкретный вид:

t ( r , z , т ) = t п + A •

J ₀

<

Y — + D • Y o

V R 2 7

/     7

r

V R 2 >

cos g — • exp ( -ц^т ) .

V S) ^{v 7}

Расчетная схема рулона приведена на рисунке. Здесь ai, i = 1,4 - коэффициенты теплоотда- чи, r и z – цилиндрические координаты точки, температура которой определяется, R1 и R2 – соответственно внутренний и внешний радиусы рулона, Xr - коэффициент радиальной тепло- проводности, 2S – его высота, начало координат находится в центре рулона, нагрев по высоте рулона считается симметричным, т. е. полагается, что a3 = a4 , J0, Y0 - соответственно функции

Бесселя первого и второго рода нулевого порядка от аргументов

r

^YT V R 1 7

и

r

V R 2 7

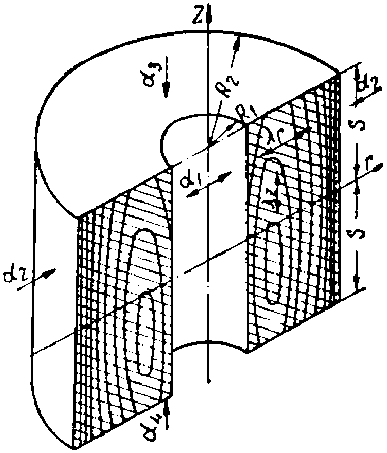
Расчетная схема рулона

Calculation scheme of the roll

В данном случае настраиваемыми параметрами являются A , у , D , а , причем к месту следует пояснить, что параметр ц является функцией у и о .

Такое количество настраиваемых параметров обуславливается тем, что трудноопределяемыми физическими параметрами являются коэффициенты теплоотдачи a i ,i = 1,4 и коэффициент радиальной теплопроводности X r , т. е. параметров пять. Однако из-за того, что достаточно обоснованно считается, что а ₃ = а ₄, определяемых параметров будет четыре. От этих коэффициентов и зависят собственно присутствующие в уравнении (5) параметры, которые подлежат идентификации.

Как известно, для определения 4 параметров нужно составить 4 уравнения. Поэтому при отжиге необходимо измерять температуру в трех различных точках, это дает необходимые 4 экспериментальных значения A • U ( M 1 ) , A • U ( M 2 ) , A • U ( M 3 ) и ц . Все это и позволяет замкнуть 4 уравнения для определения A , у, D и а . Понятно, что для настройки нужно выбирать наиболее удобные для измерений точки, для колпаковых печей, как это нам представляется, это три различные по радиусу точки основания нижнего рулона. Температура в этих точках измеряется с помощью прижимных термопар. Конечно, возможны и другие варианты размещения термометров.

Заметим, что справедливость уравнения (1) (или, что то же самое (5)) – справедливость применения закономерностей регулярного теплового режима – подтверждена, в частности, и экспериментальными исследованиями работы [32]. Кроме того, хорошо известно, что «…особенность термообработки – наличие ярко выраженного периода выдержки» [19, с. 406], что «.. .продолжительность каждой ступени достаточно велика, и время т удовлетворяет условиям, разрешающим применять приближенные формулы для определения температур металла, печи и теплового потока в любой ступени нагрева» [19, с. 407]. Эти данные также подтверждают обоснованность применения формулы (1) (закономерности регулярного режима нагрева).

По данным работ [33, 34], самая холодная (экстремальная) точка садки не имеет фиксированных координат, в процессе отжига она перемещается в радиальном направлении, интервал для ее координаты по радиусу, например, согласно [33], таков:

« 1 + 3 ( R 2 — R 1 ) ^ Г э ^ R 1 + 2 ( R 2 — R 1 ) , (6)

где r _э – радиальная координата экстремальной точки. Поэтому при наличии такой особенности процесса модели и алгоритмы контроля температуры, разработанные в предположении постоянства координат самой холодной точки садки, вряд ли способны обеспечить достаточную точность. В данном же случае после настройки уравнения (5) можно с достаточной точностью вычислить температуру любой, в том числе и экстремальной точки рулона, для этого следует просто задать ее координаты, этим, вне всякого сомнения, предлагаемое решение задачи выгодно отличается от известных в литературе [24–29]. Заметим, что, данное решение было реализовано в свое время в работе [15] для колпаковых печей цеха ленты ОАО МКЗ.

В работе [24] указано, что на печах фирмы Armco Steel Corporation штатно измеряется как температура защитного газа, так и температура основания нижнего рулона. Здесь также на основании решения уравнения теплопроводности и проведенных экспериментов, в которых дополнительно измерялась и температура экстремальной точки (половина высоты нижнего рулона и одна треть толщины нижнего рулона от его внутренней поверхности), установили, что взаимосвязь температуры любой точки рулона, в том числе и экстремальной, с температурой защитного газа последней выдержки может быть представлена динамической экспоненциальной моделью (это, вообще-то, тоже является экспериментальным подтверждением допустимости использования закономерностей регулярного режима). При исследовании также выяснили, что между параметрами модели для температуры экстремальной точки и такими же параметрами модели для температуры основания нижнего рулона существует достаточно достоверная регрессионная связь. Поэтому, определяя в процессе текущей выдержки параметры модели для измеряемой температуры основания, по регрессионной модели находят соответствующие параметры для экстремальной точки и по ее модели вычисляют температуру самой экстремальной точки. Объясняется такое различие в особенностях решений задачи контроля следующим.

Если структуру математической модели выбирать на основе физики процесса, то, как это следует из уравнения (5), ее настраиваемые параметры одинаковы для всех точек рулона, учитывать нужно только различные координаты точек. Поэтому различные для различных точек значения параметров настройки в модели фирмы Armco Steel Corporation объясняются ничем иным, как тем, что при синтезе структуры модели физические параметры, являющиеся const при конкретном отжиге, объединили с координатами точек.

Отметим, что достаточно интересным является способ определения конца отжига рулонов, предложенный в работе [36]. Здесь используется адаптивная модель изменения положения выходного вала исполнительного механизма, регулирующего расход топлива на отжиг. Утверждается, что изменение положения зависит от прогретости садки. Процесс считается законченным, когда относительное изменение положения становится достаточно малым. Однако, на наш взгляд, числовое значение условия окончания процесса для различных садок все-таки должно быть разным, так как, как уже отмечалось выше, теплофизические свойства садок достаточно индивидуальны.

Некоторые замечания по идентификации уравнения (1)

С целью упрощения решения задачи идентификации уравнение (1) следует записать в логарифмическом масштабе

ln [ t ( Mi,T)-tп ] = ln [ A • U ( Mi )]"^T                                                       (7)

Далее критерий идентификации целесообразно выбрать в виде интеграла по времени от квадрата невязки между левой и правой частями данного уравнения, когда в это уравнение подставлены экспериментальные данные

I ( A ■ U ( M i ) , ц ) = | 0 к [ ln ^[ t ^э( M i , t ) - t П ]- In ^[ A • U ( M i ) ] + цт] d t .                            (8)

Здесь t ^э ( M i , t ) и t П - измеренные значения температуры точки M i и температуры рабочего пространства печи соответственно, т _к - длительность процесса идентификации.

Вычисляя производные от данного критерия по d ln [ A ■ U ( M i ) ] и по 5ц и приравнивая их к нулю, найдем из полученной системы уравнений оптимальные значения параметров:

_ ^тк/ 2 J ^тк^{ы [} t э ( ^Mi , ^т ) ^- t п ] d ^т- ( 0 к ^т^ ^{ln [} t ^э ( ^Mi , ^т ) ^- t п ] d ^{т ц}=                                        2                                 ,

ln[ A ■ и (Mi )] = -2 J V ln[ tэ (Mi, г)—tп] d т+2 pv (10) Тк 3

Можно, конечно, решать задачу идентификации уравнения (5) и по измерениям температуры только в одной точке рулона подобно тому, как это делалось для многопараметрической модели методической печи только по экспериментальной температуре слябов на ее выходе [17, 18]. Однако при измерениях в одной точке нет никакой вариабельности режимов термообработки – текущий режим отжига такой, какой он есть. Вариабельность экспериментальных режимов нагрева, как показал опыт решения подобной задачи для методических печей [17, 18], весьма существенна, практически невозможно настроить модель по результатам нагрева одиночного сляба или группы слябов с одними и теми же количественными данными процесса в печи [37]. Могут быть получены весьма неправдоподобные сочетания числовых значений настраиваемых параметров, дающие одинаково приемлемые значения критерия идентификации. При этом также следует учесть, что все необходимые процедуры – и настройку модели, и контроль с ее помощью температуры экстремальной точки – нужно достаточно оперативно решать во время текущего отжига. Несомненно, что при измерениях в одной точке длительность собственно этапа настройки будет больше, чем в случае трех точек, к тому же эта длительность может оказаться недопустимо большой, и вследствие этого реализация этапа контроля может оказаться совершенно бесполезной из-за завершения собственно всего процесса термообработки.

В целом необходимо подчеркнуть, что решение задачи как структурной, так и параметрической идентификации моделей термических печей требует своего дальнейшего развития, по существу, с точки зрения создания АСУ ТП проблемы алгоритмизации контроля и управления являются, к сожалению, малоразработанными. При этом, несмотря на возросшую производительность современных компьютеров, требование простоты математического описания, обеспечивающего удовлетворительную точность, является по-прежнему актуальным [9, 17, 22]. Поэтому целесообразны дальнейшие разработки в данном направлении, в частности, оправдано применение достаточно простых алгоритмов контроля температурных полей отжигаемых рулонов, основанных, в частности, на закономерностях регулярного теплового режима.

При решении задач параметрической идентификации моделей применяются различные критерии и алгоритмы обработки исходной информации, при этом состояние проблемы таково, что требуется разработка достаточно простых, помехоустойчивых и быстродействующих алгоритмов идентификации. Следует также отметить, что при решении задач настройки моделей «на реальный процесс», не удается создать подсистему идентификации, работающую полностью в автоматическом режиме, по-видимому, разумно ограничиться решением части задач на уровне человеко-машинных процедур, включающих, например, проведение периодических спе-

циально подготовленных измерений температуры металла в печи наиболее достоверными контактными методами [38].

В целом использование вышеотмеченных результатов позволит создать алгоритмическую основу для построения высокоэффективных систем управления температурным режимом колпаковых печей. По многочисленным оценкам это ведет к снижению расхода топлива или электроэнергии на 10–15 %, увеличению их производительности на 6–10 % и существенному повышению качества термообработки металла [9, 13, 22, 24], так, например, только внедрение системы [13] привело к увеличению выпуска металла высших категорий качества более чем на 25 %.

Выводы

Проведен анализ истории развития систем управления температурным режимом колпаковых печей. Для электропечей сопротивления с двумя зонными нагревателями и стендовой термопарой предложена САР непрерывного типа. Указан достаточно простой способ увеличения производительности печей за счет использования автоматических систем программного управления. Предложен вариант создания адаптивной математической модели для периода выдержки рулонов, позволяющей повысить точность определения момента окончания процесса. Рассмотрены вопросы создания современных интеллектуальных систем управления. Результаты работы могут быть использованы при построении АСУ ТП колпаковых печей.