Управление при развертывании тросовой системы на эллиптической орбите

тической орбиты, что позволяет уменьшить ошибки приведения КТС в заданное конечное состояние при работе системы регулирования выпуском троса.

В настоящей работе рассматривается КТС, состоящая из базового и малого космических аппаратов (КА). Предполагается, что масса базового КА, с которого осуществляется выпуск троса, много больше, чем массы малого КА и троса. Предлагается номинальная программа развертывания КТС на эллиптической орбите в вертикальное положение, обеспечивающая выпуск троса на заданную конечную длину. Рассматриваемая программа не требует решения краевой задачи о приведение системы в заданное состояние, так как конечное положение КТС обладает свойством асимптотической устойчивости.

Для определения программы развертывания КТС построена математическая модель движения КТС в орбитальной подвижной системе координат, учитывающая массу троса [13] и параметры эллиптической орбиты. Параметры программы управления выбираются из условия приведения КТС в заданное состояние. Программы управления предназначены для механизмов выпуска троса, работающих только на торможение и не втягивающих трос [2].

Проверка возможности использования предлагаемой программы и принятых допущений проводится с применением конечно элементной модели движения КТС, в которой трос представляется как дискретная совокупность материальных точек, связанных между собой упругими связями. Данная модель записана в геоцентрической системе координат, при этом предполагается, что на каждом элементарном участке сила натяжения подчиняется закону Гука. Сила в механизме управления представляет собой сумму двух составляющих: программной силы и поправок к управлению, которые вычисляются в соответствии с принципом обратной связи по измерениям длины и скорости выпуска троса. При моделировании работы системы стабилизации не учитываются запаздывание, ошибки измерений и другие возмущения, связанные с функционированием реальной системы управления.

МОДЕЛЬ ДЛЯ ПОСТРОЕНИЯ ПРОГРАММЫ РАЗВЕРТЫВНИЯ КТС

При выводе уравнений движения предполагается, что центр масс системы движется по невозмущенной эллиптической орбите и совпадает с центром масс базового КА. Трос считается нерастяжимым. При описании движения КТС

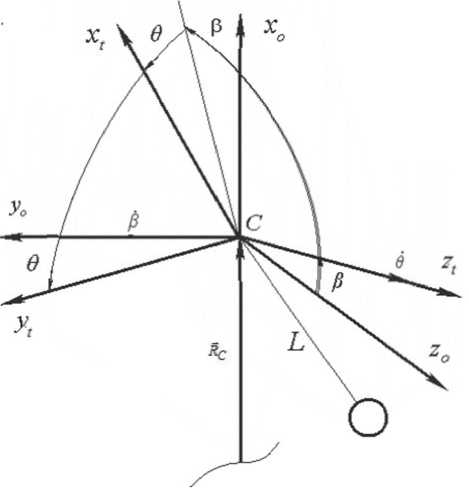
Рис. 1. Взаимное положение систем координат Cx_o y_o z_o и Cx t y t z t

используется следующие правые прямоугольные системы координат (рис. 1): 1) орбитальная подвижная система координат Cxoyozo, где C – центр масс системы, ось Cxo направлена по радиус–вектору Rc , ось Cyo – в плоскости орбиты по направлению орбитального движения; 2) система координат, связанная с тросом Cxtytzt, где ось Cxt направлена по тросу от малого КА, ось Cyt лежит в плоскости, прохо- дящей через радиус–вектор Rc и трос. Матрица перехода между системами координат Cxo yo zo и Cxt yt zt определяется стандартным образом через углы 9, в (рис. 1).

Для вывода уравнений пространственного движения КТС используются уравнения Лагран- жа второго рода d (5 T ) 5 T    5P

--c —c =-- + Q i ;

dt к ⁵ q i ) ⁵ q t      ⁵ q t

где Q x = L , q 2 = 9 , q 3 = в - обобщенные координаты, T_c и P – кинетическая и потенциальная энергии системы, L - длина троса, 9 и в - углы, определяющие положение троса относительно плоскости орбиты базового КА, Q_i – обобщенные непотенциальные силы.

Кинетическая энергия в уравнениях (1) представляет собой сумму

Т_с = 2 m ( X ² + y ² + z ² ) + T_t , (2)

где T_t – кинетическая энергия троса; x , y , z – координаты малого КА в неподвижной геоцентрической системе координат, связанной с невозмущенной эллиптической орбитой центра масс системы.

Координаты центра масс малого КА вычисляются следующим образом x = (Rc -LcosOcosP)cosu + LsinOsinu , y = (Rc -LcosOcosP)sinu -LsinOcosu, (3) z = - LcosOsinP, где u – аргумент широты.

При выводе уравнений предполагается, что параметры эллиптической орбиты за время развертывания КТС не изменяются.

Кинетическая энергия троса как любой механической системы складывается из кинетической энергии движения центра масс и кинетической энергии движения троса относительно своего центра масс ( T_r ). Поэтому

1 э

T. = L a V , ² + T ,             (4)

где V t - скорость центра масс троса, a - линейная плотность троса.

Вектор скорости центра масс троса состоит из следующих составляющих

V = V C + V S + V r ,             (5)

г д е V_c – вектор скорости центра масс системы, V_s – вектор скорости центра масс троса относительно центра масс системы за счет вращения тросовой системы координат, V_r – вектор скорости центра масс троса относительно центра масс системы, обусловленный изменением длины троса V_r = L .

Составляющие вектора V_c в неподвижной системе координат имеют вид

■

V™ = R_P cos u - Ru sin u , cx c           c

■

V cy = R c sin u + R c u cos u ,        (6)

V cz = 0 .

Компоненты вектора V_s определяются следующим образом

V sx		to sx
у sy	= D	to sy
V V sz 7		V to sz 7

L

,

где D = D T D T D T - матрица перехода от тросовой системы координат Cx_t y_t z_t к неподвижной системе координат, D u , D p , D о - матрицы элементарных вращений [16], ( T ) - знак транспонирования матрицы, to sx , to sy , to sz - проекции вектора угловой скорости вращения тросовой системы координат Cx_t y_t z_t относительно неподвижной геоцентрической системы координат (проекции определяются в системе Cx_t y_t z_t ).

Угловые скорости tosx, tosy, tosz определяются из следующих выражений to= psinO- U cosOsinp, to sy = pcosO + U sinOsinP,       (8)

to _sz = O + U cosp .

Компоненты вектора V_r в неподвижной системе координат определяются следующим об-

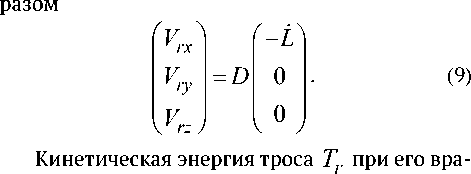
щении относительно своего центра масс опре- деляется из выражения

^Tr = I J ( to ? y ⁺ to^ z ) ,          (10)

где J_t = n L 3 /12 - момент инерции троса относительного своего центра масс.

Выражения (3–10) определяют зависимость кинетической энергии КТС от обобщенных координат и скоростей, что позволяет использовать их в уравнениях Лагранжа (1).

Для получения обобщенных сил, обусловленных гравитационным полем Земли, воспользуемся выражениями

П m = - Km / r , n t = J dn t ,      (11)

L где K – гравитационный параметр Земли, r = д/RC + L - 2LRc cos O cos p,

K p ds

JR ^ + s ² - 2 sR_c cos Ocosp

Потенциальная энергию троса запишем в виде nt=-KpL12   2 ds-----------. <12> о ^RC + s2 - 2sRc cosOcosp

Разлагая функции П_т , dn t в ряды по параметрам L , s и сохраняя члены до второго порядка включительно, получим

П_т =- Km 1 + L cosOcosp + 2 L ² ( 3cos²Ocos²p - 1 ) ,(13)

c

, _ K p ds t ~^- r

1 + s cosOcosp + 2- s ² ( 3cos² Ocos²p - 1 ) .(14)

Приближенные выражения (13–14) можно использовать, когда L / R c <<  1 и x / R c <<  1 . Вычисляя интеграл (12) с учетом (14) и дифференцируя потенциальные энергии по обобщенным координатам, получим

Q L = L ( m + L p / 2 ) v ¹ U ² ( 3cos² Ocos² p - 1 ) ,

Qo = - 2 JevVz 2cos2psin2O, (15) Qp = - 2 Je v-1U2 cos2 Osin2p, где Je = L2(m + Lp/3), v = 1 + ecos^, 9 - истинная аномалия, e – эксцентриситет орбиты, Rc = p / v - уравнение орбиты, p - параметр орбиты.

К действующим силам необходимо добавить силу натяжения T в точке выпуска троса, совершающую работу только на возможном переме-щении 5 L .

Дифференцируя кинетическую энергию (2), учитывая потенциальные силы (15) и силу натяжения троса, получим в соответствии с уравнениями Лагранжа (1) систему дифференциальных уравнений движения КТС

L = M ₁ L [ O² + (1 - v ^{- 1}) U ² + 20 U cosp -

• - U ² cos² 0 sin² p + 20 U cosp - U ² cos² 0 sin² p +

• + 20 Ui cos p - Ui ² cos² 0 sin² p + p² cos² 0 +

T + p / "²

+ и|3sinpsin20 + 3v ¹ u ² cos² Ocos² p" l---—, (16)

J m + p L

i

0 = - 2 M ₂ — (0 + u i cos p) + zi ² sin 0 cos 0 sin ² p -

• - ii cosp - 2p ² sin 20+2 z i p cos ² Osinp -

  - |-v ^{- 1}z i ² sin20cos ² p ,                         (17)

P cos² 9 = - M ₂ L (2[3 cos² 0 + U sin 20 sin P) +

+0p sin20 - U sin20 sinP - 2/10 cos²0 sinP -

- 2v ^{- 1} U ²cos²0sin2P,                         ⁽¹⁸⁾

где M i =

m + n L /2 ...    m + n L /2

--------, M 2 =-------- m + nL       m + nL / 3

Производные аргумента широты u по времени определяются известными выражениями U = -^3 ( 1 + ecos d ) u = - e sin У , (19) p ³                       p ³

,

где У = u - w _n , ® _п - аргумент перицентра.

Таким образом, в системе уравнений (17–19) имеется параметрическое периодическое возмущение, связанное с неравномерным изменением угла u . При записи уравнений (17–19) полагается R c « 0 .

ПРОГРАММА РАЗВЕРТЫВНИЯ КТС НА ЭЛЛИПТИЧЕСКОЙ ОРБИТЕ

Полученные уравнения (16–18) могут быть использованы для построения номинальной программы развертывания КТС в вертикальное положение при движении центра масс системы по эллиптической орбите. Если e = 0, то урав- нения (16–18) совпадают с аналогичными уравнениями, полученными в работе [13].

Если исходная орбита круговая, то закон развертывания КТС в вертикальное положение получен в работе [13] и имеет вид

T = ( m + n L /2 ) Q ²

• a (L - Lk ) + b ^ + 3 L

, (20)

где L_K – длина троса в конечном положении системы, a , b , c – параметры закона, Q = U = const - угловая скорость движения центра масс системы по круговой орбите.

Если программная сила натяжения троса задана в виде (20), то система (16-18) при e = 0 будет иметь асимптотически устойчивые вертикальные положения равновесия 9 = 0 и 9 = п ( 0 = L = p = P = о , L = L K ф 0 ), когда a >  3 , b >  0 [13].

Аналогичный результат можно получить и для эллиптической орбиты ( e >  0 ), если пренебречь u ‘« 0 в уравнении (17). Тогда в положении равновесия КТС L = L = 0 = 0 = P = р = 0 из уравнения (17) следует

( m + р L /2 ) LU ² ( 1 + 2v ^{- 1} ) - T = 0 . (21)

Здесь производная U определяется для эллиптической орбиты: U = Q _e v² , где Я e = VK / p ³ .

Тогда, чтобы система (16–18) имела устойчивое положение равновесия на эллиптической орбите при L = L k ф 0 , силу натяжения необходимо определять из выражения

T = ( m + р L /2 ) Q²

a ( ^{L -} L K ) ^{+ b} Q ^{+ c} ( ^У ) L

,(22)

где c(У) = v(У)3 (2 + v(У)), v (У) = 1 + e cosy.

Выражение (22) обобщает программу (20) на эллиптические орбиты, причем сила натяжения T теперь зависит от истинной аномалии У , то есть от положения центра масс системы на эллиптической орбите. Очевидно, что при у ( У ) = 1 , когда e = 0 , программа (22) совпадает с программой (20). Вертикальные положения равновесия 9 = 0 и 9 = п в плоском случае ( р = р = 0 ) будут асимптотически устойчивы при любой длине L k , если a >  c ( У ) и b >  0 . Данное утверждение доказывается с помощью стандартного метода построения линеаризованной системы относительно исследуемого положения равновесия. Причем в линеаризованной системе уравнения для переменных р,р отделяются, и их характеристическое уравнение имеет всегда чисто мнимые корни. Матрица, соответствующая остальным уравнениям линеаризованной системы, имеет при выполнении условий a >  c ( У ) , b >  0 всегда собственные значения с отрицательными действительными частями. Поэтому плоское движение КТС в этом случае при L = L k Ф 0 имеет асимптотически устойчивые заданные вертикальные положения равновесия.

Введение допущения У « 0 позволяет с одной стороны получить явное выражение для силы натяжения троса (22), а другой стороны приводит к возникновению колебаний угла 9 относительно вертикальных положений равновесия. Причем, как следует из выражений (19), эти колебания тем больше, чем больше эксцентриситет e . Однако это не приводит к колебаниям скорости выпуска троса относительно нуля, • ■ так как от переменной У правая часть уравнения (16) не зависит. Приведенные рассуждения подтверждаются также численными оценками по более сложной модели, которые приводятся ниже.

В качестве примера на рис. 2 показаны две траектории малого КА относительно базового КА (начало координат), вычисленные с использованием программы (22), учитывающей эллиптичность орбиты (e = 0.02, сплошная линия), и с использованием программы (20), заданной для круговой орбиты [13]. Не учет эллиптич- ности орбиты ведет к большим отклонениям вывода груза на вертикаль, которые при длине троса LK = 30 км достигают 1.5 км. Параметры законов a — 4, b — 3.7. Начальная высота орбиты 1000 км, масса малого КА m = 20 кг. Кроме того, не учет эллиптичности орбиты приводит к появлению отрицательных значений скорости выпуска троса (рис. 3), что для применяемых в настоящее время механизмов выпуска троса, работающих только на торможение, не допустимо. На рис.3 сплошной линией показана зависимость L (t) , вычисленная с использованием закона (22), а штриховой линией – та же зависимость, определенная в соответствии с законом (20).

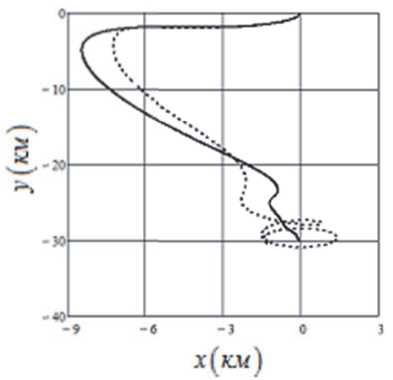
Рис. 2. Номинальные траектории движения малого КА относительно базового КА (начало координат): сплошная линия – программа (22), штриховая линия – программа (20)

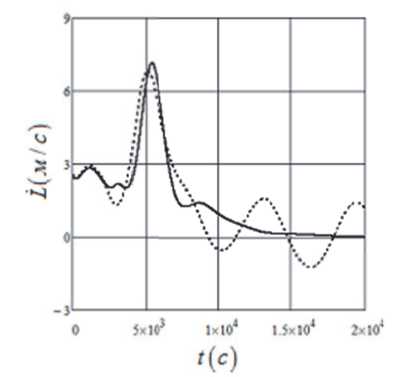
Рис. 3. Скорости выпуска троса: сплошная линия – программа (22), штриховая линия – программа (20)

Здесь надо отметить, что программы развертывания КТС в вертикальное положение часто используются в качестве составной части более сложных программ выпуска троса. Так, напри- мер, в реальном тросовом эксперименте YES2 [2] программа развертывания троса в вертикальное положение использовалась в качестве первого этапа формирования системы, причем на втором этапе применялись программы быстрого развертывания, включающие в себя участки разгона и торможения [2, 14–16]. Возникновение ошибок приведения на вертикаль на первом этапе развертывания троса из–за не учета эллиптичности орбиты неизбежно ведет к резкому возрастанию погрешностей на втором этапе, так как программы быстрого выпуска троса чувствительны к начальным отклонениям.

МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ КТС В ГЕОЦЕНТРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ

Оценка допустимости принятых упрощений и предлагаемой программы развертывания КТС на эллиптической орбите проводится по более полной модели движения, в которой трос представлялся как совокупность n материальных точек с упругими и односторонними механическими связями. Данная дискретная модель описывает движение КТС как системы с распределенными параметрами. Подобные модели обычно используются, как эталонные, для оценки применимости более простых моделей [13], [17]. Силы натяжения между точками определяются по закону Гука. Аэродинамические силы, диссипативные силы внутри троса и движение относительно центров масс концевых тел (космических аппаратов) в данном случае не учитываются. Движение происходит в центральном ньютоновском поле и описывается в неподвижной геоцентрической системе координат. При достаточно большом количестве точек n данная модель близка к математической модели с распределенными параметрами, которая представляет собой систему дифференциальных уравнений в частных производных [1].

Уравнения движения КТС записываются в виде drk        dVk

---— Vi mi ----— Gi + Ti — T , (23) dt к k d_t k k k + 1