Управление процессом буксировки танкера посредством регулирования натяжения троса

В настоящее время актуализируется проблема буксировки морского транспорта, что объясняется значительным ростом числа буксирных операций во всех районах Мирового океана. В особенности это утверждение справедливо для морских акваторий Севера Российской Федерации в связи с интенсивным освоением природных ресурсов прибрежных зон.

Следует отметить, что буксировка является одной из сложнейших операций, прежде всего с точки зрения ее безопасности, что обусловлено уникальностью обстоятельств каждой буксировки, недостаточной изученностью этого процесса и неполной обеспеченностью информацией о состоянии объектов в ходе буксировки.

Основной задачей, решаемой в процессе исследования, является оценка управляемости системы буксировки, которая включает буксир, буксируемый объект и гибкую буксирную связь между ними. Потеря устойчивости этой системы – главная причина аварий при буксировке. Одной из форм выхода подобной нелинейной системы из устойчивого состояния является возникновение автоколебаний, способы устранения которых рассматриваются в данной работе.

Материалы и методы

При исследовании процесса буксировки морских объектов наиболее сложной проблемой является возникновение автоколебаний буксируемого объекта, которые могут возникать под влиянием определенных факторов, таких как характеристики буксируемого объекта, буксира, буксирной связи; скорость буксировки; а также внешние условия – возмущения среды в виде ветра, волнения, течения и т. п. В той или иной мере указанные обстоятельства исследованы с разных точек зрения [1; 3, с. 144; 4–5]. Однако в этих исследованиях не рассматривался вопрос о регулировании процесса буксировки посредством изменения параметров самой буксирной связи: натяжения буксировочного троса и его длины. Их можно изменять, используя в качестве управляющего параметра одну из кинематических характеристик движения буксируемого объекта: угол θ отклонения троса от ДП буксируемого судна, угловую скорость ω его поворота или угол дрейфа β. Эффективным способом изучения такого управляемого процесса является компьютерное моделирование; построение математической модели судна представлено в работе [2, с. 141]. Дальнейшая работа по моделированию проведена в рамках вычислительной среды MathCad; выбраны три дифференциальных уравнения движения буксируемого судна [1], они дополнены дифференциальным уравнением кинематического характера для движения буксирного троса, рассматриваемого как стержень. Коэффициенты аkj правых частей дифференциальных уравнений вычислены в соответствии с моделью, выполненной для танкера проекта 214 RN "Архангельск" (в балласте) как более склонного к автоколебаниям. Система решается с помощью встроенной функции интегрирования rkfixed() с фиксированным шагом. При интегрировании использовались следующие исходные данные1:

– параметры судна и его математической модели:

Fdp = 947 L = 162 V = 24 912 Iz = 39101 650

k11 = 0.034 k 22 = 0.455 k 66 = 0.453

m11 = p-V• (1 + k11) m22 = p-V• (1 + k 22) Izz = Iz ■ (1 + k 66)          L

Cmm = 0.042 Cmm = 0.076 CyP = 0.332 C 2 y = 0.286 Cy® = 0.061 Np = 0.5pv ² F _dp

– характеристики руля танкера:

Ar = 27.4 Ir = 80 Cyra = 2.4 x = 0.3 1 Nr = 0.5 -p- v ² - Ar fr = Cyra -x- Nr ;

– коэффициенты дифференциальных уравнений а jk :

NpCmavL + frlr2       NpCm^L - frlr          T()xTL all =------------------ a12 =----------------- a13(9) =-------- v • Izz                          Izz                        Izz

O1 mllv - frlr / v      nn Np             T (9)            fr a21 =------------ a22 =----- a23(9) =----- a222 =----- vm22            vm22         vm22        vm22

a31 = 1 + xT/( -)     a3'2 = v a34 = v

L              l l

– параметры буксирного троса и закон изменения его натяжения в зависимости от угла θ отклонения направления троса от диаметральной плоскости танкера, которое в значительной мере определяет степень рыскания танкера при буксировке, поэтому выбрано в качестве задающего параметра движения в законе управления процессом буксировки:

xT = 0.5 1 = 2 ■ L k9 = 200 T 0 = 100

T (9) = T 0 + к 9^9^ sign(9)

Детали задания коэффициентов уравнений и решения приведены в виде формул (1)–(3). Все величины имеют размерности Международной системы единиц (СИ), кроме водоизмещения судна V, приводимого традиционно в тоннах.

Результаты и обсуждение

Пропорциональный закон управления натяжением

В процессе исследований [3], а также на основании морской практики установлено, что увеличение натяжения троса уменьшает рыскание буксируемого судна. Закон регулирования выглядит как просто пропорциональный:

T (9) = T 0 + k 9^ sign(9) ,

где ТО - некоторое постоянное значение натяжения; k9 - коэффициент усиления, функция знака sign(9) добавлена для двусторонней реакции натяжения на угол отклонения θ, уменьшая или увеличивая натяжение в соответствующих случаях. Следует отметить, что при использовании закона управления натяжением троса (5) часть коэффициентов дифференциальных уравнений движения системы, которые зависят от регулируемого параметра, перестают быть константами; в данном случае это утверждение относится к коэффициентам а31 и а23, они становятся функциями угла θ.

Следует решить систему дифференциальных уравнений, представленную в виде группы формул:

ф1 = ш ш1 = -а11-ш + a12 -р - a13(9) ■ sin(9)

Р1(ш, Р, 9) = a 21 -ш - a 22 ■ ( Cy P + C 2 y ■ y ■ |sin(P)|) sin(P) - a 222 ■ sin(P) - a 23(9) ■ sin(9) 91(ш, P, ф) = a 13 ■ш- a 32 ф + a 34 ■ф

Решение системы уравнений (6) производится с помощью встроенной функции rkfixed() среды MathCad. Они записаны для наших кинематических переменных в следующем порядке: курс судна ф, угловая скорость поворота ю, угол дрейфа Р, угол отклонения троса 0. Цифрой 1 обозначены первые производные соответствующих параметров (ф1 — первая производная по времени от курса и т. д.). В синтаксисе MathCad эти переменные становятся компонентами вектора-столбца y, который в транспонированном виде выглядит так: у Т = ( у ₀ , у 1 , у 2 , у ₃ ) . Заданы начальные значения переменных; в качестве начального возмущения определена угловая скорость поворота 0.05 = 2.865 °/с. Число шагов интегрирования выбрано равным 3000 (шаг равен одной секунде). Вектор производных задан вектором D(t, y), в котором компоненты представлены функциями вектора переменных y. Обращение к функции интегрирования Рунге – Кутты Z = rkfixed(y, 0, m, m, D) выполняет процедуру решения системы дифференциальных уравнений. Результаты решения размещаются в матрице Z, которая в данном случае состоит из пяти столбцов и 3001 строки. Первый столбец матрицы содержит текущее время интегрирования, остальные столбцы – кинематические переменные в указанном выше порядке. Эти этапы решения представлены следующей группой формул:

m = 3000 n = 0.m

f 0 1		f У          1
0.05	D ( t , y) =	"И У 1 , У 2 , У з )
0		P1( У 1 , У 2 , У з )
10 J		,91( У 1 , У 2 , У о ) ,

Z = rkfixed( y, 0, m, m, D)

K0 = Z , coO = Z , B0 = Z , 00 = Z , n n,1 n n,2 M vn n,3 v vn n,4

Ряд формул группы (7), расположенных в четвертой строке, из решения (матрицы Z) извлекает столбцы 1-5 с помощью присвоений их векторам с обозначениями наших переменных. Так, формула ю0 _п = Z n ₂ означает запись третьего (счет с нуля) столбца матрицы Z в вектор ю0. Каждый элемент записывается с индексом n. После этого появляется возможность строить графики изменения основных кинематических характеристик, полученных в процессе такого моделирования буксировки танкера. На рис. 1 приведены графики изменения угловой скорости поворота ю0, угла дрейфа Р0 и угла отклонения троса 00 от ДП. Процесс автоколебаний не возникает ни по одной из этих характеристик, существенное начальное возмущение (~3 °/с) затухает, однако этот процесс затягивается (примерно до 2500 с). Данное регулирование натяжения представляется действенным и имеющим право на обсуждение с технической точки зрения.

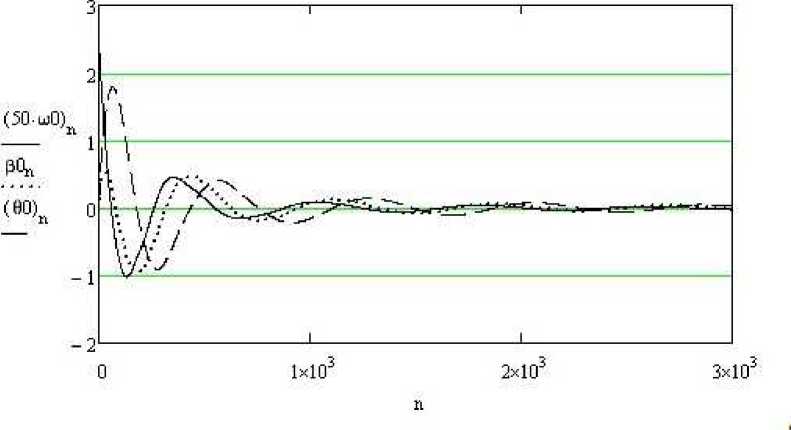
Рис. 1. Графики изменения кинематических характеристик, полученных в результате интегрирования (Т = 100 кН, к0 = 0) Fig. 1. The graphs of changes in kinematic characteristics obtained as a result of integration (Т = 100 кN, k0 = 0)

Возможные возражения о том, что процесс автоколебаний не возникнет и при отсутствии предлагаемого регулирования, опровергаются решением системы уравнений при нулевом коэффициенте усиления kθ = 0. Так, на рис. 2 показан характер изменения кинематических параметров движения в этом случае. Из графиков видно, что в системе возникают незатухающие колебания, более того, угол отклонения троса θ0 (пунктирная линия) резко растет и выходит за пределы графического поля с выбранным масштабом изображения.

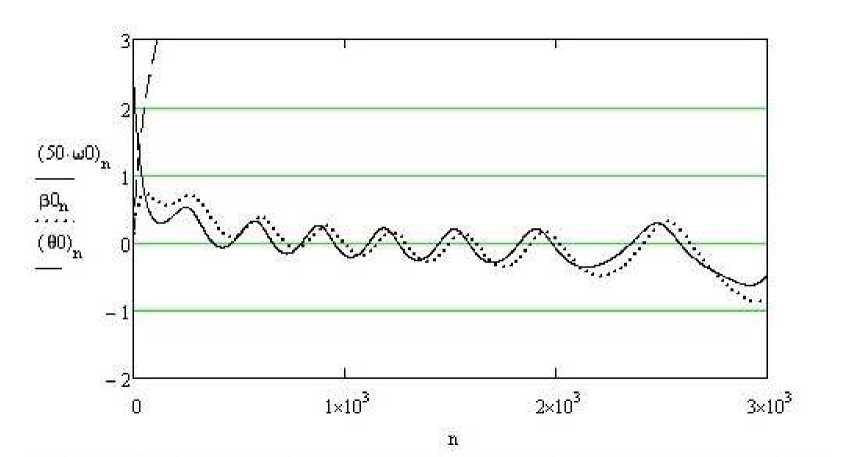
Рис. 2. Результаты интегрирования системы уравнений при отсутствии регулирования натяжения буксирного троса (Т0 = 100 кН, kθ = 0) Fig. 2. The results of integrating the system of equations in the absence of regulation of the towing cable tension (Т0 = 100 кN, kθ = 0)

Фазовый портрет на плоскости "угол отклонения θ0 - скорость угла отклонения θs" показан на рис. 3. Данный график демонстрирует развивающийся процесс автоколебаний. Для сравнения: на рис. 4 приведен фазовый портрет в той же фазовой плоскости, когда натяжение троса регулировалось с коэффициентом усиления kθ = 200, где отражена сходимость процесса к стационарной точке (0, 0).

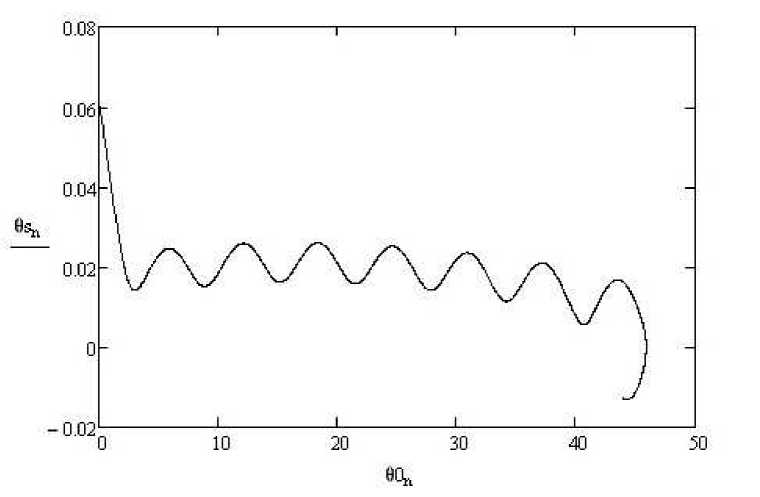
Рис. 3. Фазовый портрет на плоскости "угол отклонения θ0 – скорость угла отклонения θs" при отсутствии регулирования натяжения троса (kθ = 0)

Fig. 3. The phase portrait on the plane "deflection angle θ0 – velocity of deflection angle θs" in the absence of cable tension regulation (kθ = 0)

Чтобы оценить количественно качество такого регулирования, введен показатель качества. Для этого выбрана средняя квадратическая характеристика отклонения угла θ для m точек интегрирования:

Z ceo„ )2Q1 = \ ---------.                                              (8)

m

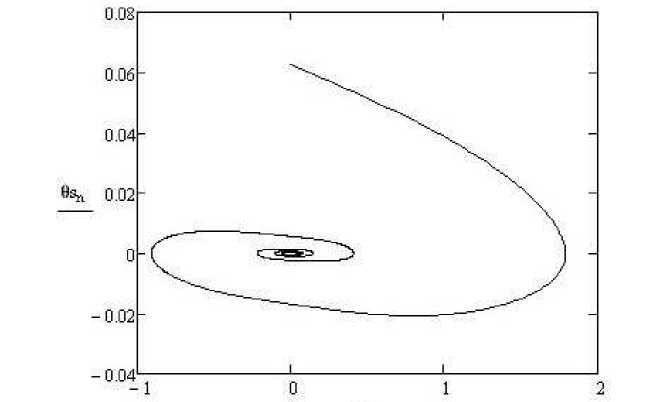
Рис. 4. Фазовый портрет на плоскости "угол отклонения троса θ0 – скорость угла отклонения θs" при регулировании натяжения троса (kθ = 200)

Fig. 4. The phase portrait on the plane "angle of deflection of the cable θ0 – speed angle θs" when adjusting the cable tension (kθ = 200)

Изменяя коэффициент усиления kθ и фиксируя показатель качества регулирования Q1, можно подобрать оптимальный коэффициент усиления в законе управления (5). Так, для нашего случая имеем следующие пары (kθ, Q1): (100; 0.55), (200; 0.373) и (300; 0.303). Формально показатель Q1 убывает (качество растет) с увеличением коэффициента усиления, но в начальные моменты процесса начинают расти значения натяжения, определяемые законом управления. Следовательно, для сохранения целостности буксировочного троса следует остановиться на том значении kθ, при котором натяжение не превышает допустимые значения.

График изменения натяжения троса в зависимости от времени приведен на рис. 5. Коэффициент регулирования равен 200, а максимальное натяжение не превышает 500 кН.

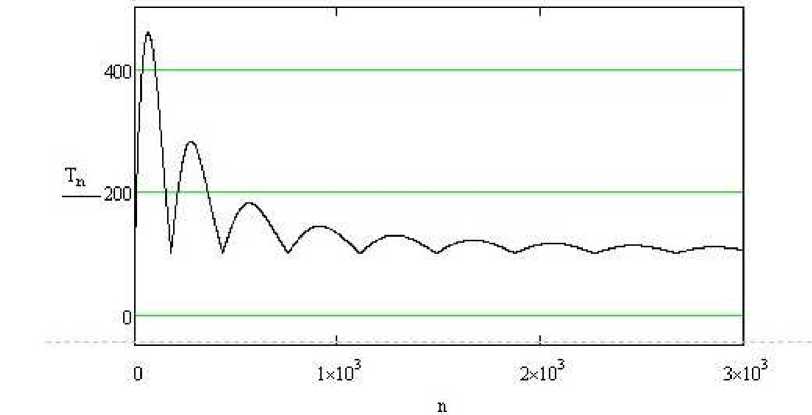
Рис. 5. Изменение натяжения троса в процессе его регулирования (Т0 = 200 кН, kθ = 200, показатель качества регулирования Q1 = 0.373) Fig. 5. Changing the tension of the cable during its regulation (T0 = 200 kN, kθ = 200, quality control indicator Q1 = 0.373)

Для продолжения дальнейшего исследования в этом направлении можно ввести комплексный показатель качества Q2, в который также входит значение натяжения троса:

Q2

у [р1<ео „ ) 2 +Р2( Т n ) ² ] n

m

При использовании указанного показателя также возникают проблемы, требующие отдельного изучения. Одной из них является выбор весовых коэффициентов ρ1 и ρ2, которые определяют долю каждого показателя (угла отклонения θ или натяжения троса Т) в общем показателе качества Q2. Минимизируя этот показатель качества управления, можно одновременно добиться малых отклонений троса и допустимых нагрузок на буксировочный трос.

Пропорционально-дифференциальный закон управления натяжением

Для решения проблемы улучшения показателей регулирования каким-то иным способом, а не только за счет увеличения коэффициента усиления в законе (5), логично обратиться к обычной практике и усложнить закон управления, например, введя в него производную θs угла отклонения троса θ. Тогда закон управления (5) примет следующий вид:

T (9) = T 0 + к 9-9- sign(9) + k9s -9 s ■ sign(9 s ).                             (10)

Реализация закона (10) в рамках интегрирования системы дифференциальных уравнений с помощью средств MathCad требует особой подготовки. Дело в том, что в уравнениях группы (6) нет переменных (производных), а включены только производные в виде функций в левых частях дифференциальных уравнений. Поэтому для реализации управления (10) средствами MathCad следует усложнить систему уравнений, введя в нее три уравнения и три переменные (производные): ωs = dω/dt, βs = dβ/dt и θs = dθ/dt. Вводить производную курса не следует, так как его производная есть угловая скорость поворота. Данные преобразования представлены тремя группами формул:

T (9, 9s) = T 0 + к 9-9- sign(9) + к 9 s ■ 9 s ■ sign(9s) Ts(9, 9 s ) = к 9-9s ■ sign(9)

^l(to) = to to1(to, p, 9,9s) = -all -to + a12 - p - T^^xTL sin(9)

Izz p1(to, p, 9,9s) = a21 -to - a22(Cyp + C2y - у Isin(p0)| -) sin(P) - a222 sin(P) - T(9,9s) sin(9) m22 - v

91(to, P, ф) = a 13 -to- a 32 -p + a 34 -ф

_     _ _ .                      _    T (9,9s)xT■ L             Ts(9,9s)xT■ L .

m2(m, 9, ю s, Ps, 9s) = -al 1 ■ms + al2 ■Ps--cos(9)9s--sin(9)

Izz                       Izz

92(ms, Ps, m) = a13 ■ms - a32 ■Ps + a34 ■m

TT (p, ps, 9,9s) = T^^sl cos(9)9s + T^^i^s) sln(9) + a222 cos(p)ps m22 ■ v            m22 ■ v p2(m, p,9, ms, ps, 9s) = a21 ■ms - a22 ■ (Cyp + C2y ■y |sln(p0)| ■)cos(p)ps - TT(p,ps, 9,9s)

	Г 0 )		Гф 1( y ) 1                     '
	0.05		® 1( У 1 , У 2 , У з , У 4 )
	0		Р 1( У 1 , У 2 , У з , У 4 )
y =	0	D ( t , У ) =	9 1( У 1 , У 2 , У о )	.                                 (14)
	0		® 2( У 1 , У з , У 4 , У 5 , У б )
	0		P 2( У 1 , У 2 , У з , У 4 , У 5 , У б )
	1 0 J		ч9 2( У 4 , У 5 , У 1 )            ,

В указанных формулах вторые производные от кинематических характеристик обозначены цифрой 2: ω2 – вторая производная угловой скорости; β2 – угла дрейфа; θ2 – угла отклонения троса. Их выражения получены простым дифференцированием по времени правых частей первых производных ω1, β1 и θ1. В формулах (11) показан сам закон управления (10) и производная от T(θ) в виде функции Ts(θ, θs) = kθ · θs · sign(θ), которая входит в пятое и седьмое уравнения новой дифференциальной системы. Уравнения (12) задают первые производные параметров, а формулы группы (13) – вторые производные. Начальный вектор переменных y и вектор правых частей системы D(y, t) получили размерность, равную семи, и в D(t, y) стали входить переменные y 0 –y 6 . В формулах группы (14) приведены начальное значение вектора y и вектор D(t, y). Начальное возмущение по угловой скорости поворота сохранено на уровне 0.05 с ^–1 .

После формирования новой системы дифференциальных уравнений обращаемся к той же функции интегрирования rkfixed() и получаем решение в виде матрицы Z:

Z = rkfixed(y, 0, m, m, D).

Из матрицы Z выделяем семь кинематических параметров буксировки:

K 0 = Z ^(1> , m0 = Z< ^2> , p0 = Z^{( 3} , 00 = Z^{( 4} , m0s = Z^{( 5>} , p0s = Z ⁶ , 90s = Z 7^.                (15)

В отличие от подобной операции в формуле (7) здесь использована другая нотация столбца в виде его номера, показанного верхним индексом в косых скобках.

При этом коэффициенты усиления по углу отклонения θ и его производной θs взяты равными kθ = 50, kθs = 60. Они были выбраны (посредством перебора вариантов) как наиболее эффективные для управления, что подтверждает графическая часть решения (рис. 6). Из графиков видно, что угол дрейфа и угловая скорость поворота возвращаются к начальным нулевым значениям примерно за 1 000 с, а угол отклонения троса θ примерно за 800 с приходит к новому стационарному значению, т. е. танкер движется параллельно буксиру с постоянным смещением в боковом к траектории буксировки направлении. Данная ситуация знакома специалистам по буксировке морского транспорта.

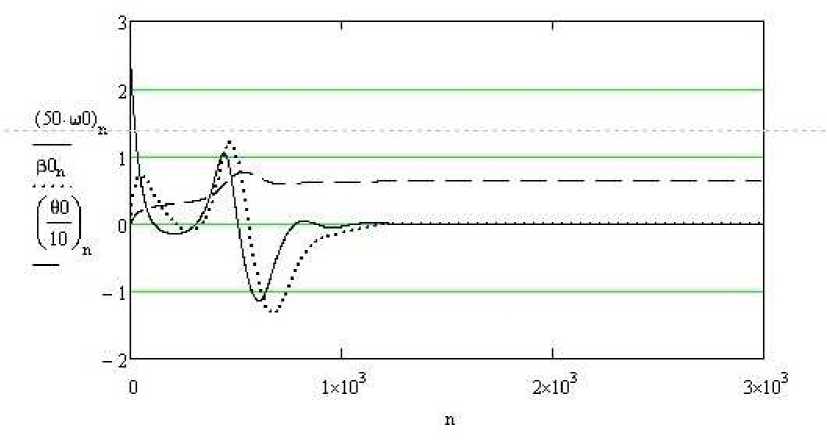
Рис. 6. Результаты интегрирования системы дифференциальных уравнений, полученные при использовании пропорционально-дифференциального закона регулировании натяжения троса (Т0 = 100 кН, kθ = 50, kθs = 60)

Fig. 6. The results of integrating the system of differential equations obtained by using the proportional-differential law of cable tension control (T0 = 100 kN, kθ = 50, kθs = 60)

Графики изменения регулируемого натяжения троса и скорости изменения угла отклонения троса, представленной в законе регулирования (10), изображены на рис. 7. Верхние графики отражают изменение постоянного регулируемого натяжения Т0, представляющего собой сумму двух переменных составляющих этого натяжения: одна из них формируется с помощью угла отклонения θ, другая – с помощью скорости изменения этого угла θs. Поэтому на рис. 7 (верхние графики) показаны три кривые (одна отражает натяжение троса, две других – указанные составляющие). После возникновения возмущения (в первые моменты движения буксировочной системы) значительную роль в регулировании натяжения играет именно третья составляющая закона (10), определяемая скоростью изменения угла отклонения θs. Характер ее изменения представлен на рис. 7 (нижний график).

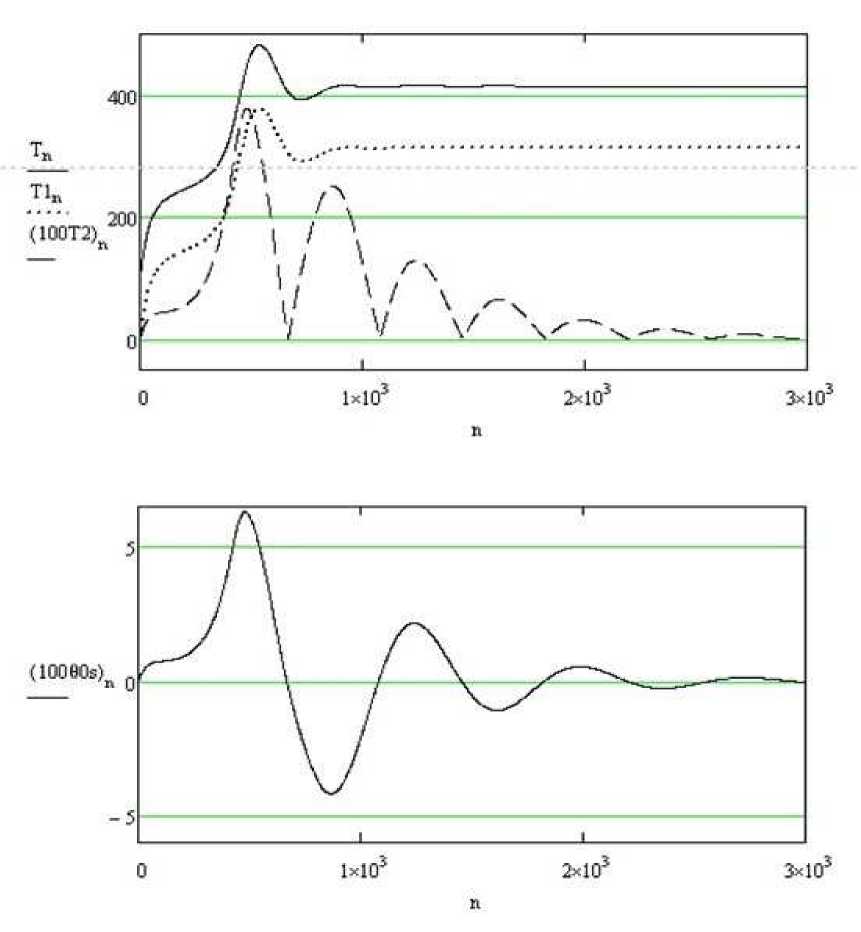
Рис. 7. Изменение во времени регулируемого натяжения троса Т и двух его составляющих Т1 и Т2 (верхние графики) и скорость θs изменения угла отклонения троса, используемая в законе регулирования (нижний график) Fig. 7. The time variation of the adjustable tension cable T and its two compounds Т1 and T2 (top) and the speed θs of changing the cable deflection angle used in the law of regulation (bottom)

Таким образом, влияние увеличения натяжения буксирного троса на характер движения буксируемого судна в достаточной степени изучено; созданы различные буксировочные лебедки, реализующие этот эффект. В настоящее время возникла необходимость моделирования указанного эффекта, в ходе которого уточняется действие фактора натяжения троса и устанавливаются параметры движения буксировочной системы, определяющие качество этого процесса (например, координата точки крепления троса xT). Решение дифференциальных уравнений движения с введением в них законов управления натяжением троса способствует изучению влияния натяжения с разных точек зрения, определению направления дальнейших исследований процессов буксировки, не самых простых в морской практике. В среде MathCad оказалось возможным нарастить систему дифференциальных уравнений движения с четырех уравнений (7) до семи (14), что позволило ввести в решения не только пропорциональный закон управления натяжением троса (5), но и пропорциональнодифференциальный закон (10), и сравнить их по эффективности. При решении проблемы с использованием закона (10) с учетом определенного сочетания коэффициентов усиления по углу отклонения и его скорости появляется интересный эффект быстрого затухания автоколебаний, возникающих в результате начального возмущения по угловой скорости поворота; при этом угол отклонения троса получает новое (скачкообразно изменившееся) установившееся значение.

Выводы

Проведенные исследования и представленные результаты в численной и графической формах свидетельствуют о том, что введение в процесс моделирования буксировки законов управления натяжением троса по углу отклонения троса от ДП танкера дает безусловный эффект, не позволяя танкеру перейти в стадию автоколебательных движений. Это утверждение, естественно, относится к тем случаям, когда отсутствие подобного управления ведет не только к переходу в автоколебания, но и их развитию.

Сравнение законов управления только по углу отклонения троса (5) и с включением в него скорости изменения такого угла (10) не выявляет особых преимуществ последнего. Меры по усложнению закона управления не окупаются практическим эффектом, хотя и приводят к интересным результатам, которые требуют дальнейших исследований.

Кроме законов управления (5) и (10), можно, в принципе, использовать аналогичные законы, применяя в качестве формирующего сигнала для управления угловую скорость поворота ω или угол дрейфа β (а не угол отклонения троса θ). Такие исследования ведутся на кафедре судовождения Мурманского государственного технического университета.